基于高斯过程混合模型的大气温湿度预测

周亚同，赵翔宇，何 峰，石超君

（河北工业大学电子信息工程学院，天津市电子材料与器件重点实验室，天津 300401）

0 引 言

温湿度预测在国民经济各领域有重要作用。研究可分为室内温湿度预测和室外温湿度预测。室内植物生长很大程度依赖于温度和湿度，为使植物健康生长减少经济损失，实现温湿度智能控制显得尤为重要[1-2]。对于室外温湿度预测，是气象学领域重要的参数指标，同时为其他应用领域提供气象保障[3]，例如道路、航空与固体表面监控等领域中，主要目的为保障行人安全与科研顺利进行[4-5]。近年来，针对温湿度预测已提出一些预测模型并取得一定进展，但总体上来看预测效果仍有较大提升空间[6]。

对于室内温湿度预测：王定成等[7-9]基于支持向量机（support vector machine, SVM）回归模型实现温室环境温度预测。左志宇等[10]提出一种时间分析法，采用自回归滑动平均（auto regressive and moving average, ARMA）模型进行温度单步预测。邹伟东等[11-14]基于人工神经网络（artificial neural networks, ANN）预测温室中温湿度。吴曼玲等[15]利用灰色模型预测温室内温度，以便对地源热泵循环泵进行变频调控。

对于室外温湿度预测：张丽丽等[16-18]主要采用 ANN预测固体表面、航空发动机及路面表面温度。于广滨等[19-20]将 SVM 应用于航空发动机与绕组表面温度预测中。Nuijten对机场路面温度预测建立物理模型[21]，将飞机对路面影响等因素考虑进去，实现提前3个小时温度预测。

但上述预测模型均存在一些不足，例如ARMA和灰度模型预测准确率较低；ANN预测比较复杂，易发生过拟合或陷入极小值点；SVM及一些物理预测模型并非概率模型，无法输出置信区间，降低了预测结果可靠度等。高斯过程（gaussian process, GP）模型由于其兼具ANN和SVM等传统模型的优点，已应用于时间序列预测[22-24]。但是单个 GP模型很难反映温湿度序列在不同时段间的细微差异。高斯过程混合（gaussian process mixture, GPM）模型[25]，采用“分而治之”策略，将样本分为若干组，对每个样本组分配一个GP模型进行预测，细致描述不同时段间的细微差异。例如对于温度序列而言，同一天的早晚温度要明显低于午间温度，而相邻几天的早、中、晚各自温度规律又有一定相似性，因此将早、中、晚的温度序列划分为3个模态，用3个GP的混合模型（GPM）预测，结果优于用单个GP预测。

GPM模型目前仍在不断发展，其学习算法中期望最大算法（expectation maximization, EM）最为常用。EM在学习过程中常引入近似策略，但近似策略的选择直接影响到最终预测结果。因此本文根据 EM 提出一种基于隐变量后验硬划分迭代学习的高斯过程混合模型，并将之用于温湿度多模态预测。此模型在 EM 学习算法基础上，采用隐变量后验硬划分方式迭代学习，不仅学习速度快，而且能进行温湿度序列的多模态预测。由于GPM为无环境因子输入模型，因此本研究不仅对大气中温湿度预测有促进作用，同时对温室中温湿度预测具有一定借鉴价值。

1 高斯过程混合模型的原理

1.1 GP模型原理简介

在回归预测中，设待求的预测函数为 f （ x）。GP模型假设 f （ x）是一个高斯过程，具体表达式见公式（1）。

其中 m（ x）为高斯过程的均值函数，k（ x, x ′）为高斯过程的协方差函数。在回归预测问题中，采集的序列通常含有高斯白噪声。假设期望为0、方差为的高斯白噪声e( x)如公式（2）。

若考虑上述噪声，则含噪序列 g （ x）的表达式见公式（3）。

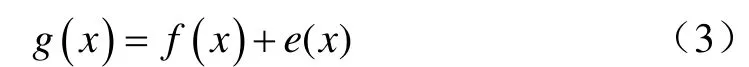
综合（1）至（3）式可知 g （ x）仍为一个高斯过程[26]，其表达式见公式（4）。

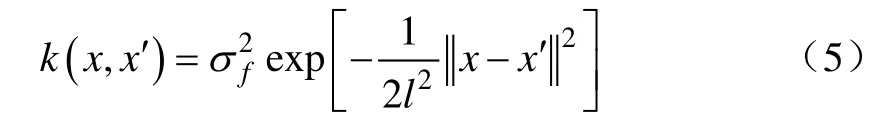
GP模型解决回归预测问题时，需先求出条件概率分布 P （ gt+1|gt），然后取其均值为样本 xt+1处的最终预测值。条件概率分布表达式见公式（6）。

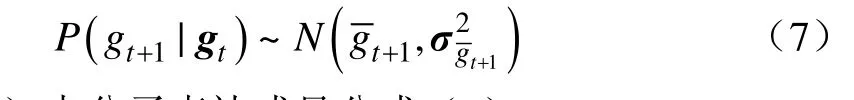
现设式（6）中分子表达式见公式（8）。将上式中矩阵1t+C 分块为，其中tC表示1t+C 中除去最后一行及最后一列的剩余部分，κ为1t+C 中右下角最后一个数值，Tk为1t+C 中最后一行除去κ的行向量，k为1t+C 中最后一列除去κ的列向量。因此获取1t+C 的逆为因此最终条件概率分将其作为样本

1.2 GPM模型的基本原理

GPM是一种典型的混合模型，其中每个组分都是一个GP分量。一般用tz c= 表示第t个样本属于第c个GP分量，并分别用cX和cy表示第c个GP分量的输入矩阵和输出向量。因此GPM模型可表示为式（9）~（10）[29]。

本文GPM模型首先采用如下多项分布门限函数生成隐变量tz。

其中πct为样本所属分量的比例系数，然后令每一个样本的比例系数都一致，即 πct=πc，则πc为混合比例系数。对于此GPM模型，设整体隐参数为输入矩阵和输出向量分别为X和y，二者满足以下分布关系[30]。

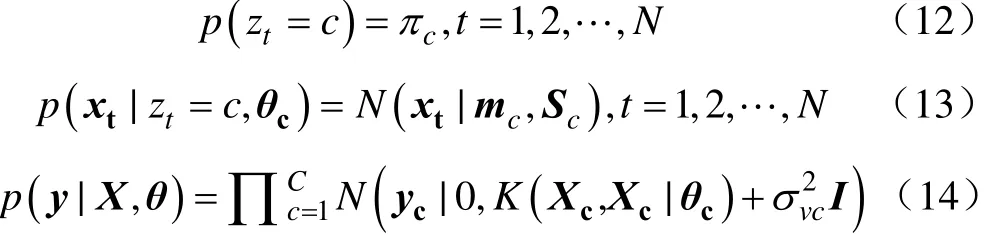
上式中cm 为第c个GP分量的均值，cS为第c个GP分量的协方差，tx为输入矩阵中的第t个向量，K为上节中k的矩阵形式。式（13）服从高斯分布，式（14）由式（9）和式（10）结合而成。第c个 GP分量的待定参数为为上节中平方指数协方差函数在第c个 GP分量的参数。因此为GPM模型待估计的所有参数。对于此GPM模型，由于各GP分量的均值 mc不同，使得每个分量能集中描述不同的时间序列输入区域，因此GPM模型可用于刻画时间序列的多模态特性。

2 GPM模型的隐变量后验硬划分迭代学习算法

本文提出的隐变量后验硬划分迭代学习算法，与GPM模型传统的MCMC、VB或者EM学习算法相比，采用了采样近似策略，在 E步中根据最大后验概率准则分配学习样本，在M步通过最大似然法估计各GP分量的待定参数，从而大幅减少算法的计算复杂度。算法的具体实现步骤如下。

第二步（M步）：参与混合的各GP分量基于最大似然估计独立学习，其中混合比例系数cπ以及输入分布的均值cm 与协方差阵cS分别用如式（15）解析式求解。

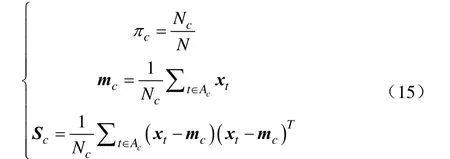
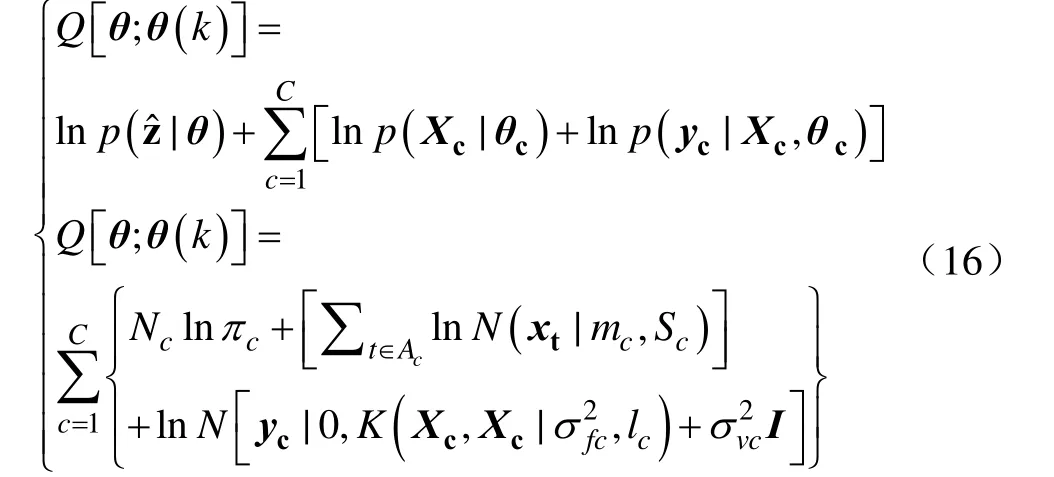
第三步（E步）：根据最大后验概率准则对学习样本重新指定组别，其中ˆtz为分组结果，等同与上节的tz。

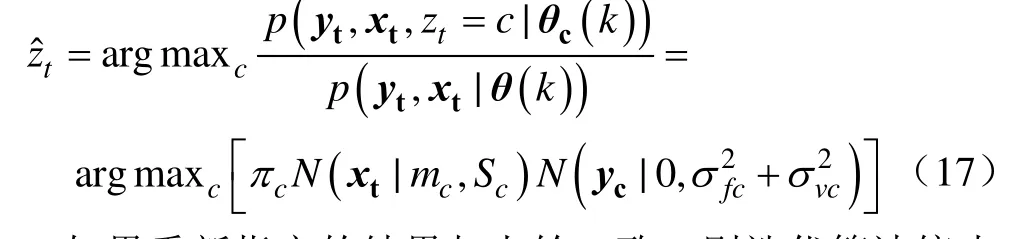
如果重新指定的结果与上轮一致，则迭代算法停止并输出最终结果；否则返回第二步。

其中z c*= 表示测试样本属于第c个GP分量。然后将测试样本分配到第z组，再由单个GP分量的预测式可得预测分布。该预测式中所需学习样本为最后一次迭代时被分配到第z组的学习样本。

3 温湿度时间序列解析

3.1 温湿度序列来源

温湿度时间序列来源于 UCI dataset数据库（http://archive.ics.uci.edu/ml/datasets.html）。序列通过一个金属氧化物化学传感器实时采集，分别记录试验地区大气中温度和湿度的分时响应。数据库中储存了从2004年3月11日0点到2015年4月3日23点，共389 d×24 h=9 336个样点。试验选取其中42 d×24 h=1 008个样点作为温湿度序列进行预测。为尽量避开空值点，湿度取值范围：2004年6月10日0点到2004年7月21日23点。温度取值范围：2004年6月15日0点至2004年7月26日23点。由于序列为真实采集，难免存在空值点与奇异值点。对于个别空缺样点补全处理，采用均值补偿法，利用相邻的 2个样点求平均值来代替；对于连续空缺样点补全处理，采用经验修正法，通过长期积累的经验对样点进行填充；对于个别奇异值矫正，采用阶段性阈值过滤法，根据不同时间段，人为根据经验设置不同偏差阈值，若某一时刻偏差超过此阈值，则将此时刻样点过滤掉，变为零值，再利用空缺样点的处理方法处理此点；对于连续奇异值矫正，采取曲线置换法，通过寻找相同时间段的负荷曲线来替代当前异常曲线，并将补全接头处进行平滑处理[31]。在特性分析与预测之前，将序列做归一化处理，采用处理方式为离差标准化。原始序列经过离差标准化处理后，变量区间会落在（0,1）上，可以很大程度上消除量纲影响，并减小变异因素对实际效果造成误差。归一化后的温度和湿度序列如图1所示。

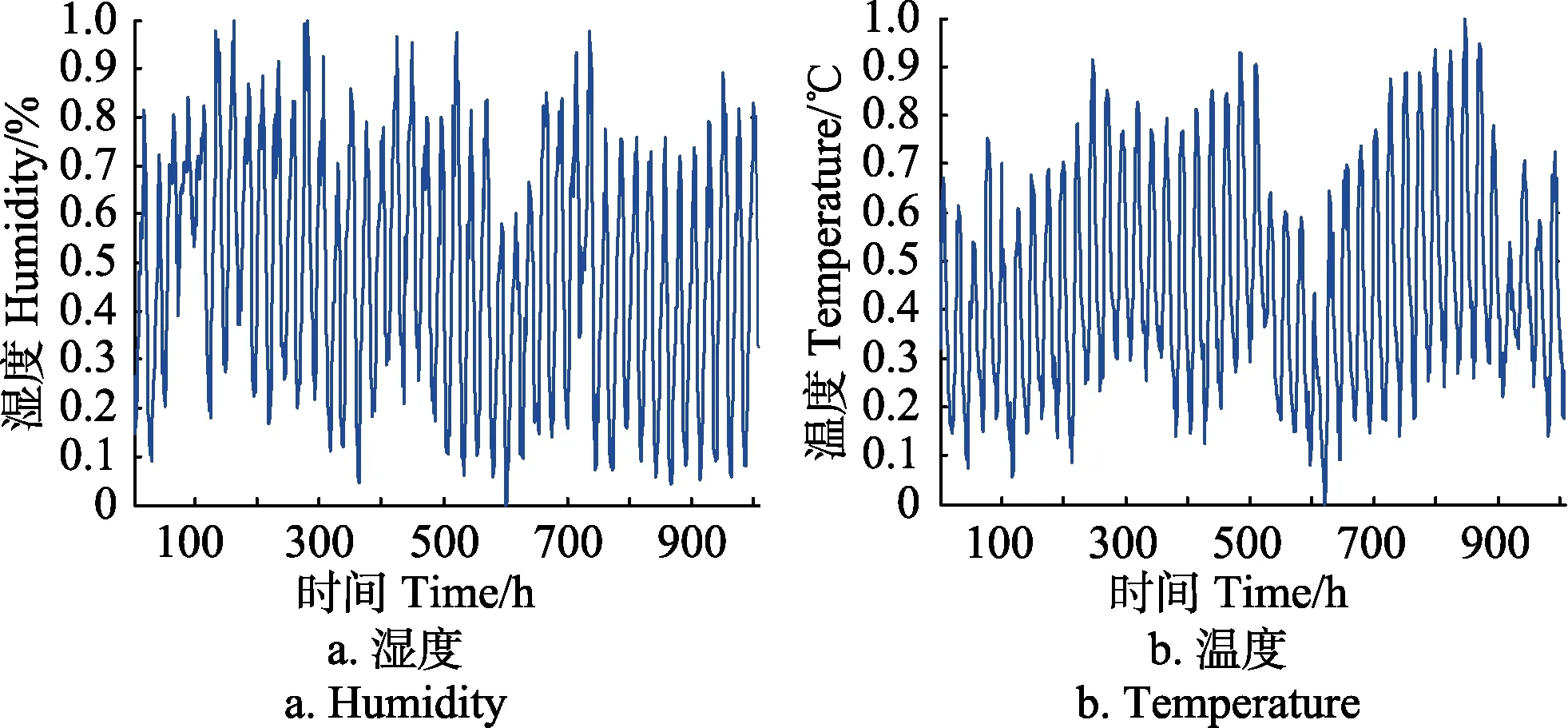
图1 温湿度归一化序列Fig.1 Normalized sequence of temperature and humidity

3.2 温湿度序列的预测特性分析

下面从自相关函数、偏自相关函数、最大 lyapunov指数、预测递归图与饱和关联维数等 5个方面入手，深入解析温湿度序列的预测特性。

1）自相关函数。自相关函数作为判定时间序列是否为线性的直接标准，详细描述了序列某时刻与另一时刻的依赖关系。通过设定固定时延参数，可以得出在时延范围内，初始时刻与任一时刻的关联程度。现对温湿度序列求自相关函数，时延最大为200，其结果如图2所示。图中序列的自相关函数从第 7个时延开始，数值已降为负，说明温湿度序列具有较强的非线性特性。

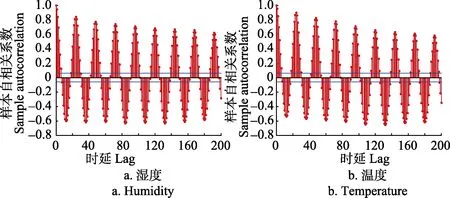
图2 温湿度序列自相关函数Fig.2 Autocorrelation function of temperature and humidity

2）偏自相关函数。时间序列的平稳特性是其预测性的重要指标，而偏自相关函数很好揭示时间序列的平稳性。现对温湿度序列求偏自相关函数，时延最大为100，其结果如图3所示。从图中看出，在t+1 (原点为t时刻)时刻处有单个较大的峰值，t+3时刻后的值大多收敛于置信区间内，证明所选温湿度序列是非平稳的。

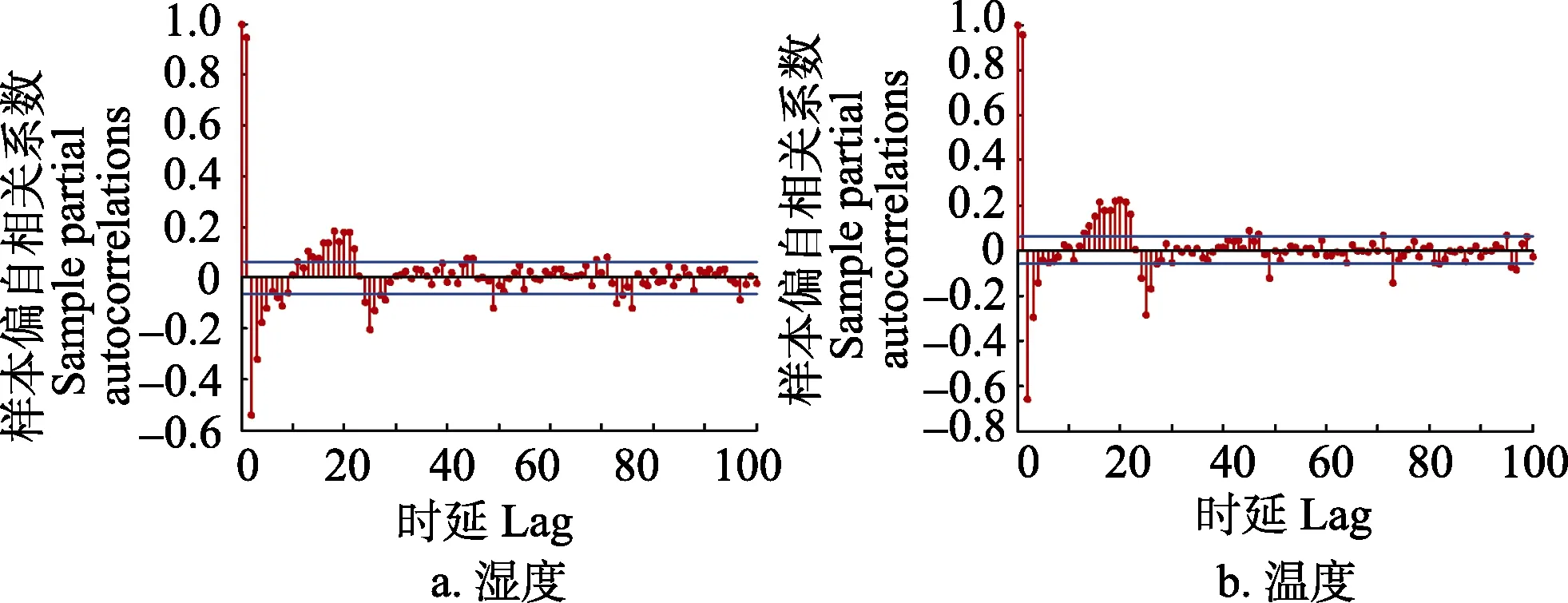
图3 温湿度序列偏自相关函数Fig.3 Partial autocorrelation function of temperature and humidity

3）最大Lyapunov指数。Lyapunov指数能很好反映时间序列的混沌特性。当序列的最大Lyapunov指数小于零时，此序列具有稳定的不动点；当最大Lyapunov指数等于零时，此序列具有周期解；当最大Lyapunov指数大于零时，此序列具有混沌特性。本文利用Wolf法循环求得20个周期下温湿度序列的最大Lyapunov指数。其中每个周期为24h，即1d。其结果如图4所示。从图中看出，序列的最大Lyapunov指数均大于零，证明其皆有一定混沌特性。

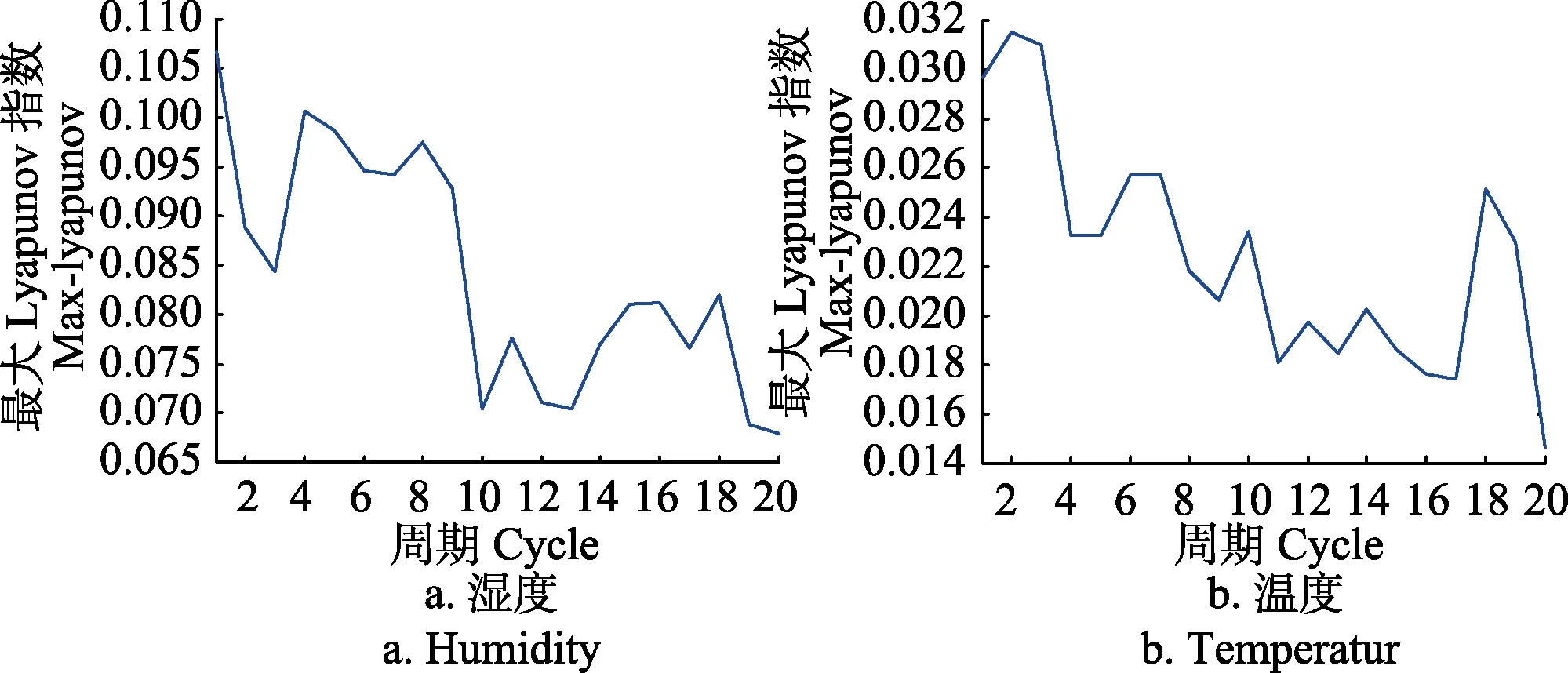
图4 温湿度序列最大Lyapunov指数Fig.4 Maximum Lyapunov exponent of temperature and humidity

4）饱和关联维数。根据关联维可以区分时间序列是否具有随机特性或混沌特性。当关联维数逐渐增大但不饱和时，此序列具有随机特性，反之具有混沌特性。现对温湿度序列求关联维数，嵌入维数d分别从2取到8，其结果如图 5所示。从图中看出，序列的关联维数皆随着嵌入维数的增大达到饱和，因此再次验证温湿度序列具有一定混沌特性。

图5 温湿度序列饱和关联维数图Fig.5 Saturation correlation dimension of temperature and humidity

5）递归图。时间序列的递归图中存在一条主对角线，通过观察与此对角线平行的直线数量及长短能反映时间序列的可预测性。温湿度序列递归图见图6，递归范围取前250个样点，嵌入维数d取8，时延τ取1。图中与主对角线平行的线偏短，说明序列适合短期预测，不易长期预测；且温度序列递归图中平行线要多于湿度序列，表明温度的可预测性要强于湿度序列。

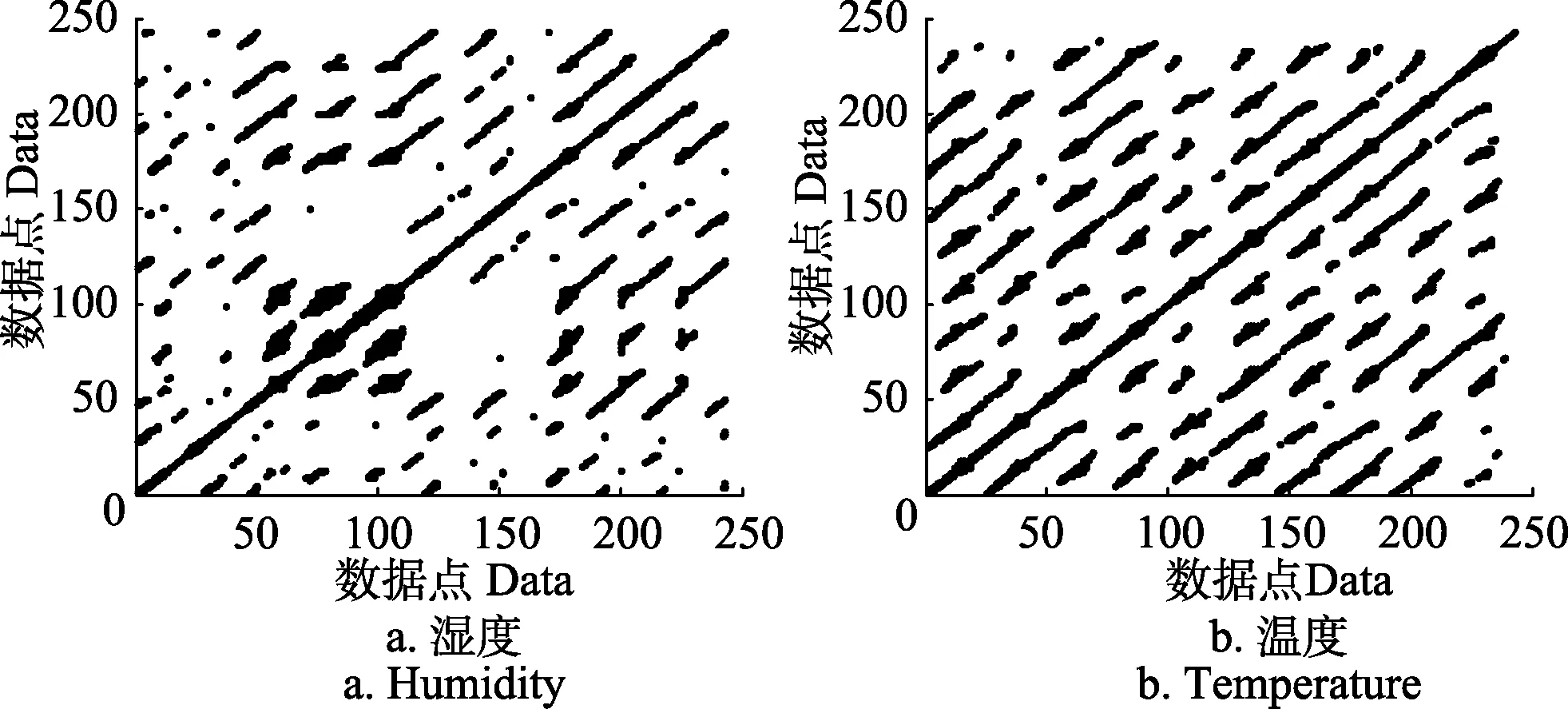
图6 温湿度序列递归图Fig.6 Recursive graph of temperature and humidity

针对以上 5种特性分析，可以验证温湿度序列具有较强的非线性、非平稳性及混沌特性。对于大自然中存在的随即时间序列，当验证其具有混沌特性时，可借助相空间重构将序列映射至高维空间获取其混沌吸引子，进而实现预测。目前验证时间序列是否具有混沌特性的充分条件并不存在，lyapunov指数、关联维数及递归图为混沌序列的3个经典指标，当满足此3个指标各自所需条件时，可近似验证此时间序列具有混沌特性。而在后续研究中，混沌序列的又一必要条件为非线性，且温湿度序列恰好具有非线性及非平稳性。因此本文首先对温湿度序列进行特性分析，在验证其可预测性后再进行预测，使研究更具实际意义。

4 预测实例及结果比较分析

现对温湿度进行预测，预测试验软件平台为Matlab2010a。针对所选试验序列，从第101时刻至第500时刻作为学习样本，从第501时刻至第900时刻作为测试样本。为了展示GPM的预测能力，本文将之与核回归（kernel-regression, K-R）、最小最大概率机回归（minimax probability machine regression, MPMR）、线性回归（linearregression, L-R）、GP和SVM模型进行比较。

K-R是一种基于核函数的预测模型，通过调整最优窗宽h，逐渐夹逼得到对应误差最小的预测结果，K-R由于其可以同时预测线性与非线性时间序列，一直作为预测模型研究的基础。MPMR无须对模型分布做具体假设，仅需知道序列分布的均值和协方差矩阵即可，此模型改善了神经网络易陷入极小值与过拟合等不足，并可以有效的预测混沌时间序列，如Sun利用MPMR预测传统混沌时间序列[32]，取得较好结果，目前MPMR已成功用在预测电力负荷时间序列及交通流量时间序列。L-R是一种非常传统的模型，利用变量之间相互依赖的定量关系，得到线性表达式，进而预测测试样本。L-R在线性较强的时间序列中表现出较好的预测效果，但对于混沌时间序列，预测效果欠佳。GP作为GPM模型的基础，已被广泛应用于各项预测中。

本文采用以下2个指标作为定量评定预测结果的优劣：

1）均方根误差（RMSE）

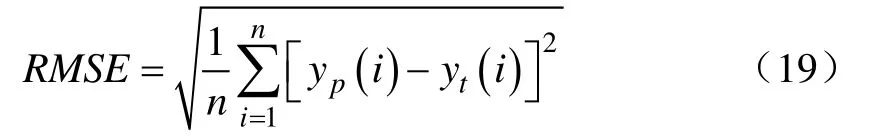
2）判定系数（ R2）

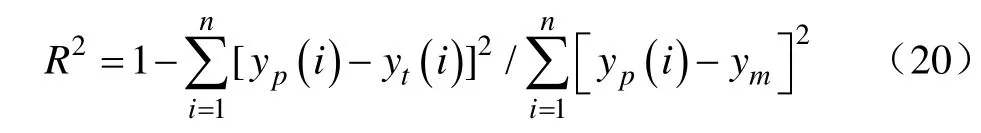
4.1 湿度预测

在GPM模型中，主要待定参数为模态个数C，加上相空间重构的参数d和τ，共有3个参数需要确定。对于湿度时间序列，为获得最佳预测参数，首先固定C值不变，将d从2至8，τ从1至6循环遍历搜索。通过对比不同d和τ下的RMSE和2R值，可以得到最优预测参数为5d=和1τ=。然后将此参数固定的前提下，循环遍历模态个数C，在同时保证RMSE最小和2R最大的前提下，最优模态个数C应取3。在获取全部最优参数后，对湿度序列进行预测，预测结果如图7所示。图7a中线为序列真实值，点线为得到的预测值，因此点、线贴合度越高，意味着预测效果越好。图7b点状图中横坐标代表湿度序列真实值，纵坐标代表预测值，图中点越集中于主对角线上，意味着预测效果越好。

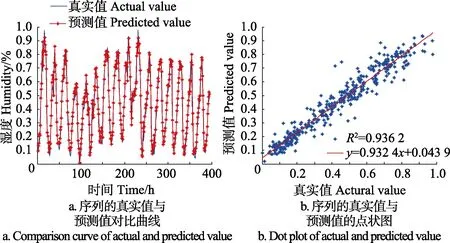
图7 湿度序列的GPM模型预测结果Fig.7 Prediction results of humidity

GPM模型的优势在于：1）对序列分而治之，通过设置模态个数能更好适应多模态时间序列；2）可以输出置信区间，提高预测结果可靠性。因此为更加直观展示序列的多模态特性和置信区间，现将不同模态个数情形下的预测结果与置信区间图排列如下。图8中以 3C= 为例，红色模态描绘上午湿度变化情况，呈急剧下降趋势；绿色模态描绘下午湿度变化情况，呈急剧上升趋势；蓝色模态描绘从下午到上午一整段的夜间湿度变化情况，先上升后下降。从图中看出，3种湿度变化趋势对应着3种模态，若不区分模态，就不易展示上述湿度变化趋势。而将之划分成多个模态预测，可以有效提升预测效果。在图9中，蓝线与红线分别代表置信区间上限与下限，2条线在波峰与波谷位置与预测曲线贴合紧密度要弱于其他位置，证明此处的预测可靠度要小于其他位置。

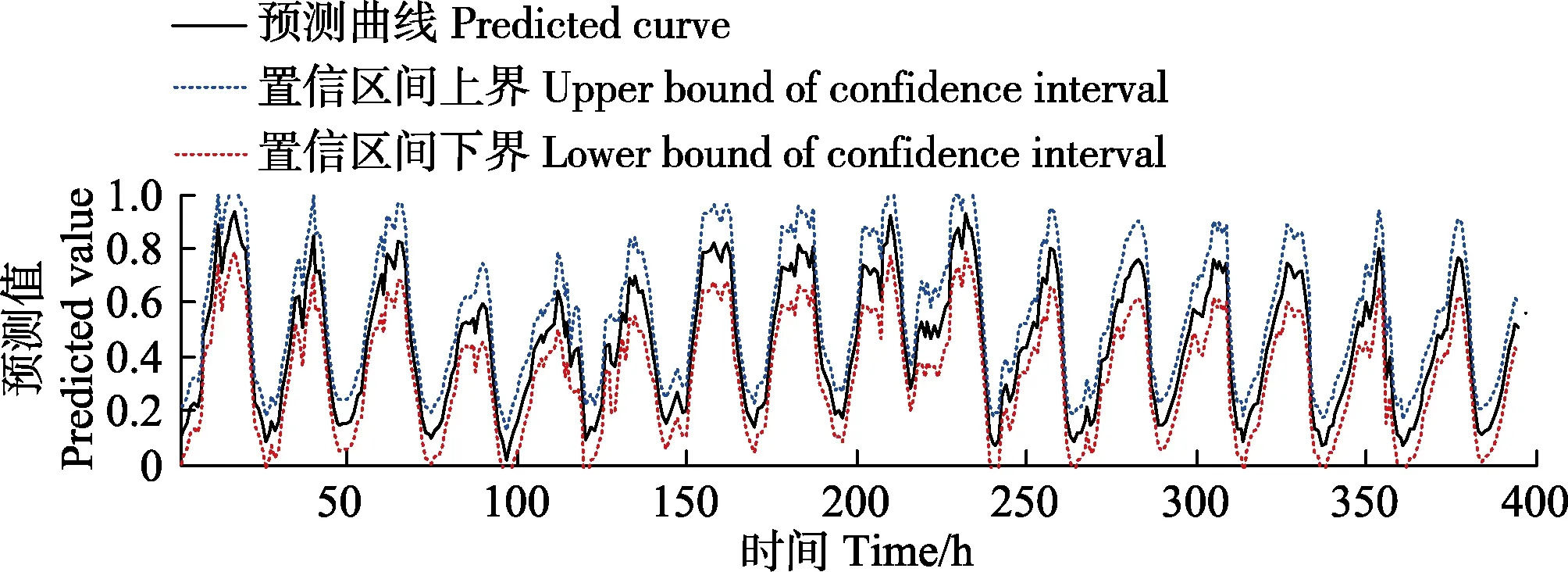
图9 湿度预测置信区间Fig.9 Confidence interval of humidity prediction

现将6种模型在最佳d和τ取值下（5d=、1τ=）的预测RMSE值、2R值及预测耗时列于表1。从表1中看出，GPM 预测效果要好于其它 5种模型。由于 GPM与SVM皆需通过迭代训练样本，因此其预测耗时要略高于其它4种模型，且GPM耗时要低于SVM。对于湿度序列，GPM 最终预测RMSE= 0 .062 0，R2= 0 .936 2，预测耗时为113.417 5 s。

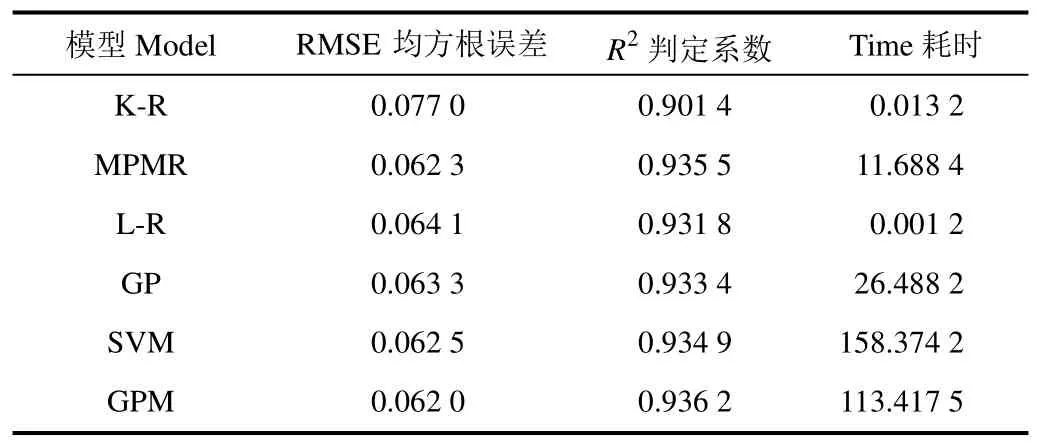
表1 6种模型湿度预测对比Table 1 Comparison of six model humidity prediction

4.2 温度预测

与湿度预测获取最佳参数过程相同，最终可得d=5、τ=1、C=2。将所有参数设置完毕后，对温度序列进行预测，预测结果如图10所示。

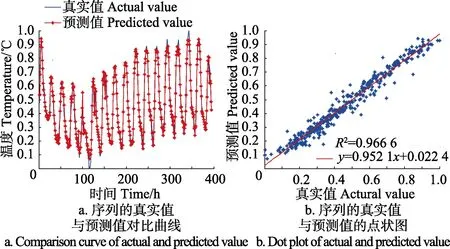
图10 温度序列的GPM模型预测结果Fig.10 Prediction results of temperature

继而针对最优d和τ（5d=、1τ=），将6种模型的预测结果列于表2。从表2中看出，GPM的预测效果要好于其它 5种模型，且温度序列的预测效果要好于湿度预测。同样由于迭代学习，GPM与SVM的预测耗时要高于其它4中模型，且GPM要低于SVM。对于温度序列，GPM预测RMSE= 0 .042 6，R2= 0 .966 6，预测耗时为90.004 9 s。

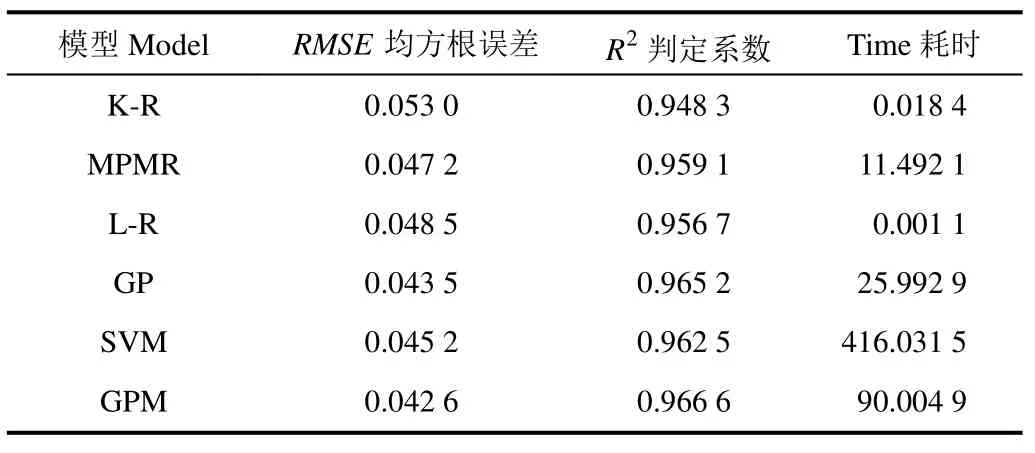
表2 6种模型温度预测对比Table 2 Comparison of six model temperature prediction

5 结 论

本文采用高斯过程混合（GPM）模型进行温湿度多模态预测，并采用真实大气温湿度序列进行预测试验及验证。得到结论如下：

1）自相关函数等5个指标揭示了温湿度序列具有很强的非线性、非平稳性、混沌特性和一定的短期可预测性；

2）随着相空间重构参数嵌入维数和时延增加和减小，预测准确率逐渐上升，但嵌入维数的取值不宜过大，预测耗时与嵌入维数、时延无明显关系；

3）GPM的模态个数取值没有明显规律。不同的温湿度序列最优模态个数也随之不同。对于本文所采用的试验序列，湿度预测时最优模态数为3，温度预测时最优模态数为2；

4）在GPM与K-R、MPMR、L-R、GP及SVM对比试验中，GPM预测效果最佳，要明显高于其它5种模型，预测效果排序为：GPM>SVM>=GP>MPMR>L-R>K-R。但由于GPM与SVM采用迭代学习算法，预测耗时要略高于其它4种模型，且GPM预测耗时要低于SVM。

[1] 周伟，李永博，汪小旵. 基于CFD非稳态模型的温室温度预测控制[J]. 农业机械学报，2014，45(12)：335－340.Zhou Wei, Li Yongbo, Wang Xiaochan. Model predictive control of air temperature in greenhouse based on CFD unsteady model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12): 335－340. (in Chinese with English abstract)

[2] 邓玲黎，李百军，毛罕平. 长江中下游地区温室内温湿度预测模型的研究[J]. 农业工程学报，2004，20(1)：263－266.Deng Lingli, Li Baijun, Mao Hanping. Forecasting model of inter temperature and humidity for intelligent greenhouses in the middle and lower reaches of the yangtze river[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(1): 263－266. (in Chinese with English abstract)

[3] 何杰颖，张升伟，张瑜. 北京地区夏季和冬季大气温度和湿度变化规律的分析[C]//中国遥感大会. 2010.

[4] 付旭云，陕振勇，李臻，等. 时变模糊神经网络及其在航空发动机排气温度预测中的应用[J]. 计算机集成制造系统，2014，20(4)：919－925.Fu Xuyun, Xia Zhenyong, Li Zhen, et al. Time-varying fuzzy neural network and its application in prediction of exhaust gas temperature[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 919－925. (in Chinese with English abstract)

[5] 庞丽藩，巩萌萌，曲洪权，等. 基于集总虚拟湿源的民机客舱湿度预测[J]. 航空学报，2012，33(6)：1030－1035.Pang Lifan, Gong Mengmeng, Qu Hongquan, et al. Moisture prediction for aircraft cabin based on lumped virtual moisture source[J]. Acta Aeronautica et AstronauticaSinica, 2012,33(6): 1030－1035. (in Chinese with English abstract)

[6] 何芬，马承伟，张俊雄. 温室湿度动态预测模型建立与试验[J]. 农业机械学报，2009，40(10)：173－177.He Fen, Ma Chengwei, Zhang Junxiong. Dynamic forecasting model of humidity in greenhouse[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(10):173－177. (in Chinese with English abstract)

[7] 王定成. 温室环境的支持向量机回归建模[J]. 农业机械学报，2004，35(5)：106－109.Wang Dingcheng. SVM regression modeling for Greenhouse environment[J]. Transactions of the Chinese Society for Agricultural Machinery, 2004, 35(5): 106－109. (in Chinese with English abstract)

[8] Pérez-Vega A, Travieso C M, Hernández-Travieso J G, et al.Forecast of temperature using support vector machines[C]// 2016 International Conference on Computing,Communication and Automation (ICCCA), Noida, 2016, 388－392.

[9] Yu Huihui, Chen Yingyi, Shahbaz G H, et al. Prediction of the temperature in a Chinese solar greenhouse based on LSSVM optimized by improved PSO[J], Computers and Electronics in Agriculture, 2016, 122:94－102.

[10] 左志宇，毛罕平，张晓东，等. 基于时序分析法的温室温度预测模型[J]. 农业机械学报，2010，41(11)：173－177.Zuo Zhiyu, Mao Hanping, Zhang Xiaodong. Forcast model of greenhouse temperature based on time series method[J].Transactions of the Chinese Society for Agricultural Machinery,2010, 41(11): 173－177. (in Chinese with English abstract)

[11] 邹伟东，张百海，姚分喜，等. 基于改进型极限学习机的日光温室温湿度预测与验证[J]. 农业工程学报，2015(24)：194－200.Zou Weidong, Zhang Baihai, Yao Fenxi. Verification and forecasting of temperature and humidity in solar greenhouse based on improved extreme learning machine algorithm[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015(24): 194－200. (in Chinese with English abstract)

[12] Liu Q, Jin D, Shen J, et al. A WSN-based prediction model of microclimate in a greenhouse using extreme learning approaches[C]//2016 18th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, 2016, 1－2.

[13] 许童羽，王泷，张晓博，等. RBF神经网络在北方日光温室湿度模拟预测中的应用[J]. 沈阳农业大学学报，2014，45(6)：726－730.Xu Tongyu, Wang Long, Zhang Xiaobo, et al. Application of RBF neural network in humidity simulation and prediction of northern sunlight greenhouse[J]. Journal of Shenyang Agricultural University, 2014－12, 45(6): 726－730. (in Chinese with English abstract)

[14] Zou Weidong, Yao Fenxi, Zhang Baihai, et al. Verification and predicting temperature and humidity in a solar greenhouse based on convex bidirectional extreme learning machine algorithm[J]. Neurocomputing, 2017, 249: 72－85.

[15] 吴曼玲，陈一飞，李琦，等. 基于灰色预测的温室地源热泵系统温度变频调控及验证[J]. 农业工程学报，2016，32(16)：183－187.Wu Manling, Chen Yifei, Li Qi. Frequency transformation and its validation of ground source heat pump system based on grey prediction of greenhouse temperature[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(16): 183－187. (in Chinese with English abstract)

[16] 张丽丽，王相友，张海鹏. 山药切片红外干燥温度神经网络预测[J]. 农业机械学报，2014，45(11)：246－249.Zhang Lili, Wang Xiangyou, Zhang Haipeng. Temperature prediction of yam under infrared drying based on neual networks[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 45(11): 246－249. (in Chinese with English abstract)

[17] 钟诗胜，雷达，丁刚. 卷积和离散过程神经网络及其在航空发动机排气温度预测中的应用[J]. 航空学报，2012，33(3)：438－445.Zhong Shisheng, Lei Da, Ding Gang. Convolution sum discrete process neural network and its application in aeroengine exhausted gas temperature prediction[J]. Acta Aeronautica et AstronauticaSinica, 2012, 33(3): 438－445. (in Chinese with English abstract)

[18] Xu B, Dan H C, Li L. Temperature prediction model of asphalt pavement in cold regions based on an improved BP neural network[J]. Applied Thermal Engineering, 2017, 120:568－580.

[19] 于广滨，丁刚，姚威，等. 基于支持过程向量机的航空发动机排气温度预测[J]. 电机与控制学报，2013，17(8)：30－36.Yu Guangbin, Ding Gang, Yao Wei, et al. Aeroengine exhaust gas temperature prediction using support process vector machine[J]. Electric Machines and Control, 2013,17(8): 30－36. (in Chinese with English abstract)

[20] 陈伟根，滕黎，刘军，等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报，2014，29(1)：44－51.Chen Weigen, Teng Li, Liu Jun, et al. Transformer winding hot-spot temperature prediction model of support vector machine optimized by genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 44－51. (in Chinese with English abstract)

[21] Nuijten A D W. Runway temperature prediction, a case study for Oslo Airport, Norway[J]. Cold Regions Science &Technology, 2016, 125: 72－84.

[22] 苑进，胡敏，柯盛，等. 基于高斯过程建模的物联网数据不确定性度量与预测[J]. 农业机械学报，2015，46(5)：265－272.Yuan Jin, Hu Min, Ke Sheng, et al. Uncertainty measurement and prediction of IOT data based on gaussian process modeling[J].Transactions of the Chinese Society for Agricultural Machinery,2015, 46(5): 265－272. (in Chinese with English abstract)

[23] 李军，张友鹏. 基于高斯过程的混沌时间序列单步与多步预测[J]. 物理学报. 2011, 60(7): 143－152.Li Jun, Zhang Youpeng. Single-step and multiple-step prediction of chaotic time series using gaussian process model[J]. Acta Phys. Sin. 2011, 60(7): 143－152. (in Chinese with English abstract)

[24] Zhou Yatong, Zhang Taiyi, Sun Jiancheng. Multi-scale gaussian processes: A novel model for chaotic time series prediction[J].Chinese Physics Letters. 2007, 24(1): 42－45.

[25] Trest V. Mixtures of gaussian processes[C]//Advances in Neural Information Processing Systems 13. Cambridge: MIT Press, 2000: 654－660.

[26] Zhou Yatong, Zhang Taiyi, Li Xiaohe. Prediction of chaotic time series based on multi-scale Gaussian processes[J].Intelligent data engineering and automated learning. 2006,4224: 183－190.

[27] 彭虹桥, 顾洁, 胡玉,等. 基于混沌粒子群—高斯过程回归的饱和负荷概率预测模型[J]. 电力系统自动化, 2017,41(21):25-32.Peng Hongqiao, Gu Jie, Hu Yu, et al. Forecasting Model for Saturated Load Based on Chaotic Particle Swarm Optimization-Gaussian Process Regression[J]. Automation of Electric Power Systems, 2017, 41(21):25-32. (in Chinese with English abstract)

[28] 周亚同，陈子一，马尽文. 从高斯过程到高斯过程混合模型：研究与展望[J]. 信号处理，2016，32(08)：960－972.Zhou Yatong, Chen Ziyi, Ma Jinwen. From Gaussian Processes to the Mixture of Gaussian Processes: A Survey[J].Journal of Signal Processing, 2016, 32(08): 960－972. (in Chinese with English abstract)

[29] Nguyen T, Bonilla E. Fast allocation of gaussian process experts[C]//Anon. Proceedings of the 31st International Conference on Machine Learning, 2014: 145－153.

[30] Yang Yan, Ma Jinwen. An efficient EM Approach to Parameter Learning of the Mixture of Gaussian Processes[M]//Guo Chengan, Hou Zengguang, Zeng Zhigang. Advances in Neural Networks–ISNN 2011. Berlin Heidelberg:Springer, 2011:165－174.

[31] 张永明，齐维贵. 供热负荷时间序列混沌特性分析及预报模型研究[J]. 物理学报，2011，60(10)：98－107.Zhang Yongming, Qi Weigui. Chaotic property analysis and prediction model study for heating load time series[J]. Acta Phys. Sin, 2011, 60(10): 98－107. (in Chinese with English abstract)

[32] Sun Jiancheng. Prediction of chaotic time series based on modified minimax probability machine regression[J]. Chinese Physics, 2007, 16(11): 3262－3270.