一种改进的激光星间链路终端指向误差在轨标定方法

程竟爽，林益明，何善宝，王海红

(1. 北京空间飞行器总体设计部，北京100094；2. 中国空间技术研究院，北京100094)

0 引 言

建立高频、宽带的激光星间链路是未来全球导航星座实现其高速数传与精密测距能力的优选技术途径[1-2]。激光星间链路终端(Laser communications terminal，LCT)在建立链路时的指向误差，即LCT出射光向量的理想指向与实际指向之间的偏差，是链路的重要指标之一。为了减小LCT的指向误差， 需要对LCT指向误差进行标定，即：1)建立LCT指向误差模型;2)获取观测数据;3)估计指向误差模型参数;4)修正LCT转动角度，减小指向误差。为了缩小LCT指向误差模型参数的真实值与地面标定值之间的差别，往往需要利用在轨观测数据进行在轨标定[3]。因此，开展LCT指向误差在轨标定方法研究具有重要意义。

在测量设备、空间机器人参数在轨标定等领域，文献[4]建立了冗余情况下的陀螺仪在轨标定模型，但其所涉及的误差因素与LCT指向误差的影响因素不同，无法直接应用于LCT指向误差的建模中。文献[5-6]设计了激励轨迹，用于估计空间机器人抓捕目标的动力学参数，但所建立的观测方程及获取的在轨观测量无法直接应用于LCT指向误差的观测数据获取中。

目前，LCT指向误差在轨标定方法中采用的指向误差模型一般包括非参数模型[7-8]与参数模型[9-10]。其中，参数模型中各参数具有明确的物理意义，模型适合反映整个工作空间内LCT指向误差与其转动角度的关系，更适合于LCT指向误差的在轨标定。2009年，美国Aerospace公司Fields等[9]建立了TerraSAR-X与NFIRE卫星激光通信试验中潜望式LCT指向误差的参数模型，考虑了粗、精指向机构的零位偏差、终端内部光学元件安装误差等误差因素，但未考虑发射光路误差因素对指向误差的影响。2014年，武凤等[10]也针对潜望式终端建立了参数模型，考虑了粗指向机构零位偏差、轴系误差对指向误差的影响，但忽略了其他误差因素对指向误差的影响。

恒星观测法[7-8,10-11]和链路观测法[9,12]是LCT指向误差在轨标定中观测数据的两种主要获取方法。其中，链路观测法是利用链路精跟踪过程指向机构的转动运动来获取对方信标光源在轨观测数据的方法，能够估计LCT实际工作空间内的指向误差，因而在LCT指向误差在轨标定中更为有效。2009年，美国Aerospace公司Fields等获取了TerraSAR-X与NFIRE卫星激光通信试验中潜望式LCT的观测数据，估计了该终端的指向模型误差参数。经修正该LCT的指向误差由2000 μrad下降到200 μrad左右。但该文献采用的激励信号受精跟踪系统限制而不能充分激励误差，导致误差参数可观测度较差，模型参数估计精度有待提升。2007年，日本JAXA的Jono等[12]对OICETS-ARTEMIS激光星间通信试验中的LCT误差参数进行了估计，通过主动摆动快速反射镜形成主动激励信号，获取了ARTEMIS上图像传感器的光斑强度分布数据，进而估计了LCT的指向误差，但未涉及对激励信号的最优设计。

本文提出一种改进的激光星间链路终端指向误差在轨标定方法，拟对LCT指向误差参数模型和在轨观测数据获取方法进行改进：1)针对现有LCT指向误差参数模型中误差因素考虑不足的问题，在建立模型时考虑光源安装误差和预指向机构快速反射镜安装误差；2)针对链路观测法中激励信号受限而不能充分激励误差的问题，将捕获过程中指向机构主动摆动时的入射光信号取代精跟踪过程中的入射光信号作为LCT指向误差激励输入信号，放宽对激励信号幅度特性的约束；以LCT误差参数的可观测度最大为目标，对捕获过程主动激励信号进行优化，旨在使LCT修正后的指向误差从改进前的200 μrad左右下降到改进后的100 μrad以内。

1 LCT指向误差建模

1.1 LCT的组成及工作原理

LCT的组成[13-14]如图1所示。

LCT之间建立链路时，发送方LCT根据本地和对方星历和姿态信息，控制指向机构转动，使得信标光经发射光路(见图2)传输，经自由空间传输至接收方LCT。接收方LCT接收的信标光经接收光路传输并在捕获及跟踪图像传感器上形成光斑，根据光斑位置控制粗、精指向机构转动，使自身视轴指向发送方。

1.2 坐标系及其转换关系建立

事实上，LCT可以描述为一个多体系统，可利用多体系统分析方法[15]建立LCT多体系统的坐标系如图3所示。包括:

1)航天器本体：包括航天器本体坐标系(SB)；

2)LCT光学平台：包括平台坐标系(SG)、望远镜坐标系(STe)、精指向机构快速反射镜坐标系(SQ)、光路中继元件坐标系(SBS)及图像传感器焦平面坐标系(SF)，其中SBS坐标系原点位于光路中继元件中心；

3)LCT方位轴系：包括方位体坐标系(SA)及方位平面反射镜坐标系(SN)；

4)LCT俯仰轴系：包括俯仰体坐标系(SE)及俯仰平面反射镜坐标系(SM)。

上述部分坐标系的具体定义与各坐标系之间的变换关系参见文献[9]。

在此基础上，对LCT发射光路中光源、预指向机构快速反射镜等元件所处的光路部分建立相应的坐标系，有

5)LCT激光光源的光轴坐标系(SL系)；

6)LCT预指向机构快速反射镜坐标系(SP系)。

SL,SP,SBS与SG之间的变换关系为

(1)

1.3 指向误差参数模型建立

文献[9]给出了含有接收光路误差条件下LCT接收光路的指向变换关系，为

(2)

式中：uF1为入射光单位向量经接收光路传输后在SF中的坐标，ur为入射光单位向量在SI中的坐标。Tre为由ur到uF1的变换矩阵，R为反射镜反射变换矩阵，MT为望远镜的放大变换矩阵。

假设SF与SL平行，对式(2)中的Tre进行逆变换，并以ul替换uF1，得到含收发共用光路误差条件下LCT的指向变换关系，为

(3)

式中：ul为激光光源出射光向量在SL中的坐标，uT1为LCT出射光向量在SI中的坐标。

则上述条件下，LCT的指向误差参数模型为

(4)

式中：δα1，δβ1分别为LCT的方位指向误差和俯仰指向误差；α0,β0分别为LCT理想指向的方位角和俯仰角，xi,yi,zi为向量ui在X,Y,Z轴的分量，θ为LCT指向机构的转动角度，Xre为收发共用光路误差参数，f1,g1分别为LCT的方位指向误差和俯仰指向误差与转动角度及收发共用光路各误差因素之间的关系。

本文在式(3)的基础上，增加描述光源安装误差和预指向机构快速反射镜安装误差的误差项，得到含收发共用光路误差和上述新增发射光路误差条件下LCT的指向变换关系为

(5)

则上述误差条件下，改进的LCT指向误差参数模型为

(6)

式中：δα2，δβ2分别为LCT的方位指向误差和俯仰指向误差；Xtr为LCT指向误差参数模型中涵盖的新增发射光路误差参数，f2,g2分别为LCT指向误差中方位指向误差和俯仰指向误差与LCT转动角度及各误差因素之间的关系。

2 LCT指向误差在轨观测数据获取

LCT指向误差在轨观测数据包括接收光路误差与发射光路误差的观测数据。本文利用改进的链路观测法获取接收光路误差的观测数据，见第2.1节；利用终端自检法获取新增发射光路误差的观测数据，见第2.2节。

2.1 接收光路误差观测数据获取

1)观测方程的建立

链路观测法中，LCT接收光路误差观测方程为

(7)

(8)

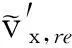
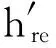
(9)

(10)

LCT指向机构转动至不同角度时，采样得到多组接收光路误差的观测数据，构成观测方程组为

(11)

式中：

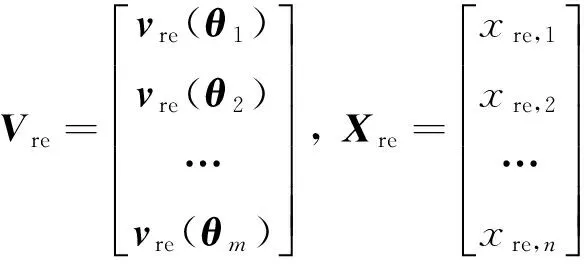
(12)

2)激励信号优化设计方法

LCT指向误差在轨标定激励信号优化问题可以表述为：设计LCT各指向机构主动摆动的角速度ω(t)=[ω1,ω2,…,ωn]T，使得LCT各指向机构按照一定的轨迹运动，LCT各指向机构的转动角度为x(t)=[θ1,θ2,…,θn]T。在该运动轨迹下，对信标光源进行观测采样得到的数据能够反映的系统可观测度κ(Cre)最大。该问题的数学描述为寻找向量ω(t)，满足

maxκ(Cre(x,ω,t))

s.t.ìîíïïïx(t)=ω(t)x(t0)=0, x(tf)=0xi(t)≤π,ωi(t)≤1

(13)

式中：t0,tf分别为LCT在轨标定时的运动起始与终止时刻。

上述优化问题是一个非线性最优控制问题，目标函数是状态向量的隐式表达，可采用伪谱法[18]。本文利用Matlab优化工具箱求解该问题。

利用本节的激励信号优化设计方法对捕获过程指向机构主动摆动的入射光信号进行优化设计，设计输入及优化结果分别见第4.1节及第4.3节。

2.2 发射光路误差观测数据获取

获取发射光路误差在轨观测数据的方法是终端自检法[19]。终端自检时，自检镜位于LCT光学头正前方，预指向机构按预定标定轨迹运动，LCT光源发射信标光，经发射光路、自检镜及接收光路构成的自检光路传输，在图像传感器上形成光斑。由LCT光源发射的信标光经自检光路传输后的向量为uF2，其与ul的指向变换关系为

(14)

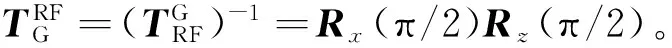
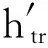
(15)

3 LCT指向误差参数估计与转动角度修正

根据式(11)，得到Xre的估计值为

(16)

式中：Wre是接收光路误差观测样本的权值矩阵。

根据式(15)，得到Xtr的估计值为

(17)

式中：Wtr是发射光路误差观测样本的权值矩阵。

代入式(5)、(7)中，得到LCT在转动角度为θ0时的指向误差估计值，为

(18)

(19)

(20)

对式(20)在θ0处一阶泰勒展开并简化， 得LCT转动角度的修正值为

(21)

4 LCT指向误差建模与在轨观测数据获取方法有效性校验

本文分别通过仿真对LCT指向误差建模、在轨观测数据获取方法及两者综合的有效性进行校验。

4.1 仿真工况参数设置

仿真分三种工况：1)无安装误差；2)仅存在粗指向机构和精指向机构快速反射镜安装误差；3)存在粗指向机构安装误差、精指向机构快速反射镜安装误差和预指向机构快速反射镜安装误差。3种工况参数如表1所示。望远镜放大倍率m= 20。

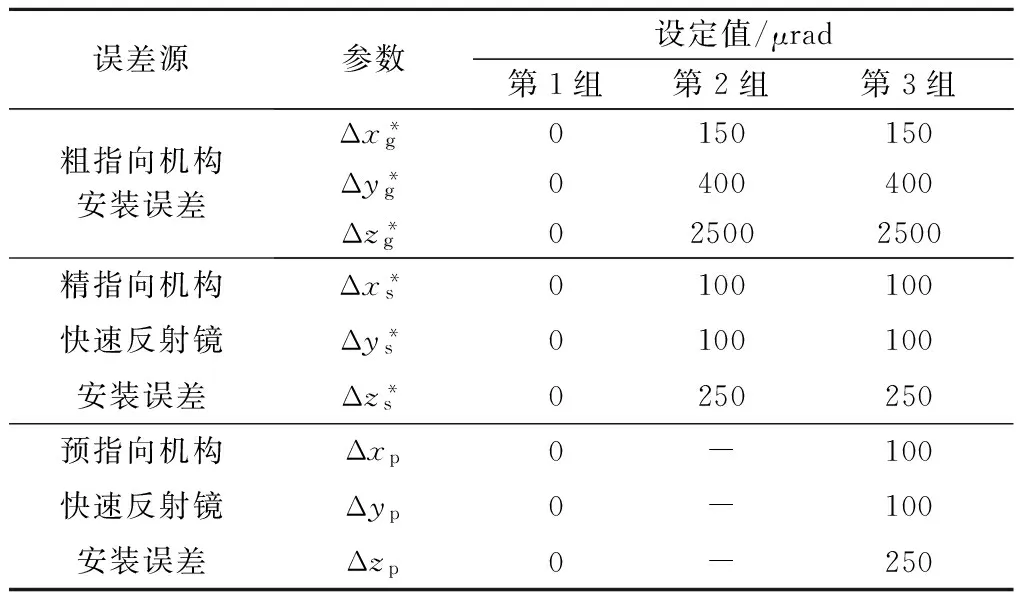
表1 LCT工况参数设置Table 1 Settings of LCT pointing error parameters

注. 表中带*号部分参数的设定值参考文献[9]的参数估计结果。

令粗指向机构的方位角与俯仰角分别在(0.5, 2.5) rad及(0, 0.5) rad的转动范围内取值，将设置的系统误差参数代入式(5)、(6)中，同时引入未建模误差δγ=50×[sinα0,cosβ0]Tμrad。捕获图像传感器测量噪声为高斯白噪声，服从分布N(0, 15) μrad。利用Monte-Carlo方法进行数值仿真，生成接收光路指向误差观测数据。

令预指向机构的方位角与俯仰角均在(0, 5) mrad的转动范围内取值，将设置的系统误差参数代入式(14)，跟踪图像传感器测量噪声服从分布N(0, 5) μrad，生成发射光路指向误差观测数据。

4.2 LCT指向误差建模有效性验证

LCT运行工况参数取为表1中的第3组设定值，利用链路观测法获取收发共用光路误差参数的观测数据并代入式(16)，利用终端自检法获取新增发射光路误差参数的观测数据并代入式(17)，计算得到各参数的估计值，修正LCT转动角度，比较模型改进前后LCT的最大指向误差。LCT指向误差各参数的估计值如表2所示。

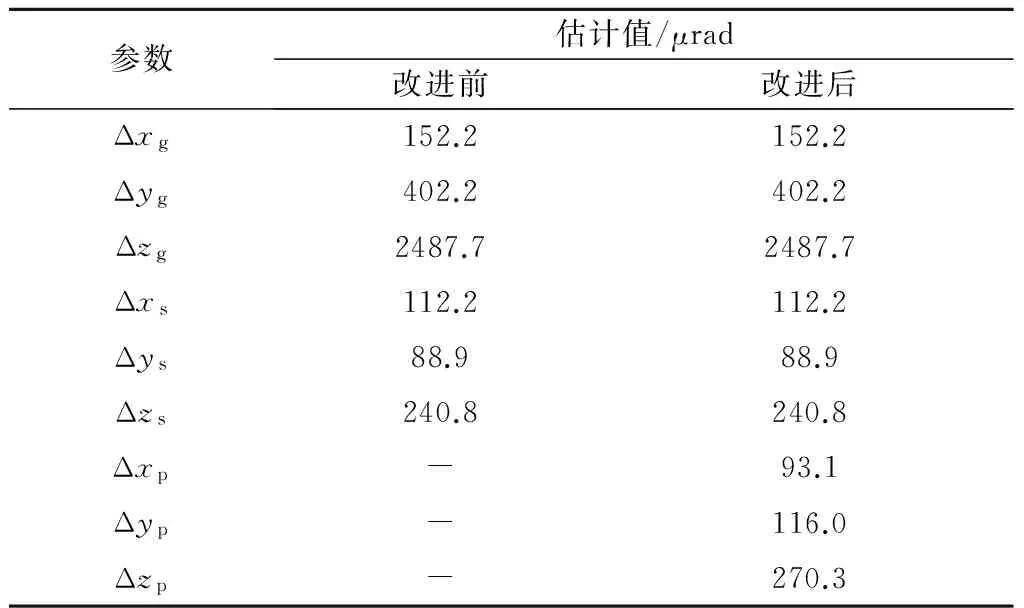
表2 LCT指向误差参数估计结果Table 2 Estimation values of LCT pointing error parameters

根据参数估计值修正LCT转动角度后，得到样本范围内修正后的LCT指向误差如图4所示。由图4可知，改进后LCT的最大指向误差(方位向)仿真结果由59.4 μrad下降到49.1 μrad；最大指向误差(俯仰向)仿真结果由62.1 μrad下降到54.4 μrad，说明改进后的指向误差参数模型更为有效。

设置LCT粗指向机构的方位角与俯仰角分别在(0, π) rad及(-π/2, π/2) rad的转动范围内取值，根据参数估计值修正LCT的转动角度，得到修正后LCT在工作空间内的指向误差，如图5所示。由图5可知，整个工作空间内，改进后LCT的最大指向误差(方位向)仿真结果由867.8 μrad下降到214.7 μrad；最大指向误差(俯仰向)仿真结果由62.1 μrad下降到54.4 μrad，说明改进后的指向误差参数模型更适合于整个工作空间内LCT指向误差的修正，进一步说明了改进后模型的有效性。这是由于改进后模型考虑了收发共用光路误差和发射光路误差，考虑的误差因素更为全面，其修正效果也更为明显。

4.3 LCT在轨观测数据获取方法有效性验证

LCT运行工况参数取表1中的第1组、第2组设置值。分别利用链路观测法和本文提出的改进观测数据获取方法获取观测数据，代入式(16)，计算得到各参数的估计值，修正LCT转动角度，比较观测数据获取方法改进前后的LCT的最大指向误差。

LCT指向误差各参数的估计值如表3所示。由表3可知，改进后系统误差参数估计值与设定值偏差的最大值由12.3 μrad下降到4.1 μrad，误差参数的可观测度由2.55×1014提高到9.60×1016。

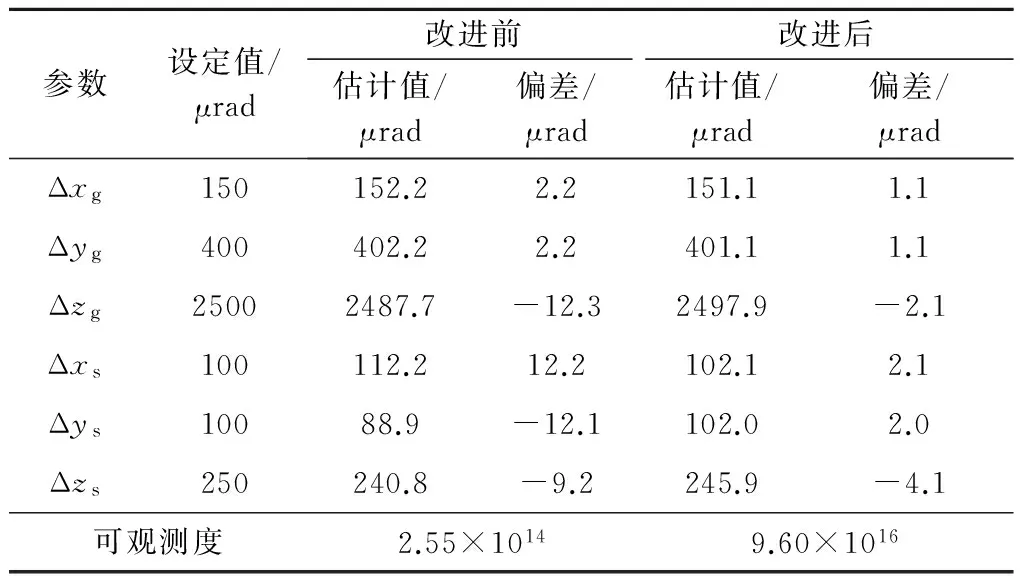
表3 LCT误差参数估计结果Table 3 Estimation values of LCT pointing error parameters

修正后样本范围内LCT指向误差如图6所示。由图6可知，改进后样本范围内LCT的最大指向误差(方位向)仿真结果由47.7 μrad下降到36.4 μrad；最大指向误差(俯仰向)仿真结果由54.5 μrad下降到51.6 μrad，说明了改进在轨观测数据获取方法的有效性。

修正后LCT在工作空间内指向误差如图7所示。由图7可知，整个工作空间内，改进后LCT的最大指向误差(方位向)仿真结果由219.2 μrad下降到115.3 μrad；最大指向误差(俯仰向)仿真结果由54.5 μrad下降到51.6 μrad，进一步说明了改进在轨观测数据获取方法的有效性。

4.4 综合验证

LCT运行工况参数为表1中的第3组设置值。利用改进的观测数据获取方法获取收发共用光路误差参数观测数据并代入式(16)，利用终端自检法获取新增发射光路误差参数观测数据并代入式(17)，修正LCT转动角度，比较LCT指向误差参数模型和在轨观测数据获取方法改进前后的LCT修正后的最大指向误差。LCT指向误差各参数的估计值如表4所示。

修正后工作空间内LCT指向误差如图8所示。由图8可知，整个工作空间内，改进后LCT的最大指向误差(方位向)仿真结果由867.8 μrad下降到112.1 μrad；最大指向误差(俯仰向)仿真结果由62.2 μrad下降到51.5 μrad，进一步说明了改进标定方法的有效性。

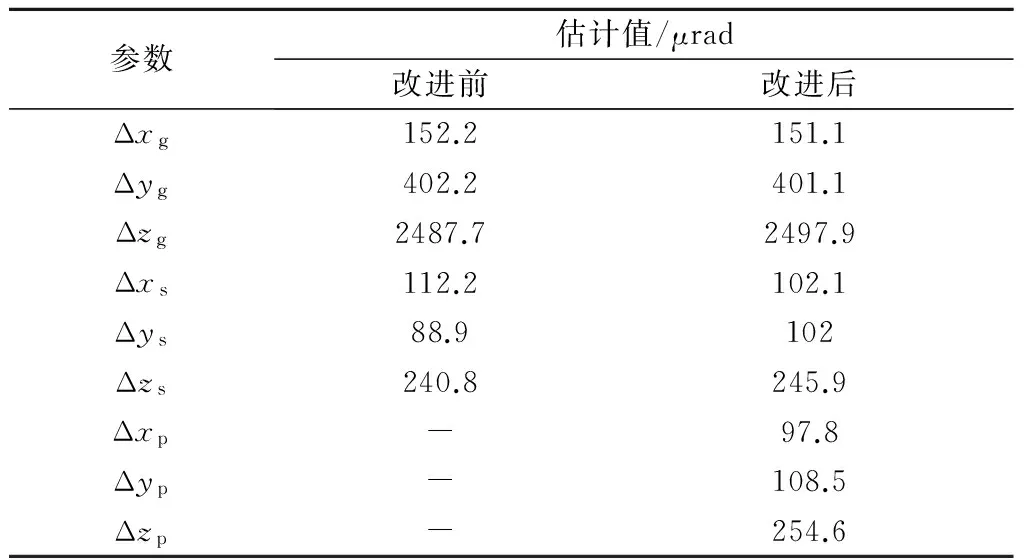
表4 LCT指向误差参数估计结果Table 4 Estimation values of LCT pointing error parameters

5 结 论

本文提出了一种改进的激光星间链路终端指向误差在轨标定方法，包括LCT指向误差建模、在轨观测数据获取、指向误差参数估计和LCT转动角度修正4个方面。经仿真校验， LCT的最大指向误差(方位向)仿真结果由改进前的867.8 μrad下降到改进后的112.1 μrad；最大指向误差(俯仰向)仿真结果由改进前的62.1 μrad下降到改进后的51.5 μrad。验证了本文提出的改进标定方法的有效性。

[1] 陈忠贵，帅平，曲广吉.现代卫星导航系统技术特点与发展趋势分析[J].中国科学(E辑：技术科学)，2009，39(4)：686-695.[ Chen Zhong-gui，Shuai Ping，Qu Guang-ji.The technology characteristic and development trend of modern navigation satellite system[J].Science in China(Series E：Technological Sciences)，2009，39(4)：686-695.]

[2] 林益明，何善宝，郑晋军，等.全球导航星座星间链路技术发展建议[J].航天器工程，2010，19(6)：1-7.[ Lin Yi-ming，He Shan-bao，Zheng Jin-jun，et al.Development recommendation of inter-satellite links in GNSS[J].Spacecraft Engineering，2010，19(6)：1-7.]

[3] Pittelkau M E.Autonomous on-board calibration of attitude sensors and gyros[C].The 20th International Symposium on Space Flight Dynamics, Annapolis,Maryland,Sep 24-28,2007.

[4] 杨华波，张士峰，蔡洪.空间冗余陀螺仪在轨标定方法[J].宇航学报，2010，31(1)：104-110.[Yang Hua-bo，Zhang Shi-feng，Cai-Hong.An in-flight calibration for redundant inertial measurement gyroscope[J].Journal of Astronautics，2010，31(1)：104-110.]

[5] 金磊，徐世杰.空间机器人抓取未知目标的质量特性参数辨识[J].宇航学报，2012，33(11)：1570-1576.[Jin Lei，Xu Shi-jie.Inertial parameter identification of unknown object captured by a space robot[J].Journal of Astronautics，2012，33(11)：1570-1576.]

[6] 罗建军，薛爽爽，马卫华，等.空间机器人抓捕目标后动力学参数辨识研究[J].宇航学报，2016，37(1)：1411-1418.[Luo Jian-jun，Xue Shuang-shuang，Ma Wei-hua，et al.Dynamic parameter identification of free-floating space robots after capturing targets[J].Journal of Astronautics，2016，37(1)：1411-1418.]

[7] Nielsen T T，Oppenhaeuser G.In orbit test result of an operational optical intersatellite link between ARTEMIS and SPOT4，SILEX[C].SPIE Free-Space Laser Communication Technologies XIV,San Jose,USA,Jan 20-25,2002.

[8] Takashi J，Yoshihisa T，Nobuhiro K，et al.OICETS on-orbit laser communication experiments[C].SPIE Free-Space Laser Communication Technologies ⅩⅤⅢ，San Jose,USA,Jan 21-26,2006.

[9] Fields R，Lunde C，Wong R，et al.NFIRE-to-TerraSAR-X laser communication results：satellite pointing，disturbances，and other attributes consistent with successful performance[C].SPIE Sensors and Systems for Space Applications Ⅲ，Orlando,USA,Apr 13-17,2009.

[10] 武凤，于思源，马仲甜，等.星地激光通信链路瞄准角度偏差修正及在轨验证[J].中国激光，2014，6(1)：154-159.[ Wu Feng，Yu Si-yuan，Ma Zhong-tian，et al.Correction of pointing angle deviation and in-orbit validation in satellite-ground laser communication links[J].Chinese Journal of Lasers，2014，6(1)：154-159.]

[11] Yu S Y， Wu F， Tan L Y， et al.Static position errors correction on the satellite optical communication terminal[J].Optical Engineering，2017，56(2)：026112.

[12] Jono T，Takayama Y，Koyama Y，et al.In-orbit test results of the inter satellite laser link by OICETS[C].The 25th AIAA International Communications Satellite Systems Conference, Seoul, South Kores, Apr 10-13, 2007.

[13] Lange R，Smutny B.Homodyne BPSK-based optical inter-satellite communication links[C].SPIE Free-Space Laser Communication Technologies ⅪⅩ and Atmospheric Propagation of Electrom-agnetic Waves，San Jose,USA,Jan 20-25,2007.

[14] 刘立人.卫星光通信Ⅰ：链路和终端技术[J].中国激光，2007，34(1)：3-20.[ Liu Li-ren.Laser communication in spaceⅠ：optical link and terminal technology[J].Chinese Journal of Lasers，2007，34(1)：3-20.]

[15] 张智永，周晓尧，范大鹏.光电探测系统指向误差分析、建模与修正[J].航空学报，2011，32(11)：2042-2054.[ Zhang Zhi-yong，Zhou Xiao-yao，Fan Da-peng.Analysis, modeling and correction of pointing errors for electro-optical detection systems[J].Acta Aeronautics et Astronautics Sinica，2011，32 (11)：2042-2054.]

[16] Yu Z S，Cui P Y， Zhu S Y.On the observability of Mars entry navigation using radiometric measurements[J].Advances in Space Research，2014, 54(8): 1513-1524.

[17] 杨海燕，汤国建.双目视觉导航信息的可观测性分析[J].宇航学报，2013，34(2)：207-213.[Yang Hai-yan，Tang Guo-jian.Observability analysis of binocular vision navigation information[J].Journal of Astronautics，2013，34(2)：207-213.]

[18] 杨雅君，廖瑛，刘翔春.航天器转动惯量参数在轨辨识的最优激励[J].国防科技大学学报，2014，36(5)：39-43.[Yang Ya-jun，Liao Ying，Liu Xiang-chun.Optimal excitation trajectories for spacecraft’s moment of inertia parameters on-orbit estimation[J].Journal of National University of Defense Technology，2014，36(5)：39-43.]

[19] Burnside J，Conrad S，Pillsbury A，et.al.Design of an inertially stabilized telescope for the LLCD[C].SPIE Free-Space Laser Communication Technologies ⅩⅩⅢ，San Jose,USA,Jan 22-27,2011.