一种捷联惯导系统加速度计时间延迟参数标定方法
2018-03-10邵会兵申亮亮
邵会兵,王 彬,申亮亮
(北京控制与电子技术研究所,北京100038)
0 引 言
惯性导航系统是一种应用广泛的导航系统,主要通过测量飞行器在惯性参考系的加速度和角速度,将其对时间进行积分,并变换到导航坐标系中,得到飞行器在导航坐标系中的位置、速度和姿态角等信息。它的性能指标好坏直接关系到系统的制导精度[1-4]。捷联惯性导航系统(Strapdown inertial navigation systems,SINS)部件少、结构简单,实现了惯导系统体积、重量、成本、可靠性方面的突破,具有广泛的应用前景。
研究惯性器件误差的标定和补偿技术是提高SINS的导航精度的主要方法之一[5-8]。传统误差标定和补偿算法的隐含条件是假设惯性传感器的采样是理想的,即不存在空间上和时间上的同步误差。空间同步误差主要是指三只加速度计敏感点不重合引起的尺寸效应(或称为内杆臂)误差,可以通过研究尺寸效应引起导航速度误差的规律,设计基于角运动激励的尺寸效应标定方案,实现对加速度计尺寸效应参数的有效估计和补偿[9-10]。时间上的同步误差主要是由于加速度计和陀螺仪的传递函数相频特性不一致引起,加速度计的数学模型在低频段可近似为一阶系统,在低频段具有较明显的线性相位延迟特点。一般情况下石英挠性加速度计的带宽为数百赫兹而光学陀螺的带宽达数千赫兹,其中相频特性差异必然会导致信号测量的时延差别,即使在后端信号调理环节通过相同的数字滤波器,也难以实现两类信号的同步。此外,由于A/D或I/F量化采样、信号预处理和信号传输等其他众多环节的影响,其中有些延时环节是考虑不周或较难准确建模的,也会致使加速度计还可能存在更大的时延影响。
为减小加速度计时间延迟的影响,本文在现有方法基础上研究了一种加速度计时间延迟参数标定方法方案,充分利用SINS滚转角运动下导航速度误差与时间延迟参数之间的关系,实现加速度计时间延迟参数的标定和补偿。
1 基于系统测试的加速度计时间延迟参数标定原理
如果已知加速度计的传递函数模型,则可很方便地将时间延迟计算出来,但是实际中获取加速度计传递函数的途径一般都比较复杂,且未考虑其在SINS系统中与陀螺的相对相位关系以及其他众多时延因素[9]。在实验室条件下,通过加速度计时延激励出导航速度误差的最简单方法是进行滚转角运动,即当SINS的某一坐标轴处于水平并绕其旋转时,加速度计敏感的比力在载体坐标系上将不断地改变方向。
设oxryrzr为参考坐标系,其水平轴oxr、ozr保持水平,指向角(方位角)为ψ(未知),当SINS使用的三个加速度计型号相同时,三个轴向的时间延迟相同,所以时间延迟后的加速度计敏感轴也是正交的。当初始时刻惯组本体系与oxryrzr重合,绕oxr旋转、角速度为ω,当转至角度γ时。设加速度计确定的坐标系为oyAzA,陀螺仪确定的本体坐标系为oybzb。
由图1可知:
(1)
式中:τ即为加速度计的时间延迟。
假设转台在转动前已经调平好,则oyAzA下的加速度计输出为:
(2)
式中:Lx,Ly分别表示绕x轴和y轴的旋转矩阵,
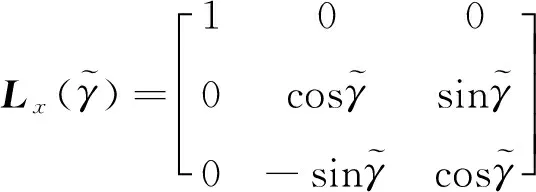
(3)
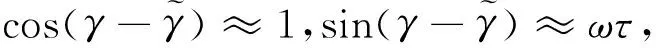
(4)
理想情况下,导航系下输出的视加速度信息为:
(5)
根据速度误差方程
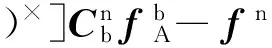
(6)
式中:(φ)×表示向量φ的叉乘矩阵。
不考虑失准角φ的影响,则有
(7)
令ω>0,转台转动角度为2π。则北向和东向速度为:
(8)
据此得到水平速度表达式:
(9)
当转动过程中进行导航计算(或事后处理),即可利用水平速度信息完成加速度计时间延迟τ的标定和补偿。
2 影响导航速度误差的主要误差因素分析
但是在滚转角运动过程中,除了时间延迟误差外,实际SINS的导航速度误差还会受到其他各种误差因素的影响,主要包括:初始对准误差、加速度计测量误差(刻度系数误差、零偏误差、安装误差和尺寸效应误差)和陀螺仪测量误差(刻度系数误差、常值漂移误差和安装误差)。为了实现时间延迟参数的精确标定,需要对误差源进行全面的建模与分析。
2.1 加速度计误差分析
2.1.1加速度计刻度系数
当加速度计刻度系数误差为KA=diag(kx,ky,kz)时,有
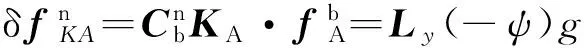
根据
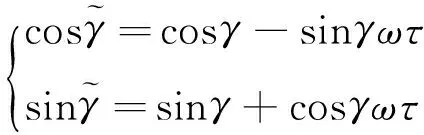
旋转一圈后速度误差为:
(10)
2.1.2加速度计零偏
(11)
2.1.3加速度计安装误差
(12)
2.1.4加速度计尺寸效应
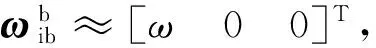
(13)
转一圈后的速度误差为:
(14)
即在滚转条件下尺寸效应引起的加速度计误差可以忽略。
2.2 初始对准误差分析
初始对准完成后,系统失准角误差对加速度计输出影响如下:
(15)
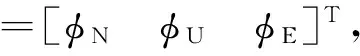
(16)
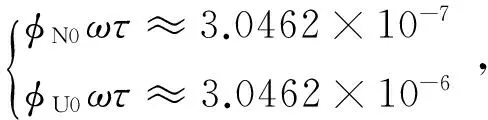
(17)
2.3 陀螺仪误差分析
陀螺误差影响失准角输出,设惯组三个轴向的陀螺仪漂移为εx,εy,εz,陀螺仪误差对失准角的影响可以表示为:
根据式(15),速度误差可表示为:
(18)
2.3.1陀螺仪常值漂移
设三个方向的常值漂移为εx 0,εy 0,εz 0,其在导航坐标系下投影为:
(19)
根据式(18),转动一圈后的速度误差为:
(20)
2.3.2陀螺仪刻度系数
设三个方向的陀螺刻度系数为kgx,kgy,kgy,其引起的陀螺测量误差在导航坐标系下投影为:
(21)
根据式(18),转动一圈后的速度误差可表示为:
(22)
2.3.3陀螺仪安装误差
综上所述,在航向角ψ=0,速度误差可进行充分简化,载体旋转一周后的东向和天向速度误差可以表示为:
(23)
(24)
式中:kVE2=2π2gεx0,kVE1=2π2gkgx-πg(Δyz-Δzy)-2πgφN0,kVE0=[2πg+πg(ky+kz)]τ,kVU1=πg(ky+kz)-2π2gεx0τ,kVU0=[πgτ(Δyz-Δzy)-2π2gkgxτ]。
3 加速度计时间延迟参数标定
由式(23)可知,利用kVE0可以得到时间延迟τ的估计值,但要扣除π(ky+kz)的影响;式(24)中kVU1=[πg(ky+kz)-2π2gεx0τ],根据50型激光惯组的精度指标,当陀螺漂移ε≈0.065°/h和加速度计刻度系数误差ky/z≈1×10-4时,若时间延迟为3 ms,则
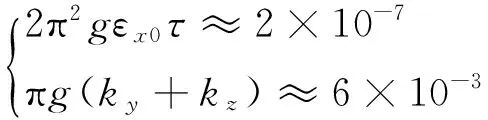
前者的影响可以忽略不计,得到π(ky+kz)≈kVU1/g,因此得到时间延迟τ的估计值为:
(25)
具体的标定方案为:在一次通电状态下,转台绕滚转轴旋转3圈(最少为3圈,也可以转n>3圈),三次旋转的角速度不同,设为ω1,ω2,ω3;每转完一圈后东向和天向速度分别为δVE1,δVE2,δVE3和δVU1,δVU2,δVU3。二者的表达式为:
(26)
4 数学仿真及结果分析
4.1 数学仿真条件
1) 误差参数(3σ)
捷联惯组的参数参照50型激光捷联惯组给出,设陀螺仪的零偏稳定性为0.065°/h,刻度系数稳定性5×10-5,安装误差20″;加速度计的零偏稳定性为10-4g0,刻度系数稳定性10-4,安装误差15″;初始对准的水平姿态角误差1′,航向角误差10′;加速度计相对陀螺仪的时间延迟设定为3 ms。
2) 位置、姿态和角速度信息
初始的纬度、经度和高程为30°,120°和10 m;转台处于水平面,方位角为0°;三轴速率转台的最高转动角速度为60°/s;当地重力为9.7931696 m/s2。
4.2 仿真结果分析
1) 不同方位条件下结果
在不同的方位角条件下,以10°/s转动一圈,利用式(9)求时间延迟参数,结果如表1所示。
从表1可以看出,在0°条件下的时间延迟标定误差最小。根据误差分析可知,0°条件下东向速度也主要受加速度计的刻度系数误差、安装误差影响,误差源相对较少,因此利用东向速度误差得到的时间延迟参数精度较高。仿真结果验证了理论分析的正确性。
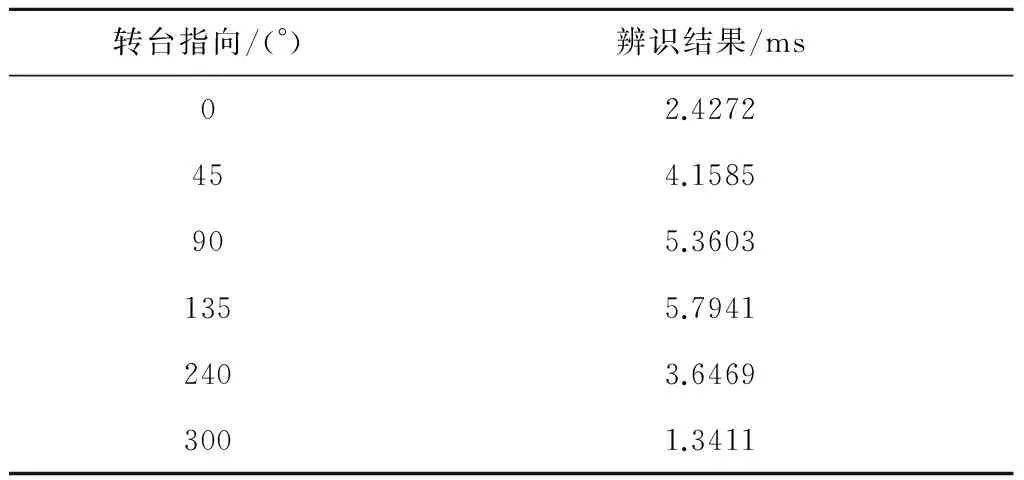
表1 不同方位下的时间延迟辨识结果Table 1 Time-delay parameters calibration results under different oriertations
2) 不同转速条件下结果
在0°方位角、不同转速条件下,利用式(9)求时间延迟参数,结果如表2所示。
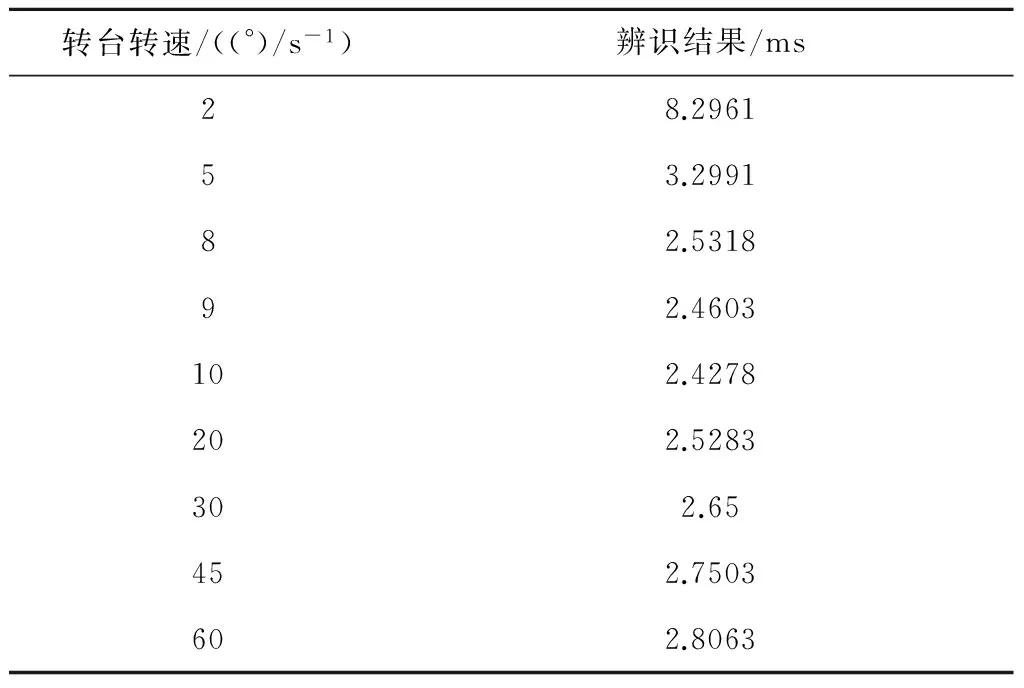
表2 不同转速下的时间延迟辨识结果Table 2 Time-delay parameters calibration results under different rotation velocities
从表2可以看出,随着转速的增加,时间延迟的标定精度逐渐提高,分析表明当转台转速较低时,转动一圈时间较长,惯性器件误差累积会影响水平速度输出,导致时间延迟参数标定精度变差;当转速增大时,转台旋转一圈仅需要十几秒时间,惯性器件的累积误差影响较小,因此标定精度提高。但是考虑到转台限速、加速至需要的加速度耗时等问题,辨识时间延迟时选择的角速度大小10~30°/s较为合适。
从仿真结果也可以看出,转动一圈后,仅利用水平速度进行参数辨识的精度较低,10~30°/s旋转条件下的三次时间延迟的均值仅为2.5 ms左右,因此需要进一步借助最小二乘算法来提高辨识精度。
3) 时间延迟误差辨识方法验证
10°/s,20°/s和30°/s滚转条件下的导航结果见表3。
根据式(25)得到的时间延迟τ的估计值为:
可以看出,最小二乘算法获得的时间延迟结果要远远优于单次旋转或将多次结果求平均的方法。
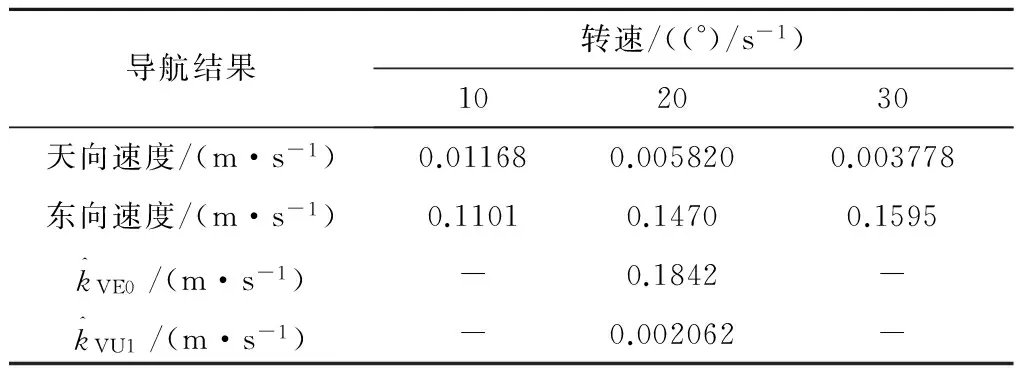
表3 滚转条件下的导航结果Table 3 Navigation results under rotation angular motion
20°/s旋转角运动条件下,在惯性导航算法中引入加速度计时间延迟补偿前后的速度误差曲线如图2所示(只给出东向速度,另外两个方向不明显)。可以看出延时补偿后的速度误差明显减小,说明了时间延迟补偿的有效性。
5 结 论
本文研究了一种在滚转角运动环境下进行加速度计时间延迟参数标定的方法。在现有方法基础上,充分考虑滚转角运动过程中SINS的各种误差因素的影响,得到影响时间延迟参数辨识的主要误差因素。该方法实际操作和数据处理简单、可行。数学仿真结果表明,该方法可精确标定SINS加速度计时间延迟参数,验证了理论分析的正确性和方案的可行性。
[1] 冯培德. 论混合式惯性导航系统[J]. 中国惯性技术学报, 2016, 24(3):281-24. [Feng Pei-de. On hybrid inertial navigation systems[J]. Journal of Chinese Inertial Technology, 2016, 24(3): 281-284.]
[2] 申亮亮, 王新龙. 弹道导弹SINS空中在线标定方法[J]. 航空兵器, 2009(2):3-7. [Shen Liang-liang, Wang Xin-long. An in-flight calibration method of ballistic missile SINS[J]. Aero Weaponry, 2009(2): 3-7.]
[3] 周潇, 杨功流, 蔡庆中. 基于小波神经网络的高精度惯导重力扰动补偿方法[J]. 中国惯性技术学报, 2016, 24(5):571-576. [Zhou Xiao, Yang Gong-liu, Cai Qing-zhong. Compensation on gravity disturbance for high-precision INS based on wavelet neural network [J]. Journal of Chinese Inertial Technology, 2016, 24(5): 571-576.]
[4] Wang X L, Wang B, Li H N. An autonomous navigation scheme based on geomagnetic and starlight for small satellites[J]. Acta Astronaut, 2012, 81: 40-50.
[5] 于海龙, 吕信明. 激光捷联惯导系统高阶误差模型的建立与分析[J]. 红外与激光工程, 2013, 42(9):2375-2379. [Yu Hai-long, Lv Xin-ming. Establishment and analysis of high-order error model of laser gyro SINS[J]. Infrared and Laser Engineering, 2013, 42 (9): 2375-2379.]
[6] 杨晓霞, 黄一. 激光捷联惯导系统的一种系统级标定方法[J]. 中国惯性技术学报, 2008, 16(1):1-7. [Yang Xiao-xia, Huang Yi. Systematic calibration method for laser gyro SINS[J]. Journal of Chinese Inertial Technology, 2008, 16 (1): 1-7.]
[7] 任新建, 杜亚宁, 张睿. 激光捷联惯导高阶误差模型菜蔬系统级辨识[J]. 弹箭与制导学报, 2016, 36(5):17-20. [Ren Xin-jian, Du Ya-ning, Zhang Rui. High order error model parameters systerm-level identification of laser strap-down inertial navigation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36 (5): 17-20.]
[8] 郑永杰, 王勇, 曹梦丹. 捷联惯导系统光学陀螺带宽不一致研究[J]. 宇航学报, 2016, 36(9):1024-1029. [Zheng Yong-jie, Wang Yong, Cao Men-dan. Study on inconsistent frequency bandwidth of optical gyroscope in SINS[J]. Journal of Astronautics, 2016, 36 (9): 1024-1029.]
[9] 严恭敏, 张强,何昆鹏,等. 捷联惯导系统中加速度计的时延补偿研究[J]. 宇航学报, 2013, 34(12):1578-1583. [Yan Gong-min, Zhang Qiang, He Kun-peng,et al. Study on time-delay compensation for accelerometers in SINS[J]. Journal of Astronautics, 2013, 34 (12): 1578-1583.]
[10] 钟明飞. 振动环境中激光陀螺惯导系统误差分析与补偿技术研究[D]. 长沙: 国防科技大学, 2013. [Zhong Min-fei. Error analysis and compensation techniques of RLG INS under vibration environment [D]. Changsha: National University of Defense Technology, 2013.]
