基于Frank-Copula贝叶斯估计的系统性风险对样本标度的敏感性分析

赵 宁,于方坤，由 申，汪振双

(1.东北财经大学金融学院，辽宁 大连 116023；2.东北财经大学投资工程管理学院，辽宁 大连 116023)

1 引言

现有模型研究中，个体投资者行为满足均值-方差理论依然是最常用的假设，但现实数据却存在随机的资产组合结算日期，同时拥有单一标度和结算日期的假设过于严格，势必影响度量的准确性[1]。Fama-French三因子模型提出之后, 许多学者把它用于美国、中国及许多其他国家的股票市场中, 实证发现,FF 三因子模型能很好解释由公司规模和账面市值比排序的投资组合的平均收益率的大多数截面变动[2]， beta系数被认为是实证研究中系统风险值的有效衡量指标[3]。但，该模型亦并未详述时间期限长度或者时间标度，而这是投资者赖以决策的关键。目前大多数的资产定价检验中，标度都是固定的和外生的，如月度数据，同时投资回报也通过月度度量。追溯到该惯例的来源，主要是由于证券价格研究中心(The Center for Research in Security Prices, CRSP) 第一次录入数据时只有月度数据可得,而随着日度数据的可得，也发现行为发生的明确顺序在高频数据中难以捕捉，且交易不同步问题、买卖价差问题都对采用高频数据的估计结果造成影响。

大量的实证检验表明，样本标度是主观选取的，如果数据(回报率)满足独立同分布，m期样本标度下所估计的Beta值则与n期样本标度下的Beta具有显著差异[4]。模型采用不同的样本标度，才能尽可能的完善对系统性风险Beta值的估计[5]，Handa等[6]证明了当采用依据规模排序的资产组合月度数据时，对CAPM的检验被拒绝，而采用相同的组合年度数据时，F检验则不会被拒绝。如果当采用年度回报估计β时，长期投资标度因素(包含了市场回报)能够被定价，但是当采用月度数据时则不能[7]。Darollesa和Gourierouxb[8]出于期限的不一致性考虑，在其投资组合的研究中将机构投资标度与个体投资标度区分处理；Lina和Liub[9]在针对台湾某种共同基金的研究中提出为了接近真实的投资标度减少误差，以月度收益数据取代周度数据进行实证计算。

Lee等[5]指出以投资回报作为原始数据的样本受到样本标度的影响，提出了可以对样本标度进行估计的研究思路。Lin 和Chen[10]提出以贝叶斯估计法考察投资标度比λ对β值的影响，取代了前人一直采用的稳定参数思路，但单期CAPM模型的局限性作用削弱了Beta值的估计准确性，而规模和市盈率对其影响并没有被考虑，而多数的研究在该问题上依然采取主观选取样本标度的方法[11]。

本文构建了FF-三因素—样本标度比模型，在针对系统性风险beta值的研究中加入样本期限比参数，作为期限长度识别指标，在不采用先验性假设的前提下，延续并改进了Lee等[5]和Lin和Chen[10]的研究思路，提出基于Frank-Copula结构的贝叶斯估计方法，拟合数据的非正态特征，使用Copula函数取代贝叶斯估计中的正态函数，通过系统风险与投资标度之间的联合后验分布结果，对依照市盈率排序的5组投资组合其系统风险Beta值对样本标度的敏感性分析差异。原有研究结果显示资产组合转手率较低，投资标度比是否对当前系统性风险Beta值具有影响，其影响结构如何，需要实证结果予以检验[10,12]。

该研究对于系统性风险度量方面颇具应用价值。随着全球一体化的加强，系统风险加剧，各国有关机构对于系统性风险度量进度的要求不断提高，数据样本标度是实证研究永远不可回避的关键性问题。多项实证结果表明[4-8]，样本标度的差异直接影响系统性风险值度量精度，将样本标度考量在系统性风险的度量中，有利于从数据角度提高实证研究中系统性风险的精确度。同时，依据正态假设，现有数据特征通常无法满足正态分布假设，而以此获得的后验分布结果自然存在偏差，本文以Frank-Copula函数代替贝叶斯估计中的原有正态多元结构，以Frank-Copula结构拟合构成的联合后验分布展示不同标的样本特征，展示系统性风险值与样本标度动态影响关系，试图探寻不同标的物所遭遇系统性风险对样本标度选取的敏感程度差异，进而分析我国资本市场所遭受的系统性风险的结构特征，对未来量化投资提供数据支持。

2 样本标度作用机理

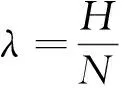
E(HRj) = [E(NRj)]λ

(1a)

E(HRm) = [E(NRm)]λ

(1b)

E(HRf) = [E(NRf)]λ

(1c)

其中λj为证券j的投资标度比由于观察标度为常量，其波动直接反映真实标度波动，用以控制Nj与Hj之间的差异。大量的实践检验证明[2-3,13]，资产组合需要考虑资产规模、账面市值比效应，随着实证研究的深入，Fama-French 三因素模型在实证研究中的贡献愈加突出，现选用该模型作为基础模型，并相应加入样本标度因素。

E(Rjt)-Rft=βj[E(Rmt)-Rft]+sj(SMBt)+hj(HMLt)+ξj,t

(2)

式中，Rmt表示时间下的市场组合收益率，Rft表示t时间下的无风险报酬率，Rjt表示所研究的资产组合j在t时间下的报酬率，E(Rmt)-Rft是市场因子，表示的是市场风险溢价，SMBt为t时间下的规模因子组合收益率，HMLt表示t时间下的账面市值比因子组合收益率。βj，sj，hj，分别为系统性风险值、规模因子、账面市值比因子的系数。我们假设：

(3)

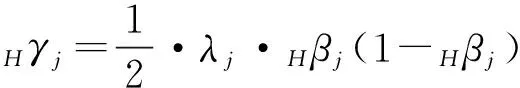
(4)

其中λj为证券j的投资标度比参数，用以控制Nj与Hj之间的差异：

[E(NRjt)]λ-(HRft)λ=βj[E(HRmt)λ-(HRft)λ]+sj(SMBt)+hj(HMLt)+ξj,t

(5)

当λj→1时，投资标度预估值无限接近投资标度真实值，当λ→0时，原有模型退化为瞬时风险收益模型[1,5]。如果存在一个λ，且该参数不能被忽略的话[7]，则需要具有一个平方项的超额市场回报，以对数处理及欧拉扩展可以将原有模型转化为非线性形式，进而采用常替代弹性函数(Constant elasticity of substitution, CES)将Fama-French 三因素模型转化如下：

log[E(NRjt)]-logNRjt=Hβj[logE(NRmt)-log(NRft)]+sj(SMBt)+hj(HMKt)+Hγj[logE(NRmt)-logE(NRft)]2

(6)

如果模型中的投资标度是非零变量，那么，风险与收益之间明显呈现非线性关系，(6)中，右侧等式的第二项表示变量之间的相关性关系，而(4)则表示系统风险受投资标度差异所造成的影响，由前人研究[1,4-5,10]可知Hγj与系统风险Hβj呈现动态相关，所以采用贝叶斯方法以获得λ与β的联合后验分布进行分析。

3 Copula贝叶斯估计

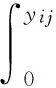
Copula贝叶斯估计以基于Copula的多元函数获得联合后验分布，Clayton Copula可以建立低尾相关的结构模型，我们将Clayton Copula 对应的以分布函数形式的似然函数表达如下：

(7)

(8)

当低迷期相关时，Y的各分量之间(各产业的收益)之间会出现低尾部相关，对应繁荣期相关Gumbel Copula:

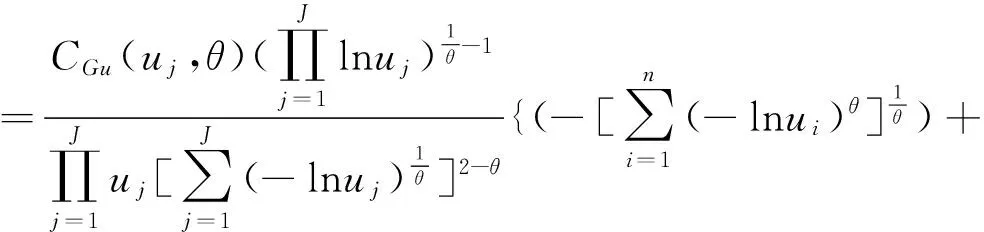
(9)

当J=2可以推导出等式 (8) 中似然函数模型，并依照 (9) 化为多重积分模型。而复苏过渡状态时，双向相关的Frank Copula可以建立联合分布下的似然函数。

(10)

似然函数只能表示为复杂积分形式，针对ζj获得边际密度函数，并通过积分化简Copula结构自身参数。

测试数据组1表示了贝叶斯估计所得联合后验分布结果(图1)，图1-1所示为基于普通贝叶斯估计所得的联合后验分布，图1-2为基于Frank Copula结构的联合后验分布，图1-3，图1-4分别表示基于Clayton和Gumbel Copula结构的联合后验分布。由于数据本身的特征，即使我们分别使用不同的相关结构函数进行拟合，所获得的联合后验分布相关特征近似，即主观选择了不同的Copula相关结构而导致相关结构被主观决定，相反,我们更能检验出在不同的数据特征面前，Copula函数的拟合优度，而多元正态结构在一定程度上掩盖了数据特征；当数据本身不具有特殊的相关特征时，即使我们选择不同的Copula来拟合联合分布，所获得的联合后验分布与正态结构所获得的联合分布则非常近似。

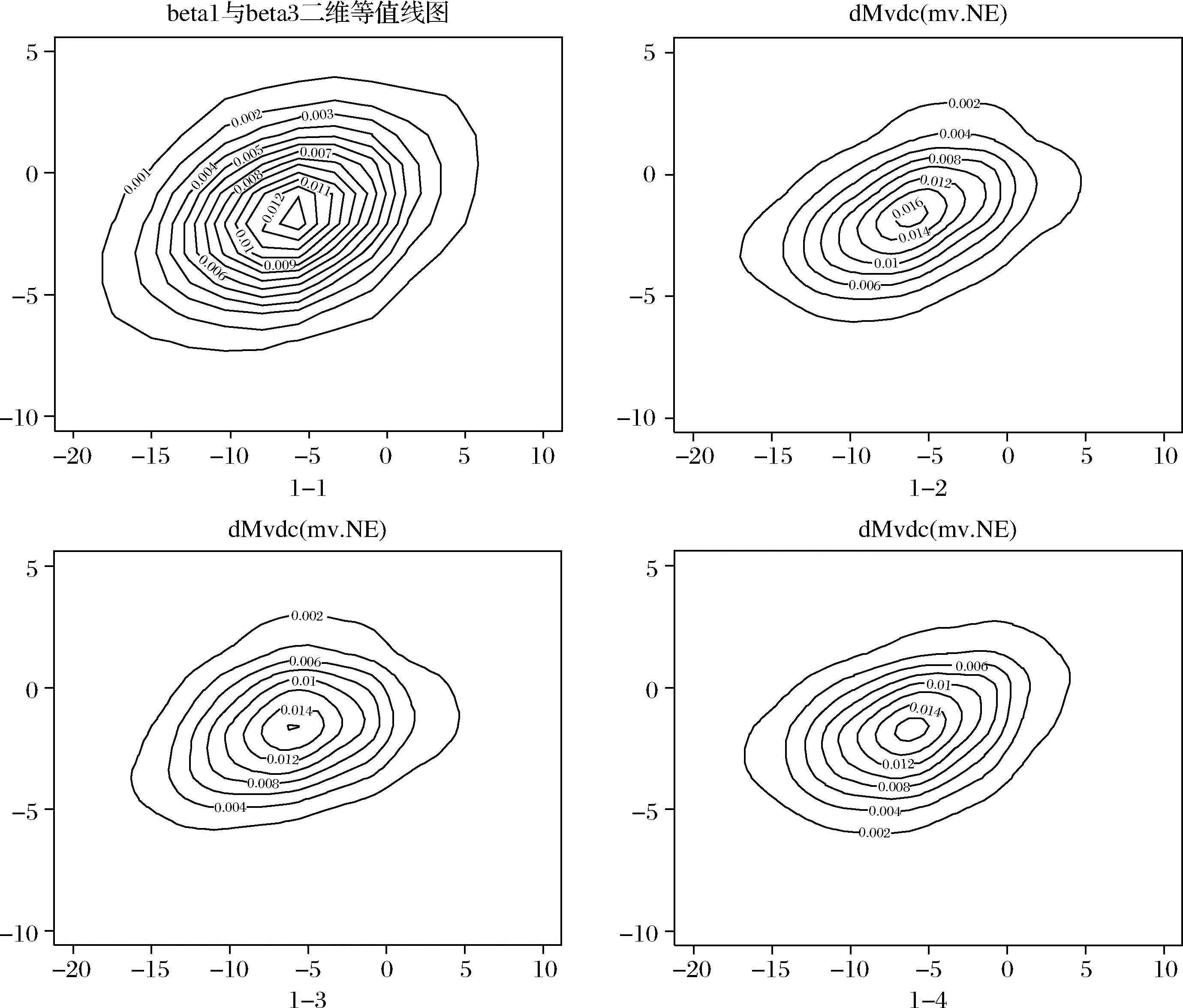
图1 基于正态、Frank，Clayton，Gumbel结构的联合后验分布

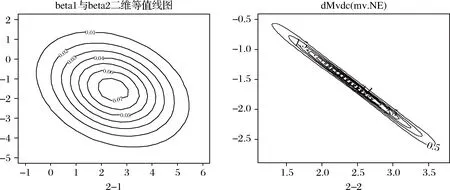
图2 测试数据组联合后验分布

图2表示了测试数据组2——分别拟合多元正态结构与Frank Copula的联合后验分布，可以看出在正态结构下因子之间呈现弱负向相关关系；但Frank Copula所获得的联合后验分布则由于参数θ的控制，因子呈现中心区域增强结构的强相关，这种局部强相关的特征来自数据本身，而由于正态假设该特征可以被掩盖起来。因此，本文选用了能够同时囊括正负相关结构的Frank Copula建立联合后验分布。

4 实证分析

我们借助Wild数据库，选取上海证券交易所A股市场中500只股票月收益率，2009年1月30日至2015年12月31日，公司6月末和12月末的总市值ME，及其年末(12月31日)的账面价值BE。2008年后全球经济在经历过金融危机后处于一个逐渐复苏的大环境中，相对前人研究，现阶段样本颇具代表性及研究价值。数据以总市值和账面价值比分成25组：首先根据每年6月底股票的总市值ME，将样本股票等分为5组，再按照账面市值比BE/ME将每组股票由高到低等分成5组，由此就得到25个组合。

本文以上证综指收益率构建Rmt，将每组的20支股票分为6个组合，即首先依据第t年6月底股票的总市值ME，将样本股票均分为大(B)和小(S)两组，将两组再按第t-l年末的账面市值比BE/ME的值分为高(H)、中(M)、低(L)三组，权重比例分别为30%，40%，30%，形成SL、SM、SH、BL、BM、BH，6组股票组合，计算从t年7月到t+1年6月的月收益率，权重为个股总市值占组合总市值比，风险因子可以通过下式得出，模型化为(14)：

(12)

(13)

Y=HβjX1t+sjX2t+hjX3t+HγjX4t

(14)

4.1 数据规模效应特征及样本标度的存在

如表1所示，组合月平均超额收益率由0.5%-3.2%，超额收益率随公司规模的增大而降低；超额收益率随账面市值比的增加而增高。

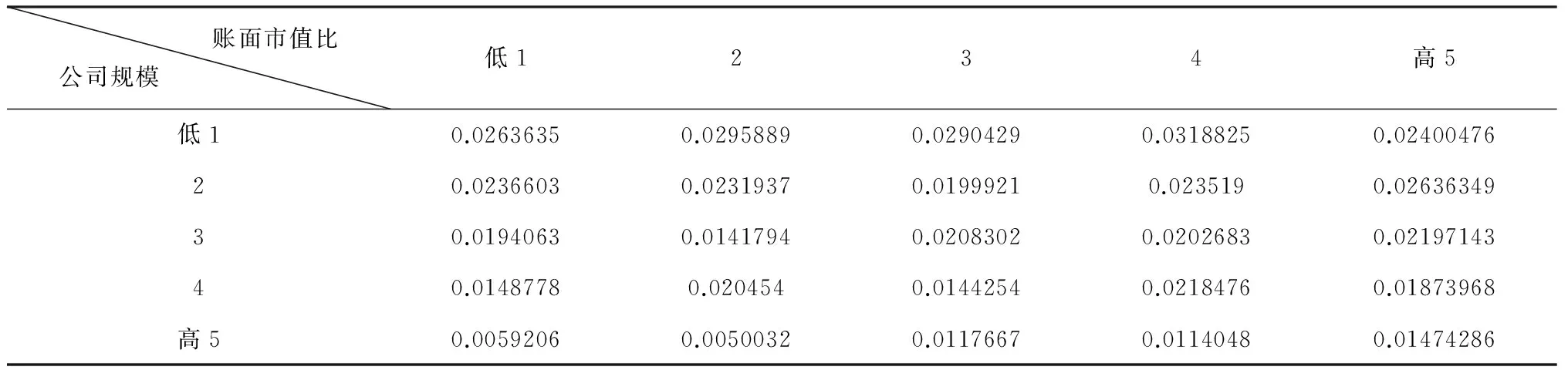
表1 组合月超额收益率均值

4.2 基于样本标度比的SUR估计结果

表2表示由SUR估计所得的参数结果、t统计量、调整后的模型拟合优度Adjusted R-squared及F值回归参数。显著性水平为5%时，截距项趋于零，80%不显著，与理论假定一致；随着公司规模增大，超额收益越低，随着账面市值比提高，超额收益增大。

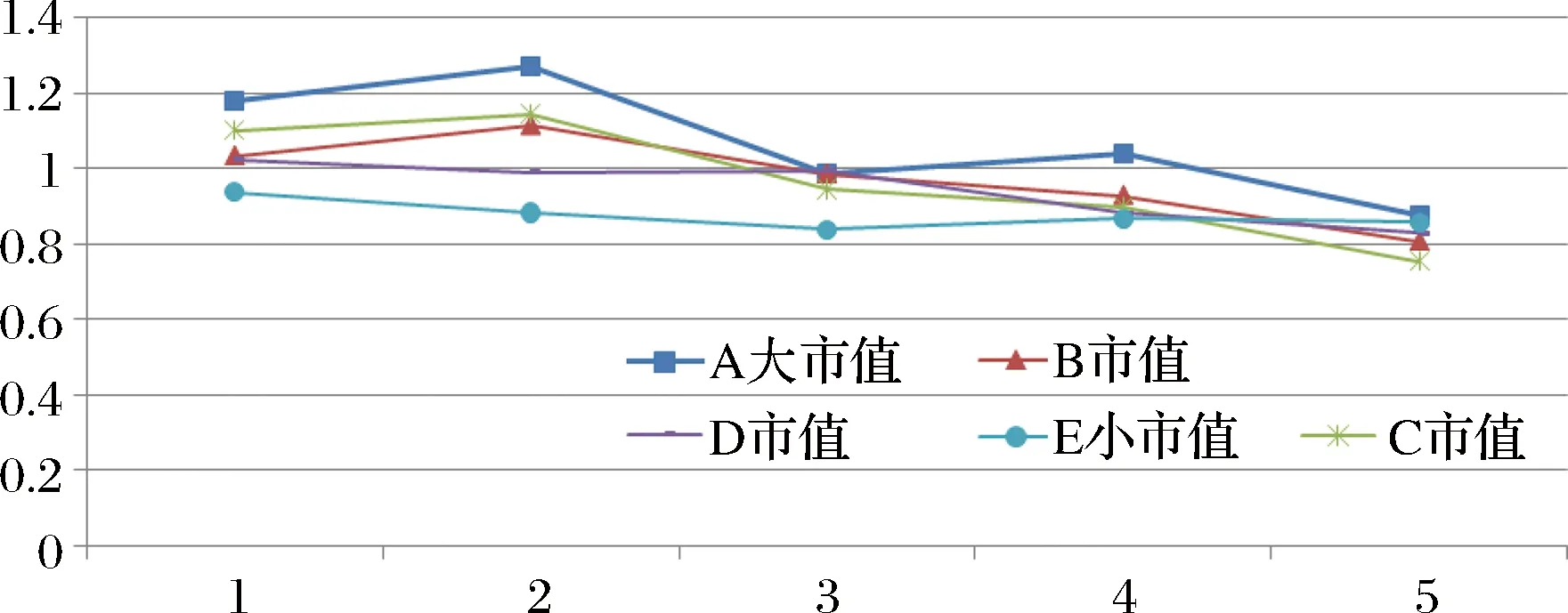
图3 基于SUR估计的Beta值差异

市值因子SMB斜率s值，呈先增大后减小趋势，账面市值比过高，负向影响投资者热情，控制账面市值比因素后，s值与组合市值趋向负相关，风险随着规模的扩大而增加。t统计量5%的显著性水平下80%显著，即数据存在明显的规模效应。当公司规模一定时，账面市值比因子HML的斜率h值随着市值比的增高而减小，账面市值比因子HML的t值在5%的显著性水平下有88%是显著的。结合超额收益率、市值因素和账面市值比，能够解释组合超额收益变动。模型回归拟合优度较好，加入样本标度校正的模型拟合优度R2都在0.81以上。显著水平5%下，表2 F统计量超过F (4,63)≈2.53。结合图3可以认为，Fama-French三因素投资标度模型对我国上证A股市场有效，规模效应和账面市值比效应存在。

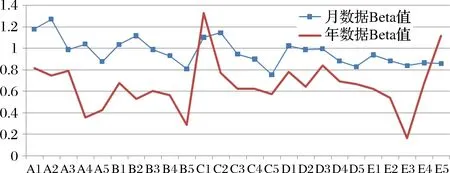
图4 月、年标度数据Beta值差异

有图4可见，由年数据所得beta值几乎均小于月数据Beta值，这也证实了前人研究者关于样本期限作用存在的结论，由于选取收益率数据频率(日数据、周数据、年数据)的不同，所估计Beta呈现非稳定性特征，即数据样本标度直接影响系统风险Beta值的估计准确性，而该影响的特征和灵敏度对于风险度量方向研究尤为重要。

4.3 敏感度影响分析

本文旨在确认Fama-French三因素投资标度模型对我国上证A股市场有效的基础上，分析投资标度对系统性风险度量精确度的影响。根据表2、表3分析其适用性，及数据相关性，通过Copula贝叶斯估计方法以获得Beta值的边际后验分布，以及依据公司规模与账面市值比排序的β值与投资期限比λ的波动变化，进而分析样本标度对Beta值的影响作用是否存在超额收益效应，及规模效应。

本文采用R软件实现Copula贝叶斯估计进行蒙特卡洛模拟，模拟数据量为10000，采样点为1001至10000。估计结果如图5，图6：β的边际分布非对称，无风险的发生概率为零，风险资产其系统风险非零，期望回报率不能用无风险回报率表示；2、由于无信息先验假设的采用，β的边际后验分布的期望值与参数SUR估计结果接近。

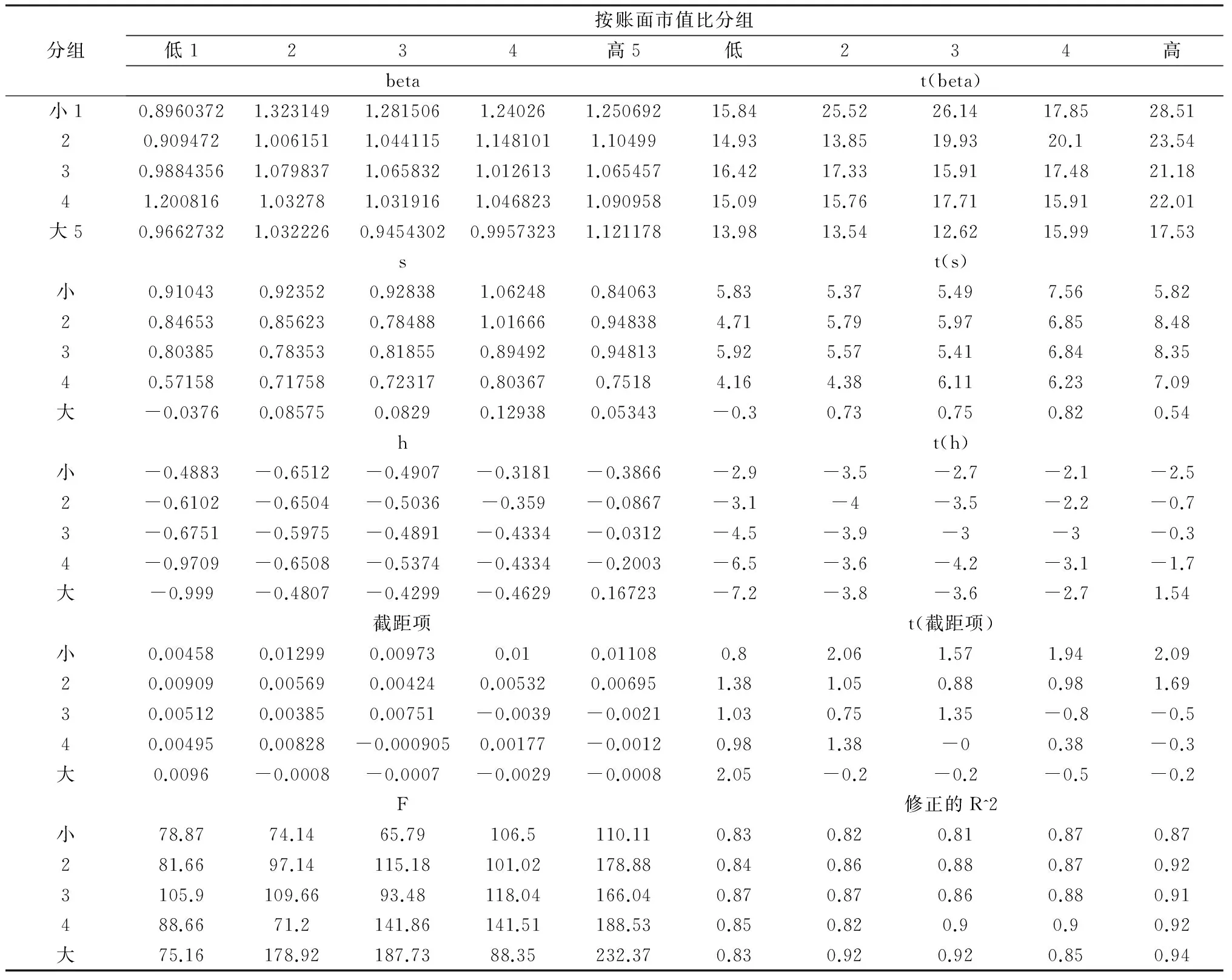
表2 Fama-French三因素模型参数回归结果

图5表示Copula贝叶斯估计所得基于样本标度的Beta值边际后验分布，依据窗口宽差异，其Beta风险值随着账面市值比(A1-A5)的减小，其均值点左移，即账面市值比越小的数据其Beta值越小，且随着账面市值比的减小，Beta值趋于稳定，即gama标度比参数对账面市值比较大的数据影响远高于市值比小的组合。而在纵向比较其对应的规模效应发现，随着公司规模的减小，其Beta分布剑锋部分向左移动，且存在较明显的右偏斜，且其散度减小。即随着账面市值比的下降其Beta值的稳定性显著提高；同时公司规模的增大增加了Beta值。

图6中，等高线纵坐标gama表示投资期限比(即样本标度)参数，横坐标表示系统性风险参数beta值。copula贝叶斯方法所获得的联合分布的波动中心值比较接近， 25个组合数据之间的相关程度所带来的影响，使得选择SUR方法进行参数估计更加精确。通过运用copula贝叶斯方法所获得的联合分布中，无论是系统性风险参数beta还是投资标度参数gama，都是在中心结果的一定范围内进行波动。

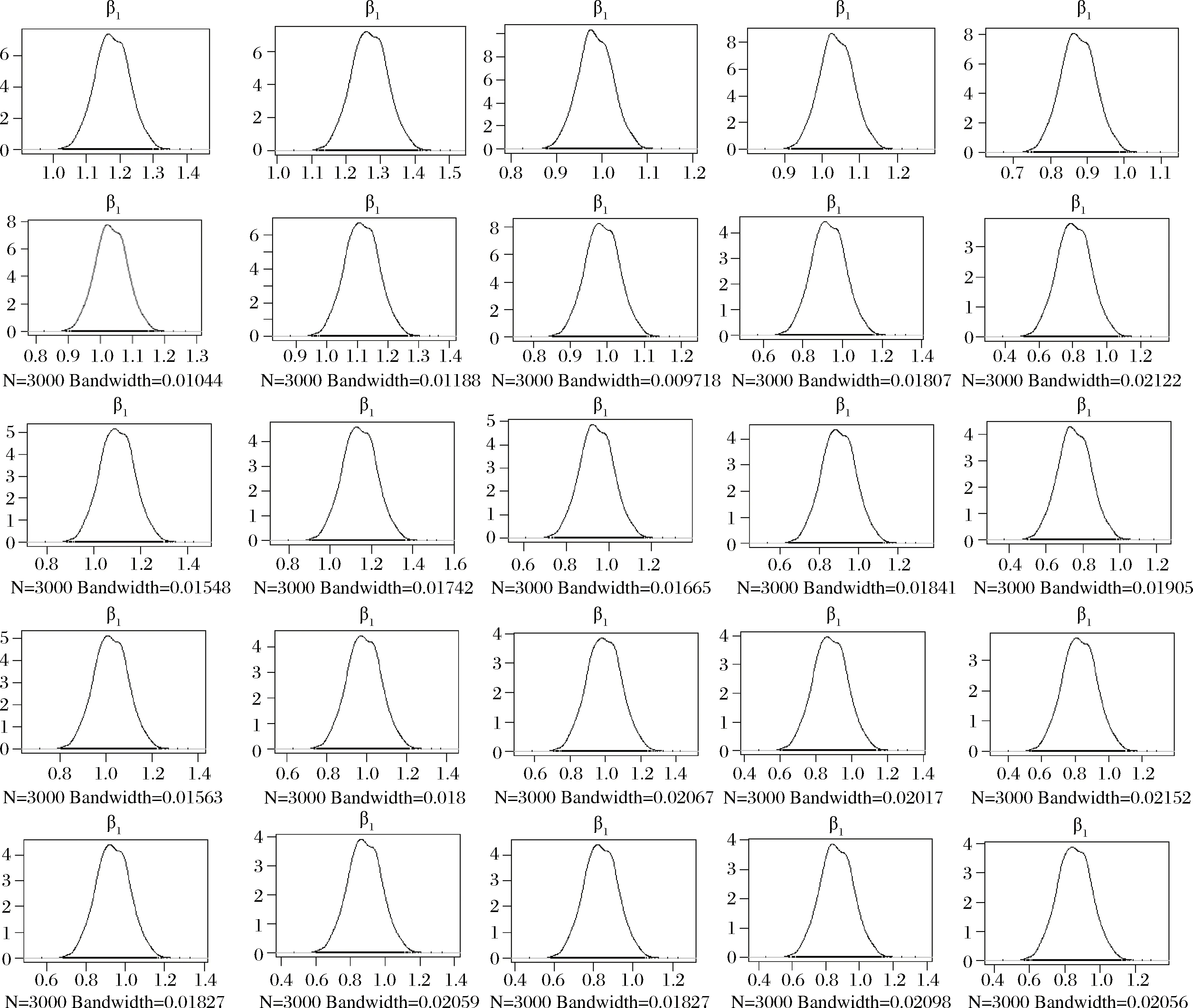
图5 投资组合风险系数Beta边际后验分布

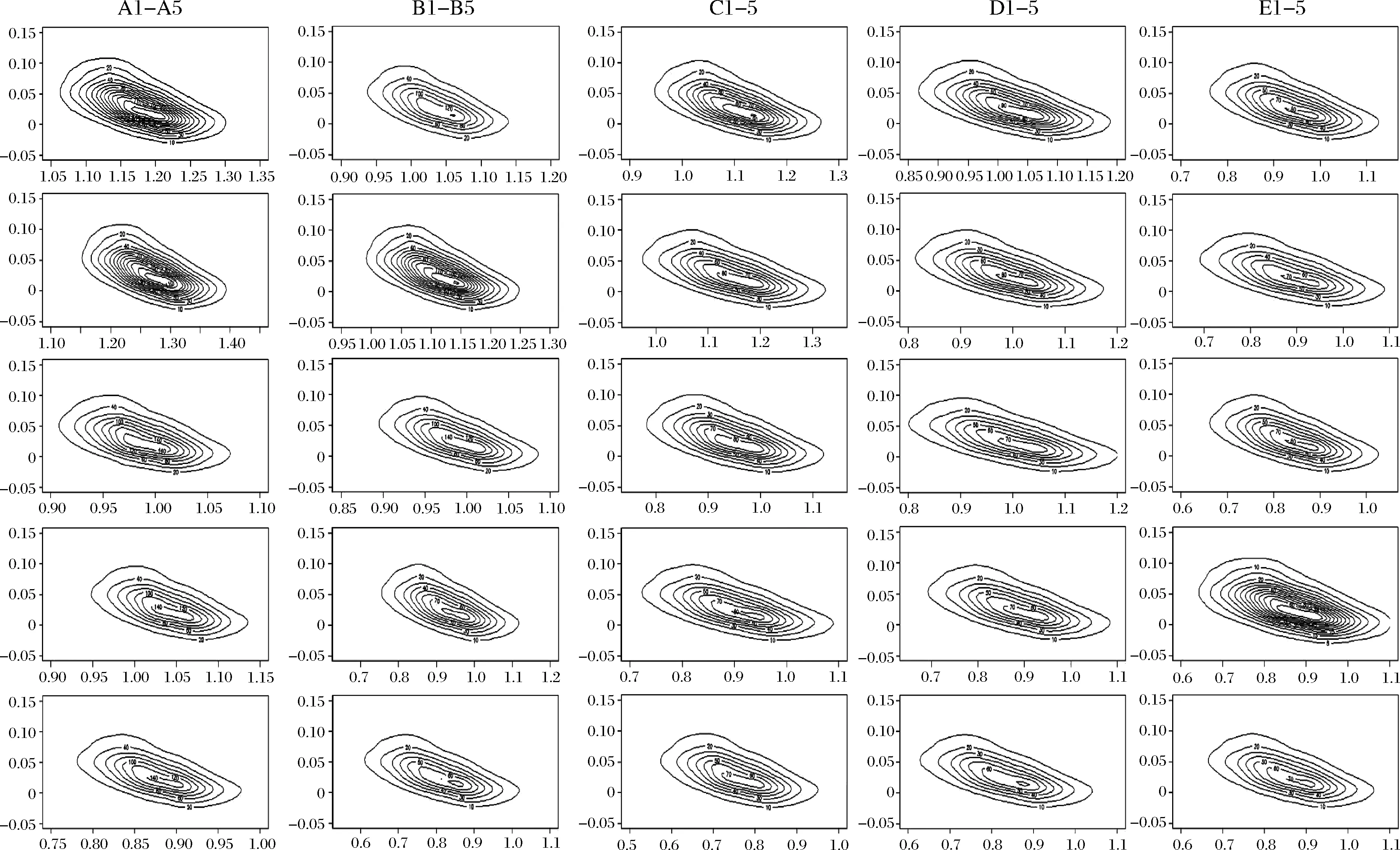
图6 组合标度比联合后验分布图

通过结果我们得出，相比较贝叶斯Copula方法得出的结论，虽然参数估计能够更加直观的给出数据结果，但是通过贝叶斯Copula方法得到的联合分布结果我们可以清楚的看到25个资产组合的系统风险值和投资标度的核心值及其波动范围，更能判断两者之间的相关关系。运行所得Frank copula参数值为-0.1560751，25个资产组合的系统性风险参数β值与投资标度gama呈现弱的负相关关系，投资标度相对比较稳定，在其所受到的系统性风险的变化幅度内做出了微小的改变。

对比现存美国市场数据，通过FF三因素投资期限模型得到投资期限比参数与系统性风险参数在各行业中均具有正相关关系的结论，即对于投资者持有的资产组合，系统性风险的不断增大，使得他们更难根据自己计划的时间来获得收益，他们实际的投资期限和原本计划好的投资期限的差别在明显的增大。我国系统性风险参数beta值与投资标度gama呈现负相关关系，且程度相对较弱。美国市场其主流为机构投资者，周转率趋于延长，而我国目前为止依然以小型投资者占据市场主流，投资期限趋于缩短，采用以月数据为基础数据的模型进行实证检验，所得样本标度比波动范围小，且其增大会减小系统风险值，即依据月度数据，我国投资者转手率较高，其真实投资期限较短，与美国年度周转率有显著差异。

首先，在美国市场经济体制下，美国政府很少会直接干预金融市场发展，其机构投资者在市场形成过程中逐步壮大，资本市场以机构投资者占比为主流，而中小散户占比较小，长线投资稳定投资作为左右市场价格的主要力量[14]，所以依据现有研究数据其系统风险值随标度比增加而增大，且存在明显的行业差异，资产决策受年尾效应明显。

而我国资本市场中，政府监管更为严格，利率市场化进程还没有完全成熟的融入资本市场的运作当中，“重股市，轻债市，重国债，轻企债”的现象依然存在。机构投资者受分业经营框架的影响，还没有真正的占据市场的主流。如果说美国资本市场是养老基金、投资信托公司、共同基金、保险公司等机构之间的博弈，那么，两资本市场“定价权”者存在显著差异，导致了中国资本市场和美国资本市场真实投资期限存在显著差异。

其次，系统风险β与投资标度比λ的变化以参数估计的结果为中心进行波动。为了对比分析我们发现，SUR估计结果β值为1.1774， 由贝叶斯Copula估计方法所获得的结果中β在1.0至1.35的范围内以小于1的坐标点为核心进行波动。随着公司规模的增加，等高线更加密集，即规模效应放大了样本标度影响，而账面市值比的增加，其等高线趋于水平，样本标度效应对Beta值的影响在减弱，说明账面市值效应难以较大程度上影响样本标度比，即样本标度比的选取对账面市值比分布不敏感。

5 结语

经过实证研究，投资标度的存在将会影响到模型的整体特征。采用更新后的数据样本，以copula贝叶斯估计方法针对非线性FF-三因素模型进行copula 贝叶斯参数估计获得结论如下：

首先，投资标度比确实存在于新的数据样本中，该参数的作用不可忽略，相应系统风险值不能作为瞬时风险直接处理。当前数据条件下，真实投资标度明显小于投资标度观察值。由于当前市场资本流通速度明显加快，数据所获得的投资标度真实值要远小于投资标度观察值。而不同时期数据样本将对应不同的投资标度比特征。

其次，依照参数估计，我们获得了样本标度对β的差异；由于小样本数据所具有的非正态特性，我们提出了以Frank Copula函数代替传统贝叶斯模型中的正态似然函数的方法，以copula 贝叶斯估计完成数据试验。经实证研究，

对比现存美国市场数据，我国系统性风险参数beta值与投资标度gama呈现负相关关系，且程度相对较弱，投资期限趋于缩短，月数据所得样本标度比波动范围小，且其增大会减小系统风险值，即依据月度数据，我国投资者转手率较高，其真实投资期限较短，与美国年度周转率有显著差异。

其次，系统风险β与投资标度比λ的变化以参数估计的结果为中心进行波动。随着公司规模的增加，等高线更加密集，即规模效应放大了样本标度影响，而账面市值比的增加，其等高线趋于水平，样本标度效应对Beta值的影响在减弱，说明账面市值效应难以较大程度上影响样本标度比，即样本标度比的选取对账面市值比分布不敏感。

[1] Brennan M J, Zhang Yuzhao, Capital asset pricing with a stochastic horizon[R]. Working Paper. University of California, 2012.

[2] 林建浩,李幸,李欢. 中国经济政策不确定性与资产定价关系实证研究[J]. 中国管理科学,2014,22(S1):222-226.

[3] 简志宏, 李彩云. 系统性跳跃风险与贝塔系数时变特征[J]. 中国管理科学, 2013，21(03): 20-27.

[4] Longstaff F A. Temporal aggregation and the continuous-time capital asset pricing model[J]. Journal of Finance, 1989,44(4): 871-887.

[5] Lee C F, Patro D K，Liu Bo. Functional forms for performance evaluation: Evidence from closed-end country funds[M]//Lee C F，Lee A C，Lee J. Handbook of quantitative finance and risk management, 2010： 1523-1553.

[6] Handa P, Kothari S P, Wasley C. Sensitivity of multivariate tests of the capital asset-pricing model to the return measurement interval[J]. Journal of Finance, 1993, 48(4)：1543-1551.

[7] Kamara A, Korajczyk R A, Lou Xiaoxia, et al. Horizon pricing[J]. Journal of Financial and Quantitative Analysis, 2015, 51(6): 1769-1793.

[8] Darollesa S, Gourierouxb C. Conditionally fitted Sharpe performance with an application to hedge fund rating[J]. Journal of Banking & Finance, 2010, 34(3):578-593.

[9] Lina C, Liub Y. Genetic algorithms for portfolio selection problems with minimum transaction lots[J]. European Journal of Operational Research, 2008, 185(1): 393-404.

[10] Lin W T, Chen Y H. Investment horizon and beta coefficient[J]. Journal of Business Research, 1990, 21(1): 19-37.

[11] 杨宏林, 张兴全，多标度投资组合绩效度量非系统误差及校正[J]. 系统工程理论与实践, 2013, 33(9): 2187-2194.

[12] 赵宁，Lin W T，孙雪卿，基于Copula贝叶斯估计的风险值行业差异[J]. 数学的实践与认识，2015, 45(10): 17-27.

[13] 邓超, 陈学军, 基于多主体建模分析的银行间网络系统性风险研究[J]. 中国管理科学, 2016,24(01): 67-75.

[14] Darollesa S, Gourierouxb C. Conditionally fitted Sharpe performance with an application to hedge fund rating[J]. Journal of Banking & Finance, 2010,34(3): 578-593.

[15] Shih Y C, Chen S S, Lee C L, et al. The evolution of capital asset pricing models[J].Review of Quantitative Finance and Accounting 2014, 42(3): 415-448.