税率不确定性下的减记型二级资本债设计及银行最优债务结构

罗鹏飞,甘 柳,，杨招军

(1.湖南大学金融与统计学院，湖南 长沙 410079；2.南方科技大学经济与管理学院，广东 深圳 518055)

1 引言

据统计，欧洲有近半已发行的吸收经营损失型债券属于减记型债券(Write-down bond)。例如，RaboBank银行在2011年11月发行了20亿美元减记债，期限为永久性的；Barclays银行在2012年11月发行了30亿美元这种债券，期限为10年，Credit Suisse银行在2013年12月发行了25亿美元减记债，期限为10年。在中国，2013年7月22日，天津滨海农村商业银行股份有限公司发出公告，说明将发行金额不超过15亿元的10年期固定利率二级资本债券。截至2014年7月30日，另有交行、工行、中行、建行、平安银行以及重庆农商行等银行提出发行减记型二级资本工具的计划，共计3850亿元。根据上面的数据可知减记债的期限一般都是长期债务甚至是永久性的，然而，在债务期限内，税率是会发生变化的。例如，从1999-2008年历史数据来看，全球企业平均税率从31.4%减到25.9%，其中欧盟的税率从34.2%减到23.2%，亚太地区税率从31.8%减到28.4%。Alvarez等[1]实证表明税率变化频率较高且对于对于企业纳税人很难预测。税率不确定性对金融决策者而言自然是个很重要的问题。为此，本文的目标就是研究税率不确定性下的减记债设计以及银行最优债务结构。

大量文献研究的关于吸收经营损失债券类型都是或有可转债(CoCos),如国外文献Metaler和Reesor[2],Barucci和Del Viva[3-4],McDonald(2013)等[5]。在国内文献中，赵志明等[6]研究了或有可转债对企业投资与融资的影响，并未考虑另一种吸收经营损失债券——减记债。根据作者所知，研究减记债的文献很少，Himmelberg 和Tsyplakov[7]在跳模型下给出了减记债定价，研究了减记债对企业资本结构的影响。但他们只研究了减记债被发行的成因，并未给出减记债的设计，即决策者如何选取适当的减记比例。Attaoui和Poncet[8]建立债务期限模型，银行债务包括减记债和普通债，研究了债务期限结构下银行最优债务结构及减记机制。Attalui和Poncet[8]的模型没有解析地给出银行最优债务结构。再者，减记比例的设置只从银行总价值角度考虑，没有考虑金融市场的复杂性，故给予决策者的选择单一。基于此，本文考虑了金融市场摩擦--税率，解析地给出了银行债务结构，并且从银行总价值和税率效应向金融决策者选取适当的减记比例提供了灵活的方案。考虑税率不确定性对企业实物投资和融资的影响也被许多学者所青睐，例如Bohm和Funke[9],Agliardi[10],Panteghini[11-12]和Fedele等[13]。

本文的主要贡献包括：利用泊松过程来刻画税率不确定性，解析地给出了税率不确定性下银行股权价值，普通债券价值和减记债价值以及银行最优债务结构。分析了税率不确定性对银行债务结构及减记比例设置的影响。结果表明：普通债的最优券息是减记比例的凸函数，在减税情形下减少，随着减税时间点的增加而增加。减记债最优券息随着减记比例先增后减，受减税和减税时间点的影响是不确定的。此外，银行总价值和最优杠杆率随着减记比例先增后减。本文也为我国“营改增”政策的可行性提供了理论依据。同时，从银行总价值最大化和税率效应角度为金融决策者如何选择适当的减记比例提供了理论参考。

2 模型建立与假设

假设银行的资本结构包括股权，普通债及减记型二级资本债。银行产生的息税前现金流X满足几何布朗运动：

dXt=μXtdt+σXtdZt

(1)

其中μ表示现金流的期望增长率，σ表示现金流的波动率，Zt表示风险中性测度下的标准布朗运动。μ，σ是常数，本模型无风险利率为r且r>μ(保证银行资产价值有限性)。

本模型还将给出如下基本假设条件：

假设1 银行的债务结构包括普通债和减记型二级资本债。普通债的券息为Cs，减记型二级资本债的券息为Cw。一旦银行破产，普通债持有者和减记债持有者按照平等级原则分配银行剩余资产。

假设2 当银行遇到信用危机时，即无法支付债券券息Cs+Cw，此时，减记债的券息自动减少δ比例，则减记后，银行偿付的券息为Cs+(1-δ)Cw。为了分析的方便，本模型假设减记债只减记一次。

假设3 当银行现金流Xt到达Cs+Cw，减记发生，减记水平记为xw；当银行现金流Xt到达Cs+(1-δ)Cw，破产发生，破产水平记为xb。

假设4 银行破产会产生一定的资产损失，即破产损失率为α∈(0,1)。

为了刻画税率不确定对银行各证券价值及债务结构的影响，本文给出税率不确定性模型如下：

本模型假设税率服从泊松过程，给定初始税率τ0，在任何短时间dt内，税率改变为τ1的概率为λdt，因此，可得到：

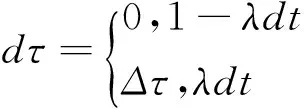
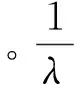
3 税率不确定性下的银行证券定价

本节将给出税率不确定下银行各未定权益的价值，本文两次采用倒向递推方法。其一，对于税率前后各未定权益价值的计算，本节先给出税率改变后的银行证券价值，此时对应的税率为τ1。然后，给出税率改变前的银行证券价值，其对应的税率为τ0。其二，对于减记前后各未定权益价值的计算，先计算减记后的价值，再计算减记前的价值。本节中，为了证券价值表述方便，上标注“a”表示减记后证券价值，上标注“b”表示减记前证券价值，下标注“1”表示税率改变后证券价值，下标注“0”表示税率改变前证券价值。

3.1 减记后银行证券价值

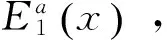
(2)

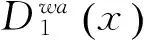
证明见附录A。

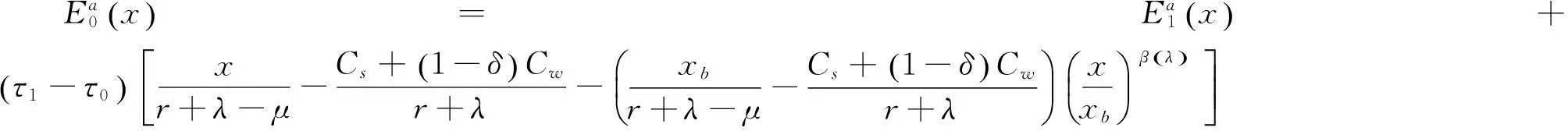
(3)

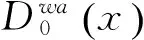
证明见附录B。

3.2 减记前银行证券价值

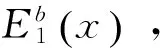
命题3.3 减记前，税率改变后银行的股权价值E1(x)为：

(4)

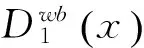
证明见附录C。

命题3.4 减记前，税率改变前银行的股权价值E0(x)为：

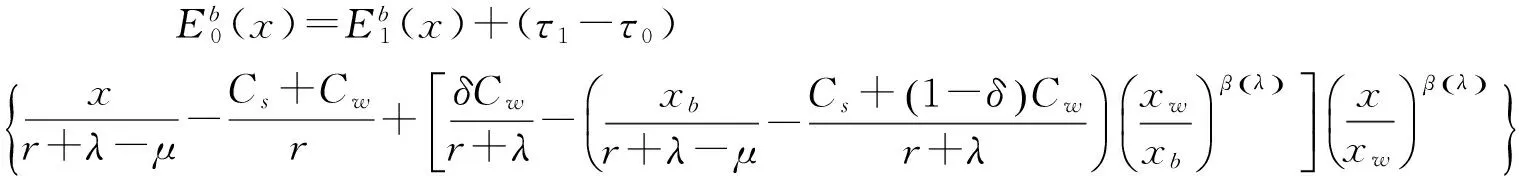
证明：与命题3.2的证明同理，可得到命题3.4的结论。

由于普通债定价不分减记前后两部分，故其定价由下述命题给出：

证明：与命题3.1，命题3.2的证明同理，可得：命题3.5的结论。

3.3 银行最优债务结构

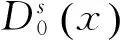
根据如上问题，可得银行最优债务结构的结论如下：

命题3.6 银行选择最优的普通债息Cs和减记债息Cw与初始现金流成比例，即Cs=Mx，Cs=Nx，且M，N满足以下代数方程组：

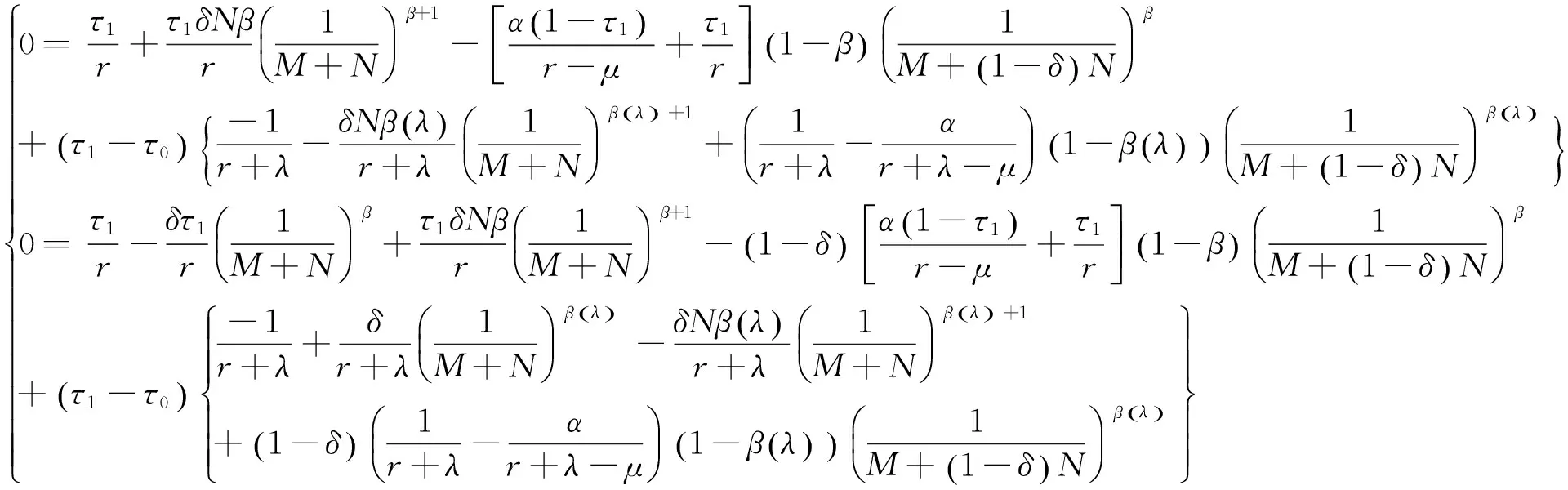
(5)

证明：v(x,Cs,Cw)分别关于Cs和Cw求导。然后，由Goldstein等[14]，可知，其券息与企业规模(企业初始现金流x)成比例。令Cs=Mx，Cs=Nx。将Cs=Mx，Cs=Nx代入两个方程即可得(5)。

4 数值比较静态分析

本节给出数值分析。若无特别说明，参见Andrikopoulos[15]，Fedele等[13]，模型参数设定如表1所示。

年轻时，潘际銮常年在外奔波，夫人和他的交流方式是“每个礼拜必须有一封信，我给他一封信，他给我一封信”，这封信，能寄出，便寄出;寄不出，便写下来，夹进日记本里。潘际銮带领团队攻克国内首个核反应堆结构焊接这一高难课题时，与世隔绝的那段日子，他们就是靠这每周一封的信件支撑。

4.1 税率变化量对银行债务结构及减记比例设计影响

通过图1和图2，可知普通债券最优券息是减记比例的凸函数，减记债最优券息随着减记比例的增加先增加后递减。图1和图2综合起来表明随着减记比例的增加，减记债占总债务的比例是递减的。这一结果是由券息两种效应所导致。在减记比例较低时，减记债比普通债更占优。一方面，减记债减记比例较小，减记后，其仍然能够带来一定的税盾效应；另一方面，减记债券息的减少能够缓解银行流动性问题，降低银行破产概率。故如图1和图2所示，在减记比例较低时，普通债的券息为令零，而减记债的券息增加。当减记比例较高时，减记债的优势有所下降。减记债的减记比例较高，一旦减记，虽然能够降低破产概率，避免无效的破产，于此同时，其券息的税盾价值也减少了。为了弥补减少的税盾价值，不增加破产概率，故如图1和图2所示，减少减记债，增加普通债券。

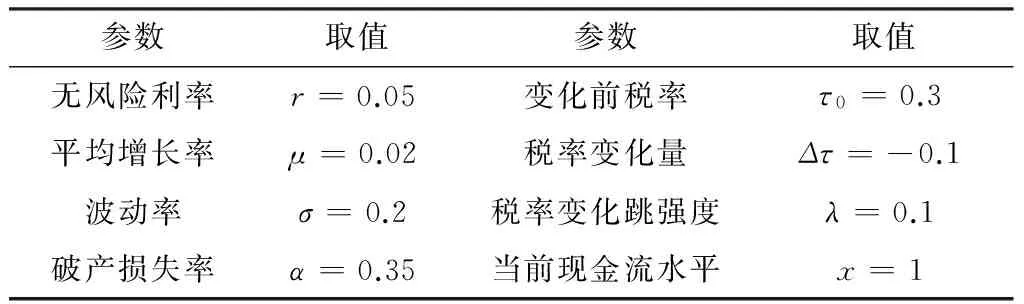
表1 基本参数

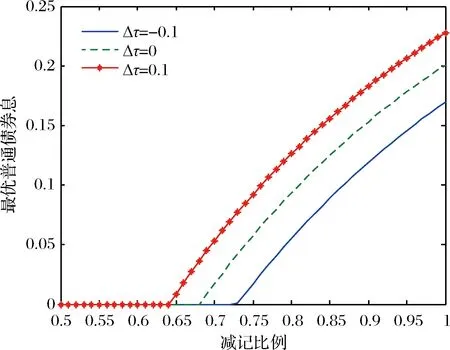
图1 最优普通债券息与减记比例及税率变化量的关系

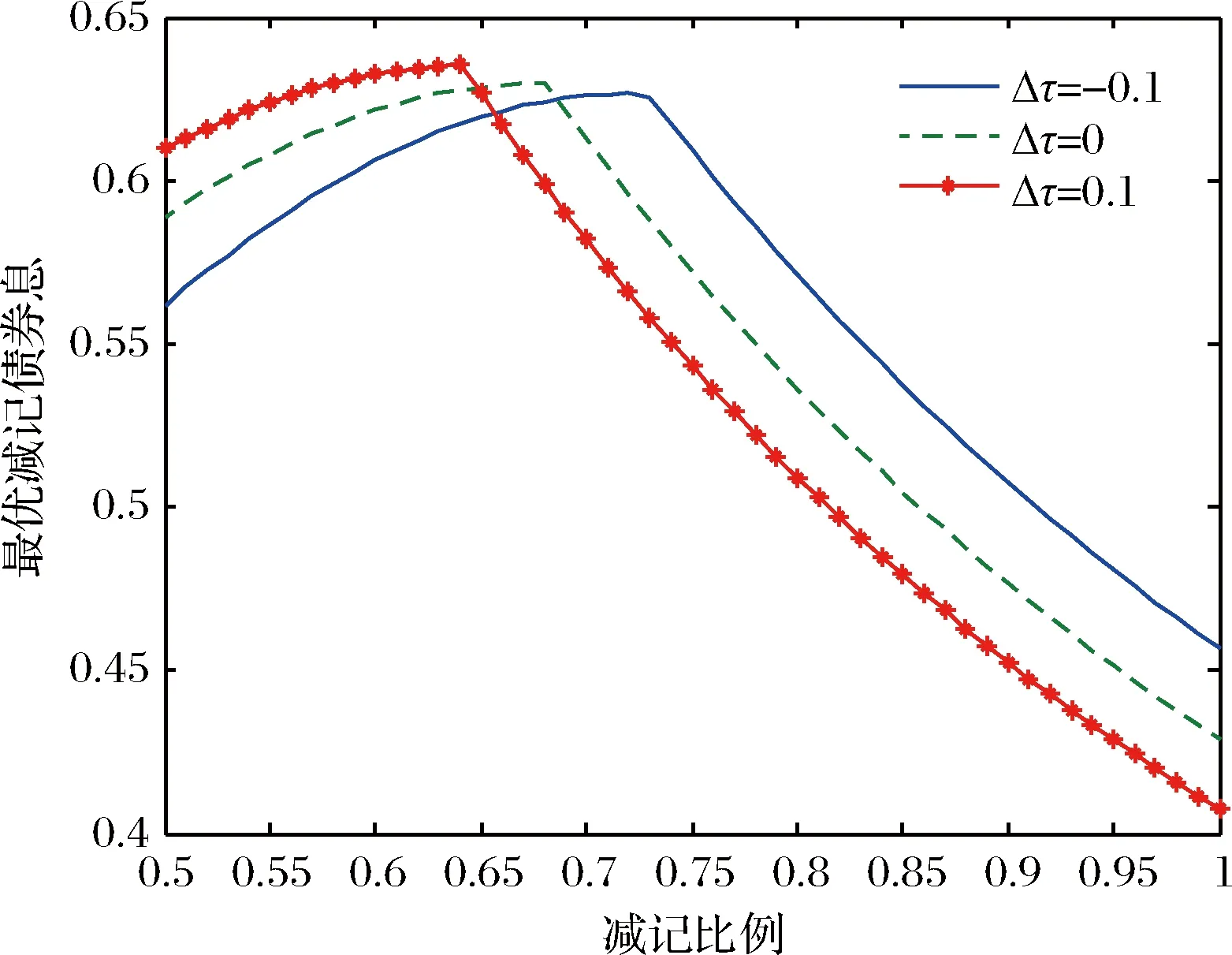
图2 最优减记债券息与减记比例及税率变化量的关系

图1也表明：普通债券最优券息随着税率变化量的增加而增加。由于普通债的避税效应比减记债占优，自然地，税率增加的提高了普通债的税盾效应。图2表明：在减记比例较低时，减记债的最优券息随着税率变化量的增加而增加；在减记比例较大时，减记债的最优券息随着税率变化量正向增加而减少。减记比例较小时，减记债既具有避税效应，又能减低破产成本，故税率量正增加导致减记债券息也增加。减记债比例较大时，减记债的税盾效应减少，当税率变化量正向增加时，为了税盾效应，银行增加了普通债券息，同时，避免增加破产成本，减少减记债的发行量。

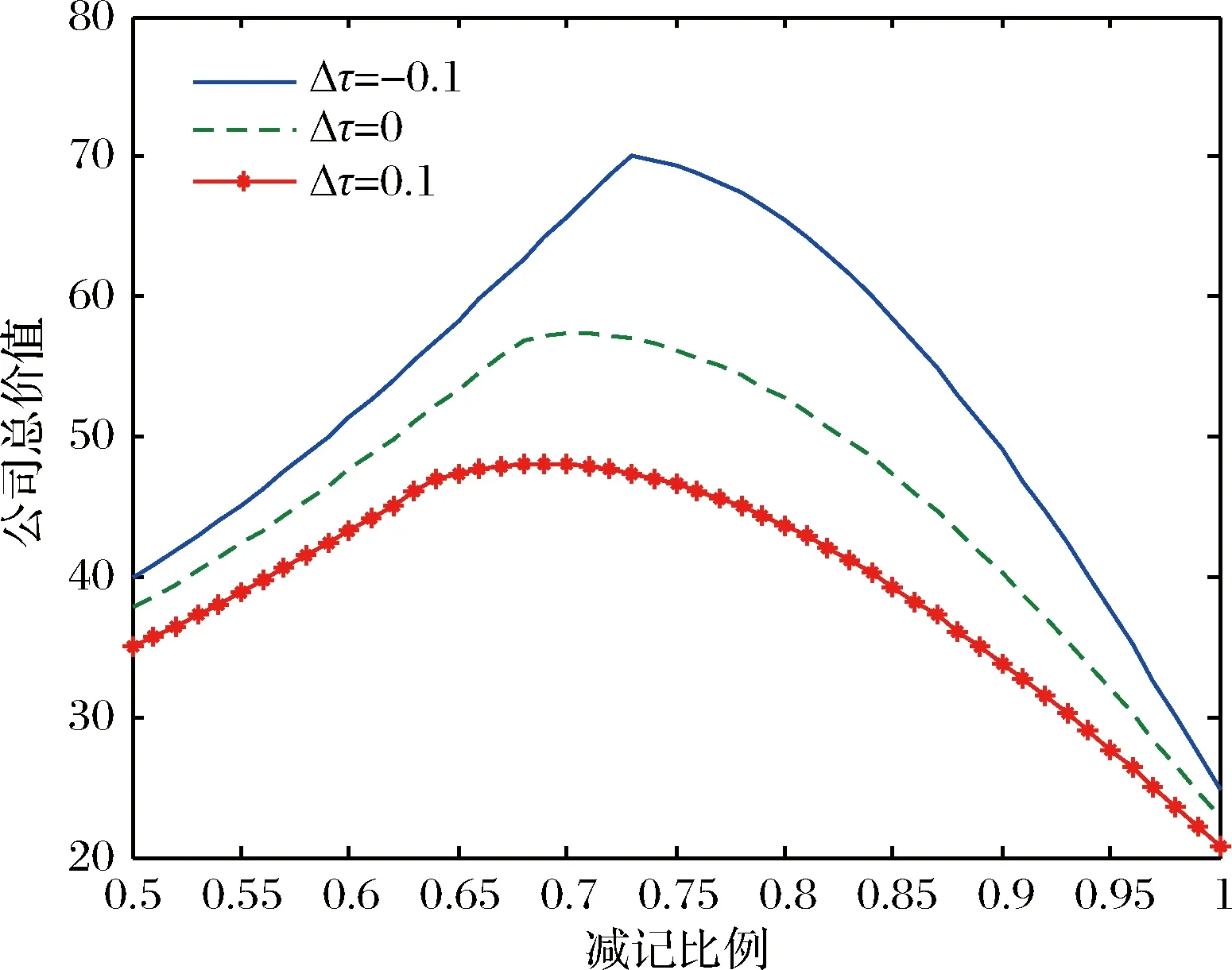
图3 银行总价值与减记比例及税率变化量的关系

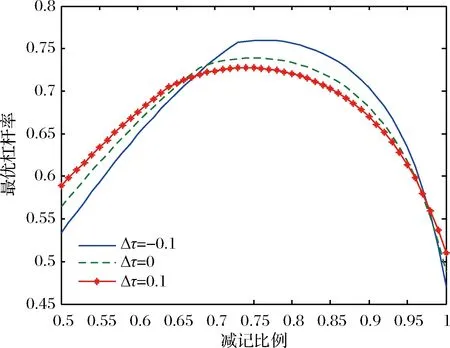
图4 最优杠杆率与减记比例及税率变化量的关系

图3表明随着减记比例的增加，银行总价值先增后减。由图1和图2，可知银行的券息发行总量几乎不受减记比例的影响，但是减记后的券息总量自然减少。一方面，当减记比例较小时，券息的破产效应使得银行总价值随着减记比例增加而增加；另一方面，当减记比例较大时，券息的税盾效应使得银行总价值随着减记比例增加而减少。由于券息的两个相反效应使得我们可以选取一个最优的减记比例，使得银行总价值最大化。这一结论在图3中很明显可以看出。图3也表明随着税率变化量正向增加，银行总价值减少。可知当税率减少时，银行总价值增加。这一结论为我国实行“营改增”政策的可行性提供了理论依据。最优减记比例随着税率变化量正向的增加而递减，这一结论如图3所示。这为金融决策者如何选取减记比例提供了理论参考。

通过图4可知银行最优杠杆随着减记比例的增加先增后减。由图1和图2可知，在减记比例较小时，券息总量增加，即债券总价值(普通债券价值与减记债价值)增加。当减记比例较大时，一旦减记，券息总量减记量大，股权价值增加，故杠杆率降低。图4也表明当减记比例较小时，税率变化量正向增加，最优杠杆率也增加。当税率变化量为负，税率减少时，银行的杠杆率减少，即减税可以起到去杠杆的作用。当减记比例较大时，税率变化量正向增加降低了杠杆率。当税率变化量为正，税率增加，银行的杠杆率减少，即增税可以起到去杠杆的作用。所以，减税和增税是否能去杠杆受到减记比例的影响，这也为金融决策者提供理论参考。例如，在减税的情形下，为了去杠杆，金融决策者应选择较小的减记比例。如果加杠杆，则选择较大的减记比例。

4.2 税率变化点的期望时间对银行债务结构及减记比例设计的影响

本小节分析税率改变点的预期时间对银行债务结构的影响，结合我国税率现状，本小节考虑减税情形，即Δτ=-0.1(增税结论与之相反)。

图5表明，减税时间点越长，普通债券的最优券息越高。由于普通债具有税盾效应优势，故减税时间点越长，发行普通债越有利。图6表明，当减记比例较小时，减税时间点越长，减记债最优券息越高。在减记比例较小时，减记债也具有普通债的优势，故解释与普通债的结论一致；当减记比例较大时，减记债不具有税盾效应优势，故减税时间点越长，减记债券息越低。

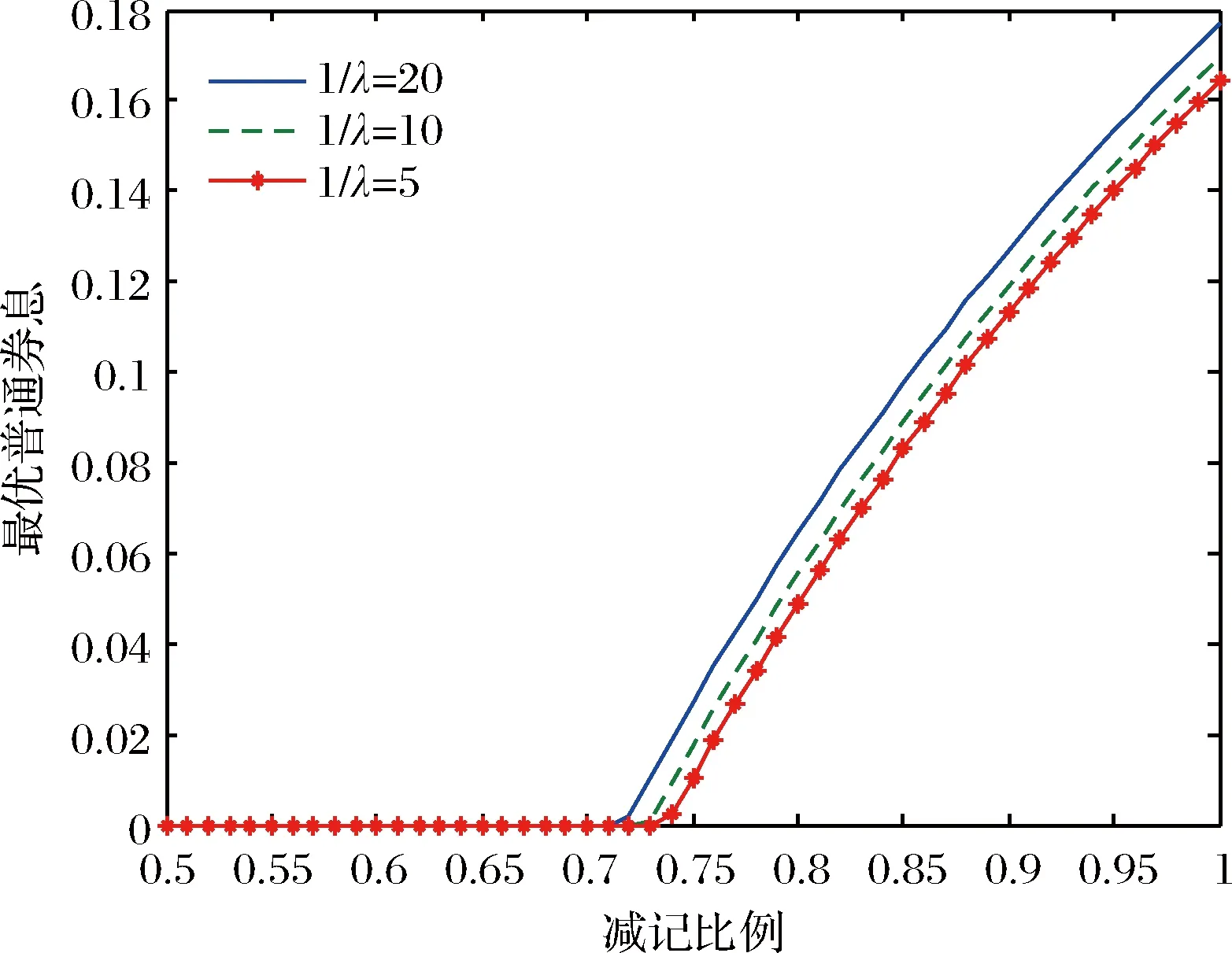
图5 最优普通债券息与减记比例及税率变化点的期望时间的关系

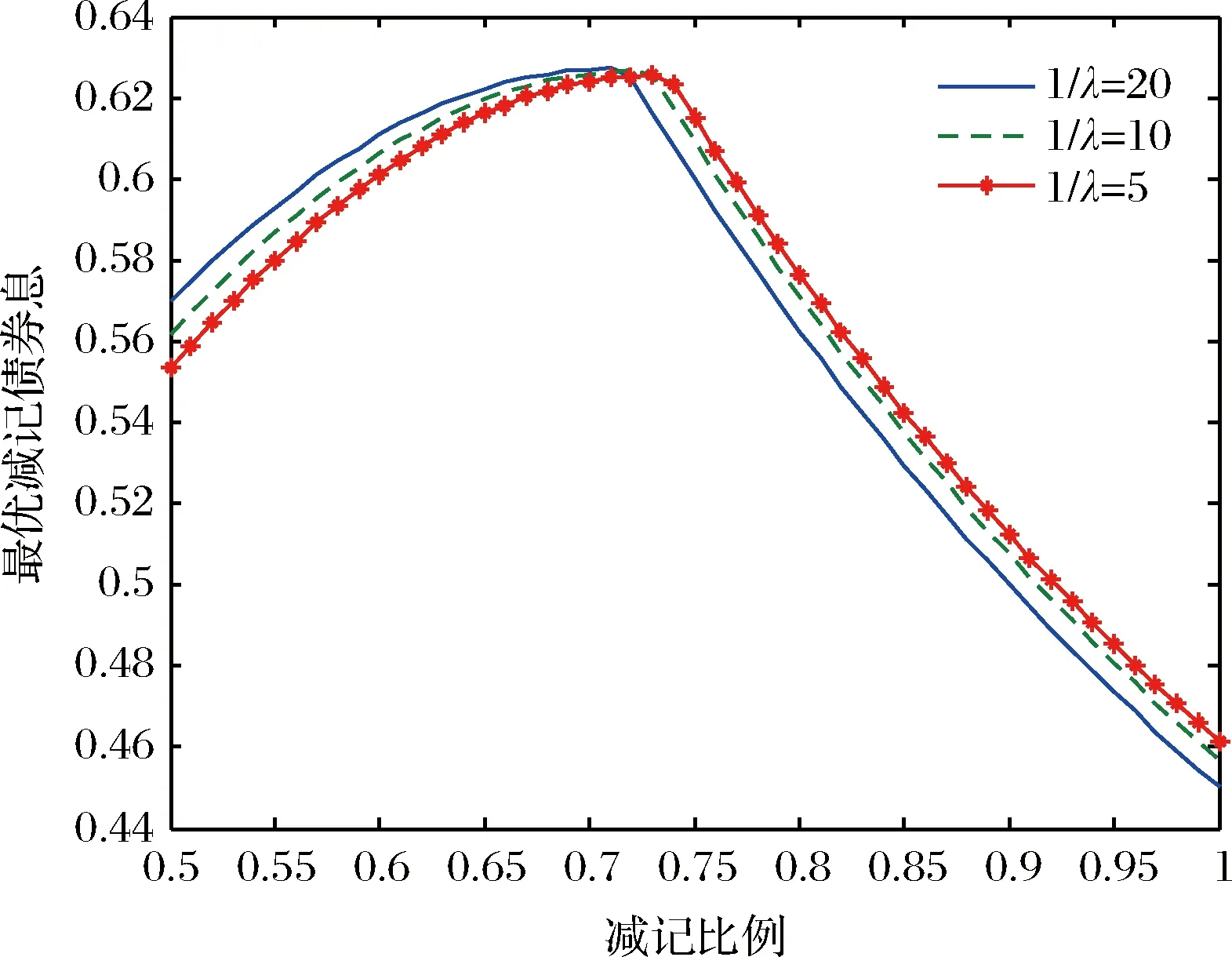
图6 最优减记债券息与减记比例及税率变化点的期望时间的关系

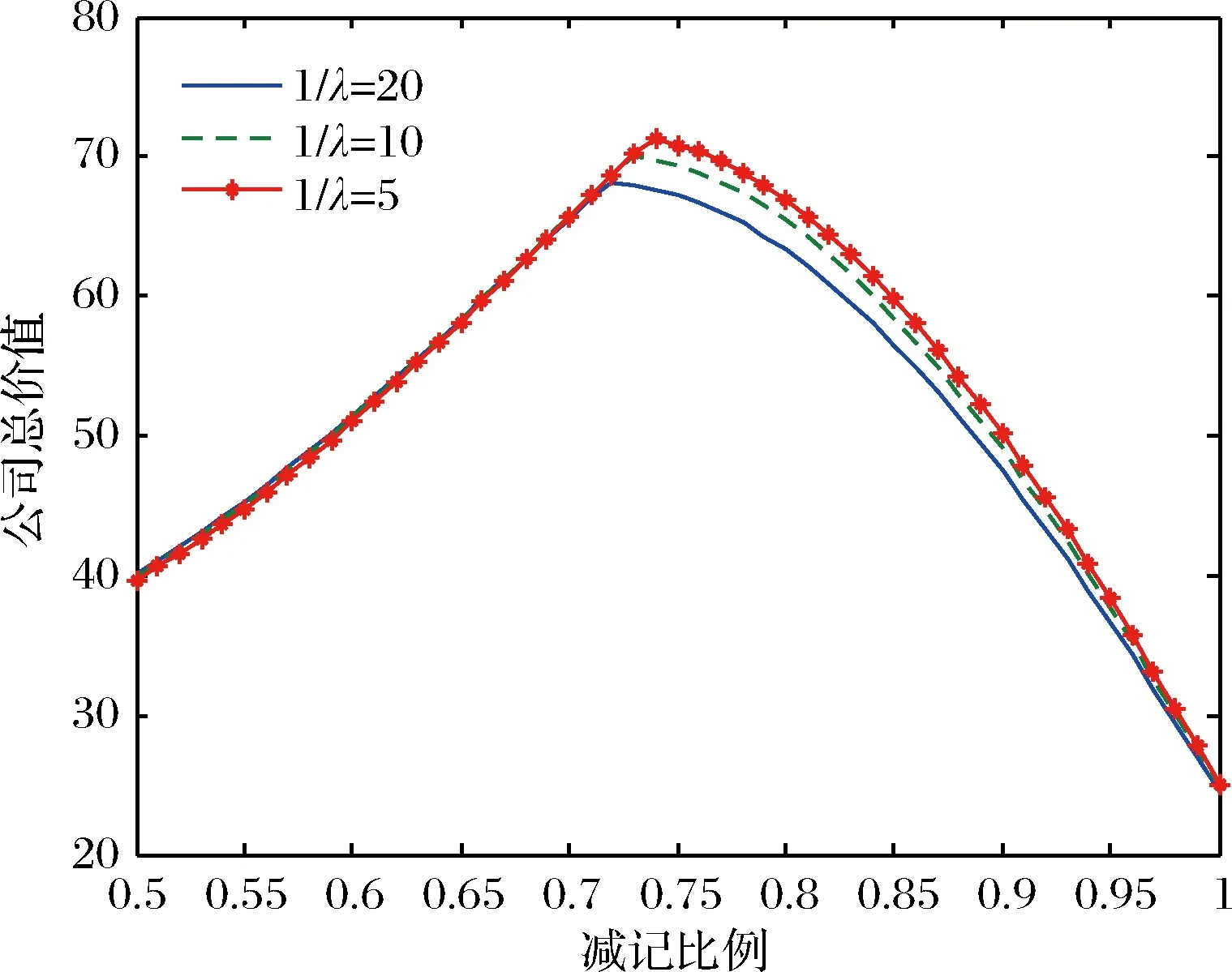
图7 银行总价值与减记比例及税率变化点的期望时间的关系

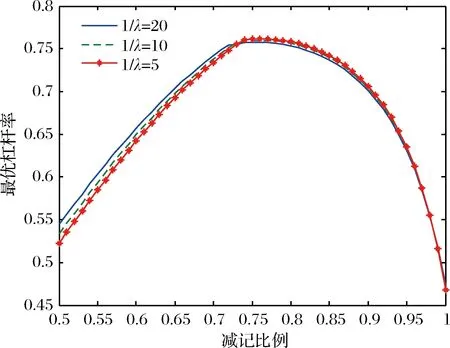
图8 最优杠杆率与减记比例及税率变化点的期望时间的关系

图7表明最优减记比例随着减税时间点的增加而递减。减税时间点越长，减记比例越小，则税盾收益越大。减税时间点越长，银行总价值越低。这是因为减税时间点长，减记债最优券息减少，而普通债券增加，此时，券息破产效应占主导，故银行价值降低。通过图8可知减税时间点越长，银行杠杆率越高。这是因为减税时间点越长，避税效应导致债务的发行量增加，从而提高了杠杆率。

5 结语

本文建立了税率不确定性下的银行证券定价模型，分析了税率不确定性对银行债务结构及减记债设计的影响。一方面，本文为我国“营改增”政策的可行性提供了理论依据。另一方面，本文从银行总价值最大化和税率效应角度为金融决策者如何选择适当的减记比例提供理论参考。如：从银行总价值最大化角度考虑，决策者应选取较大的减记比例；从税率效应角度，当处于减税情形，如果决策者想去杠杆，则应选取较小的减记比例，如果想加杠杆，则应选取较大的减记比例，当处于增税情形，则反向选取即可。

本模型只适合减记发生一次的情况，实际情况中，银行可能处于某种因素考虑(如税盾效应)，减记债减记的次数为有限次数。在这种情况下，金融决策者如何动态设计减记比例，这是本文下一步可研究的问题。其次，本模型假设在破产时刻，普通债券人和减记债权人根据平等原则获得企业剩余价值。这一假设条件限制了分析实际情况中其他债务优先原则对减记债设计的影响。因此，债务优先原则对减记债设计的影响也可作为本文另一个拓展问题研究。

附录A 命题3.1的证明

利用伊藤引理，可得：

(6)

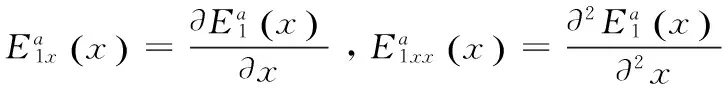
(6)式的解为:

(7)

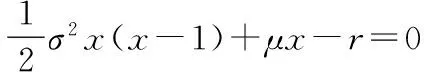
附录B 命题3.2的证明

利用伊藤引理，可得：

(8)

将(6)代入(8)，整理，可得：

(9)

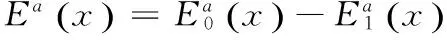
(9)式的解为：

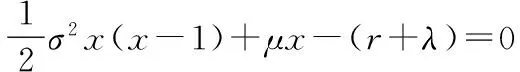
(10)

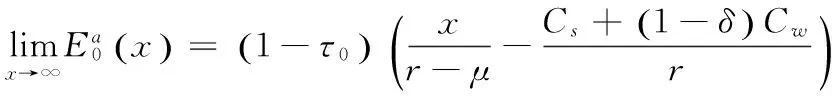
附录C 命题3.3的证明

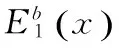
(11)

(11)式解为：

(12)

[1] Alvarez L H R, Kanniainen V, Södersten J. Tax policy uncertainty and corporate investment: A theory of tax-induced investment spurts [J]. Journal of Public Economics, 1998, 69(1): 17-48.

[2] Metzeler A, Reeser R M. Valuation of contingent capital bonds in Merton-type structural models [R]. Working Paper University of Western Onatio, 2011.

[3] Barucci E, Del Viva L. Countercyclical contingent capital [J]. Journal of Banking & Finance, 2012, 36(6): 1688-1709.

[4] Barucci E, Del Viva L. Dynamic capital structure and the contingent capital option [J]. Annals of Finance, 2013, 9(3): 337-364.

[5] McDonald R L. Contingent capital with a dual price trigger [J]. Journal of Financial Stability, 2013, 9(2): 230-241.

[6] 赵志明, 杨招军, 王淼. 基于或有可转换证券的投资和融资决策[J]. 中国管理科学, 2016, 24 (7): 18-26.

[7] Himmelberg C P, Tsyplakov S. Incentive effects of contingent capital[R]. Working Paper University of South Carolina, 2012.

[8] Attaoui S, Poncet P. Write-down bonds and capital and debt structures[J]. Journal of Corporate Finance, 2015, 35: 97-119.

[9] Boehm H, Funke M. Optimal investment strategies under demand and tax policy uncertainty[J]. Working paper,cEsifo Group Munich，2000.

[10] Agliardi E. Taxation and investment decisions: a real options approach [J]. Australian Economic Papers, 2001, 40(1): 44-55.

[11] Panteghini P. On corporate tax asymmetries and neutrality [J]. German Economic Review, 2001, 2(3): 269-286.

[12] Panteghini P M. Corporate tax asymmetries under investment irreversibility [J]. FinanzArchiv: Public Finance Analysis, 2002, 58(3): 207-226.

[13] Fedele A, Panteghini P M, Vergalli S. Optimal investment and financial strategies under tax-rate uncertainty [J]. German Economic Review, 2011, 12(4): 438-468.

[14] Goldstein R, Ju Nengju, Leland H. An EBIT‐based model of dynamic capital structure[J]. The Journal of Business, 2001, 74(4): 483-512.

[15] Andrikopoulos A. Irreversible investment, managerial discretion and optimal capital structure [J]. Journal of Banking & Finance, 2009, 33(4): 709-718.