多国股票市场的高频波动相关性研究
2018-03-09罗嘉雯陈浪南
罗嘉雯,陈浪南
(1.华南理工大学工商管理学院,广东 广州 510640; 2.中山大学岭南学院,广东 广州 510275)
1 引言
经济全球化已经成为世界经济发展的主要趋势,而金融国际化是经济全球化中重要的一个方面。金融国际化的发展有利于资本和产品的全球性流动,提高金融市场的运行效率。但与此同时,金融国际化也增强了国与国之间的风险传递,加剧了全球金融市场的波动。此外,随着投资于多国金融市场的产品不断增加,如何制定正确的跨国投资策略得到广泛关注。因此,准确地衡量多国金融市场的波动相关性(联动结构)有助于防范全球性的金融风险,保护投资者权益,且对跨国资产定价和投资组合选择起着重要的作用。
传统文献对跨国股票市场的波动相关性的研究大多基于Bollerslev[1]提出的MGARCH 模型进行建模研究。MGARCH 模型通过设定不变的条件相关性把单变量GARCH模型拓展为多变量GARCH模型。基于MGARCH框架下的模型拓展包括双变量的BEKK-GARCH模型[2]和具有时变相关性的DCC-GARCH模型[3]。Bauwens等[4]对具有MGARCH结构一类模型做了详细的文献回顾。

在现有研究基础上,本文运用多个国家股票市场的高频日内交易数据,结合多元HAR(MHAR)模型和Jin Xin和Maheu[16]提出的带马尔科夫机制转换结构的MGARCH模型,并通过Engle[3]提出的DCC-GARCH模型结构降低多变量MGARCH结构的参数维度,提出了带马尔科夫状态转换结构的MS-MHAR-DCC模型。同时,考虑金融时间序列尖峰厚尾特征,本文进一步假设MHAR模型残差服从t分布,建立MS-MHAR-DCC-t模型。本文通过Vrugt等[17]提出的多链抽样方法DREAM算法替代传统的随机游走的M-H抽样方法加快MCMC抽样估计的收敛速度。
2 模型的构建和估计
2.1 模型的构建
本文运用多个发达股票市场的高频日内交易数据,对跨国股票市场的高频波动相关性进行研究。考虑到不同国家所处时区不同造成的非同步交易问题,本文假设各股票市场的非交易时间内的信息可以由过夜收益率捕捉。
(1)
其中,ρ是系数,通过系数把基于交易时间内收益序列计算的RV拓展为基于24小时所有交易信息的过夜RV。系数ρ的计算方法如下:
(2)

已实现波动率的计算方法为:
(3)
其中,δ为日收益率的抽样频率。rt通过日内对数收益计算,rt=100×(logPt-logPt-δ)。在计算已实现波动率时,本文先通过Barndorff-Nielsen等[20]的高频数据处理方法先对数据进行预处理,消除每日交易数据过少的异常点。
同时,考虑到模型截断点的影响,本文结合Corsi等[21]提出的高频波动率预测模型——HAR模型和Jin Xin和Maheu[16]提出的具有马尔科夫状态转换结构的贝叶斯MGARCH-B模型,并通过Engle[3]的多变量波动率DCC-GARCH结构降低模型参数维度,建立MS-MHAR-DCC模型和MS-MHAR-DCC-t模型。模型形式为:
wt~NID(0,I)
(4)
其中,

Ht=DtRtDt
(5)
Dt=diag(σk,t)
(6)
(7)
Rt=diag(Ct)-1/2Ctdiag(Ct)-1/2
(8)
(9)


(10)


2.2 模型参数的估计
本文通过贝叶斯推导的方法对模型参数进行估计。定义模型的位置参数集为Ψ={S,π1,π2,Θ,Φ,Ht,Λt},其中Φ={β0,β1,β2,β3}和Θ={ω1,…,ωk,κ1,…,κk,λ1,…,λk,a,b}。本文把所有参数分成7个参数块,通过MCMC方法对根据设定的参数块的后验条件分布进行联合抽样。块抽样的后验分布为:
1.p(S|Π,Θ,Φ,RV);
2.p(πi|S);
3.p(Θ|S,Φ,RV);
4.p(Λ|Θ,Φ,S,RV);

6.p(Φ|Λ,S,RV,d)
7.p(d|ut)
2.3 M-H抽样法和DREAM抽样法
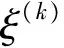

对于第3步和第6步,分别是对DCC-GARCH结构和MHAR结构内的参数进行抽样,由于块抽样的参数较多,本文主要采取Vrugt等[17]提出的DREAM算法对参数进行抽样。在DREAM方法下,多条马尔科夫链可以平行运行,以实现对参数最优值的搜索,每一条链中新一次抽样的中心值和方差可以基于其他链的信息进行自动调整。此外,参数块Θ和Φ中的元素可以以1-CR的概率进行抽样更新,CR是交互概率,这样就不需要在每次抽样中对参数块中所有的参数进行同时接受或同时拒绝,而是随机选取参数块中的一个参数子集进行同时更新,从而加快收敛速度。

第一步,根据其他链的位置决定提议值Zi
(11)

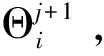
(12)
根据Vrugt[17],在运用DREAM抽样方法时,对于每次的MCMC迭代,通过计算每条MCMC链的对数似然函数值并对其进行分位,可以认为对数似然函数值小于第三分位点和第二分位点之差的MCMC链为异常链,在预烧期间,通过把异常的MCMC链置换为具有最高对数似然函数值的MCMC链可以加快参数的收敛过程。
3 数据与变量
本文采用日本、香港、新加坡、英国、欧洲和美国股票市场的主要指数的5分钟高频数据对这六个国家股票市场收益的共同波动关系进行研究。本文的样本包括美国标普500 指数(SPI)、英国富时 100指数(FTI)、欧洲斯托克50指数(EUI)、日经225指数(NEI)、新加坡海峡时报指数(STI)和香港恒生指数(HIS),样本期涵盖2010年1月1日至2013年12月31日一共4年的时间区间,数据来源为TICK数据库。这六个股票市场具有不同的交易时间,以格林威治时间(GMT)来定义,日经225指数指数的交易时间为0:00至7:00 GMT,香港恒生指数的交易时间为2:00至 8:00 GMT,新加坡海峡时报指数交易时间为1:00至 9:00 GMT,英国富时100指数和欧洲斯托克50指数的交易时间为7:00/8:00至15:30/16:30 GMT,美国标普500指数的交易时间为13:30/14:30至 20:00/21:00 GMT。通过运用过夜已实现波动率,本文把基于交易时间内收益序列计算的已实现波动率拓展为基于24小时所有交易信息的过夜已实现波动率,从而解决因为交易时间不同而导致的非同步交易问题。
根据Barndorff-Nielsen等[22]提供的对高频金融数据处理的基本步骤,本文运用相似的步骤对高频数据进行整理:(1)删除交易时间以外的样本;(2)删除日内样本少于正常交易日80%的样本量的交易日样本;(3)删除每个时点上重复出现的价格;(4)删除少于3个股票市场交易的多国(区)公共假期,如圣诞节,新年和复活节。在对数据进行处理之后,本文利用每个股票市场的日内数据计算每日的过夜已实现波动率,在进行多个股票市场的波动率序列匹配后,得到一个包含1027个交易日的样本。
表1显示六个股票指数日内平均收益和已实现波动率的基础统计分析。如表一所示,在6个股票指数之中,新加坡股票市场具有最低的平均波动率(0.3045),而欧洲股票市场的平均波动率最高(1.3714)。日本股票市场具有最高的平均日内股票收益率(0.0008),而新加坡市场具有最低的平均日内股票收益率(0.0001)。所有序列都表现出显著的金融时间序列的尖峰厚尾特征,因此本文考虑结合t分布进行建模,从而有效拟合高频金融时间序列的尖峰厚尾特征。
表1的最后一行显示出过夜已实现波动率的系数,通过系数和交易时间内已实现波动的乘积可以获得过夜已实现波动率。其中,英国股票市场的过夜已实现波动率系数最大(2.495),表示英国股票市场的隔夜平均波动最为剧烈,即受到其他国家股票市场的信息溢出的影响最大。而美国股票市场的过夜已实现波动率系数最小(1.3516),代表美国股票市场的隔夜波动较小,表现出美国股票市场对其他国家股票市场的信息传递较为不敏感,也进一步表现出美国作为经济金融巨头在全球信息传递中的引导作用。
图1和图2分别显示6个股票指数的日内平均收益和已实现波动率的时间趋势图。根据图1和图2,6个股票指数的日内平均收益和已实现波动率都显示出相似的变化趋势,在特定时期都显示出高收益和高波动的特征,如2010年5月,对应美国批准金融监管改革法案,迫使美国金融公司做出重大调整;2011年7-12月,对应欧债危机的爆发和希腊援助计划的公投,导致全球股票产生巨大波动;2012年8-10月,对应英国监管部门对伦敦银行间同业拆借利率(LIBOR)的彻底改革以及大幅削减其制定的利率数量。2013年6-7月,对应美联储在QE退出问题上举棋不定以及欧洲央行降息促进经济发展。由此可见,由于外部经济危机和政策变化,往往造成国际股票市场间的波动相关性发生截断性变化,因此,本文进一步结合马尔科夫机制转换结构进行建模。

表1 变量的统计分析
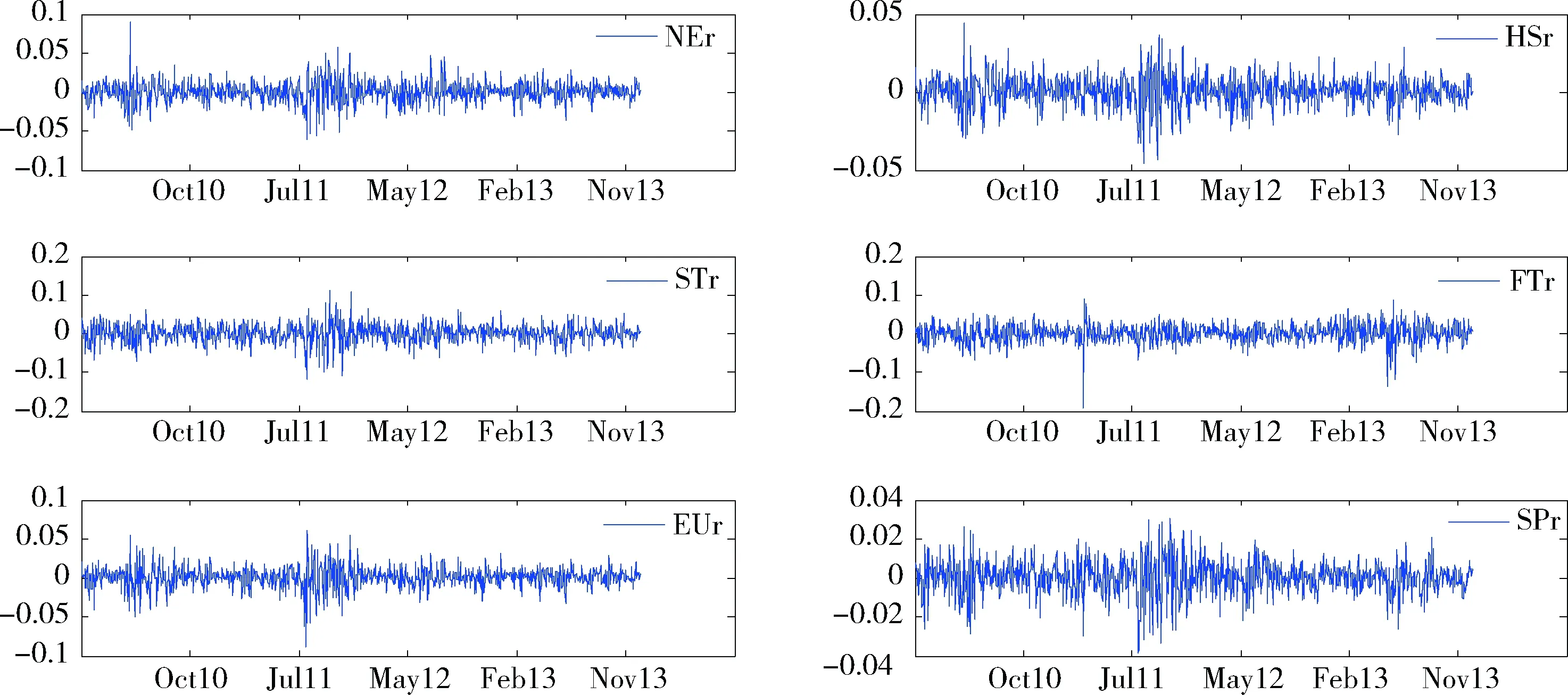
图1 6个股票指数的日内收益时间趋势图注:NEr, HSr, STr, FTr, EUr和SPr表示日本Nikkei 225指数(NEI)、香港恒生指数(HSI),新加坡海峡时报指数(STI)、英国FTSE 100指数(FTI)、欧洲STOXX 50指数(EUI)和美国S&P 500 指数(SPI)的日内平均收益(下同)。

图2 6个股票指数的过夜已实现波动率时间趋势图
4 实证结果与分析
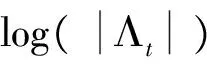

图3 MS-MHAR-DCC 模型状态变量和log(|Λt|)的后验均值

图4 MS-MHAR-DCC-t 模型状态变量和log(|Λt|)的后验均值

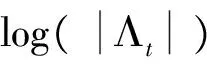

图5 log(|Ht|)和log(|Vt|)的后验均值
图6和图7显示基于MS-MHAR-DCC模型和MS-MHAR-DCC-t模型建模的6个股票市场波动的动态相关性,即(5)-(9)DCC-GARCH结构中的相关性矩阵Rt不包含对角元的下三角元素,共有15对市场波动的动态相关性。从图6和图7来看,MS-MHAR-DCC模型和MS-MHAR-DCC-t模型下股票市场间波动的动态相关性的数值大小类似,所有市场的波动相关性在大部分时期都表现为正相关。其中相同地域的股票市场,如亚洲股票市场(日本股票市场、香港股票市场和新加坡市场)和欧洲市场(英国市场和欧洲市场)之间波动表现出较强的动态相关性,美国股票和其余5个国家股票市场波动的动态相关性在大部分时期都表现较强的正相关,表现出美国作为全球经济金融巨头在世界金融市场的波动引导作用。MS-MHAR-DCC-t模型的动态相关性曲线相比MS-MHAR-DCC模型更为平滑,主要原因是MS-MHAR-DCC-t模型的动态相关性具有更明显的长记忆性特征(根据波动率矩阵和相关矩阵的长记忆性特征的κi+λi,i=1,…,6和a+b的估计结果,MS-MHAR-DCC-t模型中的估计值相对于MS-MHAR-DCC模型中的估计值更接近于1),因此动态相关性随时间的变化趋势较为平缓。
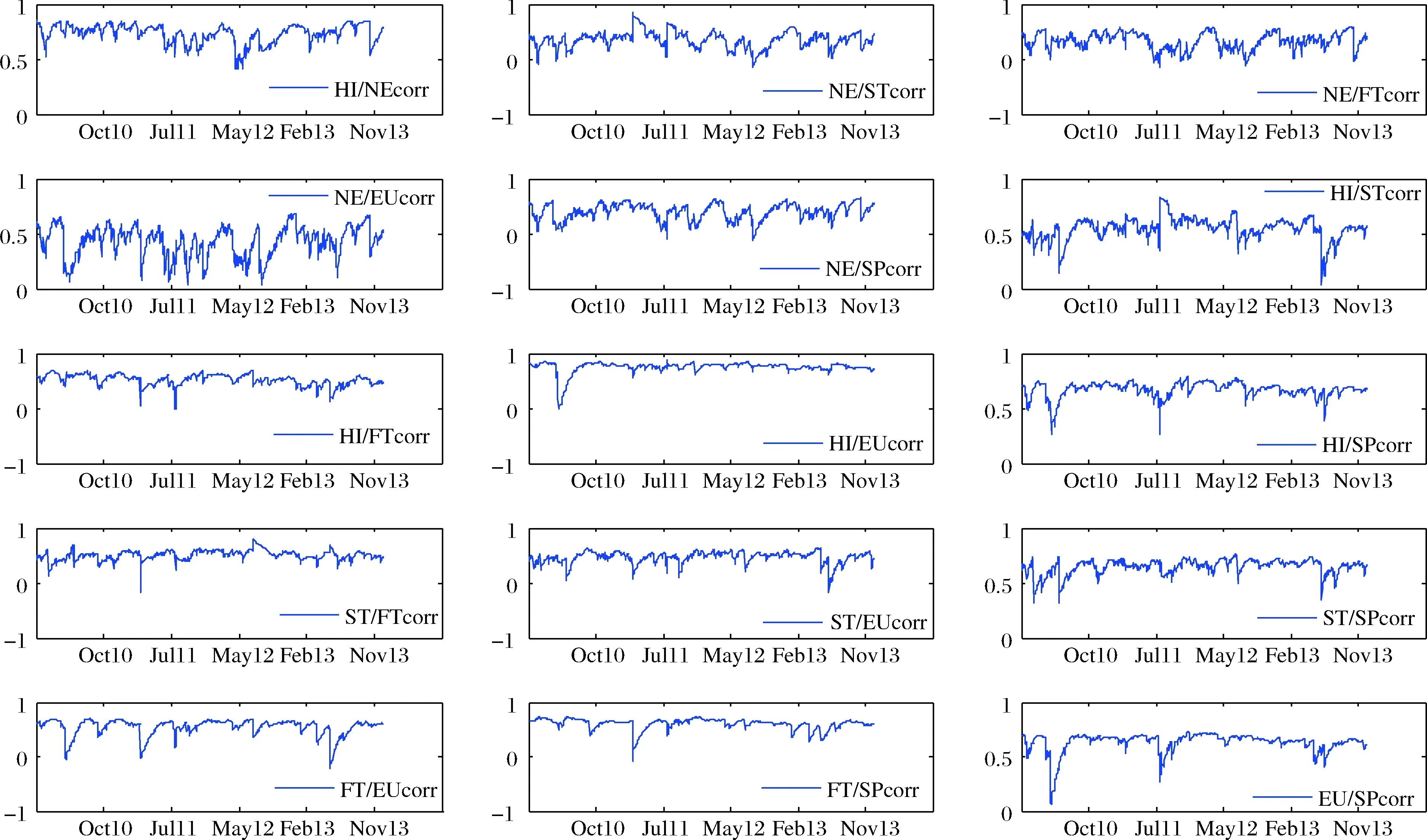
图6 MS-MHAR-DCC模型下股票市场动态相关性的后验均值

图7 MS-MHAR-DCC-t模型下股票市场动态相关性的后验均值
5 结语
考虑结构断点对多变量波动率建模的影响,本文结合具有马尔科夫机制转换结构的DCC-GARCH模型和向量化的HAR模型建立了高频多变量波动率模型MS-MHAR-DCC模型。考虑金融时间序列的尖峰厚尾特征,本文进一步假设MHAR模型残差服从student-t分布,建立MS-MHAR-DCC-t模型。本文运用新建立模型并采用美国、英国、欧盟、日本、新加坡和香港的股票市场的数据,探讨不同国家(地区)股票市场收益波动的关联性。由于不同国家(地区)的股票市场存在交易非同步性,本文通过过夜已实现波动率对非同步交易数据进行处理。同时,本文通过Vrugt等[18]提出的DREAM算法替代传统的RWMH抽样方法加快MCMC抽样估计的收敛速度。
实证结果显示:(1)从过夜已实现波动率的系数来看,美国的隔夜股票市场受到外来信息冲击的影响最小而英国的隔夜股票市场受到外来信息冲击的影响最大。(2)通过引入带马尔科夫结构的外部随机矩阵,可以有效识别金融市场间动态波动相关性的结构断点;且相比MS-MHAR-DCC-t模型,MS-MHAR-DCC模型识别到的截断状态更多,且持续时间更长。(3)模型的截断时期内,6个市场的波动相关性受到正向冲击为主,即在截断时期内国际股票市场的波动相关性相比平常状态更大。(4)多国股票市场波动相关性较大的时期恰好对应高波动率的时期,表明在市场较为动荡的时期,各股票市场间的波动相关性也就会增大,市场间波动的溢出效应也随之增强。(5) 相同地域的市场,如亚洲股票市场(日本股票市场、香港股票市场和新加坡市场)和欧洲市场(英国市场和欧洲市场)的动态波动相关性在大部分时期内表现为较强的正相关。(6)美国股票和其余5个国家股票市场波动的动态相关性在大部分时期都表现为较强的正相关,表现出美国作为全球巨头在世界金融市场波动的引导作用。
[1] Bollerslev T. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized arch model[J].Review of Economics & Statistics, 1990,72(3):498-505.
[2] Engle R F, Kroner K F. Multivariate simultaneous generalized ARCH[J]. Econometric theory,1995,11(01): 122-150.
[3] Engle R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models[J].Journal of Business & Economic Statistics, 2002, 20(3): 339-350.
[4] Bauwens L, Laurent S, Rombouts J V. Multivariate GARCH models: A survey[J]. Journal of Applied Econometrics,2006, 21(1): 79-109.
[5] Bekaert G, Hodrick R J, Zhang, Xiaoyan. International stock return comovements[J]. The Journal of Finance,64(6): 2591-2626.
[6] Beine M, Cosma A, Vermeulen R. The dark side of global integration: Increasing tail dependence[J]. Journal of Banking & Finance, 2010, 34(1): 184-192.
[7] Rapach D E, Strauss J K, Zhou G. International stock return predictability: What is the role of the United States?[J]. Journal of Finance, 2013, 68(4): 1633-1662.
[10] 刘晓星, 段斌, 谢福座. 股票市场风险溢出效应研究:基于EVT-Copula-CoVaR模型的分析[J] . 世界经济, 2011,(11):145-159.
[11] 熊正德, 文慧, 凌语蓉. 基于时频分析的农产品期货市场与外汇市场联动关系研究[J].中国管理科学, 2013,21(S1):255-263.
[12] 熊正德, 文慧, 熊一鹏. 我国外汇市场与股票市场间波动溢出效应实证研究——基于小波多分辨的多元BEKK-GARCH(1,1)模型分析[J].中国管理科学, 2015, 23(4):30-38.
[13] 王璐. 国际多元化下多维金融市场相关结构测度——以金砖国家新兴市场为对象[J]. 数理统计与管理, 2015,(3):498-512.
[14] 王鹏,魏宇,王建琼. 不同矩属性波动模型对中国股市波动率的预测精度分析[J].数理统计与管理,2010, 29(3):550-559.
[15] 何德旭, 苗文龙. 国际金融市场波动溢出效应与动态相关性[J].数量经济技术经济研究, 2015,(11):23-40.
[16] 夏南新. 国际金融市场波动非线性因果性和溢出效应[J].管理科学学报, 2016, 19(3):64-76.
[17] Jin Xin, Maheu J M. Modeling covariance breakdowns in multivariate GARCH[J]. Journal of Econometrics, 2016,194(1): 1-23.
[18] Vrugt J A, TerBraak C J F, Diks C G H, et al. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling[J].International Journal of Nonlinear Sciences and Numerical Simulation, 2009, 10(3): 273-290.
[19] Ahoniemi K, Lanne M. Overnight stock returns and realized volatility[J]. International Journal of Forecasting, 2005, 29(4): 592-604.
[20] Koopman S J, Jungbacker B, Hol E. Forecasting daily variability of the S&P 100 stock index using historical, realised and implied volatility measurements[J]. Journal of Empirical Finance, 2005, 12(3): 445-475.
[21] Martens M, Poon S H. Returns synchronization and daily correlation dynamics between international stock markets[J]. Journal of Banking & Finance, 2001, 25(10): 1805-1827.
[22] Barndorff-Nielsen O E, Hansen P R, Lunde A,et al. Realized kernels in practice: trades and quotes[J].The Econometrics Journal, 2009, 12(3): C1-C32.
[23] Corsi F. A simple approximate long-memory model of realized volatility[J]. Journal of Financial Econometrics, 2009, 7(2): 174-196.
[24] Gelman A, Rubin D B. Inference from iterative simulation using multiple sequences[J]. Statistical Science, 1992, 7(4): 457-472.
