基于混合分布的中国股票波动风险因素的识别与分析

王安兴,谭鲜明

(1上海财经大学金融学院，上海 200433；2.加拿大麦吉尔大学健康中心，加拿大 魁北克 H4A 3J1)

1 引言

金融研究中，习惯用证券的收益或收益率代表证券，证券的预期收益(收益的均值)与证券的波动率(收益率的标准差)是描述收益的两个重要基本量。股票收益可以用多因素模型表示[1-3]，著名的多因素模型是五因素模型[1-2]。五因素模型说明影响股票预期收益的共同因素个数是五个，有大量文献研究股票收益率的多因素模型。

股票波动率是测量股票风险的重要指标，在资产定价、金融风险管理中有重要应用。GARCH模型可以很好的描述股票波动集聚性[4～6]，日内新的信息不断到达，且信息数量序列相关，导致股票价格变化出现集聚性现象，产生GARCH效应[7],市场深度与信息到达的相关性与市场波动率特性有关[8]。因为波动率在测量股票风险中有重要作用，高频数据情况下的金融资产收益率已实现波动率的估计问题时，可以通过混合泊松分布而非传统的连续扩散模型来描述价格过程[9]，利用SV-t模型来拟合金融时序的边缘分布可以帮助解决非线性相关的高维投资组合风险度量问题[10]。

如果根据多因素模型计算股票收益率的方差，可以很容易发现，决定股票波动率(波动)的共同影响因素也是有限个。分析或识别股票波动的共同因素个数的文献却不多见。

识别股票波动率的共同影响因素个数，也就是分析股票波动率来自多少个组或者类。聚类是将物理或抽象对象的集合分组成为由类似的对象组成的多个类的过程。同一个类中的对象有很大的相似性，而不同类间的对象有很大的相异性。混合分布(Finite mixture distribution)或混合模型(Finite mixture model)是常用于基于模型的聚类分析(Model-based clustering)的重要模型[11-12]，对来自不同总体的样本，混合分布推断每个样本来自不同总体的概率。

混合模型被广泛应用于医学及其他学科研究中[13]，例如，应用正态混合模型分析新生儿癫痫的分类与预测[14]，以及分析医学图像[15]。

应用混合分布研究股票价格行为也是文献研究的热点之一。GARCH效应产生的原因是日内信息流到达的数量序列相关。基于不同的信息对股票价格的波动性影响不同，单个股票收益率与成交量时间序列视为来自不同分布的样本，用混合分布建立股票价格波动率和成交量的关系[7]，用混合分布解释股票价格波动的持续性[16-17]。由于混合分布对股票价格波动持续性的解释有限[17-21]，股票价格波动性和成交量的双变量混合模型被提出[22]。混合分布也可以应用于单因子模型的定价问题[23]。

由于影响所有股票价格的公开的公共信息数量有限，影响所有股票波动率的共同因素也有限。例如股票的5因素模型提示影响股票波动率的共同因素可能不超过5个。然而，在现有的文献中，没有看到解释GARCH模型参数的共同决定因素文献。关于究竟有多少个共同因素影响中国股票波动率，现有文献并没有给出明确的答案。

本文拟基于混合分布模型分析影响所有中国股票波动率的因素个数，并分析可能的影响因素。已有的混合模型将个别股票的时间序列作为混合模型的样本。本文首先对所有股票的时间序列(高维数据)分别建立GARCH模型，将建模得到的每个股票的GARCH模型参数作为该股票波动性的代理(低维)数据。将所有股票的低维数据(GARCH模型参数)作为本文混合模型的样本，对每个股票波动代理低维数据进行聚类分析，并分析决定每个股票类别的影响因素。对所有股票的分类可以作为资产配置的依据之一。

2 混合模型与股票波动分析

称一个d-维随机向量Y服从多元正态混合分布。有限正态混合分布(Finite mixture of normal distribution)或有限正态混合混合模型(Finite mixture of normal model))，指的是它的分布密度f(y)有如下形式：

f(y)=p1φ(y;μ1,Σ1)+p2φ(y;μ2,Σ2)+…+pKφ(y;μK,ΣK)

(1)

其中，φ(y;μ,Σ)表示均值向量为μ协方差阵为Σ的多元正态密度函数；K指的是子总体的个数(或成分数)；p1、p2、…、pK分别表示K个子总体的比例，满足条件p1,p2,…,pK>0，且p1+p2+…+pK=1。

混合分布与隐藏变量(latent variable)紧密相关。假设存在一个隐藏变量C，C服从多项分布P(C=k)=pk,k=1,2,…K，而给定C=k条件下Y的分布为：

f(y|C=k)=φ(y;μk,Σk)

这样，Y的边际分布即有(1)的形式。因此，混合分布常用于基于模型的聚类分析(Model-based clustering)。

一个股票市场可能包含数千只股票，每个股票可以用GARCH模型去拟合其波动性。GARCH效应产生的原因是日内信息流到达的数量序列相关[7]。影响所有股票波动率的共同因素(共同随机信息)对不同个股股价波动性的影响不一定相同，而个别股票的波动特征可以用GARCH模型的参数刻画。因此，个股的GARCH模型的参数或呈现不同的类型，即拟合股票的GRACH模型参数或可以被视为服从某种混合分布(若干个子总体混合得到的分布)。

更具体地，影响所有股票价格变化的共同信息，是影响所有股票GARCH效应的共同因素。而同样的宏观经济信息，对不同行业、不同所有制类型的影响不同。用GARCH模型描述股票收益率波动时，模型参数完全决定股票收益率波动特征。我们提出如下假设：

①GARCH模型参数属于有限个分布类：共同因素决定了GARCH模型参数来自混合分布

②公司所有权结构、公司所属行业与GARCH模型参数的分类相关。

经验研究表明，GARCH(1,1)模型能很好地描述股票价格变化的聚集性，可以用GARCH(1,1)模型的参数来刻画所有股票的价格波动特性:

rt=μ+εt

(2)

其中，rt是股票在t日的收益率，μ是rt的均值，ht是给定t-1时刻信息下收益率rt的条件方差，ηt是独立同分布，均值为零、方差为1。(a0,a1,λ1)是对应于该股票的GARCH(1,1)模型参数，a0是股票条件方差的常数项，a1表示前期误差项(信息)对当前条件方差的敏感性，a1越大，则前期的信息对当前条件方差的影响越大，市场信息转换为未来波动性冲击的传播速度越快；λ1是前期条件方差对当前条件方差的敏感性，λ1越大，则前期条件方差对当前条件方差的影响越大，波动性干扰的影响越持久；a1+λ1反映新信息对股票波动影响的持久性，a1+λ1越接近1，则条件方差回复到无条件方差的时间越久。

GARCH(1,1)模型的无条件方差σ2和波动半衰期T的计算公式为：

(3)

波动半衰期T表示条件方差减少一半所需要的时间。

在下面的分析中，将所有股票的GARCH(1,1)模型参数(μ,a0,a1,λ1)的估计值视为样本，用混合分布进行聚类分析，判断股票波动率是否来自有限混合分布总体。如果推断GARCH模型参数估计样本来自混合分布的不同总体，则分别应用列联表(交互分类表)和Multilogisitic(多元logisitic)模型分析公司所有权结构、公司所属行业是否是GARCH模型参数的解释因素。

列联表分析的目的是判明公司的特性(用变量描述)与公司子总体划分之间有无关联，即考察公司特性与子总体划分是否独立。检验的原假设是公司特性与公司的子总体划分独立，检验统计量是皮尔森的拟合优度检验或似然比检验，当原假设成立时，统计量的渐近分布是χ2分布。

应用Multilogisitic(多元logisitic)模型分析公司所有权结构、公司所属行业是否是GARCH模型参数的解释因素，即假设公司的分组概率的对数服从如下模型：

(4)

其中，pi、p0分别为是公司分组为i、0的概率，xj表示所有权性质、所属行业等变量，K表示分组个数。

公式可以变形为：

(5)

式(5)表示各派参数分别属于不同组的概率。

3 数据及基本分析

本文采用2006年—2014年A股上市公司每日股票收盘价数据，从2006年到2014年，中国经济经历了高速增长、面临全球经济危机的冲击、逐步过渡到平稳增长，虽然仅仅9年时间样本，却能够反映中国经济增长的各种特征。本文在样本中剔除了在2006年是ST公司、PT公司、数据缺失和销售收入为0的公司。因为金融业是受到高度监管的公司，所以也将金融、保险业的公司剔除。剔除这些股票之后，获得的总样本个数为1165。本文的数据来自CSMAR数据库和Wind数据库。

本文根据不同性质的股权构成的比例关系，对公司的所有权形式进行划分，用虚拟变量来代表不同所有权类型的企业。本文采用中国证监会的行业分类标准进行行业分类，剔除金融、保险业，分析采掘业、传播与文化产业、电力煤气及水的生产和供应业、房地产业、建筑业、交通运输仓储业、农林牧渔业、批发和零售贸易、社会服务业、信息技术业、制造业和综合类。用虚拟变量代表不同行业。本文将用到每个变量与虚拟变量赋予名称，将变量名称、代码简单定义列于表1和表2。

首先对样本分组做简单的基本统计，统计数据见表3。从表3可以看出，数据中总的样本公司数1165家，六类所有权结构形式的公司数量都有数百家公司。不过，按照行业进行公司分组时，国有控制的企业的发展主要集中在采掘业、电力煤气及水的生产和供应业和交通运输仓储业，而非国有控制的企业的发展主要集中在制造业、信息技术业和农林牧渔业。这可能导致按照行业和所有权结构分组时，有些组包含的样本个数比较少，这是在解释统计数据时必须注意的事实。

表1 行业虚拟变量

表2 所有权比例虚拟变量

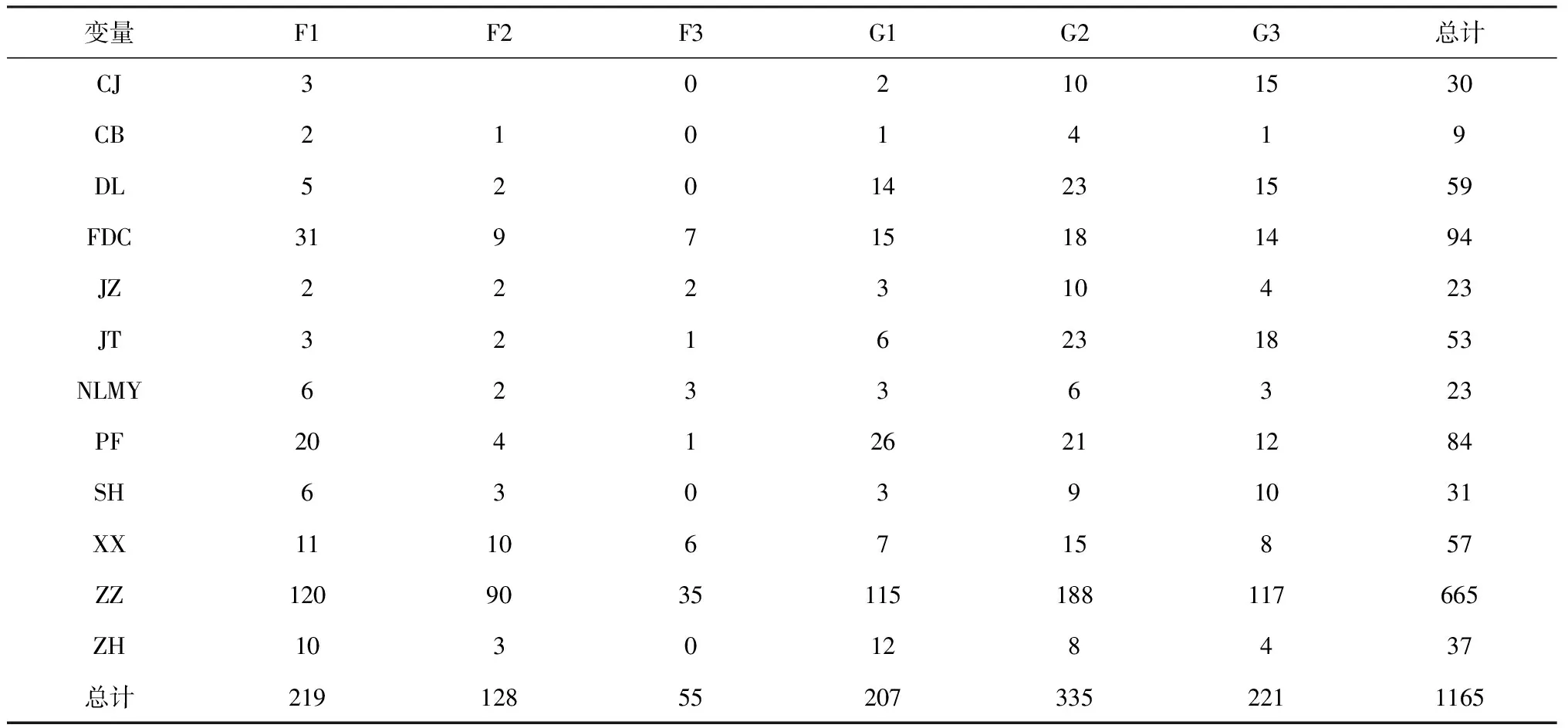
表3 样本分布统计

用GARCH(1,1)模型分别拟合1165只股票收益率，假设(2)式中μ=0拟合模型，根据文献的研究和我们的经验，这样选择的模型几乎能够很好的拟合所有股票收益率(选择μ≠0进行分析得到的结论相同，为节省篇幅计，本文舍弃了对μ≠0时的分析)。对所有1165只股票分别拟合GARCH(1,1)模型，得到每个股票的GARCH模型参数a0,a1,λ1的估计值。将这些参数向量(a0,a1,λ1)的估计值视为3维随机向量的样本，分析这些三维随机向量样本(参数估计)是否服从3元正态混合分布，并分析行业、不同所有制类型是否与参与决定个股书哪个子总体。

4 混合模型拟合分析

⑴混合分布的参数估计

进行统计分析使用的分析软件为免费统计软件R以及R软件包mclust[24-25]。混合模型的参数估计为最大似然估计(MLE)，一般通过应用EM算法[28]得到。特别地，对1165只个股的GARCH(1,1)模型参数用不同成分个数的3元正态混合分布进行拟合，然后比较不同模型(不同成分个数)的BIC统计量[29]。BIC越大表示模型越优，最大BIC对应的模型最好地兼顾了拟合优度以及模型复杂度。

图1描述不同子总体个数多元正态混合模型拟合1165只个股的GARCH(1,1)模型参数的BIC统计量，横轴是子总体个数，纵轴上对应的BIC统计量数值。图1是不同子总体数下的混合分布估计的BIC统计量。需要指出的是，在给定子总体数后，可以考虑对各子分布(多元正正态分布)的协方差阵加上适当的约束：如要求各协方差阵都是相同的(EII)，或要求各协方差阵仅特征根可以不同(VII)，或各协方差阵可以自由变化，无任何约束(VVV)。在分析中考虑了10种不同的协方差阵约束的情形(见图1)，这些情形的具体描述请参见该文献[13]第8页的表1。

图1 BIC检验统计量

根据图1，7个成分协方差无约束(VVV)的混合模型对应的BIC最大。注意到当成分数大于4后，BIC的变化其实很小。本着简约的原则(在检验统计量相同或相似的条件下，选择参数最小的模型)，选择4个成分协方差无约束(VVV)的混合模型为最终模型。

因此，这1165支股票的波动特性具有异质性(成分数大于1)，这些股票的参数向量样本的分布可以看作是4个多元正态分布的混合，而不是来自一个正态分布。

在设定这些股票的参数向量样本来自一个4成分混合多元正态分布的前提下，对参数向量样本进行混合分布分析，可以得到每个个股的GARCH(1,1)模型参数向量属于4个子分布的后验概率。根据每支股票属于各子分布的后验概率，把样本中的股票分成4类(根据最大后验概率原则)，属于同一类的股票的可以认为是同质的。其中子总体1包含35只股票，子总体2包含551只股票，子总体3包含240只股票，子总体4包含339只股票。总股票(样本)数为1165。表4-1是对四个子总体按行业分类统计，表4-2是对四个子总体按所有权性质分类统计。

表4-1 子总体按行业分类——行业相关性

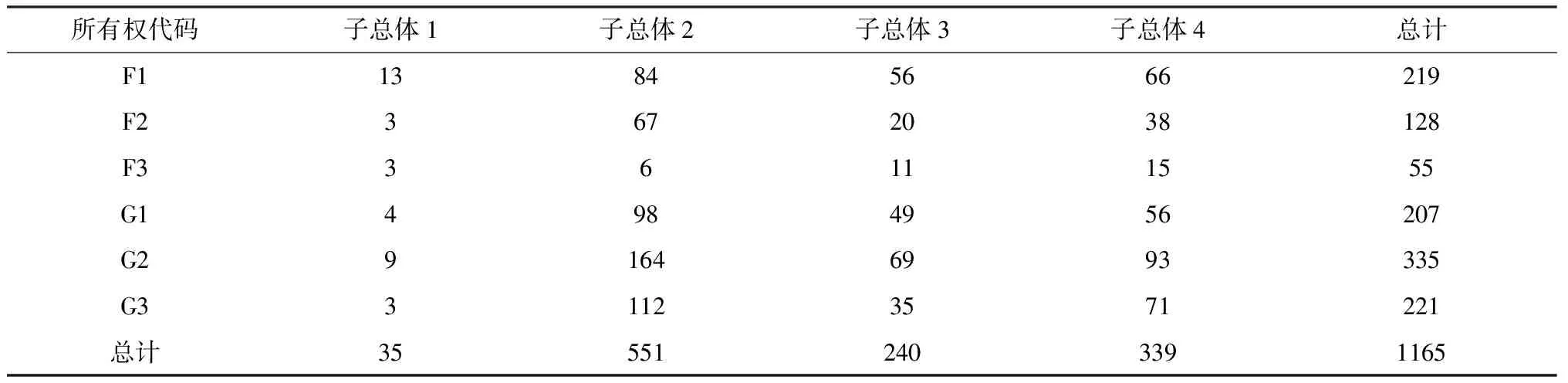
表4-2 子总体按所有权性质分类

选定子总体个数为4后，进一步分析这四个子总体的基本统计。对每个子总体，分别计算这4个子总体的比例、每个子总体中参数向量(a0,a1,λ1)的估计值的均值、协方差阵和相关系数矩阵，分别将计算结果列于表5-1、5-2中。

表5-1

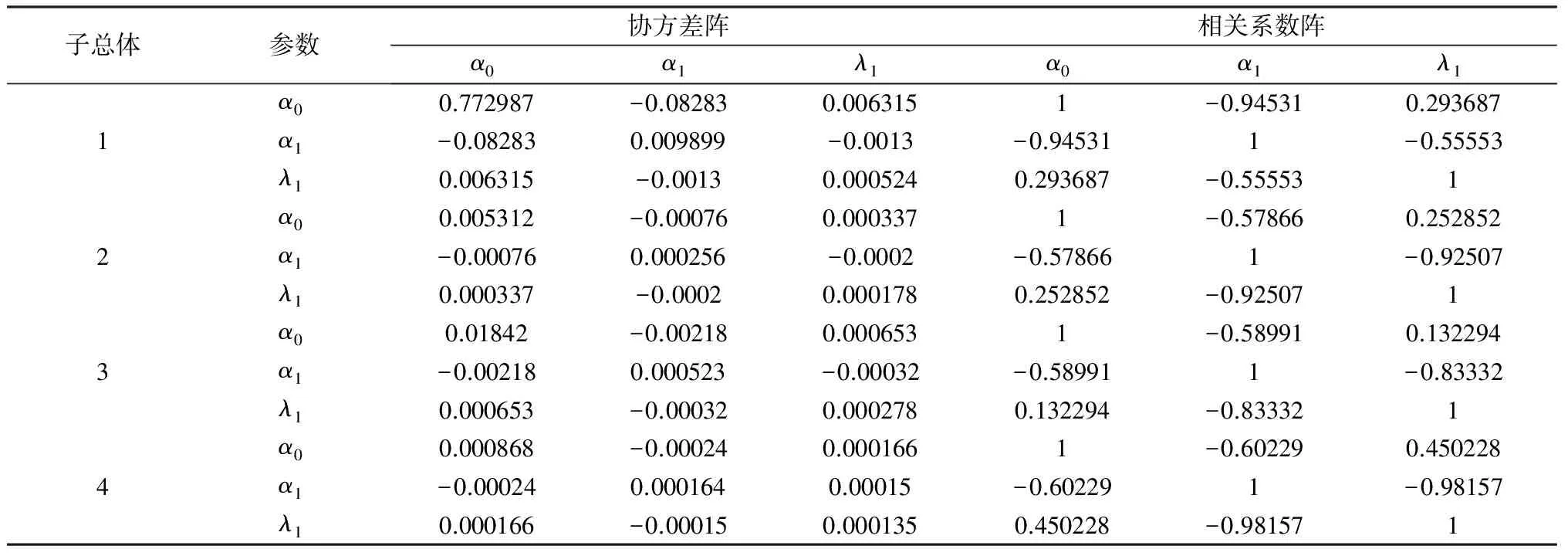
表5-2

根据GARCH(1,1)模型的无条件方差计算公式(3)，分别计算四个子总体对应GARCH模型的无条件方差，列于表5-1。在表5-1中，a1+λ1是将α1均值估计值、λ1均值估计值相加得到，反映股票波动持久性(Persistency)。将表5-1、表5-2中四个总体的参数均值、标准差摘录列入表6。

表6 子总体分布函数的均值与标准差

⑵混合分布的分析

比较表4-1、4-2可以发现，4个子总体股票在各个行业、各种所有权类型中分布并不均匀：子总体股票分布与行业、所有权性质是有关联的。

比较表5-1可以发现，在这四个子总体中，子总体1与其他三个子总体有显著差异。第一个子总体股票个数所占的比例最小，仅仅占3.13%(在1165只股票总样本中仅仅35只股票)，其他3个子总体股票个数虽然也有差异，但在一个数量级上，与子总体1股票所占的比例比较差异不大；子总体1中的股票条件方差的不变项比较大，前期误差项(信息)对当前条件方差的敏感性比较小，前期条件方差对当前条件方差的敏感性比较大，新信息对股票波动影响的持久性较短，股票价格受到新信息冲击之后能够比较快的恢复，子总体1里的股票的波动风险比其他子总体的股票的波动风险大性，而其它子总体里的股票的波动风险差别不大。

注意到表5-2中子总体2、子总体3和子总体4的参数向量的相关系数矩阵很相似，与子总体1的相关系数矩阵差异比较大，说明子总体2、子总体3和子总体4的相关性相似，而他们的差异主要体现在各参数的均值与方差上。子总体1与其他三个子总体各参数的均值、相关性与方差均存在显著差异，是数量级水平不同的差异。而子总体2、子总体3和子总体4的各参数在数量级上是同一水平，但是其大小有差异。

从表6可以看出，子总体1参数对应的标准差最大，约为其它子总体对应值的3倍以上甚至更多，而其他三个子总体参数对应的标准差基本上在一个数量级，说明这三个子总体的GARCH模型参数值的变化范围差不多。这表示子总体1里GARCH模型参数值的变化范围很大，远远大于其他三个子总体的GARCH模型参数，意味着子总体1中不同股票的GARCH模型参数差异较大，而其他三个子总体中股票的GARCH模型参数差别不大，子总体1中的股票波动性的差异比其它子总体里的股票波动性的差异要大。

仔细检查子总体1的35只股票，全部都是出现亏损、重组、增发、资产注入、甚至退市的公司，部分公司甚至公司名称也发生变化。也就是说，子总体1中包含的主要是退市、重组、ST公司、PT公司、重组、增发等类型公司股票。因此，剔除这些公司样本。

综合上述数据分析，我们发现子总体2、子总体3和子总体4的参数向量的相关性相似，而他们的差异主要体现在参数向量的方差和子总体参数向量均值对应的GARCH模型的方差上。子总体1其实包含表现异常的公司股票，其它子总体包含的股票相似度比较高。数据提示：混合分布的分组依据可能是股票GARCH模型参数的均值与方差，而各参数间的相关性相似。

5 股票混合分布的分类归因分析

根据每支股票属于各子分布的后验概率把样本中的股票分成4类，属于同一类的股票的可以认为是同质的。现在分析公司的所有权结构以及公司所属行业是否与股票的分类有关联。现在通过比较子总体2、子总体3、子总体4的GARCH(1,1)模型参数均值向量来描述各子总体的特征，然后检查这些类的公司的所有权结构、所属行业是否有差异。子总体2包含551只股票，子总体3包含240只股票，子总体4包含339只股票。总股票(样本)数为1130，各子总体的行业分布和所有权分布参见表4-1和表4-2。

下面分别用列联表和多元logistic模型分析公司所有权、所属行业差异与公司子总体分组是否有关。首先进行列联表分析，然后进行多元logistic模型分析。

⑴列联表分析

表7是各子总体的行业分布和所有权分布及列联表(交互分类表)检验统计。表7中第一列是变量名称，第二列是变量值，第三、第四和第五列分布是变量取得该值时子总体2、子总体3和子总体4中的股票个数及占比，最后一列是原假设成立时用样本数据计算检验统计量的值对应的概率。

表7中的变量是行业虚拟变量(Dummy variable)和所有权虚拟变量，变量名称的含义见表1和表2。行业虚拟变量等于1，表示属于这个行业，等于0表示不是这个行业；所有权虚拟变量的含义相同。子总体中的股票个数根据变量分别计算，括号中的数值是相应的比例。下面以子总体2中变量G1对应的股票个数(第三列中的第二行、第三行)来说明相关数值的含义。453表示子总体2中对应G1等于0(不属于G1)的股票个数有453个，453后面括号中的48.9表示子总体2中不属于G1的股票个数占子总体1中股票的比例为48.9%；98表示子总体2中G1等于1(属于G1)的股票个数有98个，后面括号中的48.3表示子总体2中属于G1的股票个数占子总体2中股票的比例为48.3%(子总体2中总股票个数是453+98即551个)；第四、第五列下面的数据同样解释。

表7 各子总体的行业分布和所有权分布及列联表检验

注：*和**分别表示在10%和5%的显著性水平上拒绝参数等于零的原假设

表7 的列联表分析的目的是判明公司的特性(用变量描述)与子总体划分之间有无关联，即考察公司特性与子总体划分是否独立。在下面的分析中，分别对每个变量进行2×3列联表分析，检验该变量与子总体划分独立的原假设。

现在以变量G1来解释列联表的统计分析方法。在表7中的第二、第三列构成的2×3列联表中，若以pi(i=2,3,4)分别表示属于股票子总体2、3、4的概率，pj(j=0,1)分别表示股票特性为G1等于0和G1等于1的概率，pij表示股票同时属于子总体i(i=2,3,4)和股票特性G1等于j(j=0,1)的概率，2×3列联表统计分析的原假设为：pij=pi×pj(i=2,3,4;j=0,1)，即公司特性与股票属于是否属于特定子总体无关，股票在三个子总体的比例相同。检验统计量(χ2统计量)为皮尔森的拟合优度检验或似然比检验。当原假设成立时，统计量的渐近分布是自由度为3的χ2分布。表7中的第六列即检验统计量对应的概率值。

以变量G1为例比较表7中的数据。在子总体2包含的551只股票中，有98只(17.8%)为G1，而453只(82.2%)非G1；子总体3里有49只(20.4%)为G1，而191只(79.6%)非G1；子总体4里有56只(16.5%)为G1，而283只(83.5%)非G1。χ2统计量对应的p-值为0.479(47.9%)。因此，不能拒绝“这三个子总体是有相同比例的G1”的原假设。其他数据的解释类似。

特别地，注意到4个子总体有显著不同比例的F1(p-值为0.02)，FDC(p-值为0.044)，SH(p-值为0.015)，ZZ(p-值为0.079)。因此，拒绝这四个子总体是有相同比例的“非国有股权分散公司”、“社会服务业”、“房地产公司”、“制造业公司”原假设。

对照表7可以看到，非国有股权分散公司(F1)在子总体3中比例(23.3%)最高，在子总体2中比例(15.2%)最低；房地产公司(FDC)在子总体4中比例(11.2%)最高，在子总体3中比例(6.2%)最低；社会服务业(SH)在子总体4中比例(4.7%)最高，在子总体3中比例(.2%)最低；制造业公司在子总体3中的比例(62.0%)最高，在子总体4中的比例(52.8%)最低。

观察表5-1注意子总体2的无条件方差(10.69)最大，子总体4的无条件方差次大(10.57)，子总体3的无条件方差最小(10.38)。因此，非国有股权分散公司、制造业公司相对偏向低风险，社会服务业、房地产公司相对偏向高风险公司。出现这种现象的原因有待进一步研究。我们猜测，这是样本期2006-2014内国有绝对控股公司、房地产业、制造业发展的中国经济形式有对应关系。

⑵多元logistic模型分析

在混合分布分析中，发现总体可以分为四个子总体。其中，子总体1主要有少量“噪音”样本组成。因此，下面仅仅分析子总体2、子总体3和子总体4的划分是否与公司的所有权结构、所属行业有关系。可以用多元logistic模型来分析子总体和公司的所有权结构、所属行业的关系，从而找出影响股票波动性分类的因素。用回归分析估计(6)中的多元logistic模型，结果列于表8 中。

(6)

在多元logistic模型统计分析中，公式(6)中k=2，待估模型参数是α1、β11、β12、α2、β21、β22。p0是公司分组属于子总体4的概率，p1、p2分别是公司属于子总体2、子总体3的概率。提醒注意，因为多元logistic分析中剔除了子总体1的样本，这里的p0、p1、p2与混合分布分析时得到的股票属于某子总体的概率不同，是将混合分布是股票属于该子总体的概率除以股票不属于子总体1的概率(即一减去股票属于子总体1的概率)。

表8 多元logistic模型参数估计

**表示在5%的显著性水平上拒绝参数等于零的原假设

我们仅考虑后3个子总体，以子总体4为对照，通过变量选择后，得到如上的最终模型。通过这个模型，制造业的公司(股票)更可能属于子总体2和3子总体，而不是子总体4。表5-1提示子总体4的波动持续性最大，因此，制造业的公司股票波动的持续性相对较低。

6 结语

论文以GARCH模型描述股票的波动特性，应用混合分布以中国上市公司股票波动特性进行分组，研究发现，中国上市公司可以被分为4个子总体，每个子总体股票在各个行业、各种所有权类型中分布并不均匀：子总体股票分布与行业、所有权性质是有关联的。其中，子总体1主要包含表现异常的公司股票，子总体2、子总体3和子总体4的参数向量的相关性相似，而他们的差异主要体现在参数向量的方差和子总体参数向量均值对应的GARCH模型的方差上。

应用列联表法分析发现，非国有股权分散公司、制造业公司相对偏向低风险，社会服务业、房地产公司相对偏向高风险公司。对子总体2、子总体3和子总体4中的股票，以子总体4为对照，对三个子总体进行多元logistic模型统计分析发现，制造业的公司(股票)波动的持续性相对较低。

总之，混合分布是对股票特性进行分组的良好工具，能够清晰地将异常股票寻找出来，并将异常股票分在同一子总体中。

[1] Fama E F. French K R, Dissecting anomalies with a five-factor model[J].Review of Financial Studies, 2016, 29(1): 69-103.

[2] Fama E F. French K R. A five-factor asset pricing model[J].Journal of Financial Economics，2015，116(1)：1-22.

[3] Jegadeesh N,Titman S. Returns to buying winners and selling losers: Implications for stock market efficiency[J].Journal of Finance,1993, 48, 65-91.

[4] Engle R F. Autoregressive conditional heteroskedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica, 1982, 50(4):987-1007.

[5] Bollerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics,1986, 31(3):307-327.

[6] Bollerslev T. A conditionally heteroskedastic time series model for speculative prices and rates of return[J]. Review of Economics and Statistics,1987, 69(3), 542-547.

[7] Lamoureux C G, Lastrapes W D. Heteroskedasticity in stock return data: Volume versus GARCH effects[J]. Journal of Finance, 1990, 41(1): 221-229.

[8] Bessembinder H, Seguin P J. Price volatility, trading volume, and market depth: Evidence from futures markets[J]. Journal of Financial and Quantitative Analysis, 1993, 28(1):21-39.

[9] 赵军力, 梁循. 基于TrTS取样的股票收益率RV测度的改进[J]. 中国管理科学, 2015, 23(7):26-34.

[10] 刘祥东, 范彬, 杨易铭,等. 基于M-Copula-SV-t模型的高维组合风险度量[J]. 中国管理科学, 2017, 25(2):1-9.

[11] Fraley C, Raftery A E. Model-based clustering, discriminant analysis and density estimation[J]. Journal of the American Statistical Association.2002, 97(458):611-631.

[12] Dempster A P, Laird N M, Rubin D B.Maximum-likelihood from Incomplete Data via the EM Algorithm[J]. Journal of the Royal Statistical Society,1997, 39(1): 1-38.

[13] Schlattmann P. Medical applications of finite mixture models[M]. Springer Series: Statistics for Biology and Health,2009.

[14] Thomas E M, Temko A, Lightbody G, et al, Gaussian mixture models for classification of neonatal seizures using EEG[J].Physiological Measurement,2010, 31(7):1047-64.

[15] 刘艳琪，胡亨伍.基于EM 算法的混合模型医学图像分割[J].计算机工程，2012, 38(2):231-233.

[16] Tauchen G E, Pitts M. The price variability-volume relationship on speculative markets[J]. Econometrica, 1983, 51(2):485-505.

[17] Andersen T G. Return volatility and trading volume: An information flow interpretationof stochastic volatility[J]. Journal of Finance,1996, 51(1):169-204.

[18] Lamoureux C G, Lastrapes W D. Endogenous trading volume and momentum in stock-return volatility[J]. Journal of Business & Economic Statistics, 1994, 12(2):253-260.

[19] Liesenfeld R. Dynamic bivariate mixture models: Modeling the behavior of prices and trading volume[J]. Journal of Business & Economic Statistics,1998, 16(1): 101-109.

[20] Mitchell M L, Mulherin J H. The impact of public information on the stock market[J]. Journal of Finance, 1994, 49(3):923-950.

[21] Berry T D, Howe K M. Public information arrival[J]. Journal of Finance,1994, 49(4), 1331-1346.

[22] Liesenfeld R. A generalized bivariate mixture model for stock price volatility and trading volume[J]. Journal of Econometrics,2001, 104(1): 141-178.

[23] 杨瑞成，秦学志，陈田，等，基于混合分布单因子模型的CDO定价问题[J]，数理统计与管理，2009, 28(6)，1082-1090.

[24] Fraley C. Raftery A E. Murphy T B,et al, Mclust Version 4 for R: Normal mixture modeling for model-based clustering, classification, and density estimation technical[R]. Report No. 597,University of Washington.

[25] Thomas E M,Femko A,Lightbody G,et al. Gaussian mixture models for classification of neonatal seizures using EEG[J]. Physiological Measurement, 2010,31(7):1047-1064.