影响矩阵法在大跨径斜拉桥二次调索中的应用
2018-03-08李飞
李 飞
(中交路桥技术有限公司 北京 100011)
斜拉桥在施工过程中由于种种原因,可能导致成桥后索力与目标索力存在偏差,按照当前规范,成桥后索力偏差不应超过±5%,当接近或超过该值时则需要进行索力调整,实现成桥状态的最佳内力分布。
传统的在施工阶段中尝试不同的张拉力方法实际是通过人工反复尝试不同的索拉力组合以达到设计目的的方法,因为实际张拉某根索后,其他索的索力也会随之变化,这种相互影响导致了人工反复尝试的办法效率很低,且很难找到理想的成桥状态。并且传统的尝试方法是逐根调整索力,无法从全局上考虑效应,所以很难直接找到满足所有要求的单根索力,更难以从全局的观点来实现设计思想[1]。
本文采用影响矩阵法对依托工程进行二次调索,有限元计算采用midas Civil软件。
1 影响矩阵法原理
影响矩阵法已经广泛应用于斜拉桥调索过程中,影响矩阵主要涉及概念为受调向量、施调向量及影响矩阵。其中,受调向量指结构物中关心截面上m个独立元素组成的列向量。它在调值过程中接受调整,以期达到某种期望状态,受调向量记为:
D=(d1,d2,…,dm)T
施调向量。指结构中指定可以实施调整以改变受调向量的n个独立元素(n≤m)所组成的列向量,记为
X=(x1,x2,…,xn)T
本文中索力调整值即为施调元素。
影响向量。指施调向量中第j个元素xj发生单位变化,引起受调向量D的变化量,记为
Aj=(a1j,a2j,…,amj)T
影响矩阵。指n个施调向量分别发生单位变化,引起n个影响向量依次排列组成的矩阵,记为
理论上,只要将单位施调向量逐一加到结构上,分别求出相应的影响向量,就能形成结构的影响矩阵。
当结构满足线性叠加时,有
AX=D
(1)
式(1)可唯一求得施调向量X。向量X表示要使关心截面力学量达到D,必须使施调向量产生X的相应变化[2]。
2 调索拔出量控制
如果调索是一次完成的,则可将由影响矩阵计算出的索力调整向量X直接施加于结构,完成索力调整,但实际调索是逐根进行的,因此,该方法不可行。解决的办法有2个:①将影响矩阵与调索顺序结合,确定一个最优调索过程;②考虑到张拉端拉索拔出量与施工过程无关,将索力调整值换算为张拉拔出量,则可避免张拉顺序对调索的影响。前者可通过约束函数利用最小二乘法等方法确定,计算量稍大;后者则只需在确定索力调整变化量的基础上,求出索力调整前后的无应力长度改变量,即在索力调整时只需控制拉索拔出量即可,张拉控制与施工顺序无关,且在白天夜间都可以进行,将大幅提高施工效率。
拔出量计算可按式(2)计算。
ΔL=ΔLe+ΔLf+ΔLl+ΔLt
(2)
式中:ΔLe为在拉索在调整力X作用下的弹性伸长量;ΔLf为拉索调整前后垂度变化引起的伸长量;ΔLl为拉索调整前后主梁竖向变位引起的伸长量;ΔLt为拉索调整前后主塔水平变位引起的伸长量[3]。
一般来说,如果成桥后索力调整值较小,且调索过程中拉索都处在高应力状态,则ΔLf非常小,计算时可忽略不计。主梁合龙后整体刚度较悬臂阶段大很多,一般情况下ΔLl及ΔLt也较小。由此可见,成桥后索力调整,若调整量较小,则影响拔出量的主要因素为弹性伸长量ΔLe。
3 工程实例
泉州湾跨海大桥主桥为跨径800 m的3塔分幅组合梁斜拉桥,跨径布置为70 m+130 m+400 m+130 m+70 m,见图1。主梁采用PK式流线形扁平组合梁,斜拉索采用镀锌平行钢丝。

图1 泉州湾跨海大桥主桥总体布置图(单位:cm)
3.1 成桥索力调整量计算
成桥后实测索力与理论索力的见表1(限于篇幅仅列出部分数据)。
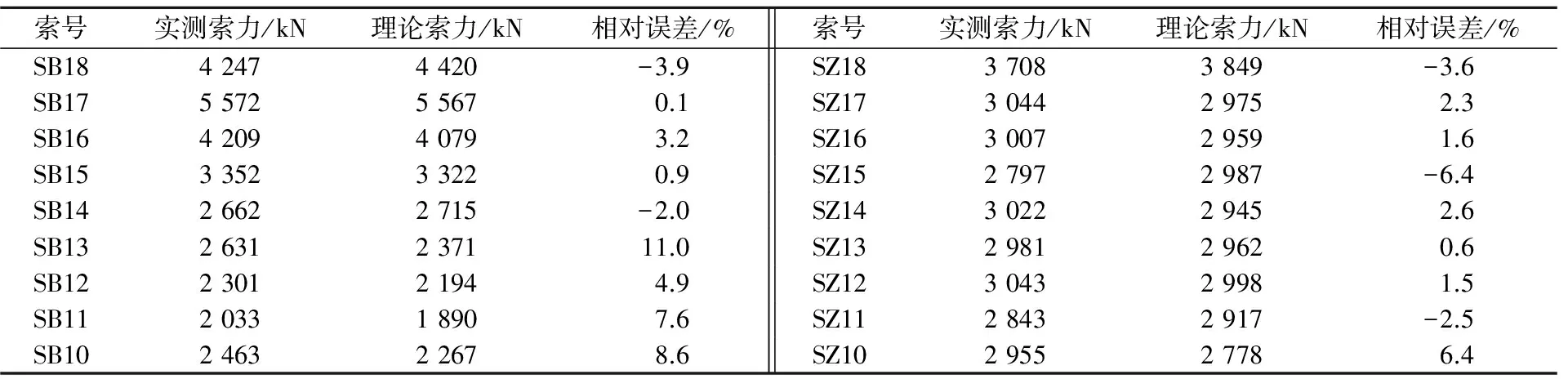
表1 成桥索力偏差
注:SB18代表边跨18号索,SZ18代表中跨18号索。
首先求索力影响矩阵A。如对拉索SB1,当给其施加一个单位力x1=1时,其余所有拉索相应的索力变量记为A1={a11,a21,…,ai1}T。同理,如果给j号拉索施加单位力xj=1,相应的其余所有拉索索力变量记为Aj={a1j,a2j,…,aij}T,i为全桥拉索总数。由此可以得出索力影响矩阵。
限于篇幅,列出SB13~SB18影响矩阵如下。

一般来说,斜拉桥成桥后索力调整值远小于其调整前索力值,故可忽略索力调整引起的索的拉伸刚度变化,并用线形叠加的方法由影响矩阵求出索力的调整值。
AX=ΔT
式中:A为索力影响矩阵;X为索力调整向量;ΔT为索力偏差向量(由实测索力与理论索力差值求得)。
由上式容易求得索力调整向量X,即所要调索的数值,见表2。
表2“理论调整”列为理论计算调整值,考虑到部分索力偏差较小,并未超过规范要求值,调整意义不大,所以认为无须按照理论计算进行全部拉索索力调索,应该在保证调索后所有索力满足规范要求的基础上,尽量减少调索数量。通过优化,最终调索数量由36根减少为14根,调整情况见表2中“实际调整”列。
3.2 锚杯拔出量计算
考虑到千斤顶的精度问题,将每根索索力调整对应的拔出量作为实际调索的主要控制参数,减小了千斤顶精度不足引起的误差,同时由于拔出量非常小,温度对其影响可忽略不计,排除了调索对张拉顺序及环境温度的要求,避免了以往调索多需要选在夜间温度相对稳定的时候进行,提高了调索效率,拔出量计算见表3。有了拔出量则可根据现场施工条件灵活确定调索时间。
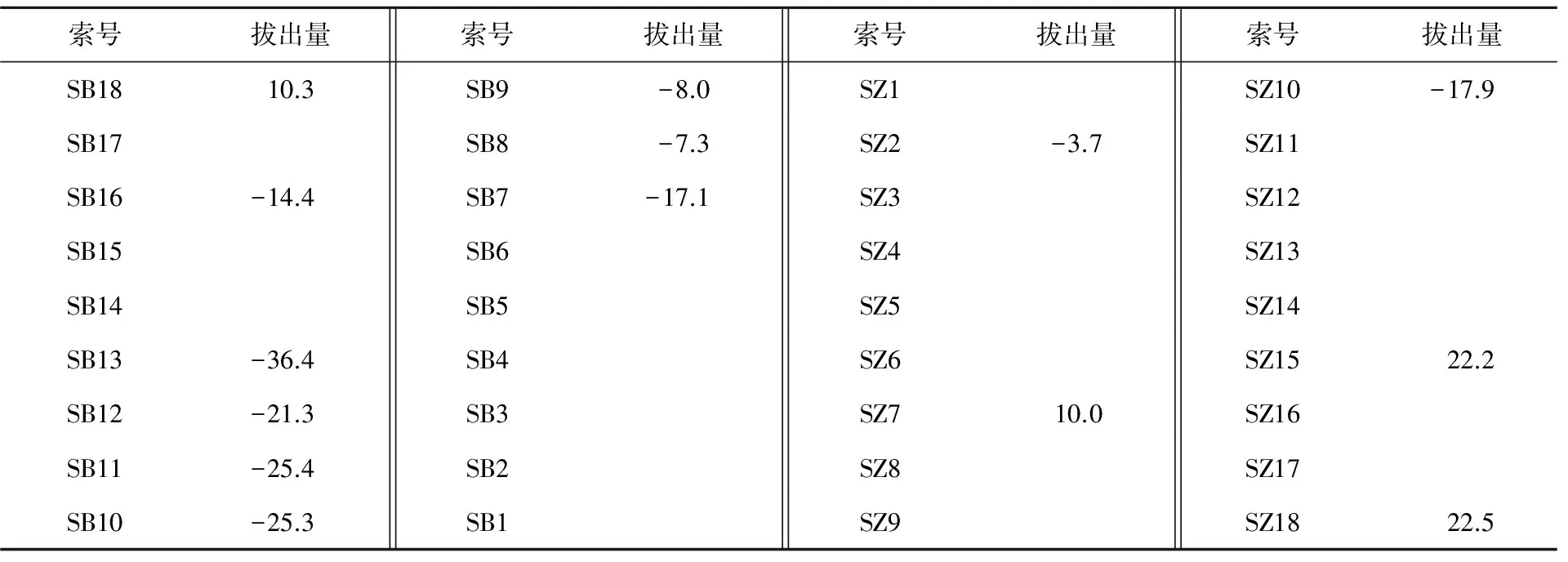
表3 锚杯拔出量 mm
3.3 线形及应力情况
调索前后主梁最大位移变化值为-12.6 mm,发生在SZ10号索附近截面,主塔向中跨侧偏移7 mm;调索引起的桥面板最大拉应力增量为0.24 MPa(成桥后桥面板压应力储备在2~6 MPa之间),最大压应力增量为0.19 MPa,钢梁的拉压应力增量均未超过3 MPa。由此可见,由于调索数量及调整值均较小,且调索的工况是在主桥合龙后,此时结构整体刚度大,所以调索对于结构的线形和应力影响均较小。
3.4 最终成桥索力
经过索力调整后,最终成桥索力偏差及调索前索力偏差见图2。
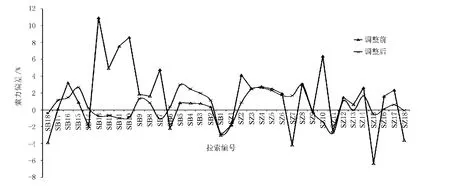
图2 成桥索力偏差
由图2可见,经过调索后,整体索力较调索前有明显改善,最大偏差控制在4%以内,满足规范要求。
4 结论
1) 利用影响矩阵法进行大跨径斜拉桥成桥后索力调整,概念清晰,方法简便。
2) 实际调索是逐根进行的,为避免张拉顺序带来的计算工作,可利用拔出量作为调索的主控参数。
3) 利用上述方法进行索力调整可大幅提高工作效率,实现索力优化的同时对结构线形和应力影响很小。
[1] 江安.应用影响矩阵进行无背索斜拉桥调索[J].交通科技,2010(7):61-64.
[2] 伏首圣.公和斜拉桥索力的确定与调整[D].大连:大连理工大学,2003.
[3] 王美.红枫大桥成桥后索力调整及调索顺序的优化[D].大连:大连理工大学,2005.
[4] 蒋伟冬,张谢东,秦川,等.斜拉桥换索过程中旧索旋转问题研究[J].武汉理工大学学报(交通科学与工程版),2017,41(2):333-337.
