基于动荷系数的路面行驶质量水平评价

杨 壮 田 洋

(长江勘测规划设计研究有限责任公司 武汉 430010)

路面平整度是路面行驶质量评价的一个重要指标，可有效反映路面行驶的经济性、舒适性和安全性。美国材料试验协会(ASTM)将路面平整度定义为道路表面相对于理想平面的竖向偏差值，这种偏差会影响到车辆的动力特性、行驶质量、路面所受动荷载和排水性能[1]。1986年，Sayers在巴西等国家进行了路面平整度试验，并提出了国际平整度指数(international roughness index，IRI)，即1/4车辆模型以80 km/h速度在路面上行驶时悬挂系统的单位距离纵向累计位移量[2]。

目前IRI是国际公路领域应用最广泛的平整度指标，我国JTG H20-2007 《公路技术状况评定标准》通过直接建立路面行驶质量指数(riding quality index，RQI)与IRI的换算关系，提出了路面行驶质量水平评价方法[3]。该评价方法主要考虑了路面不平整度的影响，忽略了车辆实际运行速度与设计速度的差异影响。通过车-路耦合动力学模型可知，车辆运行速度是影响车辆动荷系数的重要因素之一，而动荷系数的变化对IRI存在一定影响。因此，考虑路面平整度与车辆实际运行速度的综合影响，提出基于动荷系数的路面行驶质量水平评价方法，具有十分重要的意义。

1 路面平整度模型

对于路面不平整导致的车辆振动，Sun Lu[4]等人提出了IRI与路面功率谱密度的具体关系式

(1)

式中：Ω为空间频率，是路表面空间波长λ的倒数；ω为时间角频率；v为车辆行驶速度；Gξ(Ω)路面空间功率谱密度；Hs(ω)为1/4车辆模型弹簧质量的频率响应函数，在IRI的定义中，c=6.0 s-1，μ=0.15，k1=653 s-2，k2=63.3 s-2。

根据GB T7031-2005 《机械振动道路路面谱测量数据报告》，路面功率谱密度可用空间频率表示为

Gξ(Ω)=Gξ(Ω0)(Ω/Ω0)-ω

(2)

式中：Ω0为空间参考频率，Ω0=0.1 m-1；Gξ(Ω0)为参考空间频率Ω0下的路面空间功率谱密度值，称为路面平整度系数；ω为频率指数，是双对数坐标上斜线的斜率，它决定路面功率谱密度的频率结构，其表达式为

ω=2πf=2πt-1=2π(v/l)=2πvΩ

(3)

将式(2)、(3)代入(1)中得：

(4)

根据国际道路会议常设委员会(PIARC)[5]提出的路面构造分类，路面平整度的波长范围为(0.5,50 m)，对应的空间频率范围为(0.02,2 m-1)。对式(4)进行积分计算时，取空间频率Ω范围为(0.02, 2 m-1)，其计算结果为

(5)

2 车辆垂向振动模型

车辆系统是一个复杂的多自由度“质量-刚度-阻尼”动力学系统。根据实际问题需要，本文采用简化的双自由度1/4车辆模型作为垂向振动分析模型[6]，见图1。

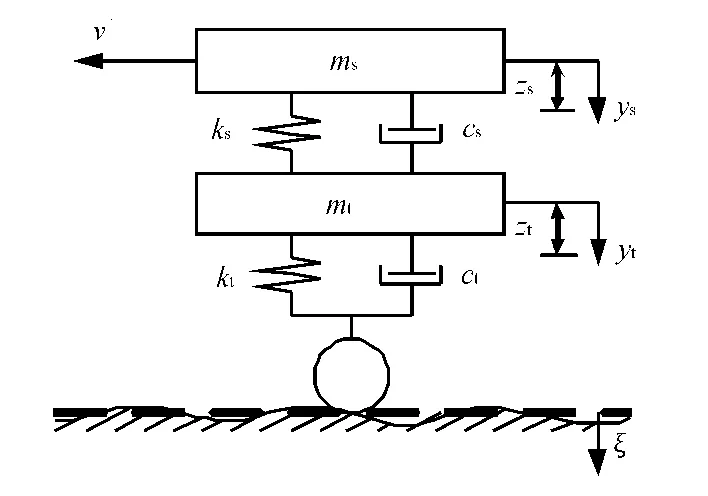
v-车辆行驶速度；ms-簧载质量；mt-非簧载质量；ks-悬挂系刚度系数；kt-轮胎刚度系数；cs-悬挂系缓冲阻尼系数；ct-轮胎阻尼常数；zs，zt-簧载质量和非簧载质量的垂直相对位移；ys，yt-簧载质量和非簧载质量的垂直绝对位移；ξ为纵断面高程(路面不平整度)。

图1 1/4车辆模型

根据文献[4]，重载车辆是引起路面损坏的主要原因，本文对车辆模型各参数取值分别为ms=4 450 kg，mt=550 kg，ks=1 150 kN/m，kt=1 800 kN/m，cs=15 kN·s/m，ct=2 kN·s/m。

把车辆模型视为多刚度体系，根据D’ Alembert原理，系统中每个刚体在任意瞬态均处于动力平衡状态，则可得到车辆振动模型的动力平衡方程为

(6)

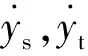
根据车辆模型的垂向位移关系有

(7)

将式(7)代入(6)中作变量代换，根据线性系统理论，对方程组两边同时关于时间进行傅里叶变换，可得到该振动系统的频率响应函数：

(8)

式中：Hs(ω)与Ht(ω)分别为簧载质量与非簧载质量的频率响应函数；Dt(ω)，Ds(ω)和D(ω)的表达式为

(9)

其中：h=ms/mt;αs=cs/ms；αt=ct/mt；βs=ks/ms；βt=kt/mt。

根据随机过程理论，路面平整度可以模型化为零均值的高斯遍历过程，而式(6)控制的振动系统为线性时不变系统，则响应功率谱密度与激励功率谱密度存在以下关系。

(10)

式中：Szs(ω)与Szt(ω)分别为簧载质量与非簧载质量的相对位移响应；Sξ(ω)为时间角频率表示的路面平整度功率谱密度。

3 动荷系数计算

通过图1的车辆振动模型，可将车辆作用于路面的动荷载表示为

(11)

式中：t为作用时间；动荷载Pd(t)为具有零均值的平稳正态过程。

根据文献[7]可知，由路面不平整产生随机荷载的功率谱密度Sp(ω)可表示为

(12)

P.F.Sweatman[8]认为作用于路面的车辆动荷载服从于均值为零，标准差为σp的正态分布。将式(12)代入(2)中，计算得到以空间频率表示的单边功率谱密度Gp(f)和标准差σp分别为

(13)

本文取可靠度为99%时可能出现的最大附加荷载值作为车辆动荷载。

Pd=Ps+3σp=(ms+mt)g+3σp

(14)

结合式(13)和式(14)，得到动荷系数Kd的计算公式为

(15)

根据黄立葵等[9]的研究，在积分计算时空频率范围通常取(0.02, 2 m-1)，在常用车速30～120 km/h的条件下，换算成时间频率范围(0.67, 16.7 Hz)，该范围能将簧载质量固有频率1～4 Hz和非簧载质量固有频率10～15 Hz有效地覆盖在内。对式(15)进行积分计算(ω=2，Ω0=0.1 m-1)得

(16)

式中：c0为系数，c0=10-3m0.5s0.5；其他符号采用SI单位。

根据IRI与路面功率谱密度的关系，将式(5)代入(16)中，有

(17)

4 路面行驶质量水平评价

根据JTG H20-2007 《公路技术状况评定标准》，目前我国通常采用路面行驶质量指数RQI对路面行驶质量水平进行评价，RQI可通过式(18)计算得到，其评定标准见表1。

(18)

式中：a0为评价系数，高速、一级公路采用0.026，其他等级公路采用0.018 5；a1为评价系数，高速、一级公路采用0.65，其他等级公路采用0.58。

表1 路面行驶质量评定标准(RQI)

将式(18)代入(17)，则可建立动荷系数Kd的与RQI的关系式。

(19)

式中：vd为车辆设计速度，与公路等级、地形和地质条件相关，现行规范JTG B01-2014 《公路工程技术标准》中对不同等级公路的车辆设计速度做出了明确规定。

根据式(19)，取不同等级公路下的设计速度值代入进行计算，可得到基于动荷系数的路面行驶质量水平评价诺谟图，见图2。

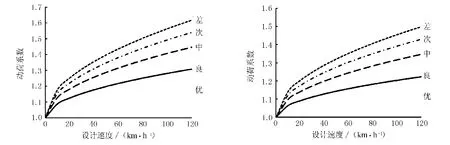
a) 高速、一级公路 b) 其他等级公路

图2 路面行驶质量水平评价诺谟图

由图2可见，不同等级公路在不同设计速度下的动荷系数评定标准差异较大；当公路等级与设计速度一定时，行驶车辆的动荷系数越小，路面行驶质量水平越高。

5 结语

1) 根据国际平整度指数IRI与路面功率谱密度的关系，基于1/4车辆模型，得到99%可靠度下动荷系数与国际平整度指数IRI及车辆运行速度的关系式，由其可知，动荷系数随着IRI和车速的增大而逐渐增大。

2) 基于现有路面行驶质量指数RQI的评定标准，考虑路面平整度和车辆运行速度的综合影响，分别提出了不同等级公路基于动荷系数的路面行驶质量水平评价诺谟图。

[1] Terminology Relating to Traveled Surface Characteristics Annual Book of ASTM Standards: ASTM E867-97[S].West Conshohocken:American Society for Testing and Material,1999.

[2] SAYERS M W, GILLESPIE T D, QUEIROZ C A V. The international road rough-ness experiment:establishing correlation and calibration standard for measurements[R]. World Bank Technical Paper,1986.

[3] 公路技术状况评定标准:JTG H20-2007[S].北京:人民交通出版社,2007.

[4] SUN L, ZHANG Z M, RUTH J, et al. Modeling indirect statistics of surface roughness[J]. Journal of Transportation Engineering,2001,127(2):105-111.

[5] PIARC.Technical committee report on surface characteristics[C].18th World Road Congress, Brussels,1987.

[6] SUN L, DENG X J. Predicting vertical dynamic loads caused by vehicle pavement interaction[J]. Journal of Transportation Engineering,1998,124(5):470-478.

[7] 邓学钧.车辆-地面结构系统动力学研究[J].东南大学学报,2002,32(3):474-479.

[8] SWEATMAN P F. A study of heavy vehicle swept path performance[J].Special Report Australian Road Research Board,1991,48:35-41.

[9] 黄立葵,盛灿花.车辆动荷系数与路面平整度的关系[J].公路交通科技,2006,23(3):27-30.