牵引车动力总成悬置系统优化分析*
2018-03-07郑利锋王铁张瑞亮
郑利锋 王铁 张瑞亮
(太原理工大学,太原 030024)
1 前言
车辆舒适性主要受振动影响,引起车辆振动的主要振源有发动机工作振动激励、路面随机激励及发动机以外旋转部件的不平衡激励。其中发动机作为激励源对整车NVH性能和舒适性有较大影响。
本文针对某牵引车使用铝壳代替铸铁壳变速器,动力总成升级后出现怠速工况振动较大问题,通过AD⁃AMS软件对悬置系统刚体模态进行仿真分析,并结合模态测试分析验证仿真模型的有效性。以悬置刚度为优化参数,悬置系统主振动能量分布的加权组合为优化目标,给出优化后悬置刚度参数。最后,在怠速工况下对转向盘振动量和悬置传递率进行测试,分析并评价悬置系统优化后对整车振动性能的改善效果。
2 动力总成悬置系统分析
考虑到本文研究的牵引车动力总成通过四点平直橡胶悬置安装到车架上,为了建立相应的理论分析模型,做了以下简化假定:
a.动力总成相对平衡位置的位移较小,可认为动力总成的随动坐标与整体坐标重合;
b.由于动力总成的刚度远大于悬置刚度,动力总成简化成刚体;
c.橡胶悬置在局部坐标下,考虑3个方向的平动刚度和阻尼,忽略旋转刚度和阻尼;
d.动力总成惯性矩和惯性积不随时间变化;
e.车架及底盘被看作刚体支撑。
2.1 建立动力总成运动方程
牵引车动力总成系统模型由发动机、离合器、变速器及附件组成,通过4个平置橡胶悬置连接到车架上,布置示意图如图1所示。坐标系Goxyz固定到动力总成的质心上并处于系统静平衡位置。x轴平行于车辆前进方向,z轴垂直向上,y轴垂直于xy平面向左。橡胶悬置按照图1所示进行布置。其中,1-4代表悬置布置位置。
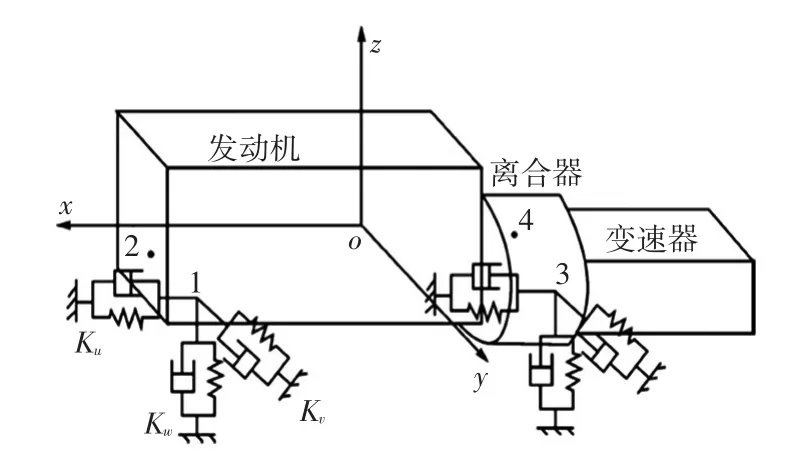
图1 动力总成悬置系统6自由度模型示意图
基于假设和Lagrange原理,得到动力总成6自由度运动方程如下:
2.2 系统评价要求
动力总成悬置系统设计的优劣主要通过系统频率是否匹配合理来进行评价。图2为不同阻尼下放大系数随频率变化的曲线。悬置频率匹配的目的是降低发动机振动向车架的传递,同时减少来自路面激励向发动机的传递。为了获得较好的发动机隔振效果,动力总成悬置系统的各阶固有频率一般不应高于发动机激励频率的倍。对本文研究的牵引车搭载六缸四冲程发动机,怠速转速为600 r/min,发动机点火频率为30 Hz,因此悬置系统的频率不应高于21.2 Hz。为避开路面激励的低频振动,悬置系统固有频率应大于路面激励频率的4/3倍。由于路面激励频率通常不超过3 Hz,因此要使悬置系统的固有频率大于3 Hz/0.75(即4 Hz)。考虑到悬架和车身的固有频率也在低频范围,接近5 Hz,因此,悬置系统的各阶固有频率一般设计在5~21.2 Hz之间。
3 动力总成悬置系统模态仿真分析
应用ADAMS软件对动力总成悬置系统刚体模态进行仿真计算,并结合采用序列二次规划法SQP(Sequen⁃tial Quadratic Programming)算法进行优化分析。
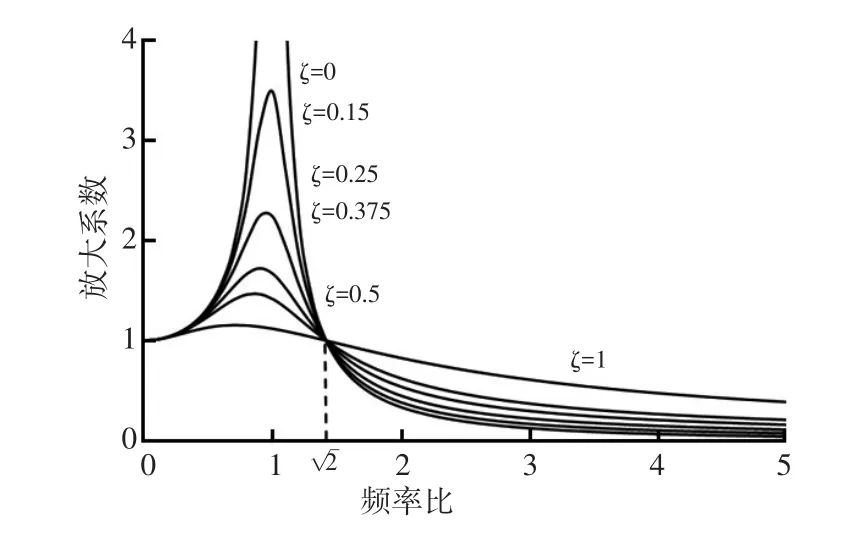
图2 传递率随频率比变化曲线
3.1 建立动力总成6自由度计算模型
假定动力总成为刚体模型,输入参数不随时间变化;橡胶悬置通过Bushing单元模拟,只考虑3个平动方向的刚度和阻尼;车架为刚体模型。以下研究的牵引车动力总成通过4点平置、左右对称橡胶悬置支撑,质量M和惯性参数Iij见表1,动力总成质心坐标和悬置位置坐标见表2。

表1 动力总成质量和惯性参数
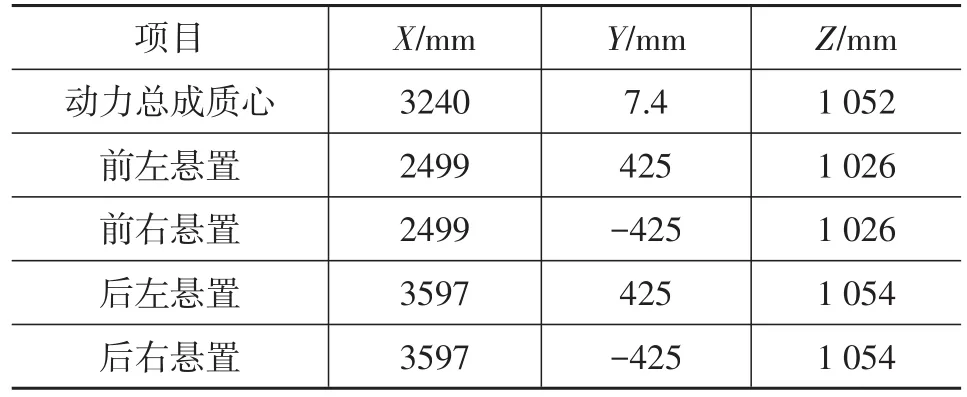
表2 动力总成质心位置和悬置坐标
对于同一橡胶悬置软垫,随着频率增加,其动刚度值相应增加,在低频段动刚度随频率变化较快,在高频段变化较平缓;振动动态幅值越大,动刚度越小;振动动态幅值越小,动刚度值越大[1]。一般来说,动刚度大于静刚度,动静比在1.2-3之间,有些可能会大于3,通过试验测得静刚度(Ku、Kv、Kw)及动刚度系数见表3。
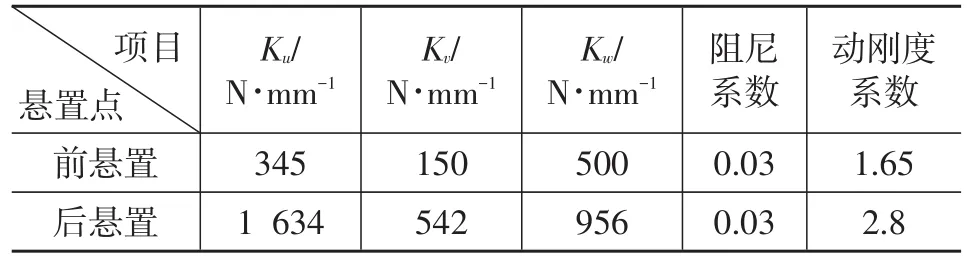
表3 悬置元件参数
通过计算得到动力总成系统沿各方向的固有频率和模态能量分布百分比如表4所示。从表4可以看出,系统固有频率绕X轴的旋转频率最大,最大值28.5 Hz,超出目标值21.2 Hz,接近发动机的激励频率;模态能量相互耦合,解耦率普遍较低。因此认为悬置匹配不合理和模态耦合是引起整车怠速振动较大的主要原因。

表4 动力总成固有频率和模态能量分布
3.2 模态测试
本文采用LMS公司的锤激法(Impact Testing)进行测试得到频响函数(FRF),然后使用Modal Analysis模块对得到的FRF数据进行分析处理,通过Polymax方法进行识别得到悬置系统的固有频率及对应振型。为了更直观查看动力总成6个自由度的振型,使用8个三向加速度传感器成矩形布置在发动机缸体表面,见图3。由于操作空间限制,考虑到发动机的激励主要在Z向和绕X的旋转,因此捶击激励施加在Z向和Y向,激励点选择在传感器附近[2-3]。
由于悬置系统是搭载整车上进行测试而非台架上,车架在这个区间也存在部分模态频率,在模态数据分析过程中需要剔除车架振动的影响。消除干扰频率后,测试得到系统固有频率见表5,对应的振型见图4。测试过程中,测试方案的激励在X向的响应并不明显,在数据分析中没有识别到X向固有频率和振型。从结果对比可以看出,计算结果与测试结果趋势一致;Rx方向模态和测试结果比较接近,因此,使用该模型对悬置系统进行优化可行。
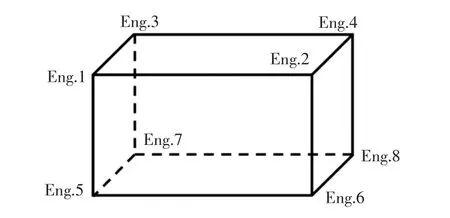
图3 传感器布置
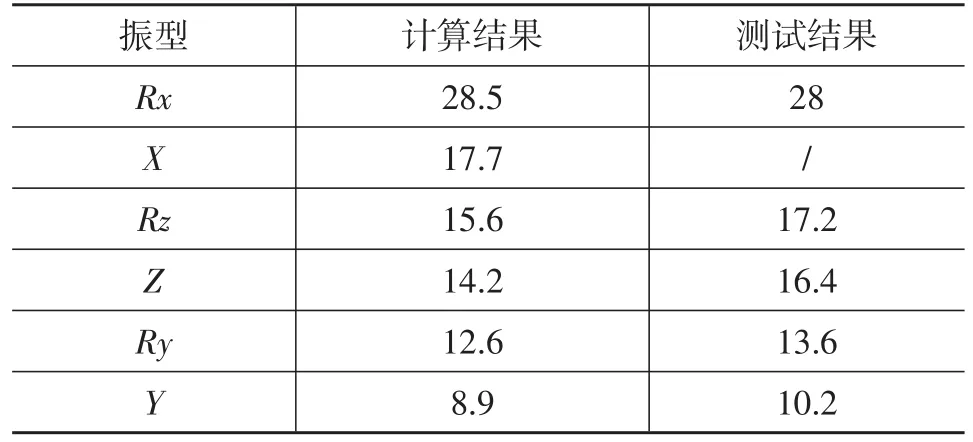
表5 计算结果和测试结果对比 Hz
3.3 系统优化分析
动力总成悬置系统优化一般通过选择合适的悬置刚度、合理的悬置布置位置及合适的布置角度,使系统固有频率远离发动机激励,同时降低各模态之间耦合程度,最终使发动机振动传到车架上的振动达到最小。
a.优化变量设定
考虑到动力总成的安装位置、布置空间的限制、成本及开发时间的限制,悬置系统近似成对称布置,因此选取前、后悬置参数为优化参数。

图4 固有频率及振型
b.优化目标设定
基于能量理论,悬置系统作j阶模态振动时,第k个广义坐标的能量表示为:
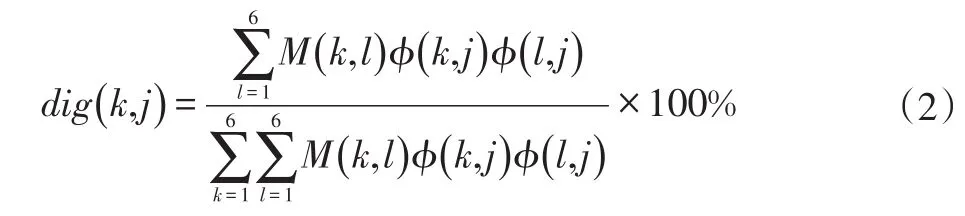
以动力总成悬置系统主振动能量分布的某种组合作为优化设计的目标函数,如下:
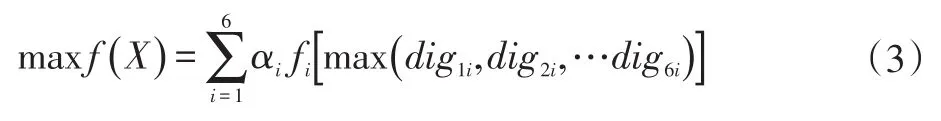
c.约束条件设定
根据上述系统评价要求,系统在6个方向的固有频率必须在5-21.2Hz之间。
d.优化分析
利用ADAMS的优化工具,采用序列二次规划法SQP算法,以悬置系统振动能量解耦程度最大为优化目标,对其进行优化[4-5],优化后悬置刚度参数见表6。
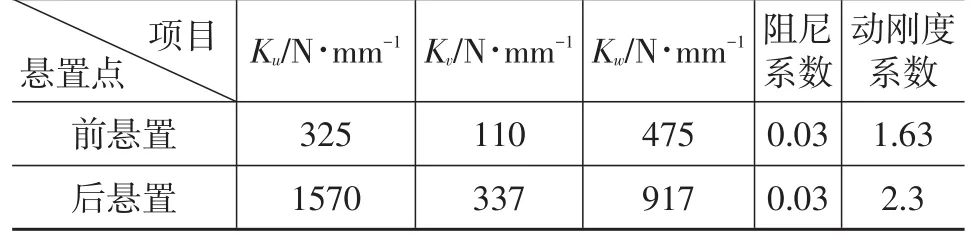
表6 优化后的悬置刚度参数
使用优化后的悬置刚度参数进行模态分析,得到系统的固有频率和模态能量分布见表7。
从表7可以看出,绕X轴(Rx)的能量达到96.3%解耦率很高;模态能量分布在Z向和俯仰方向(Ry)存在耦合,但在Z方向的主振动能量达到66%,考虑到固有频率远离发动机激励频率,可以接受;其它方向模态解耦程度较高。系统各阶模态的固有频率均满足频率匹配要求(5-21.2 Hz)。总体来说,优化后的计算结果基本满足设计要求。
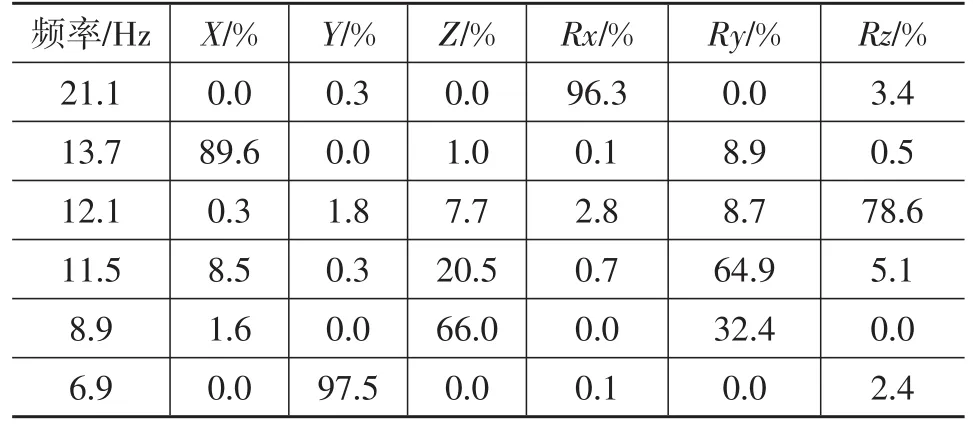
表7 优化后的固有频率和模态能量分布
4 整车性能测试评估
4.1 转向盘的测试结果对比
为了更好的评估动力总成悬置系统优化前、后对整车性能的影响,在整车怠速下对转向盘进行主观评估和振动测试,测试布点在转向盘回正后12点位置。
测试得到的动力总成悬置系统优化前、后转向盘在怠速下振动加速度均方根值如图5所示。从图5可以看出,优化后加速度明显降低,说明动力总成悬置系统优化可有效改善整车振动。
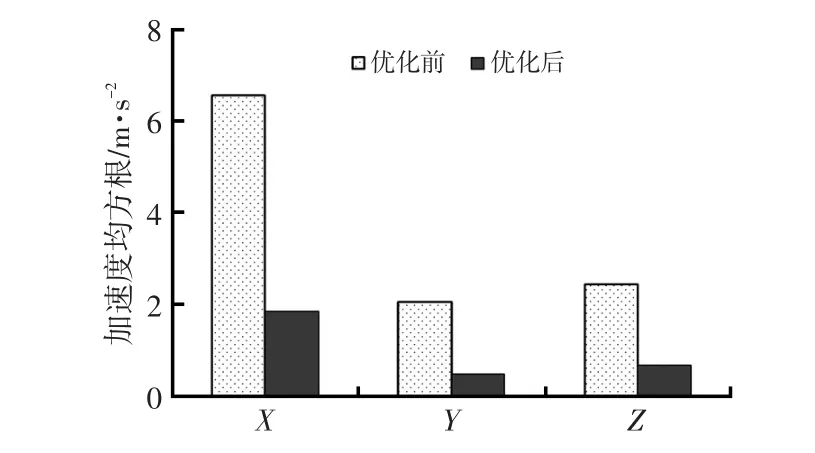
图5 怠速工况下转向盘优化前、后结果对比
4.2 优化前、后悬置传递率对比
为了评估悬置系统隔振性能,对优化前、后悬置点的振动传递率进行测试,如表8所示。从表8中可以看出,悬置参数优化后,传递率明显降低,有效改善了发动机激励向整车的传递。
5 结束语
针对某牵引车使用铝壳代替铸铁壳变速器,动力总成升级后出现怠速工况振动较大问题,利用ADAMS软件对悬置系统刚体模态进行了仿真分析,得到以下结论:
a.分析了引起整车怠速振动的原因,提出了优化方向;
b.通过模态试验验证了仿真模型的有效性,并给出了优化后的悬置参数;
c.在怠速工况下,通过对优化前、后转向盘振动量和悬置传递率进行测试和主观评估表明,优化后整车振动得到明显改善。
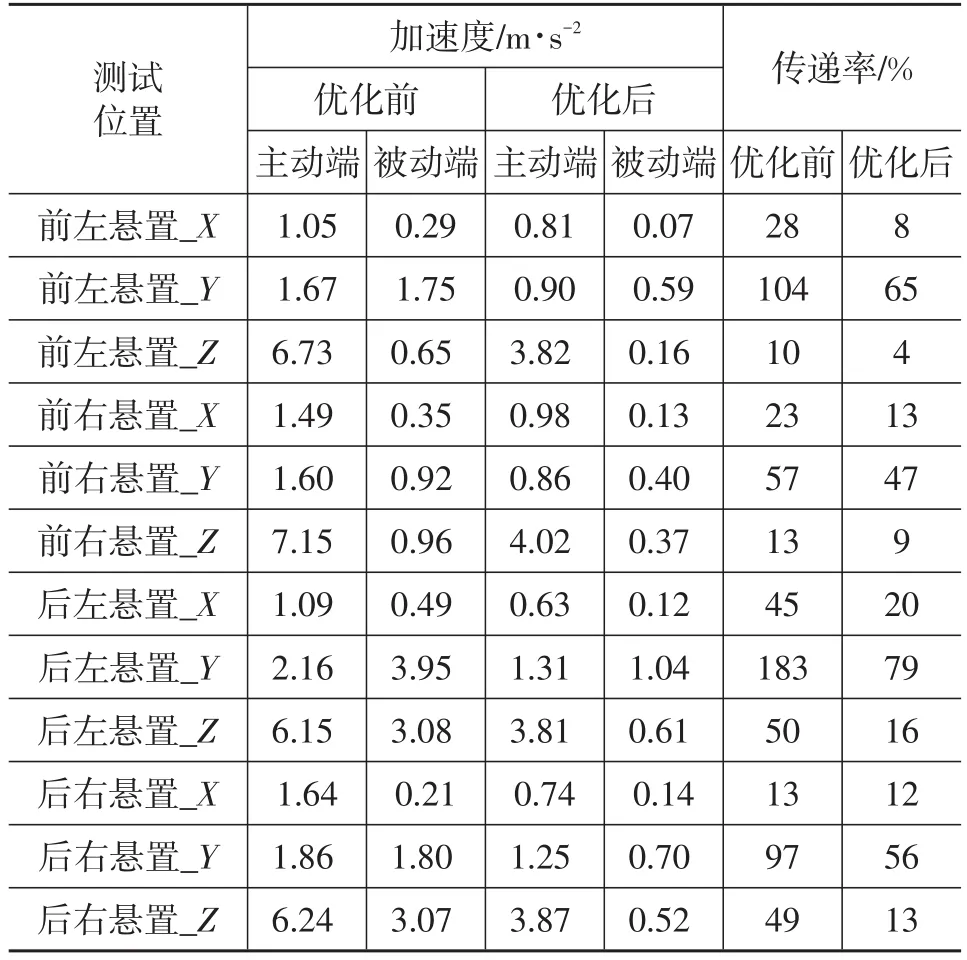
表8 不同悬置位置的振动传递率
[1]刘祖斌,刘英杰.发动机悬置设计中的动、静刚度参数研究.汽车技术,2008(6):21-23.
[2]刘习军,贾启芬.工程振动理论与测试技术.北京:高等教育出版社,2006.
[3]张武,陈剑,陈鸣.汽车动力总成悬置系统多工况运行模态试验研究.中国机械工程,2013(22):3118-3123.
[4]陈大明,上官文斌.动力总成悬置系统刚体模态优化设计方法的研究.汽车技术,2011(2):34-38.
[5]Boggs P.T.and Tolle J.W.Sequential Quadratic Programming.Acta Numerica 1996:1-52.
