混联式混合动力汽车高速工况经济性研究
2018-03-07周文太王晨赵治国于海生张彤
周文太 王晨 赵治国 于海生 张彤
(1.同济大学,上海 201804;2.科力远混合动力技术有限公司,上海 201501)
1 前言
由于越来越多的消费者短途选择纯电动汽车,远行选择混合动力汽车,因此有必要优化混合动力汽车的高速工况经济性。为此,本文针对混联式混合动力汽车高速工况经济性,综合考虑发动机比油耗、电机功率损耗、电池功率损耗,提出一种基于穷举法[1]的经济性最优工作点设计方案,并进行了转毂试验验证。
2 混联式混合动力系统建模
混联式混合动力系统包括混合动力变速器、发电机、电机MG1、电机MG2、动力电池,对各零部件分别建模。
2.1 混合动力变速器模型
混合动力变速器的结构如图1所示,采用双行星排结构,双行星排共用齿圈和行星架,其中齿圈R连接到输出轴OUT,行星架PC经扭转减振器TSD连接到发动机ENG,太阳轮S1连接到小电机MG1,太阳轮S2连接到大电机MG2。混合动力变速器还拥有两个制动器,分别为与行星架相连的制动器B1以及与太阳轮S1相连的制动器B2。

图1 混合动力变速器结构
双行星排运动部件的转速关系[1~3]为:
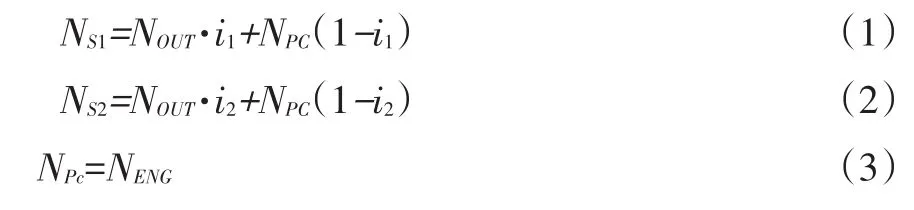

式中,i1、i2分别为前、后行星排传动比;NOUT、NPC、NS1、NS2、NENG、NMG1、NMG2分别为齿圈R、行星架PC、太阳轮S1、太阳轮S2、发动机、电机MG1和电机MG2的转速。
双行星排运动部件的扭矩关系[1~3]为:


式中,aS1、aS2、aPC分别为太阳轮S1、太阳轮S2、行星架PC的角加速度;TS1、TS2、TPC和TOUT分别为作用在太阳轮S1、太阳轮S2、行星架PC以及齿圈R上的转矩;TMG1、TMG2、TENG分别为电机MG1、电机MG2、发动机输出的转矩;JS1、JS2、JPC分别为太阳轮S1、太阳轮S2、行星架PC的转动惯量。
2.2 发动机模型
发动机万有特性如图2所示。
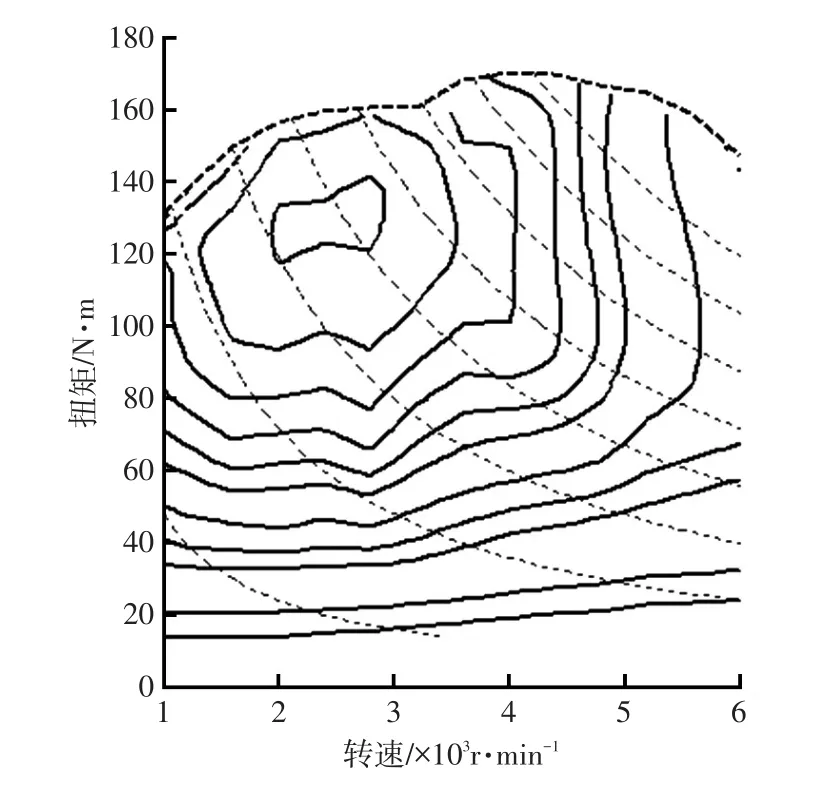
图2 发动机万有特性
通过查发动机万有特性二维表格,利用式(8)求得发动机比油耗be:
2.3 电机MG1模型
电机MG1的效率特性曲线如图3所示。
电机MG1的理论用电功率和实际用电功率计算式为:

式中,PMG1_ideal为电机MG1的理论电功率;ηMG1为电机MG1的效率;PMG1为电机MG1的实际电功率。
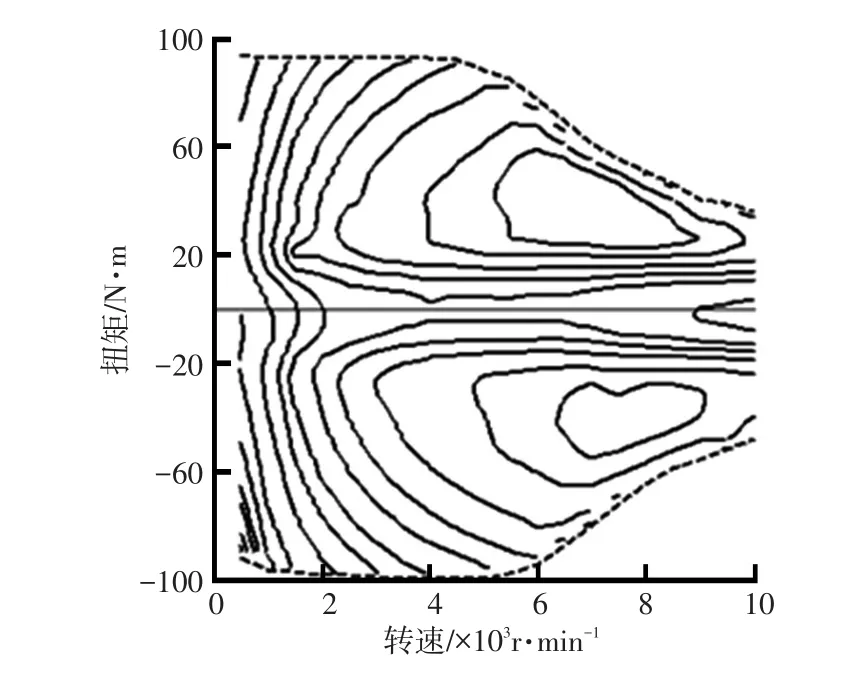
图3 电机MG1特性曲线
2.4 电机MG2模型
电机MG2的效率特性曲线如图4所示。
图4 电机MG2特性曲线
电机MG2的理论用电功率和实际用电功率计算式为:

式中,PMG2_ideal为电机MG2的理论电功率;ηMG2为电机MG2的效率;PMG2为电机MG2的实际电功率。
2.5 动力电池模型
假设电池温度处于合理范围、电池处于健康状态,只考虑电池内阻造成的电功率损耗,则电功率损耗计算式为:

式中,Pb为动力电池总用电功率;U为电池电压;Pb_loss为电池的电功率损耗;I为电池电流;rb为电池内阻。
2.6 整车动力学模型
由车辆动力学可得:

假设车辆在平直路面匀速行驶,则整车行驶阻力[4]为:

式中,V为车速;r为车轮半径;i为主减速比;Fresi为整车行驶总阻力;G为作用于整车的重力;f为滚动阻力系数;CD为空气阻力系数;A为迎风面积。
3 高速工况油耗分析
3.1 高速工况百公里油耗计算
在车速为V的高速工况下,特定的发动机工作点NENG、TENG对应的整车百公里油耗Q的计算方法如下:
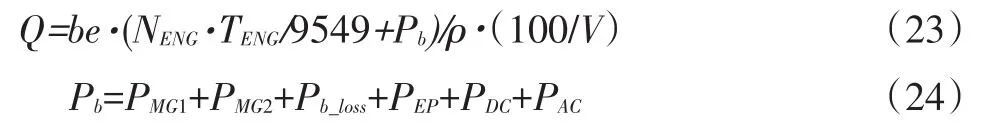
式中,PEP为电子油泵用电功率;PDC为DC用电功率,PAC为空调用电功率;PEP、PDC、PAC均从整车CAN网络上获取;ρ为燃油密度。
式(24)中,PMG1、PMG2、Pb_loss通过式(1)~式(5)和式(12)~式(19)计算得到。
3.2 经济性最佳工作点的确定
在各车速下,基于穷举法,列出所有允许的NENG、TENG组合,根据上述公式计算得到所有NENG、TENG组合对应的百公里油耗。做取小运算得到各NENG下的最经济百公里油耗,以NENG为横轴,各NENG下最经济百公里油耗为纵轴,得到二者特性关系如图5所示。
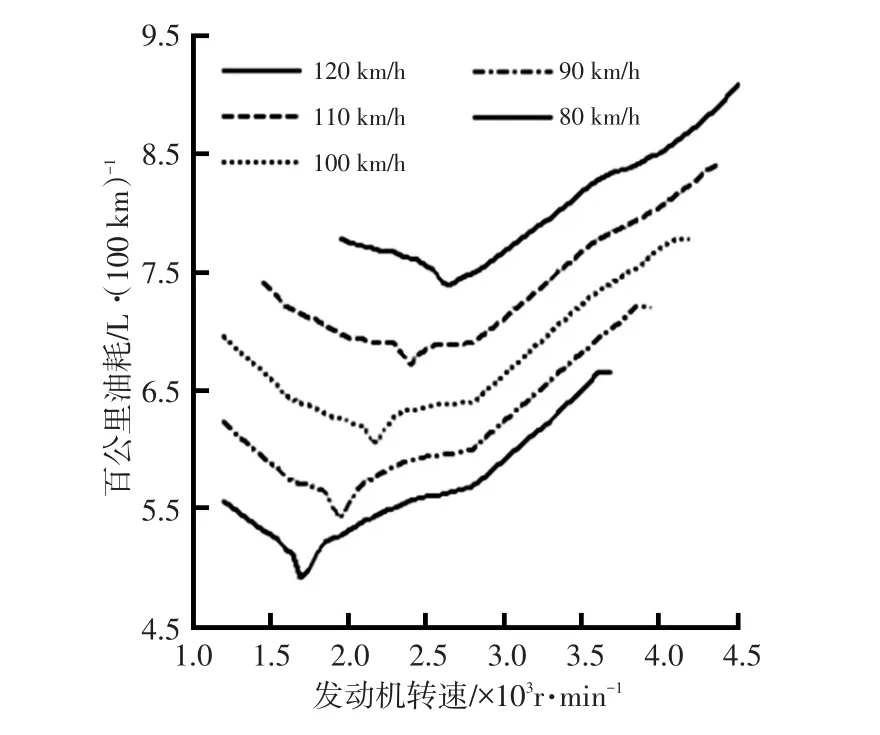
图5 发动机转速与百公里油耗特性
由图5可知,各车速下均能找到一个百公里油耗最经济的发动机转速,且该发动机转速与车速呈线性关系。图6为各车速下的最经济发动机转速以及对应的发动机扭矩、电机MG1转速、电池功率,由图6可知,最经济发动机转速对应的电机MG1转速为0,说明系统工作在制动器B2锁止的混合动力模式。B2锁止混合动力模式的系统杠杆关系[4]如图7所示。
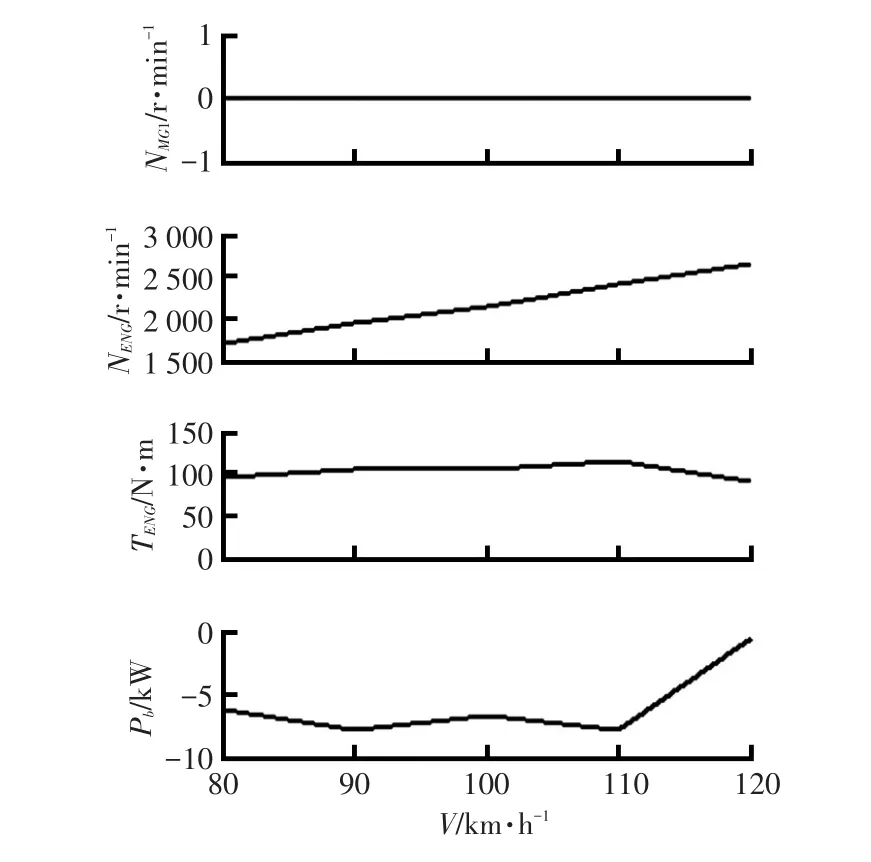
图6 经济性最佳发动机工作点及电池功率特性

图7 制动器B2锁止的混合动力系统杠杆图
制动器B2锁止时,电机MG1转速固定为0,发动机转速及电机MG2转速随输出轴转速的上升而线性上升,相当于固定速比传动。
3.3 不充不放模式下最佳工作点的确定
图6显示系统工作在经济性最优工作点时,电功率为负,即系统向电池充电。本文所研究的混合动力汽车匹配6 Ah的镍氢电池,如果以6 kW的功率给电池充电,则只需要5.4 min即可将电池SOC从0.4充电至0.7,达到电池常用SOC上限,所以不能一直向电池充电。
为此,采用两段式控制策略,在SOC低于阈值0.7时,控制系统工作在经济性最优模式向动力电池充电;当SOC达到指定的阈值后切换到不充不放模式,以避免电池过充。采用两段式策略可在高速工况将电池充电到SOC较高状态,使得车辆离开高速、进入城郊工况时拥有较长的纯电续航里程,从而不仅在高速工况经济性较佳,也有助于在城郊工况获得较好的经济性。
在各车速下,采用穷举法,限制电池用电功率为0.1 kW以内,计算所有允许的发动机工作点对应的百公里加速油耗,得到不充不放模式下最佳发动机工作点如图8和图9所示。由图8和图9可知,不充不放模式系统工作在B2锁止点经济性最佳。

图8 不充不放模式下发动机转速与百公里油耗特性
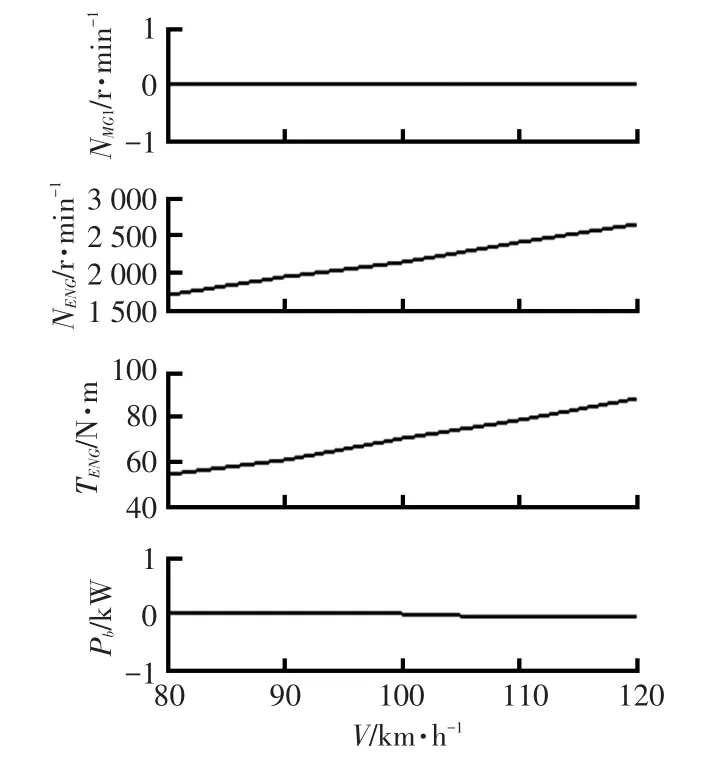
图9 不充不放模式下发动机工作点及电池功率特性
图9与图6的发动机扭矩曲线差距较大,图6发动机扭矩稳定工作在100 N·m左右,而图9发动机扭矩随车速的上升而上升。原因是不充不放模式下电池功率需在零附近,所以发动机扭矩与整车行驶阻力呈线性关系。
3.4 锁止点附近发动机比油耗及电机功率损耗分析
以不充不放模式、车速为110 km/h为例,分析制动器B2锁止点附近的比油耗及电机功率损耗变化规律。
图10为发动机扭矩及比油耗的变化规律,图中虚线为锁止点。在锁止点左侧,随发动机转速的上升,发动机扭矩从150 N·m开始逐渐下降,在扭矩为120~135 N·m范围比油耗达到最佳的240 g/kW·h,然后,随发动机转速上升、扭矩下降,比油耗逐渐上升;在锁止点处,比油耗为257 g/kW·h;在锁止点右侧,比油耗随发动机转速的上升而恶化。

图10 发动机扭矩及比油耗变化规律
图11为电机MG1工作点及功率损耗的变化规律,图中虚线为锁止点。在锁止点左侧,随发动机转速的上升,MG1转速与扭矩绝对值均下降,MG1功率及功率损耗也随MG1转速逼近锁止点而下降;在锁止点,MG1进入Standby状态,功率损耗为0;在锁止点右侧,随发动机转速的上升,MG1转速上升、扭矩下降,功率缓慢上升,功率损耗也随之缓慢上升。
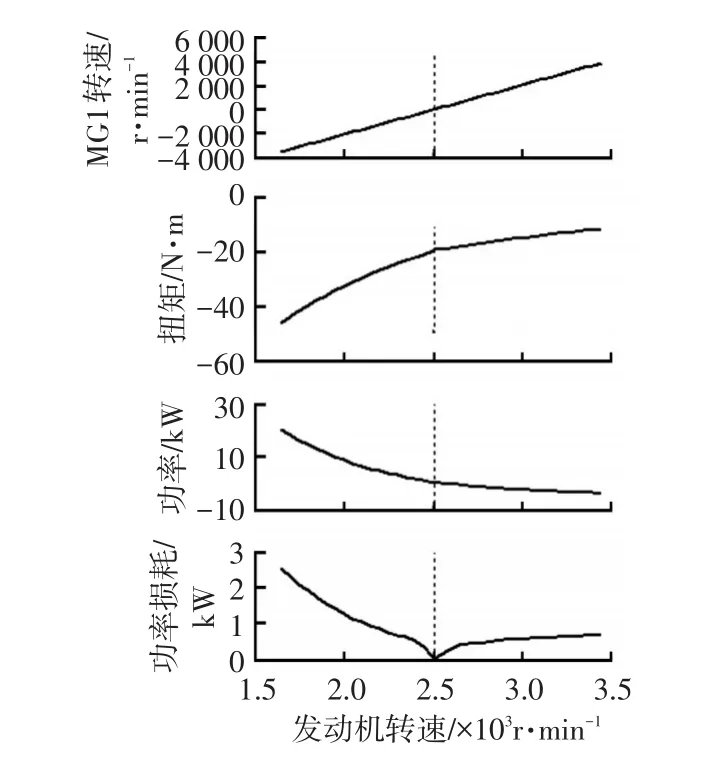
图11 电机MG1工作点及功率损耗
图12为电机MG2工作点及功率损耗的变化规律,图中虚线为锁止点。在锁止点左侧,随发动机转速的上升,MG2转速与扭矩绝对值均下降,因而MG2的功率绝对值以及功率损耗也随着逼近锁止点而下降;在锁止点,MG2进入停止工作状态,功率损耗为0;在锁止点右侧,随发动机转速的上升,MG2转速下降、扭矩上升,功率缓慢上升,功率损耗也随之缓慢上升。
综合前述分析,在锁止点虽然发动机比油耗并非最佳,但电机MG1、电机MG2功率损耗为0,在锁止点混合动力系统经济性最优。
4 转毂试验验证
如前所述,在经济性最优模式下只需5.4 min即可将电池充电到常用的SOC上限并切换到不充不放模式。在高速工况下,除最初几分钟外,系统均工作在不充不放模式,所以针对不充不放模式的百公里油耗进行试验验证。
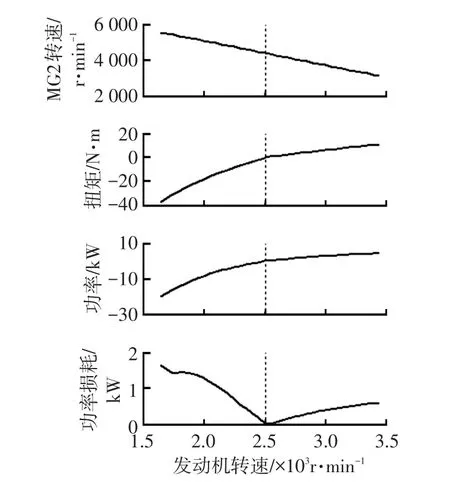
图12 电机MG2工作点及功率损耗
如图13和图14所示,不充不放模式下经济性最佳工作点对应的电机MG1转速为0,说明混合动力系统工作在制动器B2锁止模式经济性最佳。图13与图8在发动机转速为80 km/h和90 km/h时有一些差距,原因是整车的发动机实际比油耗与通过台架试验得到的发动机万有特性有一定的差距。
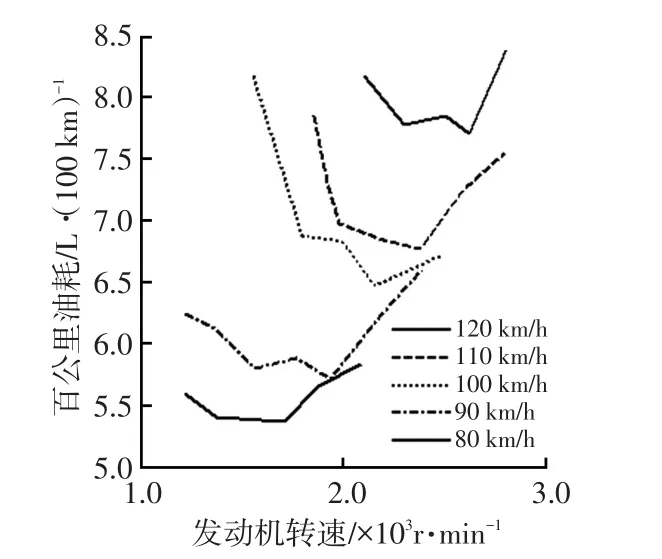
图13 不充不放模式下发动机转速与百公里油耗试验结果

图14 不充不放模式下发动机工作点及电池功率试验结果
5 结束语
针对混联式混合动力汽车的高速工况经济性,综合考虑发动机比油耗、电机功率损耗、电池损耗,提出一种基于穷举法的经济性最佳工作点设计方案。通过转毂试验表明,各车速下基于穷举法设计的发动机工作点百公里油耗优于其它发动机工作点,本文的研究对同类的混联式混合动力汽车改善高速工况经济性具有一定的参考价值。
[1]吴迪,于明志.利用穷举搜索法准确确定地下热物性参数[J].工程热物理学报,2017,38(04):822-827.
[2]HaishENG Yu,Jianwu Zhang,TongZhang.Control strategy design and experimental research on a fourshaftelectroniccontinuouslyvariabletransmission hy⁃brid electric vehicle.Proceedings of the Institution of Mechanical ENGineers,Part D:Journal of Automobile ENGineering.2012,226:1594-1613.
[3]王晨,赵治国,张彤,等.复合功率分流式e-CVT结构优化及验证[J].中国公路学报,2015,28(3):117-126.
[4]刘钊,赵世琴,黄宗益.用杠杆模拟法建立行星变速器动力学模型[J].汽车工程,2000,22(4):274-277.
