一种求解二维矩形Packing问题的拟人型全局优化算法
2018-03-06邓见凯尹爱华
邓见凯,王 磊,尹爱华
(1.武汉科技大学计算机科学与技术学院,湖北 武汉 430065;2.智能信息处理与实时工业系统湖北省重点实验室,湖北 武汉 430065;3.江西财经大学软件与通信工程学院,江西 南昌 330013)
1 引言
二维矩形Packing问题是指:在二维欧氏空间中,给定1个矩形容器和n个矩形块。矩形容器和矩形块的长、宽为已知的正实数。在满足三个约束条件的前提下,要求将这些矩形块放入矩形容器内,使得矩形容器的面积利用率最大化。约束条件为:第一,小矩形块须完全在矩形容器内。第二,矩形块的每条边均和矩形容器的某条边平行或重合。第三,每两个小矩形块相互不重叠。三个约束条件可简称为:“不出界、不倾斜、不重叠”。
W和H表示矩形容器的长度和宽度。wi和hi表示矩形块Ri的长度和宽度。(xli,yli)和(xri,yri)分别表示矩形块Ri被放入矩形容器后,其左下角和右上角的坐标。若矩形块Ri已被放入矩形容器中,则逻辑变元pi值为1;否则pi值为0。矩形容器位于第一象限,并且其左下角位于坐标原点(如图1所示)。二维矩形Packing问题的形式化描述如下:
subject to
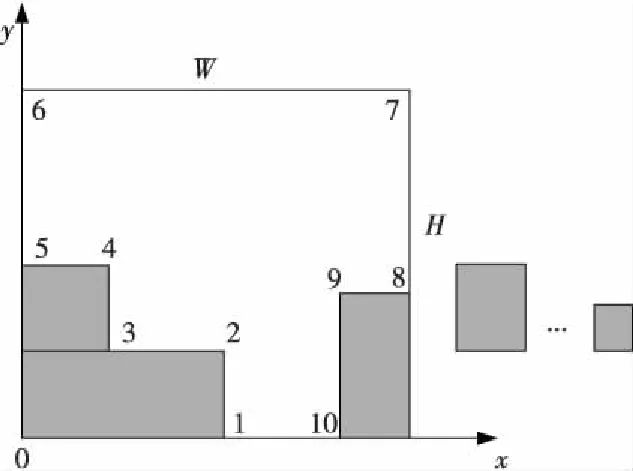
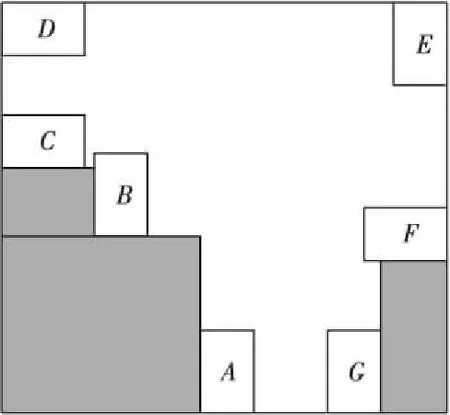
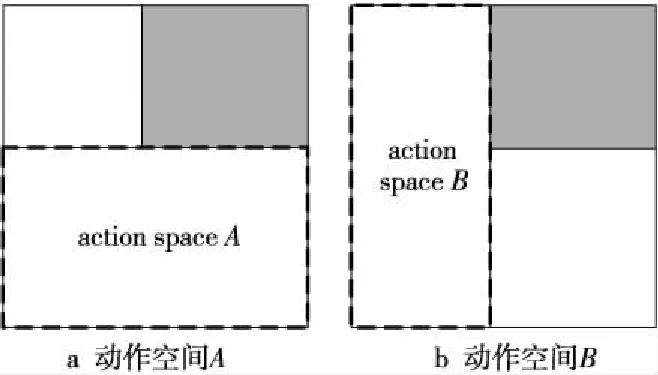
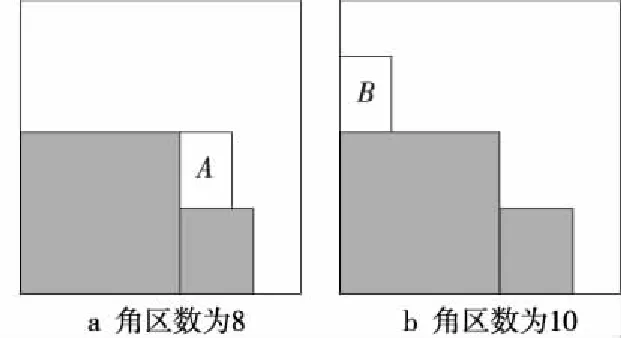
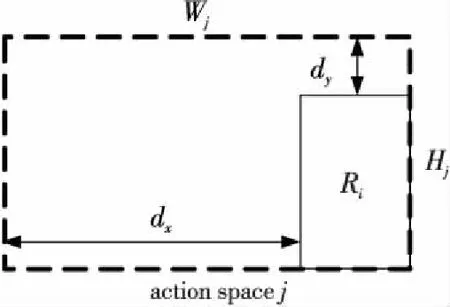
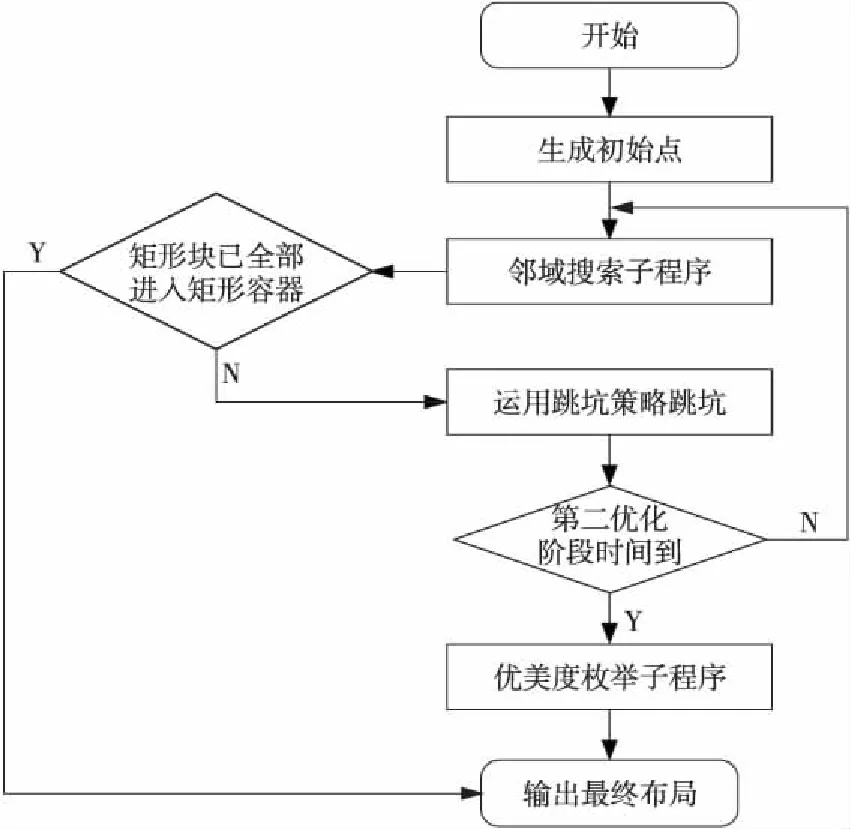
pi=0∨(0≤xli (1) pi=0∨(xri-xli=wi∧yri-yli=hi)∨(xri-xli=hi∧yri-yli=wi) (2) pi=0∨pj=0∨(xli≥xrj∨xlj≥xri∨yli≥yrj∨ylj≥yri) (3) pi∈{0,1} (4) 其中,i,j=1,2,…,n,并且i≠j。公式(1)表示每个小矩形块须完全在容器内。公式(2)表示小矩形块的每条边均和矩形容器的某条边平行或重合。公式(3)表示每两个小矩形块相互不重叠[1]。 二维矩形Packing问题已被证明为NP难度问题。工商业、运输、物流领域的诸多问题可归结为二维矩形Packing问题。例如,在板材切割加工过程中,需要合理布局以提高材料利用率;在集成电路设计中如何布置以提高布局空间利用率[2]。 算法可分为完整算法和启发式算法两类。完整算法能保证找到最优布局,但是所花时间太长,仅可用于计算较小规模的问题实例[3]。启发式算法又可分为非随机型算法和随机型算法。 非随机型算法着力于提出选择放置动作的优先序,并在其基础上进行树搜索,包括底部左齐择优匹配算法[4]、分支限界[5]、拟人算法[6-10]。文献[6]提出基于动作空间的基本算法和增强算法。动作空间定义的引入便于计算出合理的占角动作。基本算法在多个占角动作中选择时,优先选取与当前动作空间相贴边多、对剩余空间损害小、与其它已放入块关系更紧密的动作。增强算法在每一步考察优先序中排名前N名的占角动作,通过向前看并回溯的方法选择一个动作。 随机型算法以矩形块优先序作为高维空间中的点,设计各种邻域结构,结合了各种紧密放置矩形块的策略以及搜索策略,包括贪心随机适应搜索算法[11]、模拟退火和贪心局部搜索算法[12]、禁忌搜索算法[13]、随机局部搜索[14,15]、变邻域搜索[16]。 为实现全局优化,本文中的算法主要采用两种方法。第一是采用三阶段优化,结合了目前文献中非随机型和随机型算法的优点。第二是提出跳坑策略将搜索引向有希望的区域。 定义1(格局) 矩形容器内已放入一些矩形块,每个矩形块的位置、方向已知,容器外尚有矩形块待放,这称为一个格局。初始格局中,所有矩形块均在容器外。终止格局中,所有矩形块均在容器内,或者虽有块在容器外但已经不可能再放入。图1为一个格局[17]。 Figure 1 Configuration and corner areas图1 格局及角区 定义2(角区) 矩形容器中由块或者矩形容器本身形成的直角形状的空白区域被称为角区。分为90°角区和270°角区。图1中有10个角区,其中角区1、3、5、6、7、8、10为90°,角区2、4、9为270°。角区的定义来自于人们装箱的实际经验。将物体放在角区,在格局中腹部留出大片相对完整的空白区域,有利于后续矩形块的布局。本文与文献[17]中的角区定义有所不同。本文中的角区全部为“实角”。也就是说,角区的顶点一定是某个小矩形块(或矩形容器)的顶点。这样设计的优点是布局更为紧密。 定义3(占角动作) 在满足三个约束条件的前提下,将一个矩形块按照指定方向(站或躺)放在指定的位置(用块左下角坐标表明),使得矩形块的一角正好与90°角区的角重合。这称为一个占角动作。图2中A、B、C、D、E、F、G均为占角动作。 Figure 2 Corner-occupying action图2 占角动作 定义4(动作空间) 在当前格局下,若往矩形容器内放入一个虚拟的矩形块(满足三个约束条件),使得该块的上下左右四条边均与其它已放入的块或容器的边相贴(重合的长度大于0),则该虚拟块所占的空间称为当前格局下的一个动作空间[9,11]。初始格局下,恰有一个动作空间,当放入一个矩形以后,形成两个动作空间,如图3所示。动作空间的定义有助于计算矩形块的合理动作。 Figure 3 Action space图3 动作空间 定义5(剩余空间平整度) 平整度计算公式为e4-m,其中m为剩余空间的角区数(包括90°和270°角区)。剩余空间的角区数越少,其平整度越高,有利于放置后续矩形块。图4a中,将矩形块放在位置A,剩余空间m值为8。图4b中,将同一个矩形块放在位置B,则剩余空间m值为10。因此,图4a中的剩余空间平整度较高。本文对文献[6]中的平整度定义作了简化。 Figure 4 Degree of planeness图4 剩余空间平整度 定义6(占角动作的重叠度) 一个占角动作所对应的矩形块与其所在动作空间的贴边数,称为其重叠度。重叠度高的动作,与所在动作空间贴合较好,对剩余空间损害较小,有利于放置后续矩形块[7]。图5a和图5b中动作重叠度分别为3和2。 Figure 5 Degree of overlapping of the corner-occupying action图5 占角动作重叠度 Figure 6 Degree of cave of the corner-occupying action图6 占角动作穴度 定义8(占角动作面积利用率) 占角动作面积利用率的计算公式为(wihi)/(WjHj)(参见图6)。 定义9(占角动作的浪费度) 当一个占角动作做完后,在其占据的动作空间中最多可能生成两个新的动作空间(参见图7)。若一个新的动作空间过小,放不下矩形容器外的任何一个小矩形块,则称其为被浪费的动作空间。占角动作做完后新生成的被浪费的动作空间的数量,称为此占角动作的浪费度。观察图7a和图7b中的两个新生成的动作空间。若两个动作空间均为被浪费的动作空间,则占角动作的浪费度为2;若其中恰有一个动作空间被浪费,则占角动作的浪费度为1;否则占角动作的浪费度为0。 Figure 7 Degree of waste of the corner-occupying action图7 占角动作浪费度 定义10(矩形块优先级) 假定n个矩形块分为k种形状大小两两不等的类型,矩形块的优先级是1~k的正整数。对于形状大小相同的矩形块,其优先级相等。不妨令k级为最高优先级,1级为最低优先级。w(Ri)表示矩形块Ri的优先级,1≤w(Ri)≤k。 定义11矩形块排序的3项指标:(1) 矩形块的周长,大优先;(2) 矩形块的长边长,大优先;(3)矩形块的序号,小优先。对矩形块排序后,在查找时可利用折半查找,提高速度。 定义12占角动作排序的9项指标:(1) 动作做完后,矩形容器内剩余空间的平整度,大优先;(2) 动作的重叠度,大优先;(3) 矩形块的优先级,大优先;(4) 动作的穴度,大优先;(5) 动作的浪费度,小优先; (6) 矩形块的序号,小优先;(7) 矩形块左下顶点的y坐标,小优先;(8) 矩形块左下顶点的x坐标,小优先;(9) 矩形块的方向,躺优先。 定义13动作空间排序的4项指标:(1) 动作空间左下角的x坐标,小优先;(2) 动作空间左下角的y坐标,小优先;(3)动作空间的长度,小优先;(4)动作空间的宽度,小优先。 如果某个动作空间放不下任何一个容器外的矩形块,则在动作空间序列中删去此动作空间。对动作空间排序后,为节省计算时间,本文仅考虑排序前M位的动作空间。M取值为200。 基本算法命名为A1算法。其步骤如下: Step1初始格局:所有矩形块均在矩形容器外,矩形容器是空的。依字典序按照矩形块排序的3项指标(见定义11)对所有矩形块排序。 Step2在当前格局下,依字典序按9项指标(见定义12)选择最优先的占角动作来做,动作做完以后,演化到新格局。 Step3对动作空间序列做如下三步操作。第一,更新占角动作所在的动作空间。第二,检查所放入的矩形块是否与动作空间序列中其它动作空间重叠。若有重叠,则更新重叠的动作空间。第三,删去被其它动作空间包含的动作空间。 依此类推,循环做Step 2~Step 3,直到终止格局为止。 整个拟人型全局优化算法由三个优化阶段组成(参见图8)。拟人型全局优化算法基于基本算法A1和优美度枚举子程序B1,因此本文将拟人型全局优化算法命名为A1B1算法。 Figure 8 Sketch of the whole algorithm图8 算法总体框图 (1)在第一优化阶段中生成初始点(2.4节)。初始点记为Q0,它表示所有矩形块的初始优先级。给定Q0后,从初始格局出发,运用基本算法A1可唯一确定一个终止格局。这个终止格局记为C(A1,Q0)。 (2)在第二优化阶段中,交替循环调用邻域搜索子程序(2.5节)和跳坑策略子程序(2.6节),针对所有矩形块的优先级进行优化。调用邻域搜索子程序。若发现矩形块已全部进入矩形容器,则成功停机。若搜索遇到局部最优点,则调用跳坑策略子程序跳出局部最优点,得到新的起点。从新起点开始,又循环调用邻域搜索子程序。如此反复,直到满足第二阶段计算停止条件为止。 第二优化阶段结束时,得到一个优化后的所有矩形块的优先级,记为Q+。根据Q+,从初始格局出发,运用基本算法A1可唯一确定一个终止格局。这个终止格局记为C(A1,Q+)。 (3)在第三优化阶段中调用优美度枚举子程序(2.7节)。优美度枚举子程序命名为B1算法。B1算法是一种树搜索程序,针对占角动作的选择进行优化。从初始格局出发,按照优先级Q+,B1算法可唯一确定一个终止格局。这个终止格局记为C(B1,Q+)。 每个优化阶段的计算停止条件均为两个:第一个条件是当矩形块已全部进入矩形容器,则输出布局,成功停机。第二个条件是计算达到本阶段的计算时间上限,则停止,转入下一个优化阶段。本文中三个优化阶段的时间上限相等。 若三个优化阶段结束,仍未将所有矩形块放入矩形容器,则输出计算历史上所生成的最优布局,停机。 小规模实例(矩形块数小于或等于200)、中规模实例(矩形块数大于200且小于或等于500)、大规模实例(矩形块数大于500且小于或等于10 000)、对超大规模实例(矩形块数大于10 000)的计算时间上限分别为360 s、600 s、1 200 s和15 000 s。 所谓生成初始点,是指对所有矩形块指派优先级。本文按照大矩形块优先的策略指派优先级,有“周长大者优先”“面积大者优先”“长边长大者优先”三种具体做法。第一种做法:首先按照定义11对所有矩形块排序,然后依次指派优先级,这是“周长,大优先”的做法。第二种做法:将定义11中的第1项指标改为“矩形块的面积,大优先”。第三种做法:删去定义11中的第1项指标,这是“长边长,大优先”的做法。三种做法各有其优缺点,本文在其中均匀地随机取一种,生成初始点。 Q=(q(R1),q(R2),…,q(Ri),…,q(Rn))表示所有矩形块的优先级。用Q表示n维空间中的一个点。只要指定Q值,从初始格局出发,运用基本算法A1可唯一确定一个终止格局。这个终止格局记为C(A1,Q)。 以A1算法为基础进行适当的邻域搜索(属于局部搜索),期望寻找更优的矩形块的优先级。本文提出两种邻域结构,一定程度上避免单一型邻域结构的局限性。 定义14(交换式邻域) 任意给定所有矩形块的优先级Q,不妨将矩形块按照优先级从高到低的顺序排列。考虑优先级为k1和k2的矩形块,将它们的优先级互换,保持其余矩形块的优先级不变。从而得到一个新优先级Q′,Q′的集合构成Q的交换式邻域。其中1≤k1 定义15(插入式邻域) 任意给定所有矩形块的优先级Q,将矩形块按照优先级从高到低的顺序排列。考虑所有优先级大于或等于k1并且小于或等于k2的矩形块,插入式邻域有两种方式:第一种是将原优先级为k2的矩形块降为k1级,然后将原优先级严格小于k2并且大于或等于k1的矩形块均升1级。第二种是将原优先级为k1的矩形块升为k2级,然后将原优先级严格大于k1并且小于或等于k2的矩形块均降1级。其余矩形块的优先级不变。 例1已知6个矩形块的优先级:q(R2)=4,q(R4)=3,q(R5)=3,q(R3)=2,q(R1)=1,q(R6)=1。首先讨论交换式邻域。例如考虑优先级为1和3的矩形块,互换其优先级。q(R1)=3,q(R6)=3,q(R4)=1,q(R5)=1,其余矩形块的优先级不变。 然后讨论插入式邻域。例如考虑优先级从2到4的矩形块。可将优先级为4的矩形块降为2级,然后优先级为3和2的矩形块均升1级。新的优先级为:q(R4)=4,q(R5)=4,q(R3)=3,q(R2)=2。也可以将优先级为2的矩形块升为4级,然后优先级为4和3的矩形块均降1级。新的优先级为:q(R3)=4,q(R2)=3,q(R4)=2,q(R5)=2。其余矩形块的优先级不变。 进行邻域搜索时采用“见好就收”的策略以节约计算时间。迭代的一步为:依次考虑当前点Q的全部邻点,对于邻点按照基本算法A1计算出对应的布局。一旦发现某个邻点所对应的布局面积利用率更高,立刻用此邻点取代当前点,一步迭代完成。若所有邻点对应的布局的面积利用率均不高于当前点对应的布局,则当前点为局部最优点,停止本次邻域搜索子程序的运行。 与现有求解矩形Packing问题的文献中的邻域搜索程序[16]相比,本文增加了插入式邻域,使得搜索范围扩大,有利于找到更优布局。 当邻域搜索遇到局部最优点时,调用跳坑策略子程序跳出局部最优点,得到新的起点。从新的起点出发继续进行邻域搜索。如此反复,有望找到更优布局。现有文献主要采用模拟退火、禁忌搜索等方法跳出局部最优。本文采用的是拟人途径跳出局部最优陷阱。 起跳点的选择有两种方式:第一种是回到历史最好点。在第二优化阶段所发现的历史最好点(对应的布局面积利用率最高)的信息可以利用。为避免搜索总是围绕在历史最好点附近,第二种起跳方式是从当前点起跳。本文在两种起跳方式中均匀地随机选择一种。 跳坑方法是对起跳点进行随机扰动。具体做法为R步迭代,每一步迭代是在起跳点的所有邻点中均匀地随机选取1个邻点,将此点作为新的起跳点,从而完成1步迭代。在第4节的实验中,R是在[10,20]内均匀分布的随机整数。 定义16(占角动作优美度) 在当前格局下,定义占角动作的优美度:占角动作做完后,按照基本算法计算到终止格局,终止格局中矩形块的面积之和称为此占角动作的优美度。 优美度枚举子程序采用了棋类游戏中“向前看并回溯”的思路,其具体步骤如下: Step1初始格局。所有矩形块均在矩形容器外。 Step2进行一轮计算:在当前格局下,首先依字典序按照定义12中的9项指标对所有占角动作排序,取排名前N名的占角动作为候选。然后调用A1算法依次计算这N个动作的优美度。最后选择其中优美度最大的动作。若优美度最大的动作有多个,则按照定义12取其中最优先的动作。动作做完后,演化到新格局。 Step3更新动作空间序列。 循环执行Step 2和Step 3,直到算法停机。 停机条件有两个:第一,所有矩形块均已放入矩形容器。第二,优美度枚举子程序的执行时间已经达到所设定的上限。 基本算法A1按照定义12中的9项指标来选取排序第一的占角动作。对定义12中的9项指标略作修改,可得到基本算法族。 基本算法A2:从算法A1修改而来。将定义12中的第(4)项指标和第(5)项指标互换。 基本算法A3:从算法A1修改而来。将定义12中的原第(5)项指标改为第(3)项指标,再将原第(3)、第(4)项指标改为第(4)、第(5)项指标。 基本算法A4:从算法A1修改而来。将定义12中的第(7)项指标和第(8)项指标互换。 基本算法A5:从算法A2修改而来。将定义12中的第(7)项指标和第(8)项指标互换。 基本算法A6:从算法A3修改而来。将定义12中的第(7)项指标和第(8)项指标互换。 基本算法A7~A12分别从算法A1~A6修改而来:将“动作的穴度,大优先”这项指标改为“动作的面积利用率,大优先”。 优美度枚举子程序B1调用基本算法A1进行树搜索。将优美度枚举子程序所调用的基本算法分别替换成Ai,可以得到一个优美度枚举子程序族Bi,其中1≤i≤12。 对于2.3节中的拟人型全局优化算法A1B1来说,它基于基本算法A1和优美度枚举子程序B1,将A1和B1分别替换成Ai和Bi,可得到一个拟人型全局优化算法族AiBi,其中1≤i≤12。 定义17(布局优度) 布局优度是指在矩形容器内的矩形块的面积和。 定理1(优度定理1) 优美度枚举子程序第i+1轮计算所得最优布局的优度高于或等于第i轮计算所得最优布局的优度。 证明从略。 定理2(优度定理2) 第三优化阶段所得布局的优度高于或等于第二优化阶段所得布局的优度。 证明从略。 本文算法是针对二维矩形Packing问题而设计的,也可用于求解二维矩形Strip Packing问题。Strip Packing问题是指:矩形容器的长度W固定,在满足“不出界、不倾斜、不重叠”三个约束条件的前提下,要求用宽度H尽可能小的矩形容器将所有矩形块装入。 除了“不出界、不倾斜、不重叠”以外,很多文献中还可能考虑另外两个约束条件:第一个约束条件是“一刀切”约束;第二个约束条件是关于矩形块的方向:可旋转90°或者方向固定。根据这两个约束条件将二维矩形Strip Packing问题分为如下四个子类:第一,RF子类:矩形块的方向可旋转90°,不考虑“一刀切”约束。第二,RG子类:矩形块的方向可旋转90°,考虑“一刀切”约束。第三,OF子类:矩形块的方向固定,不考虑“一刀切”约束。第四,OG子类:矩形块的方向固定,考虑“一刀切”约束。 本文算法用于计算OF子类。算法计算了6组benchmark问题实例:(1)C组(21个实例),由Hopper和Turton[18]提出;(2)N组(13个实例),由Burke[19]等人提出;(3)NT组(70个实例),由Hopper和Turton[18]提出;(4)CX组(7个实例),由Ferreira和Oliveira[20]提出;(5)2SP组(38个实例),其中cgcut1-cgcut3由Christofides和Whitlock[21]提出,gcut1-gcut13和ngcut1-ngcut12由Beasley[22]提出,beng1-beng10由Bengtsson[23]提出;(6)ZDF组(16个实例),由Riff等人[24]、Leung和Zhang[12]提出。 本文使用拟人型全局优化算法族来计算二维矩形Strip Packing问题。思路为:首先依次调用AiBi算法族按照跳跃式查找的方式计算,直到将所有矩形块放入矩形容器为止,然后用折半查找的方式进一步缩小矩形容器的宽度,其中1≤i≤12。 具体计算步骤用伪C语言表示如下。 Step2调用AiBi算法族作跳跃式查找: for(l=LB; ;l+=d){ finish_flag=0; 将矩形容器的宽度设定为l; /*循环,依次调用算法族中的12个算法*/ for(i=1;i<=12;i++){ /*循环,依次选取不同的N值*/ for(N=5;N<=205;N+=100){ 调用AiBi算法计算; 若矩形块已全部放入矩形容器,则UB=l,finish_flag=1,break;} if(finish_flag==1) break;} if(finish_flag==1) break;} if(UB==LB) 转Step 4; else 转Step 3; Step3调用AiBi算法族作折半查找: head=UB-d+1;tail=UB-1; while(head<=tail){ finish_flag=0; mid=(head+tail)/2; 将矩形容器的宽度设定为mid; for(i=1;i<=12;i++){ for(N=5;N<=205;N+=100){ 调用AiBi算法计算; 若矩形块已全部放入矩形容器,则UB=mid,finish_flag=1,break;} if(finish_flag==1) break;} if(finish_flag==1)tail=mid-1; elsehead=mid+1; } Step4输出UB值以及对应的布局。 对上述算法步骤补充说明:N值是优美度枚举子程序的重要参数。N值较小时,计算时间较少,但可能漏掉好的占角动作;N值较大时,花时间较多,可能发现更好的布局。本文设定N值从5开始,每次递增100,到205为止。 本文提出的拟人型全局优化算法族AiBi用C语言实现,在CPU为3.0 GHz的个人电脑上做了测试。计算结果如表1~表5所示所示。 Table 1 Comparison of the computational results on the instances (OF) AiBi与当前文献中几种较先进的算法做了比较。除了QH(Quasi-Human )算法[25]是一种非随机型算法以外,GRASP(Greedy Randomized Adaptive Search Procedure)[11]、ISA(Intelligent Search Algorithm)[12]、IDBS(Iterative Doubling Binary Search)[13]、SRA(Simple Randomized Algorithm )[14]、HA(Hybrid Algorithm )[16]和AiBi算法均为随机型算法。对每个问题实例,非随机型算法只需计算一次,随机型算法计算10次。 表1~表5中的符号含义列举如下:对于一个问题实例(Instance)来说,n表示矩形块数,W表示矩形容器的长度(固定值),H*表示矩形容器的宽度的最小值或最小值的下界,H表示非随机型算法所算出的矩形容器宽度,T表示计算时间,单位为s。对于随机型算法来说,AH和BH分别表示10次计算所得到的矩形容器宽度的算术平均值和最小值。AT则表示10次计算时间的算术平均值。 表1给出了算法计算6组共165个benchmark实例的平均相对误差,AiBi的平均相对误差为1.05,在参加比较的7个算法中最小。 表2给出了算法计算C组实例的结果。AiBi的计算时间略长于QH算法,但所生成解的质量较高。除了C19和C21两个实例以外,对本组其它19个实例均能算出最优解。 表3给出了算法计算N组实例的结果。AiBi算法生成了全部实例的最优解。 表4给出了算法计算CX组实例的结果。AiBi算法所生成布局的优度与QH算法相当。 表5给出了算法计算ZDF组实例的结果。除zdf6和zdf7以外,对本组其它19个实例均能算出最优解。算法对zdf6和zdf7所生成的布局刷新了当前文献中已报道的记录。 Table 2 Computational results on the instances C (OF) Table 3 Computational results on the instances N(OF) Table 4 Computational results on the instances CX(OF) Table 5 Computational results on the instances ZDF(OF) GRASP、ISA、IDBS、SRA、HA算法的每次计算的时间上限均为60 s。 AiBi算法计算所需时间总体上较长,生成布局的质量较高。在对布局质量要求高且计算时间限制较宽松的应用场景有其实用价值。 以占角式基本算法为基础,本文提出了一种三阶段拟人型全局优化算法,由邻域搜索、跳坑策略、优美度枚举组成。对benchmark问题实例的测试结果表明,算法生成布局的优度较高。 [1] Huang Wen-qi,Chen Duan-bing,Xu Ru-chu.A new heuristic algorithm for rectangle packing [J].Computers & Operations Research,2007,34(11):3270-3280. [2] He Kun,Ji Peng-li,Li Chu-min.Dynamic reduction heuristics for the rectangle packing area minimization problem [J].European Journal of Operational Research,2015,241(3):674-685. [3] Alvarez-Valdes R, Parreno F, Tammrit J M.A branch and bound algorithm for the strip packing problem [J].OR Spectrum,2009,31(2):431-459. [4] Jiang Xing-bo, Lü Xiao-qing,Liu Cheng-cheng.Lowest-level left align best-fit algorithm for the 2D rectangular strip packing problem[J].Journal of Software,2009,20(6):1528-1538.(in Chinese) [5] Cui Yao-dong, Yang Yu-li, Cheng Xian,et al.A recursive branch-and-bound algorithm for the rectangular guillotine strip packing problem[J].Computers & Operations Research,2008,35(4):1281-1291. [6] He Kun, Huang Wen-qi,Jin Yan.Efficient algorithm based on action space for solving the 2D rectangular packing problem[J].Journal of Software,2012,23(5):1037-1044.(in Chinese) [7] Wang Lei, Yin Ai-hua. A beauty degree enumeration algorithm for the 2D rectangular packing problem[J].Scientia Sinica Informationis,2015,45(9):1127-1140.(in Chinese) [8] Huang Wen-qi,Chen Duan-bing.An efficient heuristic algorithm for rectangle-packing problem[J].Simulation Modelling and Practice Theory,2007,15(10):1356-1365. [9] He Kun,Huang Wen-qi.An efficient place heuristic for three-dimensional rectangular packing[J].Computers & Operations Research,2011,38(1):227-233. [10] Huang Wen-qi,He Kun.A pure quasi-human algorithm for solving the cuboid packing problem[J].Science in China Series F:Information Sciences,2009,52(1):52-58. [11] Alvarez-Valdes R, Parreno F,Tammrit J M.Reactive GRASP for the strip-packing problem[J].Computers & Operations Research,2008,35(4):1065-1083. [12] Leung S C H, Zhang De-fu.A two-stage intelligent search algorithm for the two-dimensional strip packing problem[J].European Journal of Operational Research,2011,215(1):57-69. [13] Wei Li-jun,Oon Wee-chong, Zhu Wen-bin, et al. A skyline heuristic for the 2D rectangular packing and strip packing problems[J].European Journal of Operational Research,2011,215(2):337-346. [14] Yang Shuang-yuan, Han Shui-hua, Ye Wei-guo.A simple randomized algorithm for two-dimensional strip packing[J].Computers & Operations Research,2013,40(1):1-8. [15] Wei Li-jun, Qin Hu, Cheang B, et al.An efficient intelligent search algorithm for the two-dimensional rectangular strip packing problem[J].International Transactions in Operational Research,2016,232(1-2):65-92. [16] Zhang De-fu,Che Yu-xin,Ye Fu-rong,et al.A hybrid algorithm based on variable neighborhood for the strip packing problem[J].Journal of Combinatorial Optimization,2016,32(2):513-530. [17] He Kun,Huang Wen-qi,Jin Yan.An efficient deterministic heuristic for two-dimensional rectangular packing[J].Computers & Operations Research,2012,39(7):1355-1363. [18] Hopper E,Turton B.An empirical investigation of metaheuristic and heuristic algorithms for a 2D packing problem[J].European Journal of Operational Research,2001,128(1):34-57. [19] Burke E,Kendall G,Whitwell G.A new placement heuristic for the orthogonal stock-cutting problem[J].Operations Research,2004,52(4):655-671. [20] Ferreira E P, Oliveira J F.Algorithm based on graphs for the non-guillotinable two-dimensional packing problem[C]∥Proc of the 2nd ESICUP Meeting,2005:131-135. [21] Christofides N, Whitlock C.An algorithm for two-dimensional cutting problem[J].Operations Research,1977,25(1):30-44. [22] Beasley J. An exact two-dimensional non-guillotine cutting tree search procedure[J].Operations Research,1985,33(1):49-64. [23] Bengtsson B E.Packing rectangular pieces-a heuristic approach[J].Computer Journal,1982,25(3):253-257. [24] Riff M C,Bonnaire X,Neveu B.A revision of recent approaches for two-dimensional strip-packing problems[J].Engineering Applications of Artificial Intelligence,2009,22(4-5):823-827. [25] Wang Lei,Yin Ai-hua.A quasi-human algorithm for the two dimensional rectangular strip packing problem:in memory of Prof.Wenqi Huang[J].Journal of Combinatorial Optimization,2016,32(2):416-444. 附中文参考文献: [4] 蒋兴波,吕肖庆,刘成城.二维矩形条带装箱问题的底部左齐择优匹配算法[J].软件学报,2009,20(6):1528-1538. [6] 何琨,黄文奇,金燕.基于动作空间求解二维矩形Packing问题的高效算法[J].软件学报,2012,23(5):1037-1044. [7] 王磊,尹爱华.求解二维矩形Packing问题的一种优美度枚举算法[J].中国科学(信息科学),2015,45(9):1127-1140.2 拟人算法策略
2.1 基本定义

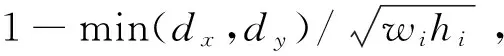

2.2 基本算法
2.3 拟人型全局优化算法(A1B1)整体框架
2.4 初始点的生成
2.5 邻域搜索子程序
2.6 跳坑策略子程序
2.7 优美度枚举子程序
2.8 拟人型全局优化算法族
3 算法优度的理论分析
4 实验结果与分析
4.1 二维矩形Strip Packing问题
4.2 拟人型全局优化算法族求解Strip Packing问题

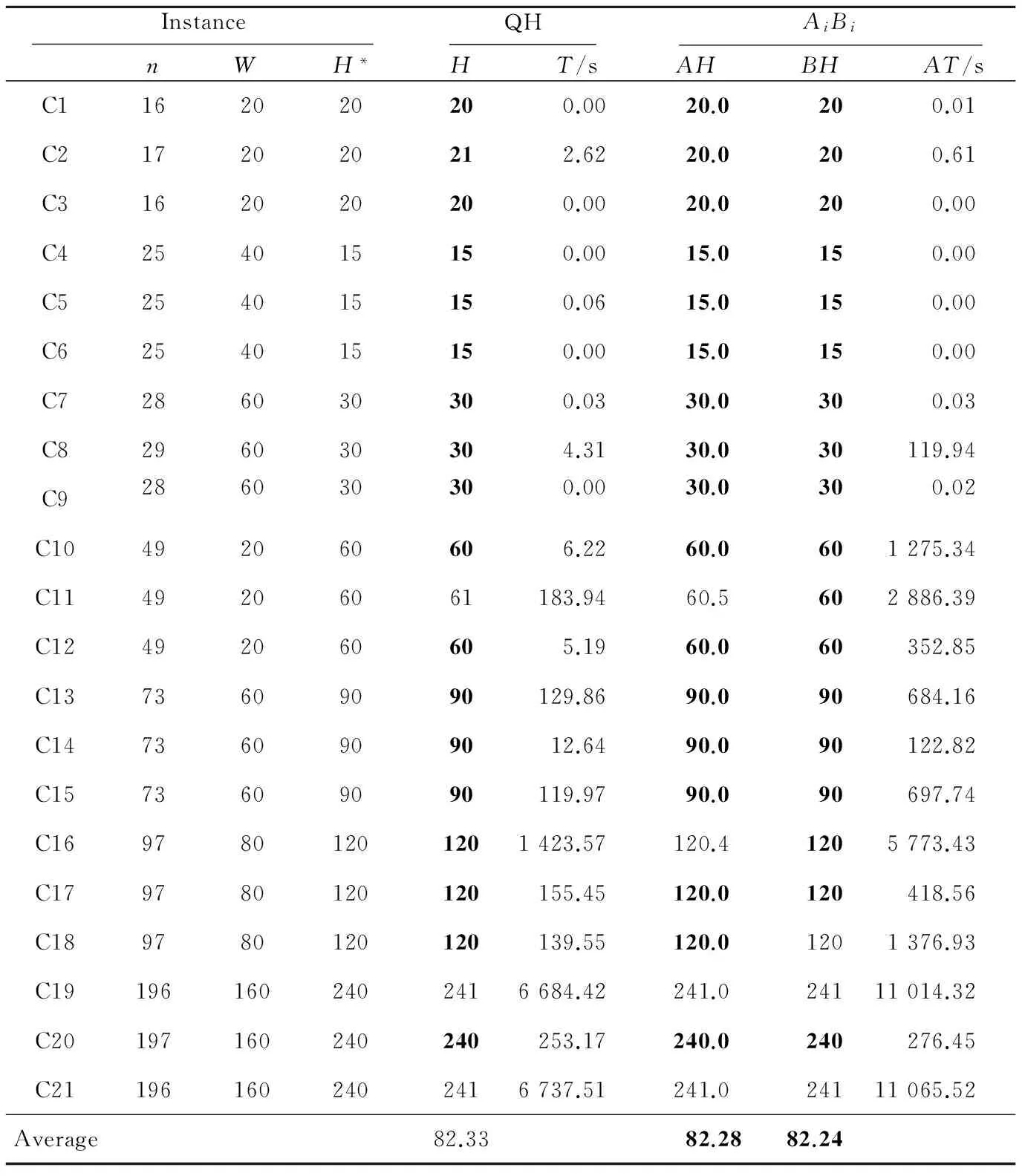
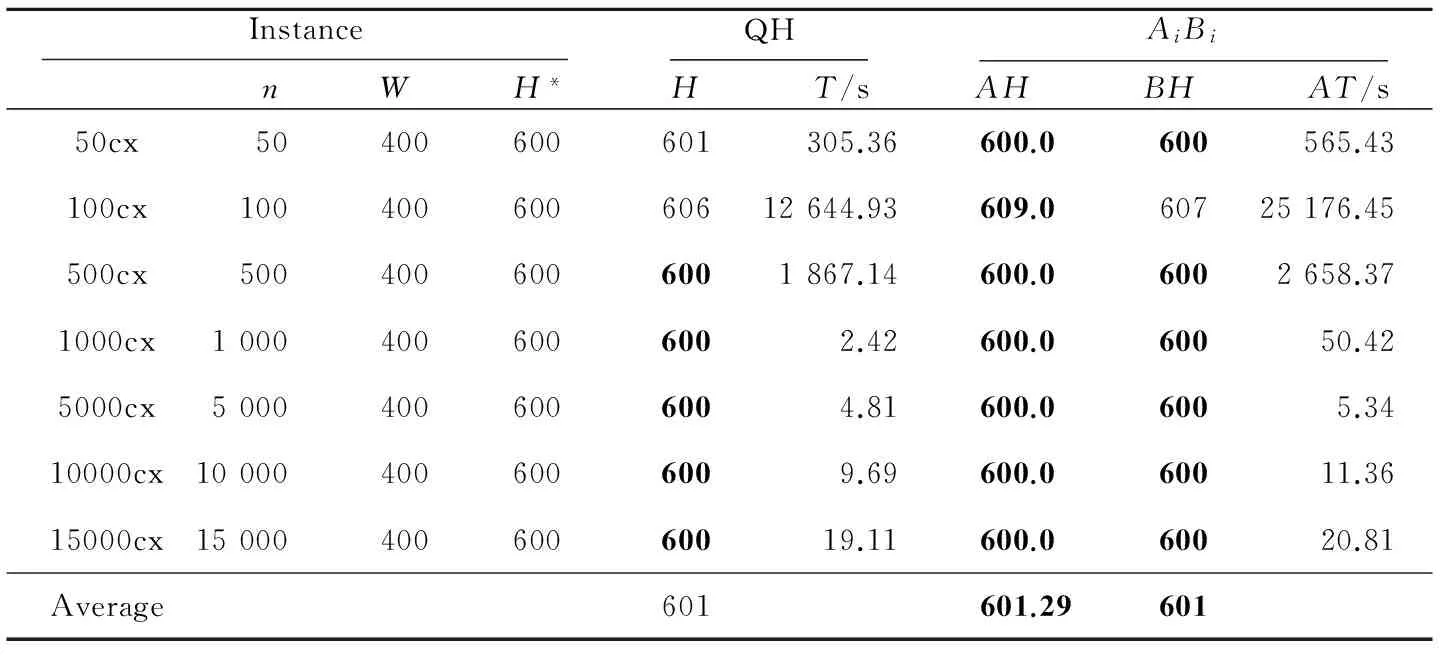
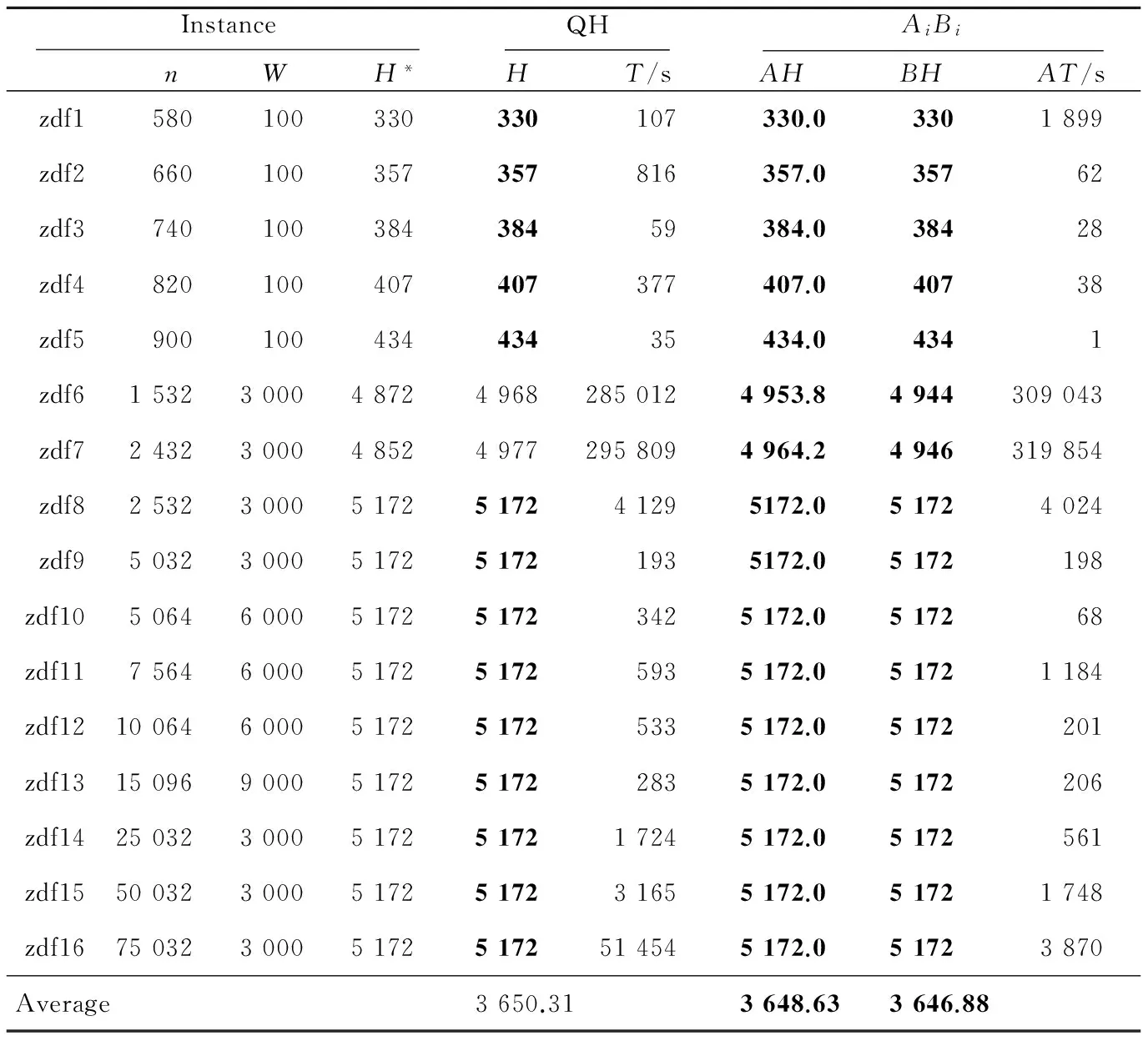
4.3 算法计算结果


5 结束语
