基于聚类分析优化的距离修正室内定位算法

杜佳星,陈亚伟,张 静

(天津大学电子信息工程学院,天津 300072 )

1 引言

室内定位是指采用无线通讯、基站定位、惯性导航定位等多种技术，在室内环境中实现位置定位，从而实现对室内人员、物体等的位置监控。人们的日常生活和工作大多处于室内，随着移动互联网和智能设备的快速发展，室内定位技术成为O2O、智能家居、室内机器人等应用的瓶颈，基于室内定位技术的应用有着迫切的需求和广泛的应用前景。

目前主流的室内定位技术可以分为两大类：基于非测距和测距的定位算法[1]。前者主要是通过节点间的连通性和多条路由来对距离进行估算，对硬件要求比较高，主要有质心算法[2]、DV-Hop算法[3]、近似三边内角测试算法APIT(Approximation Point-In-Triangulation Test)[4]等；基于测距的算法主要是通过测量相邻传感器节点的距离、方位角度等信息，使用三边测量、三角测量、最大似然估计等定位算法建立数学模型，估算出节点位置，从而获得未知节点的实际位置信息。基于非测距的定位算法只是停留在理论研究阶段，且大都是在仿真环境下进行的，需要假设很多不确定因素，而这些因素在实际应用中往往不能满足，因此在实际应用中通常采用测距算法。常采用的测距技术包括RSSI(Received Signal Strength Indicator)[5]、AOA(Angle Of Arrival)[6]、TOA(Time Of Arrival)[7]和TDOA(Time Difference On Arrival)[7]等。其中，基于RSSI测距定位算法具有成本低、功耗低且复杂度低的优势，被广泛采用。

在实际应用中，由于受多径衰减、环境噪音、信号传输的反射、绕射、衍射现象以及天线增益等问题的影响，传统的RSSI测距方法存在较大缺陷，且算法对于测距精度的容错能力有限，若后续定位算法基于该测距方法，最终定位结果必然导致较大误差。并且，现有的定位算法大部分在Matlab、NS2等仿真软件下完成性能测试，极少在实际环境中实现，不能完全体现定位算法[8]，尤其是基于RSSI方案在复杂的室内环境下的真实性。

针对以上问题，本文提出了一种基于聚类算法分析的高斯混合滤波的蓝牙4.0 RSSI信号处理优化策略和优化权值及距离修正的四边质心定位算法，从测距和定位两方面对传统的RSSI定位算法进行优化处理，从而有效提高了室内定位精度，并在实际环境中进行了应用。

2 基于聚类算法分析高斯混合滤波的RSSI优化策略

2.1 无线信号传输模型

RSSI测距原理是，无线信号随距离的增加传播信号强度也随之发生衰减，根据无线信号传输中普遍采用的理论模型——Shadowing 模型，其具有对数衰减特性，公式如下：

(1)

其中，d0为参考距离(一般为1 m)；RSSI0是距离为d0时接收到的信号强度；d是实际距离；RSSI为距离为d时接收到的信号强度；n为与环境密切相关的无线信号衰减因子；ε为一个均值为零的高斯随机变量。

在无线信号传输的实际过程中，很容易受到环境因素的干扰，比如多径、绕射、障碍物、温湿度变化等因素的影响。为了使RSSI测距模型尽可能真实地反映室内实验环境的传播特性，本文采用最小二乘法对不同距离下的信号强度RSSI值，进行二次回归拟合得到最适应该环境的对数路径损耗模型公式，提高实验环境中的测距精度。

2.2 RSSI信号处理优化策略

利用RSSI测距时，由于室内环境中干扰的存在以及多径效应、非视距等影响，同一信标同一距离处的RSSI值往往会出现较大波动，如图1所示，这些异常值会干扰定位精度[9]。本文设计了基于聚类算法分析的高斯混合滤波的RSSI信号处理优化策略，滤除因多径效应、非视距等产生的噪声，排除信号散射、多路径等因素给实验结果带来的误差，以提高测距精度，增强定位信息的准确性。

Figure 1 Distribution of RSSI samples 图1 RSSI采样值分布情况

高斯混合滤波优化策略是对同一蓝牙信标节点在同一距离处采样RSSI值，利用聚类算法中的最大期望算法M-Step(Maximization Step)对采样数据进行聚类分布，即使用高斯混合滤波模型GMM(Gaussian Mixture Model)分析采样数据，将采样数据分解为若干高斯概率密度函数的模型，之后通过赤池信息量准则AIC(Akaike Information Criterion)选择适合RSSI采样数据分布情况的分簇方式优化采样值，并对优化的采样值进行均值计算。

根据实际测试的经验，高斯混合滤波模型选取最多包含三种高斯概率密度函数的模型，即采样值分布滤波模型包含三种情况：一个Component、两个Component和三个Component。在实际实验中采样值分布多于三个Component的情况属于小概率事件，且该情况使用三个Component模型处理的效果理想。

(1)一个Component的高斯混合滤波模型。

高斯模型的分布密度函数：

(2)

其中，

(3)

(4)

根据实际测试的经验，选取经验值RSSI∈[0.15σ+μ,μ+3.09σ]的数据值，并对该范围中的RSSI值求均值作为优化后精确的RSSI值。

(2)两个Component的高斯混合滤波模型。

对于使用多个Component的高斯混合滤波模型，依据聚类算法中的最大期望EM(Expectation Maximization)算法对获取到的RSSI数据进行聚类分簇，即使用EM算法中的E-Step(Expectation Step)和M-Step(Maximization Step)，对每个RSSI采样值计算后验概率和相对应的概率密度函数，并根据后验概率对数据进行重新估计聚类分布，不断重复迭代两种算法，使得聚类数据的似然性最大。

①E-Step算法。

E-Step算法的作用是计算数据的后验概率，即分别求出每个RSSIi属于每个Component的后验概率。

使用两个Component的E-step聚类算法如下：

RSSIi属于Component1的概率：

γ1(RSSIi)=

(5)

RSSIi属于Component2的概率：

γ2(RSSIi)=

(6)

RSSIi属于哪个Component的概率最高，再次遍历时将会被分配在这个Component中。

②M-Step算法。

M-Step算法的作用是重新估计分布参数，以使得数据的似然性最大。其主要用来计算不同Component相对应的均值μ、方差σ2以及概率密度函数f(RSSIi;μ,σ2)。

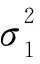
(3)三个Component的高斯混合滤波模型。

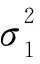
(4)高斯混合滤波模型的AIC选取评估。

对采集到的RSSI采样值利用聚类算法，分别使用一个Component、两个Component和三个Component的高斯混合滤波模型进行处理后，利用赤池最小信息准则AIC进行滤波模型的选取。AIC准则可以权衡所估计模型的复杂度和此模型拟合数据的优良性，是信号处理中对多种模型作选择的判别方法。

AIC表示为：

AIC=2k-2ln(L)

(7)

其中，k是参数的数量，L是似然函数。

赤池信息准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型，即优先考虑的模型应是AIC值最小的那一个。

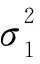
(8)

(9)

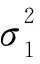
(10)

(11)

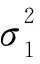
(12)

(13)

分别计算三种分布的AIC值，取AIC值最小的那个分布作为RSSI采样值筛选优化机制的滤波分布，并求该Component的均值，作为优化校正的RSSI值代入无线信号对数衰减模型公式(1)中进行RSSI-距离转换。

3 基于优化权值及距离修正的四边加权质心定位算法

基于无线信号传播模型即可利用RSSI值求得蓝牙信标节点到移动终端间的距离，当移动终端获取到了至少三个蓝牙信标节点的距离值后，就可以采用质心定位算法进行位置估算，获得移动终端位置信息。本文对传统质心算法、加权质心算法进行分析，优化权值因子，并在此基础上对定位算法进行距离修正，提高了定位算法在实际应用中的适应性和精确度。

3.1 传统质心定位算法

质心算法[10]是一种与距离无关、基于连接性的简单算法，根据节点接收到的信号强度和连通性进行定位。假设三个信标节点坐标为：(xA,yA)，(xB,yB)，(xC,yC)，则传统质心算法未知节点坐标为：

(14)

这种质心算法所需的设备简单，易于实现，受环境的影响小。但是，这种算法忽略了信标节点对未知移动终端的影响，即当每个信标节点接收到的RSSI值不同时，信标节点坐标对未知节点的决定权大小也不相同。

3.2 加权质心定位算法

针对传统质心算法的缺陷，文献[11]提出了一种加权质心算法。加权质心算法通过RSSI值来计算每个信标节点对未知节点贡献的权值。具体算法是：由于RSSI值易受环境干扰以及电磁场信号无规律衰减等因素的影响，转化成距离时必然存在误差，因此信标节点的感知交集不是一个点，而是一个区域，未知节点就在该区域内。如图2所示，已知三个信标节点分别为：O1(x1,y1)、O2(x2,y2)、O3(x3,y3)，D点为未知节点，D点到三个信标节点的测距距离为r1、r2、r3。根据未知节点到信标节点的距离与坐标的数学模型：

Figure 2 Trilateral location algorithm图2 三边定位算法

(15)

两两圆求交点，得到交点A(xA,yA)、B(xB,yB)、C(xC,yC)，未知节点就在三角形ABC区域内。加权质心算法在每次定位估计中引入一个权值来防止信息淹没现象(即信标节点的相关信息对质心坐标估算的影响因素)。该权值与距离相关，利用距离因子来体现信标节点对未知节点未知的影响程度(即信标节点与未知节点越远，位置估计时所占比重越小)，而每个顶点由两个距离确定，故权值选择为1/(r2+r3)(以圆O1为例，r2、r3为圆O2、O3半径)，由此得到未知节点坐标为：

(16)

3.3 优化权值的加权质心算法

加权质心算法利用RSSI相关数据信息，提高了定位算法的精度，但该权值的选择存在很大的不合理性，假设ra>rb，即rb距离未知节点距离较近，对其未知节点的作用效果大；但若采用1/(ra+rb)为权值，使ra起了主导作用，rb对未知节点的作用效果减弱，这与加权质心定位算法的意图相违背。

文献[12]指出RSSI测距与误差存在如下关系：

φ(x)=εx+δ

(17)

其中，ε是一次误差系数，δ是常误差系数。

由此可见误差与距离存在一定的线性关系，经过转化得到：

φ(x)-δ=εx

(18)

(19)

本文对权值因子进行如下优化：

(20)

其中，da、db分别为未知节点到信标节点的距离。

如此优化后，da、db就可根据自身距离大小对未知节点进行相应权值的贡献，符合加权质心定位原理的理论。优化后加权质心算法的未知节点坐标如式(21)所示：

(21)

使用上述三种定位算法，于6 m*8 m的会议室中，使用三个蓝牙信标节点围成等腰三角形区域，节点坐标分别为(0,2.5)、(5,5)和(5,0)，将移动终端放置在该区域内10个不同位置进行定位实验，得到三种定位算法对应的定位平均误差，如图3所示。

Figure 3 Average error of different localization algorithms图3 定位算法平均误差图

加权质心算法同传统质心算法相比并没有明显的定位精度的提升，平均误差仅仅提高了0.256 m，而采用优化权值的质心算法的定位精度提高了0.825 m，远高于其他算法，较大提高了定位系统的精度。

3.4 基于距离修正的室内定位算法

由于多径衰减、障碍物等噪声的干扰，信号强度值往往会出现较大的波动，使得RSSI值转换出的距离值误差较大，导致基于RSSI测距方法得到的未知节点到信标节点的距离远远偏差于实际距离，以致三个圆无法满足两两相交，加权质心定位算法失效。本文针对这一问题提出了一种基于距离修正的加权质心定位算法，在圆与圆之间不相交的情况下能够准确进行节点定位，提高在室内环境中定位算法的容错能力、适应性及精确度。

圆与圆之间存在两种位置关系会导致定位算法失效：两圆相离以及两圆内含。

(1)两圆相离。

当圆与圆之间存在两圆相离的情况时，即两圆无交点，如图4所示。本文使用的RSSI距离修正原理是:以距离因子作为权值分别增大两圆的半径，使圆与圆两两相交，形成一个重叠的区域，且使用该方法可保证增大后的半径比与之前半径比保持不变，即距离因子对未知节点所占权重不变。再使用加权质心三边定位算法求得未知节点坐标。

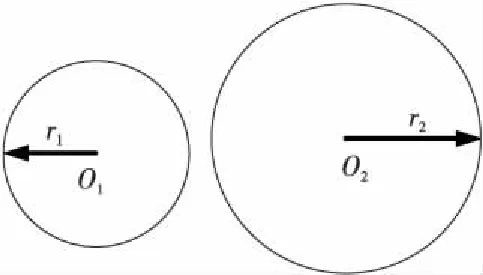
Figure 4 Separation of two circles图4 两圆相离

半径增大方案如式(22)所示：

(22)

其中，r1、r2为两圆O1、O2半径，d为两圆圆心距离。

(2)两圆内含。

当两圆之间呈现内含的情况时，如图5所示。本文通过减小半径较大的圆的半径使之与半径较小的圆相切或相交来纠正RSSI距离，使圆与圆获得公共交点。具体修正方案如式(23)所示：

(23)

Figure 5 Inclusion of two circles图5 两圆内含

其中，r1、r2分别为圆O1、O2的半径，且r1>r2，d为两圆圆心距离。使用该方法可以在尽量减小两圆偏移量的基础上保证两圆半径比变化尽可能小。

传统的加权质心三边定位算法是使用三个信标节点进行定位，得到的定位结果有较大误差，为了进一步提高未知节点的定位精度，通过理论与实际应用分析，本文提出四边测距定位算法，即在三边定位算法基础上增加一个信标节点进行定位。

设增加未知节点为O4(x4,y4)，根据圆的参数方程几何关系，三三自由组合，求得交点坐标，可分别得出，通过O1O2O3三圆得到估计位置A(xA,yA)，通过O1O2O4三圆得到估计位置B(xB,yB),通过O1O3O4三圆得到估计位置C(xC,yC)，O2O3O4三圆得到估计位置D(xD,yD)，对ABCD四组估计位置求质心得到更加精确的未知节点坐标O(x,y)，如式(24)所示：

(24)

3.5 基于信号强度优化的距离修正室内定位算法伪代码

根据以上提出的优化距离修正策略的四边加权质心定位算法伪代码如下：

AlgorithmIndoorPosition()

{

/*获取当前侦测到周围的四个蓝牙信标节点发送的UUID、RSSI、POWER信息*/

info[infoIndex].UUID,Power,Rssi;

If (同一UUID获取到的Rssi值数目大于100)

{

/*对100个RSSI值进行聚类分析的高斯混合滤波算法进行筛选，得到优化的RSSI值*/

对100个RSSI值分别使用包含一个Component、两个Component和三个Component的高斯混合滤波模型中，使用聚类算法进行分簇处理，并求出相应收敛参数。使用AIC准则对三种滤波模型进行评估，选择最优滤波模型，求滤波后RSSI均值。

/*利用对数路径损耗模型将RSSI值转换成距离d*/

d=distanceRSSI(Power,Rssi);}

Else {/*继续获取蓝牙信标节点信息*/}

/*依次求两个蓝牙信标节点为圆心的圆的交点*/

If (两圆无交点)

{ /*使用距离修正方案修改半径距离*/

revise(circles[].center.x,circles[].center.y,circles[].r)；}

Else(两圆存在交点)

{/*根据圆的几何关系，求两圆交点*/

insect(circles[0].center.x,circles[0].center.y,circles[0].r,circles[1].center.x,circles[1].center.y,circles[1].r)

}

/*利用求得的交点，进行四边加权质心定位算法运算*/

computer(info[infoIndex].UUID,Power,Rssi,d)；

}//END

4 定位实验及结果分析

本系统由四个蓝牙信标节点和一个移动智能终端树莓派组成。其中蓝牙信标节点核心控制器为TI公司的CC2540蓝牙芯片，该芯片使用了最新的蓝牙4.0技术，具有功耗小、时延低、传输距离远的特点，最大限度地满足了高精度室内定位技术的要求。移动终端树莓派是一款基于ARM的微型电脑主板，其支持Linux系统。移动终端树莓派通过蓝牙模块接收到蓝牙信标节点发送的与位置相关的UUID、RSSI值和POWER值(距离终端1 m处的RSSI值)，通过加权质心定位算法即可定位未知节点坐标。基于蓝牙信标节点和树莓派的定位实验原理如图6所示

Figure 6 Localization experiment principle based on bluetooth beacon nodes and Raspberry图6 基于蓝牙信标节点和树莓派的定位实验原理图

4.1 建立无线信号传输模型

本实验选择了一个6 m*8 m的会议室作为实验场地，该会议室为真实工作环境，其中内置桌椅，该环境中的内置物皆会对无线信号产生多径效应等影响。首先进行测距实验：固定树莓派在房间中，然后分别在距离该树莓派0.5 m、1 m、…、8 m处设置蓝牙信标节点，共有16个测试点。在每个测试点上，通过树莓派进行RSSI值采样，蓝牙信标节点每0.1 s广播一次，测试中每个测试点采样20 s，获取到200个RSSI样本点。然后对采集到的数据进行高斯滤波和均值滤波处理，剔除RSSI波动较大的值，最终获得较为准确的RSSI值。对16个测试点进行测量后，得到的适应该实验环境的无线信号传输模型如图7所示。

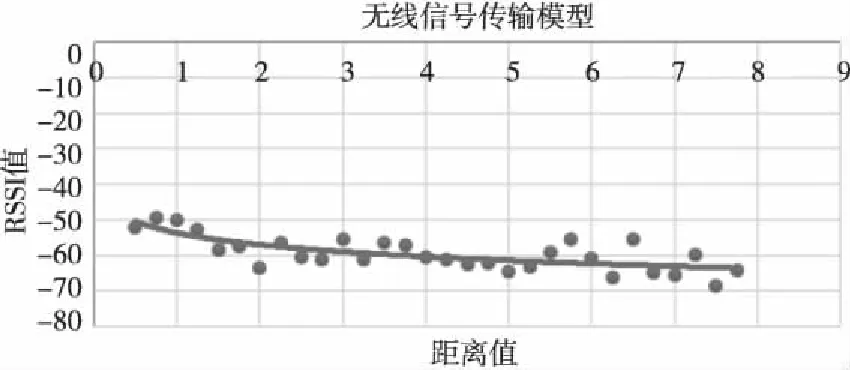
Figure 7 RSSI-distance logarithmic fitting formula图7 RSSI-距离对数拟合公式

对该测试曲线使用RSSI=RSSI0+10nlg(d/d0)+ε对数模型进行拟合，最终得到该曲线拟合函数如式(25)所示。

RSSI=-6.661ln(d)+power+8.711

(25)

4.2 RSSI信号处理优化实验及分析

本文的测试程序是基于Linux下的bluz协议栈，使用智能终端树莓派、蓝牙信标节点以及一套C开发的上位机程序作为开发平台，选择了一个3 m*7 m的空旷走廊作为实验场地，实验布局如图8所示。其中AB侧为墙壁(内部为金属结构，易造成多径效应)、CD侧为空旷视野。将四个蓝牙信标节点分别置于实验区域的(0,0)、(7,0)、(7,3)、(0,3)坐标位置，使用移动终端树莓派进行RSSI采样、滤波处理，得到优化的RSSI值，根据4.1节中拟合出的适应该环境的对数距离损耗模型，计算出RSSI对应的距离值。

Figure 8 Optimization of RSSI experiment layout图8 RSSI值优化实验布局

移动终端树莓派依次经过3个指定位置进行测距实验，RSSI信号处理优化策略分别使用传统高斯滤波及本文提出的基于聚类算法分析的高斯混合滤波模型两种方式，分别处理四个信标节点A、B、C、D到树莓派位置1、2、3的RSSI值，本实验中树莓派每个位置采集来自每个信标节点的10组RSSI值，每组100个采样值进行滤波计算。将使用不同滤波方法优化的RSSI代入到式(26)中，得到其对应的距离值测距误差公式为：

△d=|d-dt|

(26)

其中，d为测量距离，dt为真实距离。

两种滤波方法实验结果的平均测距误差分析如表1和表2所示。

Table 1 Average distance error of point A、D to the positon 1、2、3

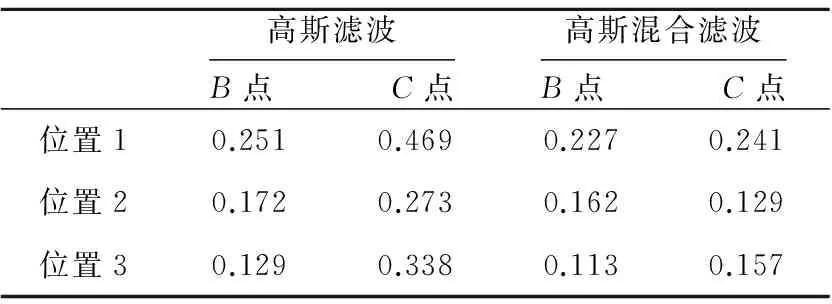
Table 2 Average distance error of point B、C to the positon 1、2、3

由表1和表2可知，基于聚类算法分析的高斯混合滤波优化机制明显优于传统高斯滤波方法，其平均测距误差为0.162 m，测距精度较传统高斯滤波方法提高了52.02%，并且可看出，CD边为空旷地带，无障碍物干扰，信标节点A、B广播的信号比较纯净、无杂波，因此A、B信标节点使用两种滤波方式的精度相差不大；而AB边为墙壁，信标节点C、D广播的信号出现多径效应、散射等干扰，移动端获取到的RSSI分布比较复杂。而由表2 可以看出，使用本文提出的高斯混合滤波方法有效滤除了因复杂室内环境所导致RSSI异常值，测距精度大大提高，提高了室内定位的适应性。

4.3 定位算法实验及结果分析

关于定位的实验测试，选择了一个6 m*8 m的会议室作为实验场地，该会议室为真实工作环境，其中内置桌椅，该环境中的内置物皆会对无线信号产生多径效应等影响。实验现场如图9所示。将四个蓝牙信标节点分别置于房间的(0,0)、(0,6)、(0,6)、(6,6)坐标位置，使用移动终端树莓派进行对RSSI采样、滤波处理，拟合出适应该环境的对数距离损耗模型，之后通过基于距离修正策略的四边测距定位算法得出移动终端树莓派的坐标位置。

Figure 9 Experimental site layout图9 实验现场布局

移动终端树莓派依次经过5个指定位置进行定位测试，分别使用加权质心算法及本文提出的基于距离修正的加权质心定位算法两种方式，每5 s反馈一次定位信息，在每个测试点记录10次定位点的坐标，每次然后计算定位的相对精度，即定位误差。定位误差公式为：

(27)

其中，(x，y)为移动终端树莓派定位得到的位置信息，(xe，ye)为真实位置。两种定位算法实验结果的定位误差最大值、最小值和平均值如表3所示。

Table 3 Experimental results of the two localization algorithms

由此得到加权质心算法和修正距离的加权质心算法的平均误差如图10所示。由图10可以得出，在相同测试环境下，优化方法的平均定位误差明显小于原始定位方法产生的误差，测试中，使用加权质心算法的平均定位误差约为0.750 m，而采用本文提出的距离修正的加权质心定位算法的平均定位误差仅为0.483 m，性能提高约35.6%。

Figure 10 Average error comparison chart图10 平均误差对比图

5 结束语

针对室内复杂的环境使无线信号出现多径效应的现象，本文提出了基于聚类分析优化的距离修正室内定位算法，使用基于聚类分析的高斯混合模型的优化策略，提高了测距精度。并且在传统定位算法基础上考虑因RSSI测距误差导致三边定位算法失效的情况，利用距离修正方案，提高定位的相对精度，即减小了定位误差。实验结果表明，利用聚类分析的高斯混合滤波RSSI筛选策略可以减小室内复杂环境影响和多径效应干扰对RSSI测距带来的误差，以及使用距离修正的加权四边质心定位算法相对于传统方法获得了更高定位精度以及更好的容错能力(即加权质心定位算法失效情况)，可以更好地应用于室内定位。但是，本文提出的定位算法仍无法实现智能终端在移动状态下实时定位，该机制将作为后续研究发展的主要方向。

[1] Dang Xiao-chao, Li Xiao-yan.Weighted correction model in wireless sensor network localization [J].Journal of Computer Applications,2012,32(2):355-358.(in Chinese)

[2] Pawel K,Javier A,Esteban E,et al.Angle-of-arrival localization based on antenna arrays for wireless sensor networks [J].Computers and Electrical Engineering,2010,36(6):1181-1186.

[3] Kumar S,Lobiyal D K.An advanced DV-hop localization algorithm for wireless sensor networks [J].Wireless Personal Communications,2013,71(2):1365-1385.

[4] Li X F, Chen L F, Wang J P,et al.Fuzzy system and improved APIT (FIAPIT) combined range-free localization method for WSN [J].KSII Transactions on Internet and Information Systems,2015,9(7):2414-2434.

[5] Oliveira L,Li H B,Almeida L,et al.RSSI-based relative localisation for mobile robots [J].AD HOC Networks,2013,13:321-335.

[6] Liu Hsin-chin, Hsuan Cheng-wei. AOA estimation for coexisting UWB signals with multipath channels [C]∥Proc of 2014 International Conference on Telecommunications and Multimedia,2014:173-178.

[7] Le T N,Kim J,Shin Y.TDOA localization based on particle swarm optimization in UWB systems [J].IEICE Transactions on Communications,2011,E94.B(7):2013-2021.

[8] Wang Qian,Jin Guang,Niu Jun.A hybrid localization algorithm based on RSSI [J].Chinese Journal of Sensors and Actuators,2015,12(12): 1823-1829.(in Chinese)

[9] Shi Wei,Gao Jun.An improved weighted centroid localization algorithm based on RSSI for wireless sensor network [J].Computer Appications and Software,2015,12(12): 68-70.(in Chinese)

[10] Ding En-jie, Qiao Xin, Chang Fei,et al.Improvement of weighted centroid localization algorithm for WSNs based on RSSI [J].Transducer and Microsystem Technologies,2013,32(7): 53-56.(in Chinese)

[11] Zhu Xiao-juan, Meng Xiang-rui. An algorithm of mobile node localization based on weighted centroid for wireless sensor networks [J].Computer Engineering & Science,2011,33(11):15-19.(in Chinese)

[12] Peng Bo.RSSI-based range error compensation localization algorithm in WSN [D].Dalian:Dalian University of Technology,2014: 28-30.(in Chinese)

附中文参考文献：

[1] 党小超,李小艳.无线传感器网络节点定位加权校正模型[J].计算机应用,2012,32(2):355-358.

[8] 王千,金光,钮俊.一种基于RSSI的混合定位算法[J].传感技术学报,2015,12(12):1823-1829.

[9] 施伟,高军.无线传感器网络中基于RSSI的改进加权质心定位算法[J].计算机应用与软件,2015,12(12):68-70.

[10] 丁恩杰,乔欣,常飞,等.基于RSSI的WSNs加权质心定位算法的改进[J].传感器与微系统,2013,32(7):53-56.

[11] 朱晓娟,孟祥瑞.基于加权质心的无线传感器网络移动节点定位算法[J].计算机工程与科学,2011,33(11):15-19.

[12] 彭渤.基于RSSI测距误差补偿的无线传感器网络定位算法研究[D].大连：大连理工大学,2014:28-30.