一种顾及加权水平精度因子的室内宽带定位算法

尚俊娜，刘 参

（杭州电子科技大学 通信工程学院，杭州 310018）

全球导航卫星系统（Global Navigation Satellite System,GNSS）有高精度、连续导航等优点，但在室内等复杂环境中，由于障碍物的遮挡使GNSS信号衰减严重[1]，限制了GNSS在室内环境中的应用。人们在高精度室内定位方面开展大量的研究，李楠等[2]提出了一种基于WiFi自适应粒子滤波的室内定位方法，由于WiFi信号带宽较低，无法获得更高的多径分辨能力，使得定位误差较大，不能满足高精度定位需求。尚俊娜等[3]研究的IMU辅助的室内组合定位系统通常基于IMU器件的定位方式采用航位推算算法，该算法具有累积误差效应，使得系统的定位精度较低。隋心等[4]提出基于到达时间差（Time Difference of Arrival,TDOA）的矿井定位技术，在地下矿井等复杂环境下，每个锚节点的测距精度不同，由于未考虑加权水平精度因子（Weighted Horizontal Dilution of Precision,WHDOP）的影响，使得系统定位精度不高。基于锚节点测距的定位系统其定位精度受测距精度和锚节点空间布局等多方面的制约[5-6]。传统定位系统的测距精度与定位信号的带宽B和持续时间Ts（BTs积）有关[7]，带宽越大，系统时间分辨率越高，测距精度越高[8]；HDOP表示系统的定位精度与测距误差的关系，反映了锚节点的空间布局，测距误差相同时，最佳锚节点空间布局对应最小HDOP值，可实现高精度的室内定位。由于定位点与邻近锚节点间很强的空间关联性[3]，使每个锚节点伪距测量精度不同[9]，此时需赋予误差较小锚节点在位置解算过程中具有更大的权重，考虑WHDOP来实现精准定位。

为了提高室内定位系统的精度，并且根据不同锚节点测距的精度分配不同的权重，本文提出了一种基于正弦调频-加权水平精度因子（SFM-WHDOP）的高精度室内定位方法。与常规超宽带-水平精度因子（UWB-HDOP）定位方法进行了对比，仿真得到在室内复杂环境中，SFM-WHDOP方法的定位均方根误差在0.15 m以内，可实现高精度的室内无线定位功能。

1 定位信号伪距的测量精度

伪距的精度与测距信号的模型有关，文献[10]研究了基于 TDOA测距方法伪距的克拉美罗界（Cramér-Rao Low Bound,CRLB）：

其中，c=3×108m/s为光速；B表示信号的带宽（Hz）；Ts表示信号持续时间（s）；SNR（Signal-to-Noise Ratio）表示发射信号dB域的信噪比。

由式(1)可知，伪距精度与信号带宽B和持续时间Ts（BTs积）呈正相关特性，BTs积越大，测距精度就越高，故增加带宽B可提升测距性能。

1.1 宽带调频信号模型

超宽带（UWB）技术以信号带宽大等优点，可满足室内信号对测距精度的要求。常规UWB信号是通过有效信息控制超短脉冲的相对位置，即通过脉冲位置调制（Pulse Position Modulation,PPM）技术实现UWB信号调制。相对于PPM调制方式而言，连续宽带调频信号有：线性调频（Linear Frequency Modulation,LFM）、正弦调频（SFM）、双曲调频（Hyperbolic Frequency Modulated,HFM）、二次调频（Quadratic Frequency Modulation,QFM）等。LFM、SFM、HFM信号广泛应用于雷达、声纳、地震勘测等领域，其中，LFM信号的时域复表达式为

瞬时频率为

SFM信号的时域复表达式为

瞬时频率为

式中，Ts表示脉冲的持续时间；rect（t）为矩形函数；f0表示信号初始频率；β表示 LFM 信号的调频速率，β=（fend-f0）Ts，fend表示LFM信号截止频率；α表示SFM信号带宽；ω表示SFM信号瞬时频率的角频率。

由式(1)可知，定位信号的测距性能与信号的带宽有关，带宽越大，测距精度就越高。为了验证LFM和SFM信号的宽带特性，本文对30 MHz带宽LFM和SFM信号的时域、频域和瞬时频率特性进行仿真，结果如图1所示。由图1可知，两种信号的频谱近似成矩形分布，都有较宽的带宽，可实现高精度的测距性能。

图1 LFM和SFM信号的时域、频域和瞬时频率特性Fig.1 Time domain,frequency domain and instantaneous frequency characteristics of LFM and SFM signals

1.2 测距性能理论分析

宽带模糊函数（Wideband Ambiguity Function,WAF）是分析雷达性能的工具。WAF仅由发射信号决定，反映雷达系统的分辨率、测量精度和目标分辨能力。Kelley-Wishner宽带模糊函数的定义为[11]：

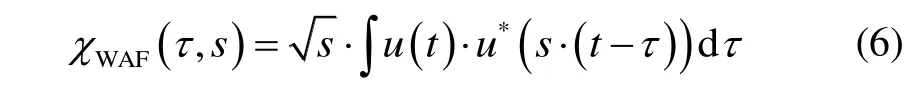
式中，τ是延时因子；s=（c-v）（c+v），v是终端移动的速度，s表示多普勒频移[12]；χWAF（τ,s）可表示信号的距离和速度变化时对目标的分辨特性。根据式(6)定义，锚节点与终端存在相互运动，但运动的速度与光速比起来及其微弱，认为s≅1，此时得到信号的距离模糊函数：

其中，R（τ）是信号的自相关函数，表示s为1时，信号的距离分辨特性。

为了验证不同宽带调频信号的模糊函数性能，本文对常规UWB、LFM和SFM信号的距离模糊函数进行了仿真。仿真参数设置仅有信号模型不一样，其他参数都保持一致。仿真结果如图2所示。

由图2可知，LFM和SFM信号距离模糊函数近似为脉冲状，-3 dB带宽分布更集中，峰值更尖锐，具有更高的距离分辨率。因此理论上认为，LFM和SFM信号的距离分辨率比UWB信号高，测距精度更高。

图2 常规UWB、LFM和SFM信号的距离模糊函数Fig.2 Distance ambiguity function of conventional UWB,LFM and SFM signals

2 改进的WHDOP研究

在导航定位中，常用精度因子（DOP）来评系统性能，系统的定位精度是 DOP与用户等效距离误差（User Equivalent Range Error,UERE）的乘积：

其中，ΔRσ表示定位的位置误差，σUERE表示测距均方根误差，DOP表示测距误差放大系数。DOP分量包括GDOP（几何精度因子）、PDOP（空间精度因子）、HDOP（水平精度因子）、VDOP（高程精度因子）和TDOP（钟差精度因子）。不同系统研究不同的 DOP分量，民航系统对HDOP和VDOP研究更多，授时系统研究TDOP更多。由于室内定位系统认为是水平面内的二维系统，故本文主要研究HDOP。

2.1 水平精度因子（HDOP）

终端坐标R（xu,yu,zu）由锚节点坐标Bi（xi,yi,zi）和伪距ρi决定。基于TDOA的系统中，终端坐标R可通过N个非线性方程组求解：

式中，cΔt表示时钟偏移引起的伪距偏移量；i=1,2,…,N，其中N是锚节点的个数。

其中，

Δρi=ρi-ρi(ρi是锚节点i的伪距估计值)；Δxu=xu-；αxi、αyi、αzi表示R与锚节点i单位矢量间的方向余弦，同样的可得到αyi、αzi的表达式。

令精度因子矩阵G=(HT⋅H)-1，因此 DOP可通过G的主对角线元素定义：

文献[13]研究了HDOP值下界的最小值：

HDOP理论最小值是 1，且随着参与定位锚节点数目的增多，HDOP值单调减小[6]，在不增加系统复杂度与实时性时，可选择最佳锚节点个数实现室内精准定位功能。

2.2 加权水平精度因子

在复杂时变的室内环境中，无线电传播会受到墙壁、桌椅、移动物体或者行人等障碍物的遮挡，发生反射、透射、折射、衍射现象，会出现非视距传播和多径效应[13-15]，使得锚节点的伪距精度与距离等因素有关。文献[10]研究了距离相关噪声模型在实际定位系统中的应用，表明需要根据锚节点测距的精度分配不同的权重[9]，通过加权最小二乘算法求解终端的位置。

矩阵Rρ是观测方程的权重矩阵，则ΔX的加权最小二乘解为[16]：

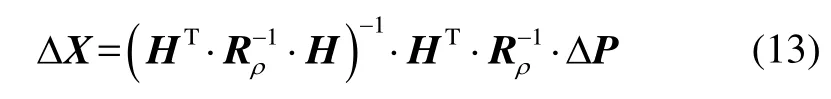
权重矩阵Rρ=diag(σU2ERE,1,σU2E RE,2,,σU2ERE,N)，diag表示对角阵，σU2ERE,i表示第i个锚节点的归一化测距误差。可得到加权精度因子矩阵GW：

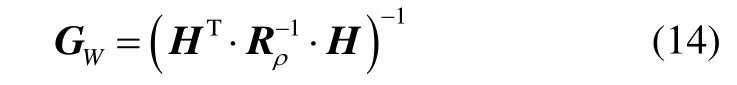
WHDOP可通过GW的主对角线元素定义，

由于考虑到了每个锚节点伪距误差的变化的不确定性，WHDOP能真实地反映定位误差趋势[7]，与常规HDOP相比具有更大的可靠性与鲁棒性。

3 宽带信号定位性能与误差分析

3.1 宽带定位信号测距性能仿真

为了分析不同宽带信号的测距性能，本文对常规UWB、LFM和SFM信号的测距性能在瑞利衰减信道模型中进行仿真，各参数设置如下：发射信号归一化幅度为A=1；带宽B=500 MHz；持续时间Ts=300 ns；信号周期T=500ns；采样频率fs=2.5B；信噪比SNR=-30 dB；距离范围是0～25 m。测距误差如图3所示。表1是不同信号测距性能。

由表1可知，SFM信号的测距性能比LFM和常规UWB信号有所提升；测距均方误差小于0.1 m，精度更高，故此本文采用SFM信号进行定位，可以得到更高精度的室内定位性能。

表1 不同信号的测距性能Tab.1 Ranging performance of the signals

图3 不同信号的测距性能图Fig.3 Ranging performances for different signals

3.2 室内噪声环境下HDOP和WHDOP对测距误差的鲁棒性能分析

不同环境噪声下测距误差不同，为研究HDOP和WHDOP定位方法的鲁棒性能，需对不同环境下定位性能进行仿真，本文采用的噪声环境为高斯噪声环境和瑞利噪声环境。

3.2.1 高斯噪声环境对定位性能影响

本文对测距误差服从期望为 0m，RMS=ε，0≤ε≤2，高斯分布的定位性能进行仿真，其中性能评价用定位均方根误差（RMSE）表示：

其中，ex、ey表示是x、y方向的定位误差分量[15]。

仿真结果如图4(a)所示，由于室内障碍物的遮挡会造成正的测量误差[15]，故本文同时仿真了测距误差的期望为0.5 m时的定位性能，结果如图4(b)所示。

图4 高斯噪声环境中定位误差与测距均方根误差的关系Fig.4 Relationship between location error and ranging RMS error in Gaussian noise environment

由图4(a)知，理想情况下测距误差的均值是0 m，此时在高斯噪声环境中随着测距均方根误差的增大，HDOP和WHDOP的定位性能恶化，但WHDOP方法的定位误差明显优于HDOP方法，对伪距误差的鲁棒性能更强。由图4(b)知，在真实场景中，当测距误差的均值是 0.5 m时，仿真结果得到与图4(a)相同的结论，且当测距均方根误差为2 m时，WHDOP方法的定位误差在1 m左右，而HDOP方法的定位误差超过2 m。由上述结论可知，随着测距误差的增加，WHDOP方法的鲁棒性能更强，可明显改善系统的定位性能。

3.2.2 瑞利噪声环境对定位性能影响

本文对测距误差服从均方根RMS=ϑ,0≤ϑ≤2的瑞利分布的定位性能进行仿真，结果如图5所示。

图5 瑞利噪声环境中定位误差与测距均方根误差的关系Fig.5 Relationship between location error and ranging RMS error in Rayleigh noise environment

图5可知，在瑞利噪声环境中随着测距均方根误差增大，HDOP和WHDOP方法的定位性能恶化，而WHDOP方法性能恶化的速度更慢，故WHDOP方法的定位性能对测距误差的鲁棒性更强。当测距均方根误差是1.3 m时，WHDOP定位误差是1 m，此时HDOP方法的定位误差接近2 m，故此采用WHDOP方式的定位精度更高。

结合图4和图5可知，在不同的噪声环境中，随着室内环境复杂度的增加，HDOP和 WHDOP方法的定位性能恶化，但是不管何种噪声环境，WHDOP定位方法的性能明显优于HDOP方法，同时WHDOP定位方法对不同室内噪声环境具有较强的鲁棒性能。故此，本文采用 WHDOP定位方法的定位性能更优越，定位精度更高。

3.3 常规UWB-HDOP方法与本文采用SFM-WHDOP方法的定位性能仿真

本节对常规UWB和SFM信号进行定位性能仿真。各参数如下：区域是30 m×20 m的二维平面，8个锚节点位置如表2所示，信号模型如1.1节中所示，其中，常规UWB信号采用HDOP定位方法，SFM信号采用WHDOP定位方法。

表2 锚节点的位置坐标Tab.2 Position coordinates of the anchor nodes

在二维平面内，3个锚节点即可进行定位，本文在锚节点的选择方案为：从8个锚节点中选择HDOP/WHDOP值最小的3个锚节点进行定位。

对上述两种定位方法的在回形路径上的定位性能进行仿真，结果如图6所示。

图6 常规UWB和SFM信号定位性能仿真图Fig.6 Simulation of conventional UWB and SFM signal positioning performance

由图6可知，采用SFM-WHDOP定位方法的定位误差比采用UWB-HDOP定位方法的误差更小，定位精度更高，其中定位误差如表3所示。

表3 不同方式的定位误差Tab.3 Positioning errors in different ways

由表3可知，UWB-HDOP定位方法的定位均方根误差是0.23 m，UWB-WHDOP定位方法的定位误差是0.18 m，SFM-WHDOP定位方法下的定位误差是0.11 m，性能比UWB-HDOP方法提升52%，比UWB-WHDOP方法提升39%，故在室内复杂环境中，每个锚节点的测距误差相差较大时，采用SFM-WHDOP定位方法更能反映实际的定位误差趋势，具有更高的精度。

3.4 HDOP/WHDOP取值分布特性与定位锚节点选取

HDOP取值的理论最小值不小于1[16]，并且随着参与定位的锚节点个数增加，HDOP值单调减小。上述结论是在每个锚节点的测距精度一致的前提下得到了，而在实际室内复杂环境中，处于不同位置的锚节点伪距精度相差较大，加权因子矩阵Rρ表示锚节点归一化测距误差，由于考虑到锚节点伪距误差的变化的不确定性，更能反映真实的定位误差趋势。基于此，本文对3.3节的定位方法中的HDOP/WHDOP取值分布特性进行了研究，统计了各自取值的累计分布函数（CDF）特性，结果如图7所示。

从图7的CDF曲线可知，本文的WHDOP最小值是0.4，明显小于HDOP值的最小值，并且WHDOP值小于 HDOP最小值的概率超过 50%，也就意味着WHDOP方法对测距误差的放大倍数更小，由于考虑到锚节点伪距测量误差变化的不确定性，故此基于WHDOP定位系统的定位精度会更高。

由于 HDOP定位方法的锚节点选择方法只与锚节点的空间布局有关，而WHDOP定位方法的锚节点选择方法不仅与锚节点的空间布局有关还与锚节点的测距误差有关。在3.3节的仿真中，在某一段定位点处锚节点选择如图8所示。

图7 HDOP/WHDOP取值累计分布函数（CDF）特性图Fig.7 Cumulative distribution curves of HDOP and WHDOP values

图8 HDOP/WHDOP定位方法锚节点选择示意图Fig.8 Anchor node selection diagram of HDOP/WHDOP positioning method

图8中带数字1～8的黑色图框表示锚节点坐在的位置，带字母A、B的红色图框表示研究的定位区域。其中，在A框内HDOP方法选择的3个定位锚节点是4/5/8，WHDOP方法选择的3个定位锚节点是4/7/8。在B框内HDOP方法选择的3个定位锚节点是5/7/8，WHDOP方法选择的3个定位锚节点是2/5/7。经过分析得到，仿真中假设A/B之间存在障碍物，由于障碍物的关系，使得待定位节点在A框内接收到锚节点5的测距误差明显较大，HDOP定位方法无法识别障碍物的存在，而WHDOP方法可以根据测距误差的大小灵活选择躲避障碍物的锚节点7，故此WHDOP定位方法选择的锚节点得到的定位精度更高。同理待定位节点在B框内的时候WHDOP定位方法选择的锚节点是2而不是存在障碍物的锚节点8，此时HDOP定位方法依然存在无法躲避障碍物进行定位的劣势。故此采用加权水平精度因子作为选取锚节点定位的准则，可以赋予误差较小锚节点在位置解算过程中更大的权重，可缓解室内存在障碍物时定位精度较低的问题，可进一步提升定位系统的定位精度。

4 结 论

为了提高室内定位系统的定位精度，并且选择最优的锚节点参与定位，本文对宽带调频SFM信号的测距性能和顾及WHDOP的定位选星方式进行了相关研究，提出了一种基于SFM-WHDOP方法的高精度室内定位方法。首先仿真了常规UWB、LFM和SFM信号测距性能，证明SFM信号的测距精度更高；然后研究了在室内不同噪声环境（高斯噪声环境和瑞利噪声环境）下WHDOP定位系统的鲁棒性能，随着噪声环境复杂度的增加，WHDOP方法的鲁棒性能更强；最后仿真了常规UWB-HDOP方法与本文所提SFM-WHDOP定位方法的性能。

在回形路径下，SFM-WHDOP方法的定位误差比UWB-HDOP方法的性能提升了 50%以上。同时，采用WHDOP作为选取锚节点定位的准则，可以赋予误差较小锚节点在位置解算过程中更大的权重，缓解室内存在障碍物时定位精度较低的问题。故在室内复杂环境中，采用SFM-WHDOP方法可以实现高精度室内定位功能。后续将会对该定位方法进行硬件设计验证和实际测试。