软土地基中壁桩框架码头结构受力分析及稳定性计算方法

薛润泽，别社安，郭林林，张佩良，丁文智



软土地基中壁桩框架码头结构受力分析及稳定性计算方法

薛润泽1，别社安1，郭林林1，张佩良2，丁文智2

(1．天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 天津港航工程有限公司，天津 300457)

针对适用于软土地基的壁桩框架码头结构，对其稳定机理进行分析，并提出设计计算方法．结合壁桩框架结构自身特点，提出非均质土体中截桩力计算方法，并考虑排距对截桩力的影响．在此基础上建立该结构的水平抗滑、抗倾、整体圆弧滑动稳定性及桩基竖向承载力的分析模型和计算方法．通过工程试验对壁桩框架码头结构及其稳定性计算方法的应用可行性进行验证，并研究了排距、桩长、桩径和桩间距等因素对稳定性的影响．结果表明，试验工程的最不利滑动面经过桩身、位于抗剪强度指标较弱的地基土底面，增大排距可有效提高结构的稳定性．所提出的计算方法能够合理地反映壁桩框架码头结构的稳定机理，为该结构的工程应用提供参考依据．

双排桩结构；框架；码头；稳定性分析；极限平衡法

随着人类对海岸资源的开发，对港口工程建设及港工建筑物的多功能性不断提出新的要求，需要基于现有结构特点综合创新，开发新结构．壁桩框架结构是一种应用于海岸工程的新型双排桩结构，主要由桩基结构、框架结构及回填料组成；该结构采用整体预制的钢筋混凝土框架结构取代传统双排桩结构中的拉杆和导梁结构，具有安全耐久、经济良好、施工便捷、适用性强等特点．研究开发针对壁桩框架结构稳定性的设计计算方法对该结构的推广应用具有一定的参考价值．

目前，双排桩结构多应用于基坑工程开挖支护结构[1-3]，排距约2～5(为桩的直径)，也应用于港口工程的对拉板桩结构[4]，通过桩顶拉杆连接双排桩，并维持回填料作用下的结构稳定性．对于双排桩结构的水平承载特点，国内外学者进行了大量研究．基于桩身平衡微分方程，结合后桩水平荷载类型及桩顶约束条件，Sawaguchi[5]首先推导了双排桩结构的桩顶水平位移和弯矩计算公式．在此基础上，Ohori 等[6]建立了考虑回填料及地基土的弹塑性特性的双排桩受力计算模型．该模型直接假定泥面以上为双排桩及内部回填料的复合结构、泥面以下为受到水平土抗力的板桩结构，没有考虑排距及桩土相互作用的影响，且未考虑后方回填及回填土上部堆载作用. Lee等[7]针对排距为0.5～2.0倍桩距的双排桩支护结构建立了等效单桩计算模型，通过施加桩顶弯矩代替双排桩结构自身的抗倾及桩顶约束作用．Ye等[8]基于线弹性刚桩且桩间土体稳定的假定，对双排阻滑桩系统提出简化设计方法．Yu等[9]从施工角度出发，考虑了双排阻滑桩不同施工阶段受力特点，分别建立了前桩单独受力和双排桩共同受力两种桩身内力计算模型．Mizutani等[10]、Zhu等[11]、Wang等[12]、王星华 等[13]、丁洪元等[14]对双排桩支护结构桩身位移和弯矩分布的影响因素进行了研究，包括回填料及上部隔墙刚度、地基土抗剪强度、空间效应、排距、桩径和桩长等因素．上述成果主要集中在双排桩结构的位移和内力计算方法研究，欠缺对结构稳定性机理及相应计算方法的研究分析．此外，壁桩框架结构作为码头结构时，前、后排桩共同承受后方回填荷载，其受力模式不同于现有的对拉板桩结构．相比于双排桩支护结构，壁桩框架码头结构的排距较大，对其进行稳定性分析时需要考虑内部回填对前、后排桩的作用以及排距对其影响．

本文采用极限平衡法[15]对壁桩框架码头结构的稳定机理进行分析．基于Mohr-Columb强度理论，描述土体在破坏瞬间的静力平衡状态，定义相应的稳定性系数．结合壁桩框架结构特点，假定滑动破坏面经过桩身，提出相应的非均质土中截桩力计算方法，并考虑排距影响．通过建立壁桩框架码头结构的水平抗滑、抗倾、整体圆弧滑动稳定性以及桩基竖向承载力分析模型，提出适用于实际工程的稳定性计算方法．为验证壁桩框架结构的工程应用可行性，在天津港进行了壁桩框架码头结构的工程试验，观测结构的稳定性和桩基变形，并将理论计算结果与之对比．此外，基于工程试验的设计参数，研究结构尺度对稳定性系数的影响．

1 壁桩框架结构

壁桩框架结构[16]主要由桩基结构和框架结构两部分组成，其三维示意见图1(a)．桩基结构由两排平行布置、间距微小的预应力高强度混凝土管桩(PHC桩)构成；框架结构为整体预制的钢筋混凝土结构，由对拉桁架、水平导梁和挡墙3部分组成．当其作为码头结构使用时，结构断面如图1(b)所示，框架结构坐于软土地基表面，PHC桩穿过水平导梁内预留导槽打入软土地基，桩顶通过现浇帽梁与框架连成一体．框架内部可回填袋装砂等材料以提升结构水平承载力．每组对拉桁架包括上、下两层拉梁，拉梁连接前、后排桩共同受力和变形；拉梁间设置立柱以提升框架刚度、降低结构内力．海侧挡墙既可充当竖向岸壁供船只停泊，还可保护PHC桩免受海浪冲蚀，同时防止框架内的回填料从桩缝间漏出．

图1 壁桩框架结构

同传统高桩码头结构相比，采用壁桩框架结构能有效地加快施工进度、缩短工期、降低造价．PHC桩和框架结构均为陆上预制现场安装，可减少海上作业所需时间．框架结构在沉桩过程中充当限位导架．施工时只需完成框架定位，即可沿导梁内预留的导槽依次吊打各桩，省去传统打桩工艺中所需的打桩船租赁费用(约占打桩费用的40%,)，具有良好的经济性．当外海施工缺乏必要掩护条件时，采用打桩船沉桩时容易因风浪较大造成船身摇摆而断桩，但壁桩框架结构采用吊打工艺，仍可满足施工要求，有效延长海上作业时段窗口．

壁桩框架结构本质上是一种多层对拉双排桩结构，采用刚度更大、具备多层拉杆的框架结构替代传统双排桩结构中的拉杆和导梁，以增强结构整体性和桩基承载力．壁桩框架结构适用于软土地基，可应用于码头结构、桩基码头后方接岸结构以及防波堤结构．通过调整框架尺寸、拉梁层数、桩径、桩长、回填料及回填高度等参数，可使该结构满足不同的水深、地质条件及结构使用要求．在非自然岸线的码头建设中，需要先期修筑围埝形成陆域，后期码头工程中再对传统围埝结构进行改造；若采用壁桩框架围埝结构，则可直接作为深水高桩码头的接岸结构．利用壁桩框架结构，现已在天津建造了可靠泊2×103,t级船舶的码头结构，在山东滨州建造了5×104,t级桩基码头的后方接岸结构兼围埝结构，使用效果良好．

2 结构受力分析和稳定性计算方法

2.1 受力状态分析

壁桩框架结构的排距介于支护双排桩结构和板桩码头结构(采用锚碇板桩)之间．支护结构中忽略桩间土作用，将双排桩视作门式刚架共同受力；板桩结构中分别按单锚板桩和无锚板桩结构计算前、后排桩的位移和内力．壁桩框架结构中排距相对较大，桩间土作用不能忽略；前、后排桩之间土体破裂线相交于地面以下，内部回填料作用于后排桩的水平抗力小于被动土压力．对结构进行稳定性分析时，可将双排桩和桩间土视作整体；对单排桩进行受力计算时，需要考虑排距对土压力的影响．

以壁桩框架码头结构为例，在后方回填土自重及堆货荷载产生的水平推力作用下，前、后排桩在框架结构的约束下一同产生水平变形，同时围绕前桩轴线上某一点发生转动．框架结构的刚度较大，将显著影响桩顶至框架底部范围内的桩身变形；拉梁在双排桩间产生双点乃至多点对拉作用，同仅在桩顶处单点受拉的双排桩结构相比，有利于限制地基深处桩身水平位移、降低桩身最大弯矩．

2.2 稳定性计算方法

参考欧州标准[17]和国家标准[18]，壁桩框架码头结构可能存在以下几种稳定性失效模式：地基和桩基的复合破坏(包括水平滑动、绕前侧桩基上的一点转动倾覆)、整体失稳和桩基承载力不足．基于极限平衡理论，分别针对上述稳定性失效模式建立结构受力分析模型，并推导相应的稳定性系数计算公式．当各结构稳定性系数均大于或等于1时，结构是安全稳 定的.

2.2.1 非均质土中的截桩力计算

壁桩框架结构中桩基间距很小，构成排桩结构；结构的刚度和强度有别于重力式基础结构，不足以使破坏面位于结构底部与地基交界处，故破坏面可能产生于框架底部至桩底的任意位置处．当滑动面通过桩身时，截桩力有利于阻止临界状态下滑动面以上土体和结构的滑动趋势．基于均质土内截桩力计算模型[19]，本文提出针对非均质土的截桩力计算方法，计算图式见图2．

图2 非均质地基中截桩力计算图式

   (1)

   (2)

前、后双排桩的单宽截桩力之合为

   (3)

图3 前、后排桩间的土体破裂线

2.2.2 水平抗滑稳定性计算

由抗滑力与滑动力的比值得滑动面的水平抗滑稳定性系数为

   (4)

根据式(4)对各滑动面进行计算，水平抗滑稳定性系数最小值所对应滑动面即为最不利滑动面，应满足

   (5)

表1 分项系数取值

Tab.1 Partial coefficient values

2.2.3 抗倾稳定性计算

根据对转动点的抗倾与倾覆力矩的比值可得抗倾稳定性系数为

     (6)

且应满足

   (7)

根据式(6)对至各转动点计算，抗倾稳定性系数最小值对应最不利转动点，应满足

2.2.4 圆弧滑动稳定性计算

按平面问题考虑，假定滑动面为圆弧面，采用简单条分法计算结构的稳定性系数．计算时各个土条自身满足力平衡和力矩平衡，但不计入土条间相互作用力．针对壁桩框架结构整体破坏时可能发生截桩现象的特点，需要分别计算下述2种情况：①滑弧经过桩底土体，见图6(a)；②滑弧经过桩身，需考虑截桩力的抗滑作用，见图6(b)．整体稳定性系数定义为稳定力矩与圆弧滑动力矩之比，即

   (9)

取滑弧经过桩底和滑弧截桩两种情况中计算所得系数较小者，作为结构整体圆弧滑动稳定性系数，应满足

   (10)

2.2.5 竖向承载失稳验算

单桩竖向承载力设计值为

   (11)

桩基承载力系数应满足

   (12)

3 工程试验和稳定性分析

3.1 工程试验介绍

为验证壁桩框架码头结构的稳定性和施工建造可行性，天津港航工程有限公司在天津港进行了工程试验．该试验由12组壁桩框架码头结构组成，岸线长200,m．工程所处水域风浪掩护条件较好，可不考虑波浪作用．结构断面如图8所示，原泥面顶标高0,m，码头面顶标高为6.0,m，前侧港池设计开挖至 -4.5,m，靠泊2×103,t级船．在框架结构之下前排桩内侧抛填袋装砂以防止回填砂从桩缝中漏出．工程所在处地基土的物性指标如表2所示，浅层土为吹填软土层及海相沉积软土层，承载力低且压缩性大；深层土为粉黏土层，可作为桩尖持力层．单个钢筋混凝土预制框架结构的设计参数见表3．

壁桩框架码头工程施工现场照片见图9，主要施工步骤如下．

步骤1陆上整体预制钢筋混凝土框架结构和PHC桩．

步骤2将框架结构吊装到半潜驳上，并安装助浮钢筒；半潜驳航行至深水区后下潜，用拖轮拖带浮运框架结构至安装点；钢浮筒内注水，框架结构在自重作用下缓慢下沉座底．

步骤3利用框架结构充当桩基施工时的限位导架，将PHC桩穿过上、下导梁内预留的导槽，直接吊打PHC桩．

步骤4在导槽内灌注填缝混凝土，现浇帽梁和胸墙结构．

步骤5在框架内部及后方逐层回填块石，进行码头面层结构施工．

图8 壁桩框架结构码头工程断面(单位：m)

表2 地基土的物性指标

Tab.2 Physical property indexes of subsoil

表3 钢筋混凝土预制框架的设计参数

Tab.3 Design parameter of precast concrete frame structure

图9 试验工程施工现场

3.2 桩身位移观测

施工时在PHC桩中预埋测斜管，施工完成后在码头面通过堆放散砂的方式进行加载试验(见图10)，两次加载大小分别为23.4,kPa和39.6,kPa．桩身位移观测从框架内回填开始，持续至第2次加载完成后70,d，位移曲线如图11所示．

图10 加载试验

由图11可知，2.5～-1.5,m范围内，前桩水平位移曲线近似为直线，表明框架确实产生了限制作用；但后桩上、下导梁处位移值并不相等，表明框架范围内桩身存在转角．在第2次加载(39.6,kPa)完成后，桩身最大水平位移为68.2,mm，此后，因桩前黏性土体的固结和蠕变，桩身最大水平位移随时间推移缓慢增长至103.6,mm．

图11 实测桩身水平位移

3.3 稳定性计算结果

按照第2节中设计方法对工程试验结构的稳定性系数进行计算，结果如表4所示．桩身位移现场观测结果显示壁桩框架码头结构稳定且无断桩现象，计算结果也表明该结构满足各项稳定性要求，二者结论一致．根据理论计算结果可知，最不利滑动面位于 -12.5,m处，即抗剪强度指标较弱的土层底面处，表明壁桩框架结构破坏时确实产生了截桩现象，前文计算方法中对截桩力的考虑是合理的，且地基土竖向分层对结构抗滑稳定性计算结果具有影响．

表4 结构稳定性系数

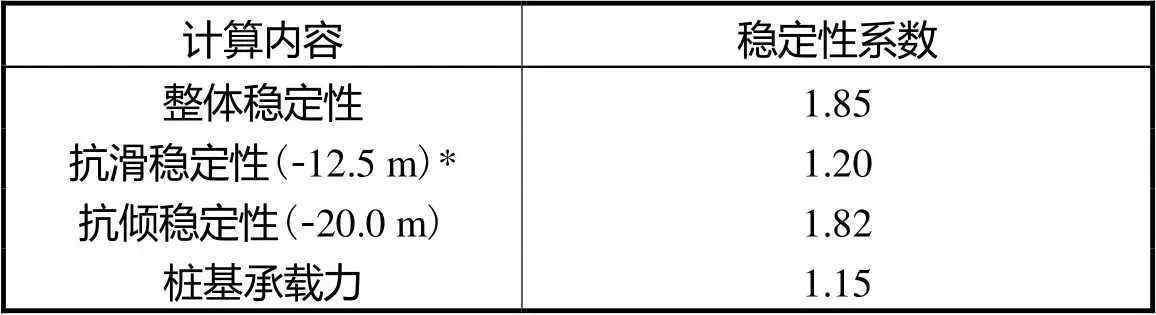
Tab.4 Coefficients of structural stability

注：“*”表示括弧内为最不利水平滑动面及转动点的高程．

4 结构参数对稳定性的影响

根据天津港工程试验的地质参数和结构尺度，基于单一变量原则，利用本文提出的计算方法研究结构尺度变化对稳定性的影响．研究对象包括框架结构的宽度(即排距)、桩长、桩径和桩间距，各变量取值如表5所示，计算所得结构稳定性系数变化趋势如图12所示．

表5 结构参数取值

Tab.5 Coefficients of structural stability

4.1 框架结构的宽度

4.2 桩长和桩径

随桩长、桩径增大，总的桩侧摩阻增大，桩基承载力系数变大．桩长为21.5,m时桩底未达到持力层，桩端承载力较差，故桩基承载力系数比桩长23.5,m时明显减小．在工程应用中，当桩底达到持力层后，与增加桩长相比，采用加大桩径比的方式更有利于提升桩基的竖向承载力．

4.3 桩间距

5 结 论

针对适用于软土地基的壁桩框架码头结构，基于极限平衡理论，考虑排桩间距和非均质土中截桩力的影响，从结构的水平抗滑、抗倾、整体圆弧滑动稳定性和桩基承载力等方面分别建立计算模型，提出一整套相应的简化计算方法，并利用该计算方法对位于天津港的壁桩框架码头结构试验工程进行稳定性验算．结合试验工程桩身位移观测结果，验证了所提出计算模型和计算方法的合理性与可行性．基于该试验工程分析结构尺度变化对结构稳定性的影响，并得到以下结论：

(1) 当地基土竖向分层时，壁桩框架结构的最不利滑动面位于抗剪强度指标较弱的土层底面处，即结构破坏时可能产生截桩现象；

(2) 增大框架结构的宽度可有效提高结构的稳定性，增大桩长、桩径均有利于提升结构的竖向承载能力，而对结构的抗滑、抗倾稳定性影响较小．

［1］ Lee C J，Chen H T，Lin E C，et al. Deformation of vertical excavation with self-supported double soldier pile wall system[C]//17. Lisbon，Portugal，2007：1427-1432.

［2］ 杜秀忠，杨光华，孙昌利，等. 双排桩支护在某水利基坑中的应用[J]. 岩土工程学报，2012，34(增1)：490-494.

Du Xiuzhong，Yang Guanghua，Sun Changli，et al. Application of retaining structure with double-row piles in a hydraulic excavation[J].，2012，34(Suppl 1)：490-494(in Chinese).

［3］ 孙涛，刘俊岩，刘燕. 双排桩支护排距的优化研究[J]. 岩土工程学报，2012，34(增1)：616-620.

Sun Tao，Liu Junyan，Liu Yan. Optimal row distance of retaining structure with double-row piles[J].，2012，34 (Suppl,1)：616-620(in Chinese).

［4］ Cui C. Nonlinear numerical study on performance of cofferdam with double-walled steel sheet piles[C] //20. Beijing，China，2010：670-673.

［5］ Sawaguchi M. Lateral behavior of a double sheet pile wall structure[J].，1974，14(1)：45-59.

［6］ Ohori K，Shoji Y，Ueda H，et al. Elasto-plastic analysis of the double sheet pile wall structure[J].，1984，9：79-88.

［7］ Lee C J，Wei Y C，Chen H T，et al. Stability analysis of cantilever double soldier-piled walls in sandy soil[J].，2011，34(4)：449-465.

［8］ Ye J，Xie Q，Zhao X，et al. Development of a practical design method for double-row anti-sliding pile system [J].，2014，19：281-293.

［9］ Yu Y，Shang Y Q，Sun H Y. Bending behavior of double-row stabilizing piles with constructional time delay[J].：，2012，13(8)：596-609.

［10］ Mizutani T，Akutagawa H，Yonezawa H，et al. Static behavior of double sheet-pile wall structures with high rigidity partitions[J].，1996，35：44-51.

［11］ Zhu Q，Mo H. Influences of reinforced soil bodies on the performance of structures with double-row piles[J].，2012，6(9)：26-33.

［12］ Wang Z H，Zhou J. Three-dimensional numerical simulation and earth pressure analysis on double-row piles with consideration of spatial effects[J].：，2011，12(10)：758-770.

［13］ 王星华，谢李钊，章敏. 深基坑开挖中双排桩支护的数值模拟及性状[J]. 中南大学学报，2014，45(2)：596-602.

Wang Xinghua，Xie Lizhao，Zhang Min. Numerical simulation and characteristic of a double-row piles retaining structure for deep excavation[J].，2014，45(2)：596-602(in Chinese).

［14］ 丁洪元，昌钰，陈斌. 软土深基坑双排桩支护结构的影响因素分析[J]. 长江科学院院报，2015，32(5)：105-109.

Ding Hongyuan，Chang Yu，Chen Bin. Factors affecting double-row piles in deep soft soil foundation [J].，2015，32(5)：105-109(in Chinese).

［15］ Wang N，Gu L. Analytic solution of elasto-plastic stress in infinite slope under uniform load[J].，1999，13(2)：197-208.

［16］ 李伟，张佩良，别社安，等. 壁桩框架结构：CN 103276691 A [P]. 2013-10-30.

Li Wei，Zhang Peiliang，Bie Shean，et al. Pile Wall Frame Structure：CN 103276691 A[P]. 2013-10-30(in Chinese).

［17］ BSI. EN 1997-1：2004Eurocode 7：Geotechnical Design-Part 1：General Rules[S]. London：British Standards Institution，2004.

［18］ 中华人民共和国交通运输部. JTS 167-3—2009 板桩码头设计与施工规范[S]. 北京：人民交通出版社，2009.

Ministry of Transport of the People’s Republic of China. JTS 167-3—2009 Code for Design and Construction for Quay Wall of Sheet Pile[S]. Beijing：China Communication Press，2009(in Chinese).

［19］ 陈万佳. 港口水工建筑物[M]. 北京：人民交通出版社，1989.

Chen Wanjia.[M]. Beijing：China Communication Press，1989(in Chinese).

［20］ Georgiadis K，Sloan S W，Lyamin A V. Ultimate lateral pressure of two side-by-side piles in clay[J].，2015，63(9)：733-745.

(责任编辑：王新英)

Mechanical Analysis and Stability Calculation Methods for Wharfs of Pile Wall Frame Structure in Soft Soil Foundation

Xue Runze1，Bie Shean1，Guo Linlin1，Zhang Peiliang2，Ding Wenzhi2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2．Tianjin Port & Channel Engineering Co.，Ltd.，Tianjin 300457，China)

The stability mechanism was analyzed for wharfs of pile wall frame structure，a structure applied to soft soil foundation，to put forward the corresponding design calculation method．Combined with the characteristics of pile wall frame structure，the calculation method of the cutting pile force under the heterogeneous soil condition was put forward with the effect of row spacing considered．On this basis，analysis models and calculation method for the structural stability of pile wall frame structure were established，including stability against level-sliding，stability against rotation，overall circular sliding stability and vertical bearing capacity of pile foundation．The engineering tests were carried out to verify the application feasibility of the pile wall frame structure and its stability calculation method，and the influences on stability were studied，such as row spacing，pile length，pile diameter and pile spacing．Results show that the most unfavorable sliding surface goes across the pile body and lies on the bottom of subsoil layer with weak shear strength index，and increasing the row spacing can efficiently improve structural stability．The proposed calculation method can reasonably reflect the stability mechanism for wharfs of pile wall frame structure，and serve as reference for engineering application.

double wall sheet-piled structure；frame structure；quay；stability analysis；limit equilibrium method

10.11784/tdxbz201611067

U656.1

A

0493-2137(2018)02-0196-09

2016-11-29；

2017-07-12.

薛润泽（1991—  ），女，博士研究生，xuerunze@tju.edu.cn.

别社安，bieshean@tju.edu.cn.

天津市科技兴海项目(KJXH2014-11).

the Project of Tianjin Marine Development with Science and Technology(No.,KJXH2014-11)．