BDS单历元算法及精度分析
2018-03-06张阳阳陈永生
张阳阳,陈永生,何 群,王 琦
(东北大学 资源与土木工程学院,沈阳 110819)
0 引言
北斗卫星导航系统(BeiDou navigation satellite system,BDS)是中国目前正在进行实施的自主研究、发展并且独立运行的卫星导航系统[1],2012年底该区域系统已经完成了组网,并且开始正式运行。它与目前国际上其他的卫星导航定位系统有着良好的兼容性和互操作性,可以为我国用户提供更为方便、准确的导航定位服务。
BDS对我国各类测绘工程的应用有着多项益处[2-3]:1)BDS卫星发送的民用伪距码精度要比全球定位系统(global positioning system,GPS)的C/A码精度高,卫星信号强度也会好于GPS,穿透力强,更能适合于在遮挡或者电磁波的干扰环境下使用;GPS卫星的L2信号上的P码经过加密,需要通过无码跟踪技术或其他的专用技术才可以捕获,这样就降低了跟踪性能,导致其载波数据容易丢失从而影响解算,而BDS卫星的B1、B2信号均为民用信号,信号强度好,而且也加强了数据的完整性。2)BDS的卫星高度角普遍比GPS卫星的大,所以在穿越电离层与对流层之间时受到的电离层和对流层延迟影响更小,也不容易受多路径效应的干扰,数据质量将有所提高;3)在BDS中地球静止轨道卫星(geosynchronous Earth orbit,GEO)的位置相对于地球是静止的,其卫星的信号往往更容易被捕捉,倾斜轨道同步卫星(inclined geosynchronous satellite orbit,IGSO)其次,而中圆地球轨道(medium Earth orbit,MEO)比较难捕获;所以相对于GPS系统全为MEO,BDS的卫星信号更容易被捕获,进而减少了接收机对卫星锁定的时间。鉴于BDS所具有的优势,在进行实时高精度单历元解算中可以提供更为有效、优质的共视卫星,提供更好的信号,在与GPS及格洛纳斯卫星导航系统(global navigation satellite system,GLONASS)等系统联测中可以提供更为完整有效的数据。
1 卫星的可见性
卫星的可见性是以某个仰角在观测点所能观测到的所有卫星数量或某时段所有观测卫星的跟踪弧段长度。分析卫星的可见性不光是判断观测条件的好坏,还会影响单历元模型中共视卫星的选取[4]。
在2016-05连续24 h对东北大学监测站进行卫星可见性分析(如图1所示)。从图中可以看出:在1时、2时、3时、4时、11时、13时、24时的时候GPS卫星数略优于BDS卫星数;在5时、9时、12时、15时、19时、22时、23时二者的卫星数相同;在6时、7时、8时、10时、14时、16时。17时、18时、20时、21时BDS的卫星数略优于GPS卫星数。24 h内的卫星总数BDS与GPS比为201∶199。在中国地区内,BDS的总卫星数在1 d内略优于GPS总卫星数,而且BDS卫星数在每小时时段内比GPS卫星数多的时候有10 h;而GPS卫星数在每小时时段内比BDS卫星数多的时候有7 h:所以在中国区域内,BDS有着优于GPS的可视卫星数。这就使得BDS更适合于应用要求共视卫星比较好的单历元算法的实时高精度定位。
2 算法原理
2.1 单历元模型
在短基线的情况下,精确GPS电码P1、P2以及L频道无线电载波L1、L2的观测方程[5-6]可以写为
(1)
式(1)中已经把卫星钟差、接收机钟差、卫星振荡器的初相、接收机振荡器初相、对流层和电离层在内的大多数误差消除。
再把式(2)线性化,在第i个历元下双差模式的误差方程一般形式为
(2)
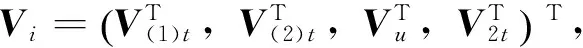
式(2)简化后可以写成
(3)
利用双差方程可以降低电离层和对流层的影响。在单历元的短基线中,可以不考虑电离层和对流层的改正项[7]。对式(3)进行分离,提取出模糊度后表示为
(4)

(5)
定义相对应的精度权阵为P;l为双差相位的观测值和计算出的值的差,可以建立相关的法方程为
(6)
可求得
(7)
dX=dX0+δX,dY=dY0+δY,dZ=dZ0+δZ。
(8)
式中:dX0为X方向变形信息初值;dY0为Y方向变形信息初值;dZ0为Z方向变形信息初值。
2.2 模糊度搜索法
在使用LAMBDA求解模糊度时,浮动解的法方程是满秩的[8],即
(9)
式中:X为坐标改正数向量;Y为双差模糊度改正数向量。而在单历元中求出的法方程却是秩亏方程,不能直接通过LAMBDA法求解[9]。为了解决单历元法方程的病态问题,适当加大了矩阵对角元素从而改善法方程的条件数。这种处理方法在数学上叫做阻尼最小二乘法[10]。将这个概念运用到单历元的解算,首先将阻尼因子替换坐标先检验的权阵Px,由基站和监测站的坐标约束(近似的坐标精度)获得。可以得
(10)

(11)
对于一般的变形监测,待求点的近似坐标值一般预测到0.5 m以内的精度,若无其他的约束条件,可以认为x、y、z3个方向的中误差同为0.5 m,然后根据式(11)计算求出权阵,在求出Px的基础上再进行一个历元的观测。由新的法方程再通过LAMBDA方法搜索模糊度,这就是阻尼LAMBDA法。
3 实验与结果分析
在抚顺西露天矿北邦的变形监测中,GPS系统的卫星数据已经成功应用于单历元的算法模型中,并已取得较好的效果。为响应国家推进BDS广泛深入应用的号召,准备在抚顺西露天矿的变形监测中应用BDS数据。为验证BDS数据应用于单历元实时差分模型的可行性、可用性,我们在监测区域分别选择2条有代表性的监测基线:1条是8001号基准点到8006号监测点,这是监测区基准点和监测点距离最近的1条基线,该条基线长大约1 km;另1条是8002号基准点到8006号监测点,这是监测区基准点到监测点最远的1条基线,这条基线长大约3 km。如图2所示。
项目实验选择在根据多年监测结果显示监测点最稳定的时间段3月初,实验参考数据(作为实验已知数据)采用国家B级网要求对这3个点进行施测,以静态后处理模式采集和下载2017年3月1日零时至3日24时72 h的2个基准点8001和8002以及1个监测点8006的GPS观测数据。单历元实验数据采集采用与B级网同一台仪器相同的时间采集,2017年3月1日零时至3日24时的2个基准点8001和8002以及1个监测点8006的BDS数据和GPS数据。数据采集时卫星截止高度角设置为10°,采样间隔为60 s,保证单历元站间能有足够的共视卫星数。这样就可在2个基准点和1个实验监测点上,均以60 s为1个历元连续采集24 h的卫星的单历元数据。
参考数据按照国家B级网数据的处理要求,进行数据处理后给出各点的3维坐标作为实验项目的已知数据(或然值),对采集的单历元BDS数据和GPS数据分别用单历元实时模型进行处理解算,每1个历元分别输出1个BDS卫星数据和GPS卫星数据处理的定位结果,这样每种卫星数据每小时获得60个定位结果,24 h分别获得1 440个定位结果数据。将得出的各历元的坐标值与参考值(按照国家B级网施测的静态后处理结果)的差值v作为改正数,采用白塞尔误差计算公式求算各历元坐标值的中误差为
(12)
在1 km基线的实验结果中,BDS和GPS在北方向、东方向、平面、高程方面精度均方根误差(root mean square,RMS)统计结果如表1所示。
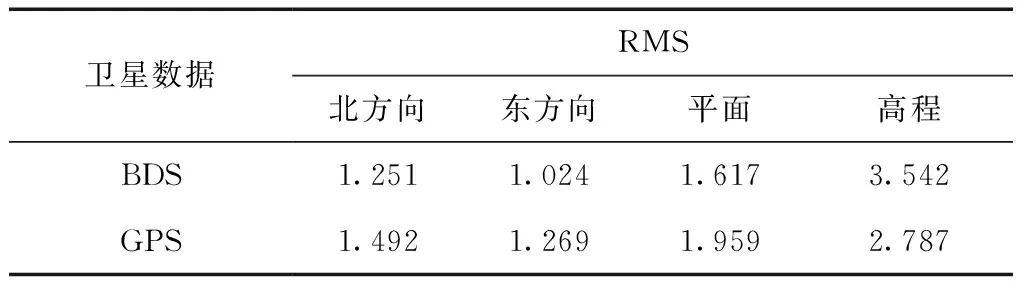
表1 1 km基线BDS与GPS精度对比 cm
根据项目要求,每天需要输出60个实时变形监测结果,这样,我们将24 h的单历元定位结果数据平均分成60个部分,仍然将差值v作为改正数,用白塞尔公式分段计算各部分的单历元观测中误差。计算所得各部分中误差结果如图3~图6所示,为BDS和GPS在1 km基线下的北、东、平面、高程方向用白塞尔公式计算的在各时间段观测的中误差。
通过单历元模型解算BDS和GPS卫星数据1 km基线结果可以看出,虽然BDS数据处理的结果精度略低于GPS的结果,但都属于一个数量级,完全可以满足抚顺西露天矿边坡变形监测的需要。
在3 km基线的实验结果中,BDS和GPS在北、东、平面、高程方向的精度统计结果如表2所示。
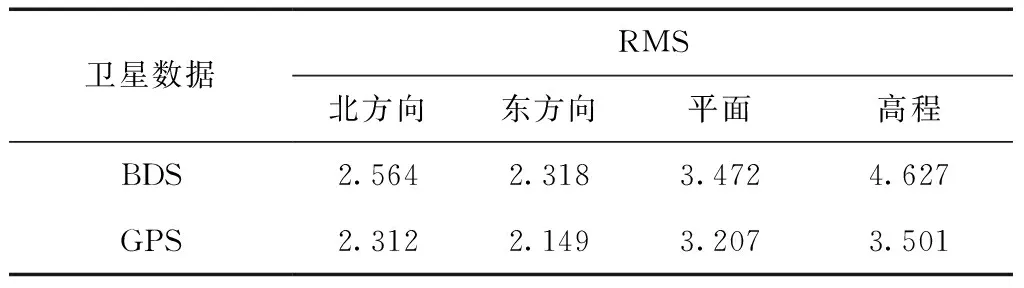
表2 3 km基线BDS与GPS精度对比 cm
以与1 km基线解算相同的方式计算所得各部分中误差结果如图7~图10所示,为BDS和GPS在3 km基线下的北、东、平面、高程方向用白塞尔公式计算的在各时间段观测的中误差。
通过单历元模型对3 km的2种卫星数据处理结果可以看出:虽然随着基准站到监测站距离的增加误差值均有所增加,精度有均所下降;但BDS和GPS差值与1 km的结果差值相比没有明显变化。
从统计的结果中可以看出BDS和GPS在北方向和高程方向上的定位精度差得比较多,这主要是因为BDS在北方向的卫星数过少、几何分布因子稍差。再对比1和3 km基线可以看出,当观测距离增加时,BDS和GPS在定位精度上都有所下降,并且在高程上BDS的精度下降得更大。这主要是因为在双差模型中,随着距离的不断增大,电离层的残差也越来越大,从而影响整周模糊度的结果。
4 结束语
目前,BDS导航卫星观测数要略好于GPS,而且在GPS信号不好时,BDS卫星的高度角相对较高,更有利于全天候的实时定位;目前BDS卫星的几何分布还不是很理想,这会对高精度实时定位带来不良影响;BDS单历元实时算法的精度目前还略低于GPS,但是处于一个数量级,可以用于变形监测。由于条件所限,该实验只做了1 h的精度比较实验,需要进行更长时间的BDS卫星数据精度测试实验,以切实服务于变形监测的工程实践。
[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.
[2] 许其凤.认识北斗建设北斗[J].中国工程科学,2014,16(8):26-32.
[3] 林超,邹劲,黄俊铭.基于北斗的高精度测量接收机在位移监测中的应用研究[J].测绘通报,2015(2):64-66,69.
[4] 刘会杰,张乃通.全球导航卫星系统的星座可见性研究[J].系统工程与电子技术,2000(5):23-25.
[5] XU G C.GPS theory,algorithm and applications[M].Berlin:Springer-Verlag,2007.
[6] 李征航,刘万科,楼益栋,等.基于双频GPS数据的单历元定向算法研究[J].武汉大学学报(信息科学版),2007,23(9):753-756.
[7] 郭际明,周命端,谢翔,等.利用DUFCOM和DC算法的GPS单历元双差整周模糊度快速确定算法[J].武汉大学学报(信息科学版),2013,38(7):813-817.
[8] 刘宁,熊永良,王德军,等.一种新的GPS整周模糊度单历元求解算法[J].武汉大学学报(信息科学版),2013,38(3):291-294.
[9] 唐波,朱俊岭,崔平远,等.基于LAMBDA方法的GPS整周模糊度解算研究[J].计算机仿真,2006(6):120-123.
[10] 刘根友,朱耀仲,韩保民.GPS单历元定位的阻尼LAMBDA算法[J].武汉大学学报(信息科学版),2004,29(3):195-197.
