卫星导航高灵敏FFT锁频环错锁检测方法

陈 杨，金 天

(北京航空航天大学 电子信息工程学院，北京 100191)

0 引言

商用接收机经常需要工作在城市峡谷、室内等信号条件非常恶劣的环境中，在这些环境下信噪比往往很低，传统接收机无法胜任[1]。为了满足在弱信号条件下的导航定位需求，人们对高灵敏卫星导航接收机进行了深入的研究，而高灵敏跟踪环路的设计是整个高灵敏接收机中非常关键的一环。在常见的高灵敏锁频环路中，高灵敏快速傅里叶变换(fast Fourier transformation，FFT)锁频环因为其良好的性能，受到了广泛的关注；但目前的研究内容大多集中在如何进一步提升FFT环路的灵敏度[2-3]以及动态性[4]上，对于高灵敏FFT环路错锁的成因以及检测问题，相关的研究还比较少。

在传统环路中，错锁的产生是因为频率误差超出了线性鉴频范围，当相干积分时间为Tcoh，且鉴频器的鉴频范围为±1/2Tcoh时，最终跟踪环路将错锁于1/Tcoh[5]。针对传统环路，文献[6]分析了错锁发生时锁频环和锁相环的状态，发现当错锁发生时I支路积分值会发生翻转，据此提出了一种利用I支路积分值翻转计数来进行错锁检测的方法，并利用仿真数据对方法进行了验证。文献[7]从最优化数字滤波器设计和锁频锁相环融合的角度，提出了一种新型的相位锁定环路(phase lock loop，PLL)，称为模糊频率辅助PLL。从仿真和实测结果来看，该环路可以有效抑制错锁情况的发生，并具有良好的动态性。文献[8]对传统的叉积鉴频方法进行了改进，将鉴频对象从2个相邻伪码周期信号变成1个伪码周期信号的相邻半个周期，由此提出了一种利用相关能量的高低来进行误锁检测的方法。但高灵敏FFT跟踪环路的锁频原理与传统环路不同，其错锁点成因以及错锁位置与传统环路有显著差别，上述方法并不能直接适用。

本文通过分析高灵敏FFT锁频环错锁原因，提出一种错锁检测方法，从检测概率和虚警率2个角度分析方法的理论性能并加以验证。

1 FFT锁频环原理

传统的数字锁频环是由模拟环路通过线性z域变换等方式得到的，变换过程本身就会导致实际环路噪声带宽大于理论带宽值，当环路预检积分时间变长时，经典数字环路参数均不再理想，将导致环路稳定性变差[9]。

不同于传统环路，基于FFT的高灵敏载波跟踪算法使用FFT频域分析方法同时辅以导航电文估计技术来替代鉴别器功能：FFT频域分析方法具有较宽的误差提取线性范围，从而有效地避免了环路非线性失真[2]；舍弃了环路滤波器，根据有无信号时FFT环路输出的序列特点来设置后验估计门限，当FFT输出峰值超出该门限时，表明算法得到了当前的频差估计。FFT锁频环的工作原理如图1所示。

假设输入信号ui(t)的伪码已经被剥离，可表示为

(1)

式中：a为幅度；D(t)为调制在载波上的数据码；fi和θi分别为输入频率和输入初相位。压控振荡器产生了正弦和余弦2路载波信号，分别与输入信号相乘，对应地可以表示为

(2)

式中f0和Q0分别为本地复制信号的频率和初相位。输入信号与正余弦弦载波复制信号相乘后分别得到同相和正交信号，通过Tcoh长度的预检测积分，这里假设积分时间内没有电文跳变，并且积分时间足够长，足以将高频成分滤除，得到I(n)和Q(n)为

(3)

(4)

则二者相加后复数相量

R(n)=I(n)+jQ(n)=aD(n)sinc (feTcoh)ej(2πfenTcoh+θe)。

(5)

式中j代表虚部。因为不同积分值中间可能会有电文跳变，送入FFT运算之前，需要对导航电文进行估计，消除符号后才能进行FFT运算。可得消除符号后的复向量为

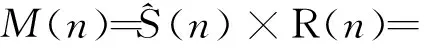
(6)

S(n)=sign(D(n)D(n-1))。

(7)

式中sign为符号函数。假设fe在期间没有发生变化，则

(8)

式中：I(n)、Q(n)、I(n-1)、Q(n-1)为由式(3)得到的第n和第n-1个积分值；Δφ为前后2个周期的相位差，即

Δφ=2πfeTcoh。

(9)

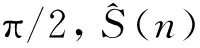
(10)

文献[2]指出有信号和无信号时，|F(k)|分别满足莱斯分布和瑞利分布，并给出了给定虚警率pF下的判决门限

(11)

(12)

2 高灵敏FFT环路错锁原因分析

对于高灵敏FFT环来说，假设做N点FFT，当频差为fe时，由前面的分析可知最终输出的fout受到频差fe、鉴频模糊误差fe,v和电文翻转值判断错误误差fe,s3者共同影响，可得

fout=fe+fe,s+fe,v。

(13)

对于传统环路来说，其输出仅仅受频差fe和鉴频模糊误差fe,v影响，这种差异也最终导致了二者错锁点的成因和位置的不同。

式(9)反映了fe与相位角Δφ之间的关系，将式(9)代入式(8)中有

(14)

结合式(7)和式(14)有

(15)

(16)

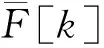
(17)

式中：当|fe|=1/2Tcoh时，fe,v可能为±1/Tcoh或0。根据不同fe条件下的fe,s和fe,v的取值，由式(13)可得

(18)

由式(18)可以看出：当|fe|=1/2Tcoh和|fe|=1/Tcoh时，鉴频器输出为0。对存在的频率误差无法鉴出，从而产生错锁现象。

与相干积分时间同样是Tcoh的传统环路相比，FFT锁频环存在2种可能的错锁类型：1/Tcoh类型错锁位置与传统环路相同，错锁原因也与传统环路相似；1/2Tcoh类型是FFT环独有的，这个特有的错锁类型并不是一个稳定的错锁类型，与高灵敏环路对电文的估计准确度有关。

3 高灵敏FFT环路错锁检测

高灵敏FFT环路拥有2种错锁类型，其中1/Tcoh错锁类型的检测方法可以参考文献[6]，而对于1/2Tcoh错锁类型，传统的检测方法在没有PLL辅助的情况下就无法正常工作，所以下面着重讨论1/2Tcoh错锁类型的检测。

在已经位同步的前提下，可以得到处于同一个电文符号下的M(n)。假设电文周期为TD，相干积分时间为Tcoh，FFT点数为N，那么一个电文周期下将会有l个积分值(l=TD/Tcoh)。当|fe|=1/2Tcoh时，M(n)的符号在一个电文周期下将会交替翻转，整个检测周期内总共将发生Cre次翻转，即

(19)

考虑有噪声的情况，假设误码概率为Pe，设置门限值d，即翻转次数大于d次即认为错锁，则其检测概率pD和虚警率pF分别为

(20)

以全球定位系统(global positioning system，GPS)L1信号为例，其电文周期TD为20 ms。当Tcoh为10 ms、FFT点数为100时，由文献[11]可以计算出不同的载噪比条件下的Pe。从式(20)得pD和pF，对应的特性曲线如图2和图3所示。

对比2图可以看出，在弱信号条件下，当20

4 实验与结果分析

为了验证错锁检测算法的效果，利用GPS采集器于2017-01采集了一组时长150 s的跑车数据，其采样率为62 MHz，中频为4.17 MHz。测试条件：使用相干积分时间为10 ms、100点的FFT锁频环，测试地点位于中关村附近(如图4所示)，测试的跑车轨迹如图5所示。这个路段高楼密集，信号环境比较恶劣，容易发生错锁。算法判决门限d设置为25。

GPSL1 12号卫星无错锁检测和有错锁检测的多普勒变化及载噪比情况见图6、图7。

由图6可以看出，无错锁检测所对应的多普勒曲线逐渐偏离有错锁检测环路的多普勒曲线，因为FFT锁频环的相干积分时间是10 ms，点数是100，所以整个环路的更新周期是1 s，整个多普勒曲线呈阶梯状下降，最终与有错锁检测的高灵敏FFT环路的输出值相差接近50 Hz，保持这个差值不变，稳定在了1/2Tcoh错锁类型。从图7可以看出与有错锁检测的环路相比，无错锁检测的环路载噪比平均低了3 dBHz左右，这是因为跟踪的载波频率与真实值相差了50 Hz。同时从图中可以看出在错锁发生后的2 s内，检测算法完成了错锁的检测工作，跟踪环路重新正确跟踪上了导航信号。

5 结束语

本文通过对高灵敏FFT锁频环的原理和错锁成因的分析，确定了FFT鉴频结果由真实的频差、鉴频模糊和导航电文剥离错误这3个方面的因素共同决定。考虑到上述因素的鉴频取值范围，发现了高灵敏FFT锁频除了具有和传统环路相同的1/Tcoh错锁类型，还具有1/2Tcoh错锁类型。根据1/2Tcoh错锁类型发生时积分值的翻转规律，提出了相应的错锁检测方法，分析了该方法在不同门限和载噪比下的虚警率和检测概率，并给出了弱信号条件下的建议门限设置方法。通过对实际卫星导航数据的测试，验证了上述方法的可行性。测试结果表明该算法可以在几十个电文周期内对错锁进行检测，进而降低错锁对环路跟踪的影响，对高灵敏度卫星导航接收机研制具有一定意义。后续可进一步开展跟踪环路错锁重新跟踪方法的研究，进一步简化错锁检测过程。

[1] SIDDAKATTE R K，BROUMANDAN A，LACHAPELLE G.Use of diversity techniques for weak GNSS signal tracking in fading environments[C]//The Institute of Electrical and Electronic Engineers(IEEE).Ubiquitous Positioning Indoor Navigation and Location Based Service(UPINLBS).New York：IEEE，2014：1-10.

[2] 王勇松.高灵敏度GNSS关键接收技术研究[D].杭州：浙江大学，2010.

[3] YAN K，ZIEDAN N I，ZHANG H，et al.Weak GPS signal tracking using FFT discriminator in open loop receiver[J].GPS Solutions，2016，20(2)：225-237.

[4] WANG X，JI X，FENG S，et al.A high-sensitivity GPS receiver carrier-tracking loop design for high-dynamic applications[J].GPS Solutions，2015，19(2)：225-236.

[5] 谢刚.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[6] 李国栋，崔晓伟，尹旭明，等.GPS接收机中锁频环频率误锁的检测[J].清华大学学报(自然科学版)，2007，47(1)：69-72.

[7] RONCAGLIOLO P A，GARCA J G，MURAVCHIK C H.Optimized carrier tracking loop design for real-time high-dynamics GNSS receivers[J].International Jouranl of Navigation and Observation，2012，2012(4)：1-18.

[8] 郑晶，王祖林，赵毅寰.扩频接收机中改进的锁频方案[J].电子对抗，2010(3)：39-44.

[9] KAZEMI P L.Optimum digital filters for GNSS tracking loops[C]//The Institute of Navigation.Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008).Savannah：IEEE, 2008：2304-2313.

[10] 奥本海姆 A V，谢弗 R W，巴克 J R，等.离散时间信号处理[M].刘树棠，黄建国，译.西安：西安交通大学出版社，2001：437-442.

[11] 何忠蛟.数字通信系统中信噪比与误码率关系的Matlab模拟[J].湖北民族学院学报(自科版)，2006，24(1)：37-38.