基于虚拟基线的相位干涉仪阵列优化设计
2019-04-27赵春雷
赵春雷,王 建
(中国船舶重工集团公司第七二四研究所,江苏 南京 211106)
0 引 言
相位干涉仪测向作为电子信号侦察领域中常用的无源测向方法,利用多个天线阵元间侦收信号的相位差进行到达方向(DOA)估计,可以在较短的天线基线条件下,实现对目标信号的高精度测向。对于采用宽带数字阵列天线的侦测系统在宽带模式下工作时,阵元间距必须满足在高频端不出现栅瓣的要求,同时阵元往往是等间隔排列的,因而限制了干涉仪基线选择的自由度。
针对单基线相位干涉仪存在的测向精度和最大无模糊测量角度之间的矛盾,长短基线、参差基线及虚拟基线[1-2]等传统解模糊方法得到了广泛应用。然而,大多数有关文献只是讨论了来波信号载频、快拍数、信噪比及通道不一致性对测向精度的影响,但对多基线相位干涉仪的阵列排布和阵元间距设计方面的研究较少[3]。本文结合实际侦测信号的工作频段、相位差测量精度以及测向精度等指标要求,同时兼顾到天线尺寸以及无模糊测角范围的限制,采用虚拟基线的配置方法进行侦收阵元选择,可以很好地避免高频端波长很短导致短基线在工程上难以实现的问题。
1 干涉仪测向原理
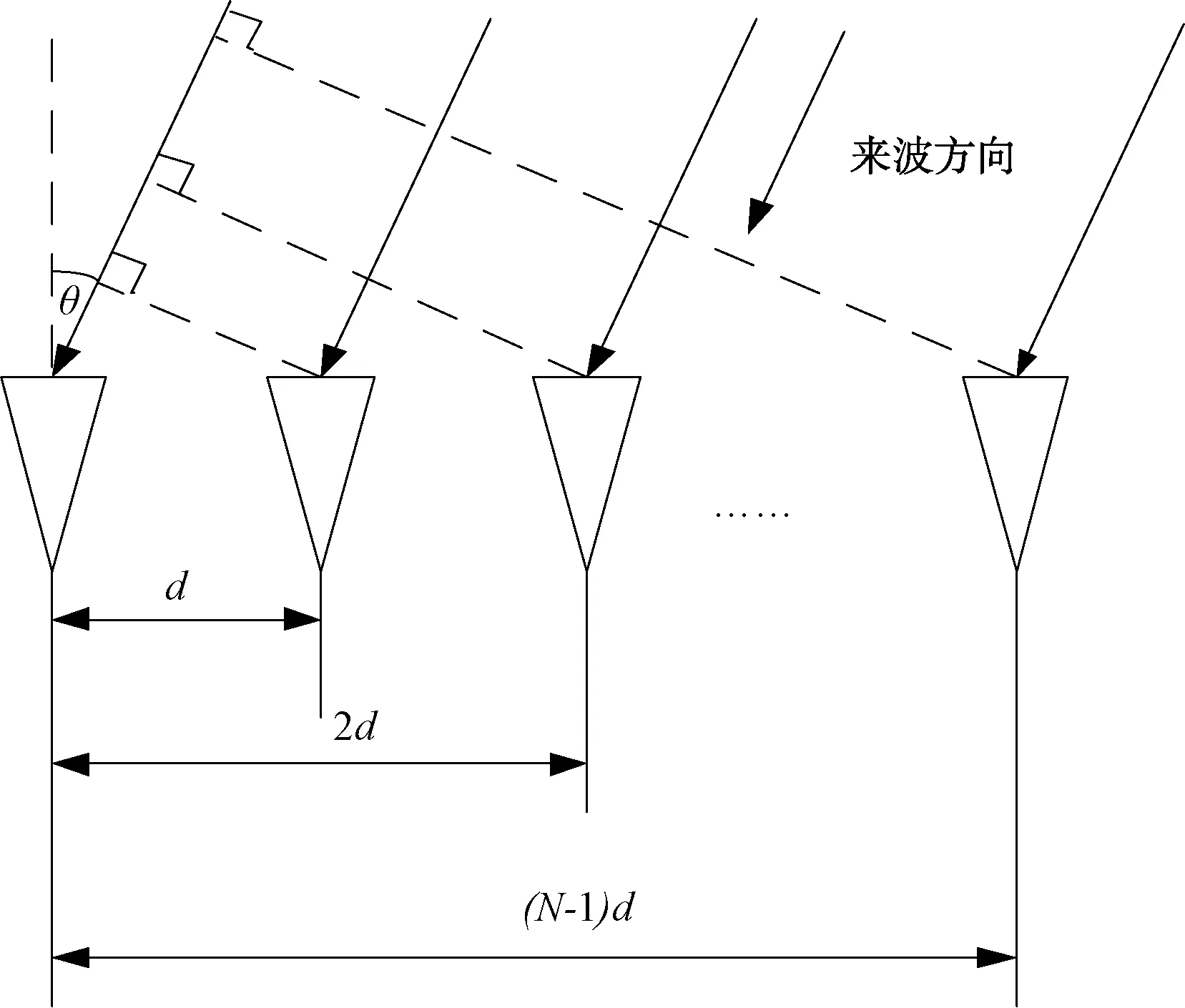
图1 多基线相位干涉仪测向原理
在图1所示的多基线相位干涉仪中,假设一波长为λ的远场辐射源信号,以θ角度入射,以天线阵元1作为参考天线单元,相邻阵元间隔为di,鉴相器输出的相位差可以表示为:
φi=ψimod2π,i=1,2,3…
(1)
阵元之间的相位差满足如下关系:
ψi/ψj=di/dj,i,j=1,2,3…
(2)
式中:ψi=2πdi·sinθ/λ,0≤φi<π,其中ψi还可以用2π的整数倍与一余数和来表示:
ψi=2πni+Δψi,i=1,2,3…
(3)
式中:ni=fix(di·sinθ/λ),其中fix(x)为对x向零取整的函数。
假设最大的可观测角限制在:|θmax|≤π/2,当可观测角取最大值±θmax时,每组基线测得的相位模糊数为±Ki=±fix(di·sinθmax/λ)。
2 基于虚拟基线的优化配置方法
基于虚拟基线的优化配置流程如图2所示,大体上可概括为以下几个步骤:

图2 基于虚拟基线的优化配置流程图
(1)确定最长基线长度
在忽略测频以及基线长度测量误差的情况下,相位干涉仪的测向误差可以表述为:
(4)
由上式可得:
(5)
式中:λmax为工作频段范围内低频所对应的波长;Δφ为相位差测量误差;θmax为最大波达角。
(2)确定最短基线长度
在实际侦测环境中,考虑到相位差测量误差的影响,为了保证最短基线不出现相位模糊,其设计的基线长度一般需要满足以下关系:
(6)
式中:λmin为工作频段范围内高频所对应的波长。
(3)配置基线比
① 根据步骤(1)、(2)计算出基线长度范围,估算出M=dmax/dmin的值。鉴于天线阵元的物理尺寸往往大于dmin,为此常常将实基线进行加减,从而构造出所需的虚拟短基线。考虑到天线各阵元间距为p·dmin,p为整数,dm+1-dm=(m+1)dmin-mdmin=dmin,因此对于三阵元的基线设计常常要在最长基线范围内,列举出所有的m+1,m组合。
② 由文献[4]可知,长基线与短基线的基线比只有满足一定的条件时,才能利用短基线去解长基线的模糊,大致可以概括为以下4种情况:实基线解实基线比例系数K1≤K1max=π/Δφ-1;实基线解虚基线比例系数K2≤K2max=π/Δφ-2;虚基线解实基线比例系数K3≤K3max=π/(2Δφ)-1/2;虚基线解虚基线比例系数K4≤K4max=π/(2Δφ)-1。在相位差误差Δφ一定时,分别算出K1、K2、K3和K4的值。
③ 初始基线数设为2,基线长度分别为(m+1)dmin、mdmin。通过计算K3值来判断dmin能否解mdmin的相位模糊,若不可解则转步骤 ④。
④ 基线数加1。顺序列出(m+1)dmin、mdmin和(M-2m-1)dmin的组合,并结合步骤②中计算出的K1、K2、K3和K4值,找出可解最长基线模糊的基线组合并输出基线配置比,继续寻找下一种组合。
⑤ 若上述组合均无法实现最长基线的解模糊,则将基线数继续加1,重复步骤 ④,直至最长基线满足解模糊要求。
3 基于虚拟基线的阵列优化设计和仿真分析
根据上一小节虚拟基线的优化配置算法,在阵元等间距条件下,针对6~18 GHz工作频段内的干涉仪基线配置进行设计,具体技术指标为:无模糊测角范围:±50°,相位差测量误差:±20°,测向精度优于1°,天线阵列按18 GHz半波长d=8 mm等间距布阵。
(1)给定阵列天线总阵元数条件下确定满足解模糊条件的最少干涉仪测向信道数:
(a)确定最长基线长度
由式(5)可得:
(b)确定最短基线长度
由式(6)可得:
dmax取248 mm,dmin取8 mm。
(c)配置基线比
① 根据dmax、dmin值,估算出M≥31。取天线阵列阵元总数为32,P≥1。
② 计算满足解模糊条件的基线比例系数
③ 初始基线数设为2,基线长度分别为(m+1)dmin、mdmin。由m+1+m=M,易得m=15,鉴于K3≤4<15,因此对于双基线而言,无法利用构造出的虚拟短基线去解最长实基线的模糊。
④ 基线数加1,此时基线个数为3个,此时将最长基线dmax依次划分为(m+1)dmin、mdmin和(M-2m-1)dmin这3段,鉴于天线实际尺寸受限,通常情况下要求m≥p=1,从m=1开始,依次列出所有的基线组合及解模糊步骤。

表1 6~18 GHz基线组合和解模糊步骤
从表1结果可以看出,当基线数为3时,共有5种基线配置组合,对比分析不难看出只有第3和第5组可以准确地解最长基线的模糊。因此,在阵元数为32的情况下,为了降低系统的设备量、节约成本,设计的基线数应不低于3才能满足解模糊条件。
(2)给定干涉仪测向信道数条件下确定满足测向精度的阵列天线最少总阵元数:
由上文分析讨论,针对6~18 GHz的辐射源信号,在满足测向精度的条件下,dmin≤8.46 mm,dmax≥247.6 mm。基于此,当给定的基线数为4时,阵列天线所需的最小阵元数:Mmin=7+8+9+7=31,此时解模糊步骤为:1(虚基线)→2(虚基线)→8(实基线)→31(实基线)。当给定的基线数为5时,阵列天线所需的最小阵元数:Mmin=7+8+9+7+7=38,此时解模糊步骤为:1(虚基线)→2(虚基线)→8(实基线)→38(实基线)。表2给出了不同干涉仪测向信道数条件下阵列天线所需的最少阵元个数。
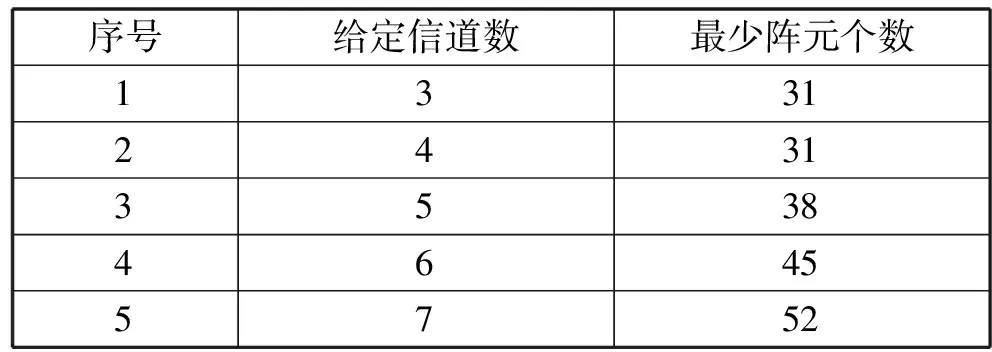
表2 给定干涉仪测向信道数条件下阵列天线所需的最少阵元个数
4 结 论
本文针对6~18 GHz频带内的辐射源信号,结合虚拟基线的优化配置算法,分别对天线总阵元数为32时满足解模糊条件所需的最少干涉仪测向信道数,以及干涉仪信道数量给定时满足测向精度所需的阵列天线最少总阵元数进行了仿真分析,进而证明了采用虚拟基线的方法对相位干涉仪阵列进行优化设计的正确性和有效性,具有一定的工程应用价值。
