SVRM方法的单天线GNSS-R土壤湿度反演

段 睿，张 波，汉牟田，杨东凯

(北京航空航天大学 电子信息工程学院，北京 100191)

0 引言

土壤湿度是农业生产、气象预报、水文观测中的重要参数[1]，因此土壤湿度探测日益成为研究热点。相比接触式土壤湿度测量方法，微波遥感测量法具有非接触、大范围、连续时间测量的优势[2]。其中，全球卫星导航系统反射信号(global navigation satellite system-reflection，GNSS-R)技术作为微波遥感的重要分支，在海风海浪、海冰海盐、溢油、土壤湿度探测等方面发挥着重要的作用。由于无需单独的发射机，且信号源丰富、时空分辨率高，越来越多研究机构开始重视GNSS-R技术[3-4]。

目前欧美国家已经对GNSS-R测量土壤湿度做了大量研究。美国国家航空航天局于2002年在新墨西哥的拉斯克鲁塞斯地区进行了著名的土壤湿度探测试验(soil moisture experiment 2002，SMEX02)，验证了反射信号对土壤湿度的敏感性，为日后的研究奠定了基础[5-8]；欧空局利用欧洲遥感系列卫星、欧洲土壤湿度和海洋盐度卫星的数据进行了系统的土壤湿度反演研究[9-10]。国内有关的研究也已取得一定的进展，中国科学院武汉物理与数学研究所、武汉大学、中国气象局、中国科学院空间中心、北京大学、北京航空航天大学等单位的学者对GNSS-R技术反演土壤湿度进行了多方面的研究并取得了有意义的成果[11]。

新兴的干涉模式测量技术(interference pattern technique，IPT)为利用GNSS-R技术反演土壤湿度提供了新的思路，在地基实验中，卫星直射信号与经土壤表面反射的信号在天线处产生干涉效应，由于卫星运动，天线接收的干涉信号是随时间波动的(即随卫星仰角的变化而变化)，由此可进行土壤湿度监测[12]。该方法使用一根右旋圆极化天线(即单天线模式)接收干涉信号，通过提取频率、幅度、相位3个干涉特征参量与土壤湿度间的关系进行土壤湿度反演，具有装置简单、适合长期定点监测的优势。由于土壤湿度对这3个参数的影响复杂，难以建立解析模型，因此目前多采用经验模型：文献[13-15]实验研究了干涉信号的相位、幅度、频率3个参数单独与土壤湿度的关系，得出了相位与土壤湿度之间的相关性最好的结论；文献[16]也对此进行了研究，指出通过多星融合能够提高3个参数与土壤湿度的相关性，但是数据处理量大，泛化性能不佳。

本文在前人工作的基础上提出利用3者的组合来反演土壤湿度的方法，并使用支持向量回归机(support vector regression machine，SVRM)来寻找土壤湿度与这3个参量的经验关系。SVRM的概念首先由文献[17]提出，这是支持向量在函数回归领域的应用，其机器学习的策略是结构风险最小化原则，专门针对有限样本的情况；因此相比传统的回归方法如神经网络方法、最小二乘法等所需的训练样本数量更少、泛化性能更好[18]。本文首先阐述单天线模式下GNSS-R测量土壤湿度的基本原理，然后结合SVRM的理论知识对利用SVRM改进GNSS-R土壤湿度测量方法的可行性进行分析。

1 单天线模式GNSS-R测量土壤湿度原理

地基条件下，单天线模式GNSS-R土壤湿度反演利用右旋圆极化天线，同时接收来自卫星的直射信号与附近土壤的反射信号。由于平台固定，架设的天线高度较低，直射与反射信号的频率近似相等，在某一时刻具有恒定的相位差，满足发生干涉现象的条件，在天线处叠加产生干涉信号。全球定位系统(global positioning system，GPS)卫星发射的直射信号为右旋圆极化信号，经过土壤反射后信号包含左旋和右旋分量，当卫星高度角小于布儒斯特角时，反射信号中右旋分量所占比例更大[19]；因此低仰角情况下干涉现象更加明显。天线接收到的干涉信号信噪比(signal-noise ratio，SNR)可以表示为

(1)

式中：Ad、Am分别为卫星直射信号和多径信号(主要指反射信号)的振幅；ψ为二者的相位差。由于反射信号的幅度小于直射信号，因此干涉信号的幅度主要取决于直射信号(如图1所示)。对干涉信号进行多项式拟合即可去除直射信号，突出多径信号带来的信号波动(如图2所示)。

SNR波形的频率取决于卫星、反射面、接收天线之间的相对位置关系(如图3所示)。一般情况下，反射面可能与水平面存在一定的倾角θ，假设卫星高度角为E，β定义为高度角与倾角之差(此即直射信号与反射面的夹角)，h为天线相对于反射面的高度，反射信号比直射信号到达天线处多传播的路程设为δ，则满足[20]

δ=2hsinβ=2hsin |E-θ|。

(2)

假设反射面与水平面之间的夹角可忽略不计(θ约等于0)，则式(2)可改为

δ=2hsinE。

(3)

由式(3)可推得，反射信号与直射信号的相位差为

(4)

式中λ为GPS信号的波长，令

x=sinE。

(5)

则有

(6)

由式(6)可知，SNR随sinE变化的频率f可写为

(7)

由此得到结论即SNR的振动频率与反射面高度呈线性关系。由于SNR的表达式中(即sinE)的变化是非线性的，故采用Lomb-Scargle变换[21]的方法对频率进行计算，从而求出反射面高度h。

文献[13]提出了干涉信号的SNR表达式为

SNR=Acos (2πfsinE+φ)。

(8)

式中：A、f、φ分别为干涉信号特征参量中的振幅、频率以及相位。由前所述，得到由多径信号(反射信号)引起的干涉振荡SNR后，代入由Lomb-Scargle变换求得的频率f，可对该信号进行最小二乘拟合，从而得到干涉振幅和相位。文献[14-15]的研究表明，3个特征参量均可用于土壤湿度的反演，且与土壤湿度呈线性关系。

2 基于SVRM的反演方法改进

SVRM将支持向量机的原理运用于回归问题，同时考虑了训练样本的拟合性和复杂性，这使得SVRM模型兼具精确性与适用性[22]。文献[23]中详细地给出了SVRM的原理。

在实际的土壤湿度实验中，对采集到的卫星信号进行处理，得到的干涉特征参量与实测土壤湿度之间的线性相关特性很难达到极好的程度，而且3者很难同时与土壤湿度呈现出较好的线性相关特性。因此将GNSS-R干涉测量技术运用于实际的土壤湿度测量还存在一定的困难。为了解决测量精度有限、反演模型稳定性差的问题，考虑将反演得到的3个干涉特征参量全部运用于土壤湿度反演模型中去，实现相位-幅度-频率联合测量土壤湿度。

具体的实现方法是：采用常用的ε-SVRM模型，将相位φ、幅度A、频率f作为ε-SVRM输入变量x的3个维度，即x=(φ,A,f)；将实测土壤湿度值作为输出变量y。核函数的选取是模型是否有效的关键因素之一，实际应用中常用的核函数有径向基核函数(radial basis function，RBF)、多项式核函数、线性核函数、多层感知器(Sigmoid)核函数等。本文选用普适性最好的RBF核函数。惩罚参数C的选取同样对模型有重要影响：C选得过大即惩罚严厉时，会出现“过学习”的现象，模型泛化性能下降；C太小即惩罚太宽松时，训练误差明显增大，此时出现“欠学习”的现象。同时参数ε、γ的选择也会从不同的方面对模型的准确性、泛化性产生影响。基于SVRM的单天线模式GNSS-R测量土壤湿度模型见图4。

3 实验与结果分析

3.1 实验数据采集

本文利用了文献[24]提供的实验数据。实验场地位于法国西南部图卢兹市旁的拉马斯屈埃尔的一处大豆种植地(43°29′14.45″N，1°13′44.11″E)。该地区属于温带气候，根据当地气象站的监测数据，年平均降雨量约为600 mm，春季降雨量最大达80 mm，夏季最小为32 mm。

实验进行于2014-02-04—2014-03-20共45 d。数据采集设备为Leica GR25接收机以及AR10天线，以1 Hz的频率采集GPS卫星信号。由于GPS L1频段比L2频段的信号更强，本实验采用 L1频段的信号进行数据处理。用卷尺测得天线高度为1.70 m。在实验地点架设天线处附近采集了5份土壤样本，对其成分进行分析，得到该地土壤中砂土占18 %、黏土和粉土各占41 %，田间持水量为48 %。

为了检验由GPS信号反演得到的土壤湿度的准确性，实验场地配备了一整套气象传感器，用以监测实验期间该地的降雨、温度以及土壤湿度[24]。在距离架设天线处几米的地方放置了2个ML3土壤湿度探头，插入土壤的深度分别为2、5 cm，每间隔10 min记录一次土壤湿度值。在实验进行期间，2 cm探头测得的土壤湿度值在10.10 %～15.95 %，5 cm探头测得的数据则在23.21 %～29.87 %。

3.2 实验数据处理

卫星高度角较小时干涉现象更加显著，但在卫星高度角太小时，信号采集易受远处树木、建筑等的影响，因此本实验截取了卫星高度角在5°～30°之间的干涉信号的SNR数据进行后续处理。偶尔出现数据采集中断较长时间的情况时，可能恰好影响了该时间段内某些卫星在低仰角区间的信号采集，在后续信号处理中将舍去受影响卫星的该段数据。

对采集到的卫星数据进行处理，可求出实验期间每日接收到的各卫星干涉信号对应的相位φ、幅度A、频率f，将这些反演结果存储并作为SVRM的输入数据。通常1颗GPS卫星在符合低仰角条件下的时间较短，短时间内土壤湿度实测值的变化很小；因此可将该时间段内土壤湿度值视为定值。将用于反演的低仰角时间段卫星数据所对应时间段以内测得的土壤湿度值提取出来，求得该段时间内的土壤湿度实测平均值，作为SVRM的输出数据。

对某颗可被观测且信号接收条件良好的卫星而言，假设实验期间没有被数据采集中断的事件影响，每天可获得一段信号质量良好的低卫星高度角SNR振荡曲线，对应一组反演得到的干涉特征参量φ、A、f，以及该段SNR曲线所对应时间段内由土壤湿度传感器测得的土壤湿度值的平均值。因此对于某颗卫星来说，实验期间共可获得45组样本，构成了利用ε-SVRM进行机器学习的训练集及测试集。考虑到实验地点的地理位置以及信号接收处理的情况，后文将以结果较为理想的GPS PRN26卫星的数据为例，进行更详细的分析。

将这45组样本随机地划分为训练集、测试集，验证SVRM对反演模型性能的提升。经过多次测试不同的训练集与测试集的比例对反演结果的影响，大致可以确定，当训练集样本与测试集样本的比例约等于3∶1时效果最佳，这个比例也是SVRM在实际应用中较常被采用的。以GPS PRN26卫星为例，将该卫星的数据处理后得到的45组样本划分为33组训练集样本以及12组测试集样本，二者互斥。同时为了确定不同的ε-SVRM参数对模型的影响，采用遍历的方法在一定范围内测试并最终确立最佳的“-c”、“-g”、“-p”参数的值(分别对应C、γ、ε参数)；参数的选取考虑了第2节中讨论的注意事项，尤其关注了参数C的选取(不宜过大或过小)。

为了排除随机划分训练集、测试集对反演模型的影响，本文进行了100次独立实验将45组样本随机地划分为训练集与测试集，分别对训练集进行SVRM训练，得到的模型用测试集数据测试其性能。

3.3 结果分析

以GPS PRN26卫星为例，求得的45组数据中φ、A、f与2 cm深处探针测得的土壤湿度之间的相关系数分别为0.531 5、-0.871 5、-0.830 4，与5 cm处土壤湿度的相关系数分别为0.513 0、-0.928 2、-0.795 6；其中利用幅度反演得到的土壤湿度与2 cm处土壤湿度的平均误差绝对值为0.691 4 %，RMSE为0.829 8 %，与5 cm处土壤湿度的平均误差绝对值为0.590 8 %，RMSE为0.701 1 %。图5所示为PRN26卫星信号反演得到的与5 cm处土壤湿度的关系图。可以看出，本实验中与土壤湿度相关性最佳的干涉特征参量是幅度A。

独立、随机地对45组样本划分100次后进行SVRM机器学习，对100次结果取平均可知：SVRM反演所得的2 cm深处土壤湿度与实测数据之间的相关系数为0.961 5，测量误差的绝对值平均为0.362 7 %；5 cm深处土壤湿度与实测数据间的相关系数为0.973 4，测量误差的绝对值平均为0.349 1 %。2种情况下，利用SVRM对原土壤湿度反演模型进行改进后都能获得较好的土壤湿度测量精度，如表1所示。

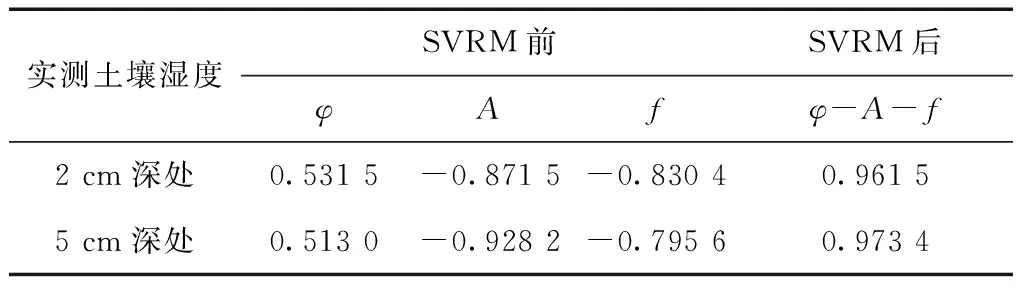
表1 不同反演结果与土壤湿度的相关系数

具体地，以5 cm深处土壤湿度测量值作为SVRM输出数据为例，由于划分训练集、测试集采用的是随机划分的方法，少数不合理的划分策略会显著降低改进后模型的测量精度。

这100次随机划分后的反演结果如图6所示，其中：有7次划分使得测试集中反演的土壤湿度值与测量值之间的相关系数达到了0.99以上，其中最大相关系数达到0.994 3；有43次使得相关系数大于0.98；相关系数最小仅为0.872 2。

分析训练集、测试集的划分策略与模型效果之间的关系可知，如果划分训练集与测试集时太过极端，使得测试集中样本的土壤湿度范围与训练集样本的土壤湿度范围有较大差异，就会导致训练不合理，泛化性能下降。因此，将土壤湿度实测值能够较均匀地涵盖整个实验周期内土壤的湿度范围的样本取出作为训练集时，得到的模型更有利于土壤湿度的测量。通过人为地划分训练集与测试集，可以使SVRM改进的单天线模式土壤湿度测量技术的精度大幅提升，测量值与真实值的相关系数可以达到0.994 3甚至更高，测量误差的绝对值可控制在0.206 0 %，如图7所示。

4 结束语

本文提出了一种基于SVRM的单天线模式GNSS-R土壤湿度测量方法，给出了数据处理的基本流程，利用实地的土壤湿度测量实验所得的数据对该方法进行了验证，结果表明：传统的利用GNSS-R单天线技术测量土壤湿度是可行的，但其测量精度有限，其中利用幅度反演土壤湿度时反演结果与实测值的相关系数为-0.928 2，平均测量误差的绝对值为0.590 8 %；SVRM改进的土壤湿度测量方法能够有效地提升测量精度，反演值与实测值间的相关系数可达0.994 3，平均测量误差的绝对值可控制在0.206 0 %。在机器学习的过程中，通过对训练集、测试集进行更多合理划分的尝试，土壤湿度反演模型的精度可以进一步提升。为了验证改进后模型的泛化能力，本文后续将进行更长期的实验，并将土壤表面的植被影响等因素考虑进来。

[1] 严颂华，龚健雅，张训械，等.GNSS-R测量地表土壤湿度的地基实验[J].地球物理学报，2011，54(11)：2735-2744.

[2] HEGARAT-MASCLE S L，ZRIBI M，ALEM F，et al.Soil moisture estimation from ERS/SAR data：toward an operational methodology[J].IEEE Transactions on Geoscience & Remote Sensing，2003，40(12)：2647-2658.

[3] 杨东凯，张其善.GNSS反射信号处理基础与实践[M].北京：电子工业出版社，2012：81.

[4] 严颂华，张训械.基于GNSS-R信号的土壤湿度反演研究[J].电波科学学报，2010，25(1)：8-13.

[5] 毛克彪，王建明，张孟阳，等.GNSS-R信号反演土壤水分研究分析[J].遥感信息，2009，2009(3)：92-97.

[6] 王迎强，严卫，符养，等.机载GPS反射信号土壤湿度测量技术[J].遥感学报，2009，13(4)：670-685.

[7] CROSSON W L，LIMAYE A S，LAYMON C A.Parameter sensitivity of soil moisture retrievals from airborne L-band radiometer measurements in SMEX02[J].IEEE Transactions on Geoscience & Remote Sensing，2005，43(7)：1517-1528.

[8] MASTERS D，AXELRAD P，KATZBERG S.Initial results of land-reflected GPS bistatic radar measurements in SMEX02[J].Remote Sensing of Environment，2004，92(4)：507-520.

[9] KERR Y H，WALDTEUFEL P，WIGNERON J P，et al.Soil moisture retrieval from space：the soil moisture and ocean salinity(SMOS)mission[J].IEEE Transactions on Geoscience & Remote Sensing，2001，39(8)：1729-1735.

[10] KERR Y H，WALDTEUFEL P，RICHAUME P，et al.The SMOS soil moisture retrieval algorithm[J].IEEE Transactions on Geoscience & Remote Sensing，2012，5(5)：1384-1403.

[11] 邹文博，张波，洪学宝，等.利用北斗GEO卫星反射信号反演土壤湿度[J].测绘学报，2016，45(2)：199-204.

[12] RODRIGUEZALVAREZ N，BOSCHLLUIS X，CAMPS A，et al.Soil moisture retrieval using GNSS-R techniques：experimental results over a bare soil field[J].IEEE Transactions on Geoscience & Remote Sensing，2009，47(11)：3616-3624.

[13] LARSON K M，SMALL E E，GUTMANN E D，et al.Use of GPS receivers as a soil moisture network for water cycle studies[J].Geophysical Research Letters，2008，35(24)：851-854.

[14] ZAVOROTNY V U，LARSON K M，BRAUN J J，et al.A physical model for GPS multipath caused by land reflections：toward bare soil moisture retrievals[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing，2010，3(1)：100-110.

[15] CHEW C C，SMALL E E，LARSON K M，et al.Effects of near-surface soil moisture on GPS SNR data：development of a retrieval algorithm for soil moisture[J].IEEE Transactions on Geoscience & Remote Sensing，2014，52(1)：537-543.

[16] ROUSSEL N，FRAPPART F，RAMILLIEN G，et al.Detection of soil moisture variations using GPS and GLONASS SNR data for elevation angles ranging from 2° to 70°[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing，2016：1-14.

[17] VAPNIK V N.The nature of statistical learning theory[J].IEEE Transactions on Neural Networks，1995，8(6)：988-999.

[18] 杨磊，吴秋兰，张波，等.SVRM辅助的北斗GEO卫星反射信号土壤湿度反演方法[J].北京航空航天大学学报，2016，42(6)：1134-1141.

[19] 万玮，李黄，洪阳.作为外辐射源雷达的GNSS-R遥感多极化问题[J].雷达学报，2014，3(6)：641-651.

[20] BILICH A，LARSON K M，AXELRAD P.Modeling GPS phase multipath with SNR：case study from the Salar de Uyuni，Boliva[J].Journal of Geophysical Research Atmospheres，2008，113(4)：317-323.

[21] GLYNN E F，CHEN J，MUSHEGIAN A R.Detecting periodic patterns in unevenly spaced gene expression time series using Lomb-Scargle periodograms[J].Bioinformatics，2006，22(3)：310-316.

[22] 苏高利，邓芳萍.关于支持向量回归机的模型选择[J].科技通报，2006，22(2)：154-158.

[23] SMOLA A J，SCHÖLKOPF B.A tutorial on support vector regression[J].Statistics &Computing，2004，14(3)：199-222.

[24] ROUSSEL N，FRAPPART F，RAMILLIEN G，et al.Detection of soil moisture content changes by using a single geodetic antenna：the case of an agricultural plot[EB/OL].[2017-02-18].https://www.researchgate.net/profile/Jose_Darrozes3/publication/273663053_Detection_of_soil_moisture_content_changes_by_using_a_single_geodetic_antenna_The_case_of_an_agricultural_plot/links/55082f420cf27e990e093414/Detection-of-soil-moisture-content-changes-by-using-a-single-geodetic-antenna-The-case-of-an-agricultural-plot.pdf.