DGPS加速度测量及试验验证

陈 铭，武若楠，胡佩达，吴秋平

(清华大学 精密仪器系，北京 100084)

0 引言

重力场是一种反映地球特性的重要物理场，它一方面能揭示地球内部的结构与成分，另一方面也影响着地球上的物理现象；因而重力场的测量有重要意义。重力场测量有地面测量法、卫星重力测量法、海洋重力测量法与航空重力测量法等方法：地面测量精度高，但是需要测量人员逐点测量，成本高且效率低；卫星重力测量能对全球重力场进行测量，效率很高，但分辨率低；海洋重力测量实验精度、分辨率都符合要求，但由于其仅能测量海洋的重力场，仍具有局限性；航空重力测量方法具有分辨率高、测量高效并且适应绝大多数地形的优点，成为重力测量领域中一种有效的方法[1]。

航空重力测量的原理是利用重力仪测量重力加速度以及运动加速度在内的所有加速度，再减去运动加速度，得到重力加速度值。全球定位系统(global positioning system，GPS)差分载波相位技术发展成熟后，运动加速度测量主要使用该方法。在中高分辨率的条件下，差分GPS(differential GPS，DGPS)载波相位技术测量的运动加速度精度能达到毫伽级，是目前航空重力实验中运载体加速度测量的最佳选择。

在DGPS加速度测量方法出现前，重力仪的运动加速度补偿主要依赖多普勒雷达或者激光高度仪。随后气压高度计、雷达高度计等技术也相继被应用于加速度测量。这些加速度测量方法的精度均低于10 mGal，无法满足高精度海空重力仪的要求。20世纪90年代以来，GPS载波相位差分技术逐渐发展成熟，DGPS因为其在位置、速度、加速度测量中的高精度与稳定性，被普遍运用于海空重力测量领域。

载波相位差分技术测量加速度技术主要可分为2类：一类为位置微分法，通过载波相位差分求出位置，再对位置2次微分求出载体运动加速度[2-4]；另一类为载波相位直接法，对载波相位差分后直接进行2次微分，进而求出载体运动加速度[5-7]。位置微分法要求位置有极高的位置精度与连续性。利用载波相位DGPS求解位置时，需要计算整周模糊度。在长基线情况下，整周模糊度的计算并不简单，如果加速度测量中整周模糊度有变化，那么2次微分后将对加速度测量值产生很大误差。在长时间的加速度测量中，GPS卫星的星座会产生变化，这也会使加速度测量产生误差。定位解算大多数使用的是现有的商业软件，如Waypoint GrafNav，导航定位的细节保密，无法深入研究。载波相位法不需要解算位置，直接使用载波相位值的微分求解加速度，避免了求解精确的位置。同时还能对卫星进行加权最小二乘，解决星座变化的问题[1]。故本文使用载波相位直接法计算加速度。

精确评估DGPS载波相位测量加速度方法的精度，目前仍是难点，其中的关键问题在于缺乏参考加速度。现在主要的评估方法有静态实验与航空重力实验法[8]：静态实验测量静止时GPS天线的加速度、加速度输出量即为加速度测量误差，由于实际加速度测量环境为动态，该评估方法欠缺说服力；而航空重力实验比较的是不同天线独立测量得到的加速度值，利用不同测量值之间的差异衡量加速度测量精度，缺乏加速度真值。

本文设计了动态转台实验来验证DGPS的加速度测量精度，通过将GPS天线固定在转台上并随之转动，在天线相位中心处会产生大小稳定的向心加速度；比较GPS载波相位测得的加速度的模与基准向心加速度的模，就能评估加速度测量方法的精度。

1 基于DGPS的加速度测量技术

接收机接收到的GPS载波的相位与接收机到卫星的视线距离有关。利用载波相位的2次微分能够计算得出接收机到卫星的视线加速度。与定位算法类似，只要可观测卫星数量足够就能计算出接收机和卫星的相对加速度。卫星的加速度可以通过广播星历或事后精密星历求出。

1.1 速度计算

图1所示为地球、卫星以及接收机之间的位置关系。图中SV表示空产晨飞行器(space vehicle)，即卫星。

载波相位直接法计算加速度的基本方程为

(1)

对式(1)微分，得

(2)

(3)

(4)

载波相位与视线距离关系为

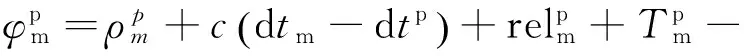
(5)

对式(5)进行微分，如果没有发生周跳，将多路径误差与相对论效应误差都合并到噪声项，可得

式中带微分符号的为相关量的一阶微分项。为了消除接收机与卫星的误差，引入参考基站k与卫星q，可得双差观测量

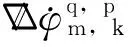
(7)

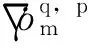
(8)

对于卫星q，由式(4)和式(8)相减得

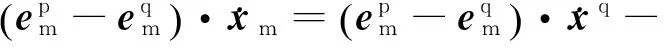
(9)

联立式(8)与式(9)，当可观测卫星大于4颗时，就能计算出接收机的速度。

1.2 加速度计算

对式(2)再次微分，得

(10)

又有

(11)

所以有

(12)

对于卫星q，也能得出类似或(2)的等式，将卫星φ、q得出的2等式相减得：

(13)

对式(8)微分得：

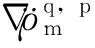
(14)

联立式(13)与式(14)，可以计算得出接收机的加速度。

当可见卫星大于4颗时，需要采用最小二乘法计算加速度。实际应用中，卫星的信号质量不尽相同，卫星的仰角、方位角等会影响信号质量，造成载波相位误差。如果简单将各个卫星的信号无差别使用，那么不能获得高精度加速度测量结果。使用加权最小二乘法能解决这一问题，在使用加权最小二乘法计算加速度时，如果使用的加权矩阵为各个卫星载波相位误差的协方差矩阵的逆矩阵，那么就能得到方差最小的结果[1-2]。

当卫星信号发生周跳时，载波相位2次微分后就会产生跳变，引起很大的加速度测量误差；因此在对卫星信号进行处理前，需要检测连续的信号中是否存在周跳[9]。

在航空重力测量领域，由于接收机噪声及其他噪声的影响，未经处理的加速度值误差量级为百毫伽级，远远不能满足应用需求。这些噪声主要集中在高频段，而重力信号则集中于低频段；所以在测得初始加速度后，还要进行低通滤波，获取高精度的加速度。滤波器的设计对加速度的计算精度影响显著。滤波器的通带波动率影响真实加速度信号的提取，而高频衰减率则影响噪声的抑制效果。使用Remez算法计算的切比雪夫一致逼近交错点组，与理想滤波器之间的偏差最小，能够满足通带波动率与高频衰减率的要求；因此本文使用Remez算法进行有限冲击响应(finite impulse response，FIR)低通滤波器设计[10-11]。给定低通滤波器的截止频率、高频衰减率与通带波动率后，能通过Remez算法计算得出滤波器系数。

2 实验与结果分析

为了验证DGPS载波相位测量加速度算法的精度，本文设计了转台实验。实验中将GPS天线固定在转台上，转台提供旋转角速度，GPS天线会产生向心加速度；如果转台的角速度精度高，那么此向心加速度可以作为加速度基准。利用加速度测量算法对这一加速度进行测量并与加速度基准进行对比，就能验证算法的准确性。

2.1 实验方案

动态实验利用旋转台完成。将GPS天线放置于转台上，步进电机驱动转台转动。转台转动时会产生向心加速度，使用GPS对这一加速度进行测量并同基准加速度对比，就能验证GPS测加速度算法的准确性。参考加速度通过转台转动的角速度以及GPS天线离转台中心的距离可以算出。

如图2所示，实验开始时，将GPS移动天线固定于旋转臂上，将旋转臂固定于转台上。同时在旁放置GPS基站天线，基站天线在实验过程中始终保持静止。启动转台，待转台转动平稳后开始记录GPS移动天线与基站天线的载波相位数据。转台的旋转周期可以设置为160～240 s，当旋转半径为0.5 m时，GPS移动天线相位中心处的向心加速度为30～70 mGal。转台平稳转动1 000 s后，可以获得足够的载波相位数据，从而计算出GPS移动天线的加速度。

利用载波相位测量得到的加速度值是矢量值，坐标系为地心地固(earth-centered earth-fixed，ECEF)坐标系。基准加速度为转台的向心加速度值，通过角速度的平方乘以旋转半径获得，为标量值。因此衡量加速度测量的精确度，通过对比测量加速度的模与基准加速度评估。

2.2 实验设备

实验设备为2套GPS天线与接收机、高精度旋转台与控制器、旋转臂、射频电滑环。高精度旋转台与控制器提供动态实验所需旋转运动，旋转角速度的精度直接影响基准加速度的精度。旋转臂将GPS移动天线固定在转台上，增加天线的旋转半径，以获得更高的向心加速度。由于移动天线一直旋转，连接移动天线的射频线需要通过射频电滑环连接至接收机。

实验使用的转台为北京卓立汉光公司Rauk200型号转台，控制器为该公司MC600。转台台面直径200 mm，中心最大载荷50 kg。转台通过步进电机驱动，配备圆光栅测量旋转角度实现闭环控制。转台具体参数如表1所示。

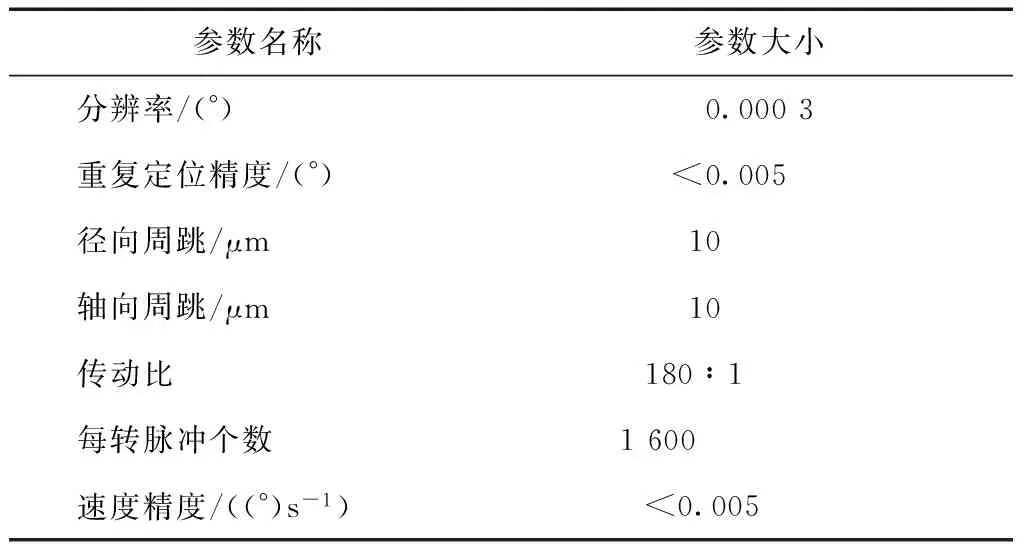
表1 转台参数

实验使用的GPS接收天线为Novatel公司GPS-703-GGG天线，接收机为Novatel公司的flexpak 6接收机。GPS天线与接收机的参数如表2所示。

表2 GPS天线与接收机参数

在动态实过程中，GPS天线持续旋转，GPS卫星的方位角因此不断改变。GPS-703-GGG天线相位中心稳定，不会因为旋转导致飘移，保证了动态实验的精度。

2.3 精度分析

动态实验的精确度由基准加速度与实际加速度的差值决定。动态实验的基准加速度值通过设定的角速度值与旋转半径计算。主要误差因素有转台设定运动角速度与实际运动角速度的误差，旋转臂、转台与GPS天线的加工误差带来的旋转半径误差。

基准加速度

(15)

式中：wd为设定的转台旋转角速度；r为GPS天线相位中心旋转半径。

在实际的动态试验中，实际角速度与设定的角速度会有误差，造成基准加速度与实际加速度的误差，即

(16)

式中：w为实际旋转角速度；ar为实际旋转加速度。

忽略2阶小量，则加速度误差为

Δa=2wd·Δw·r。

(17)

转台的角速度精度Δw为0.005(°)/s，实验中转台的角速度为2.250～1.500(°)/s，旋转半径为0.5 m，这部分造成的加速度误差为0.2～0.3 mGal。

由于天线、转台、旋转臂等加工定位的误差，实际GPS天线旋转半径与理论旋转半径之间存在误差。根据各部件的尺寸公差情况，这一误差大概为3 mm。基准加速度

ad=w2·rd。

(18)

式中rd为理论旋转半径。

考虑旋转半径误差，实际加速度

ar=w2·rr=w2·(rd+Δr)。

(19)

式中：rr为实际半径；Δr为半径误差；w为角速度。则加速度误差

Δa=w2·Δr。

(20)

实验中转台角速度为2.250～1.500(°)/s，旋转半径造成的误差为0.2～0.4 mGal。

综上，转台实验基准加速度与实际加速度的累计误差大致为0.5 mGal；而GPS测加速度算法精确度要求为1 mGal：该实验能够评估加速度测量的精度。

2.4 结果分析

在2 d时间进行了4组实验：第1天2组实验转台旋转周期分别为160与200 s，实验时长50 min；第2天2组实验转台旋转周期为200与240 s，实验时长40 min。

动态试验中，转台水平放置于水平面上，GPS天线因此也在水平面转动。GPS天线向心加速度指向旋转中心，且在水平面内转动；因此GPS天线的加速度在东与北方向的分量按照正弦曲线变化，且2个方向分量存在90°相位差。在垂直方向，由于GPS天线没有严格调水平，所以仍然存在加速度分量。转台周期160 s时东北地3方向加速度分量经过低通滤波后如图3所示，滤波器高频衰减率为-100 dB，通带波动率为0.01 dB；可以看出，加速度测量值在东北地3方向分量符合预期。

转台周期为160、200、240 s时，基准加速度分别为77.11、49.35、34.27 mGal。表3～表6为4组GPS加速度测量算法实验的结果，其中均值数据为测量得到的加速度的模的均值，标准差为加速度的模的标准差。

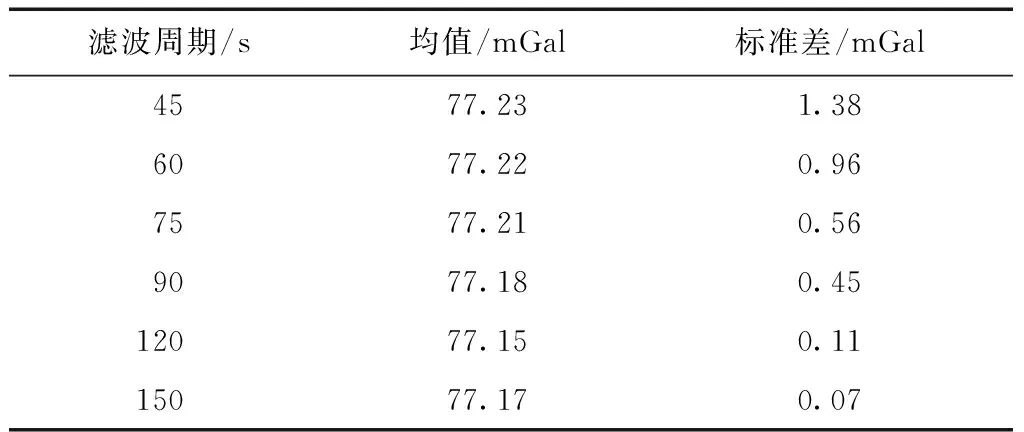
表3 转台周期160 s时加速度(真值为77.11 mGal)

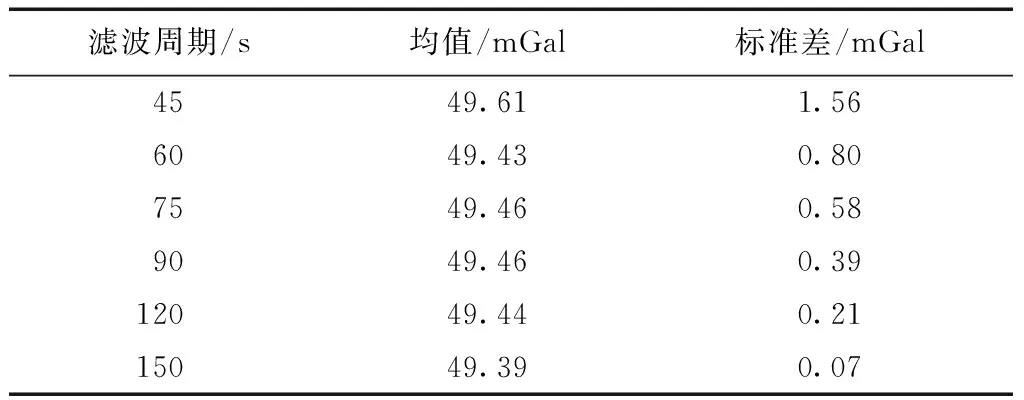
表4 转台周期200 s时加速度(真值为49.35 mGal)

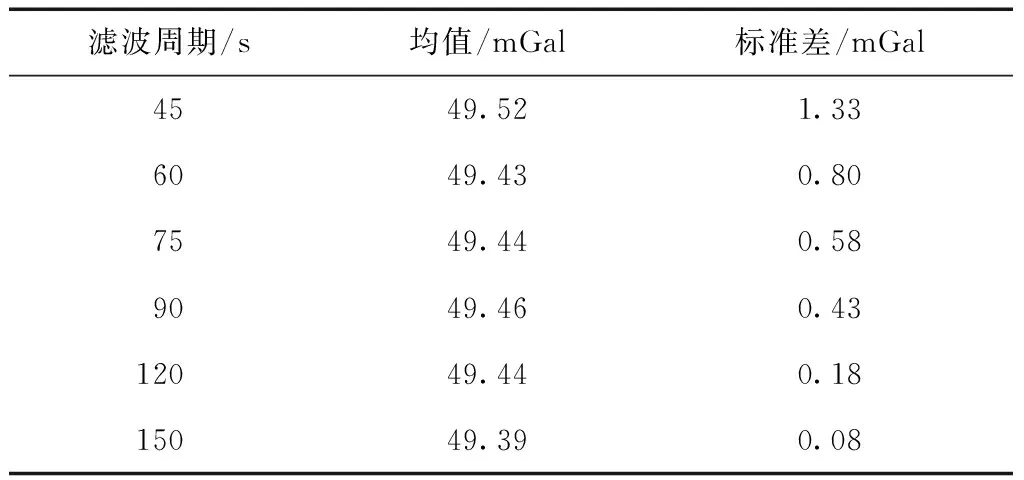
表5 转台周期200 s时加速度(真值为49.35 mGal)

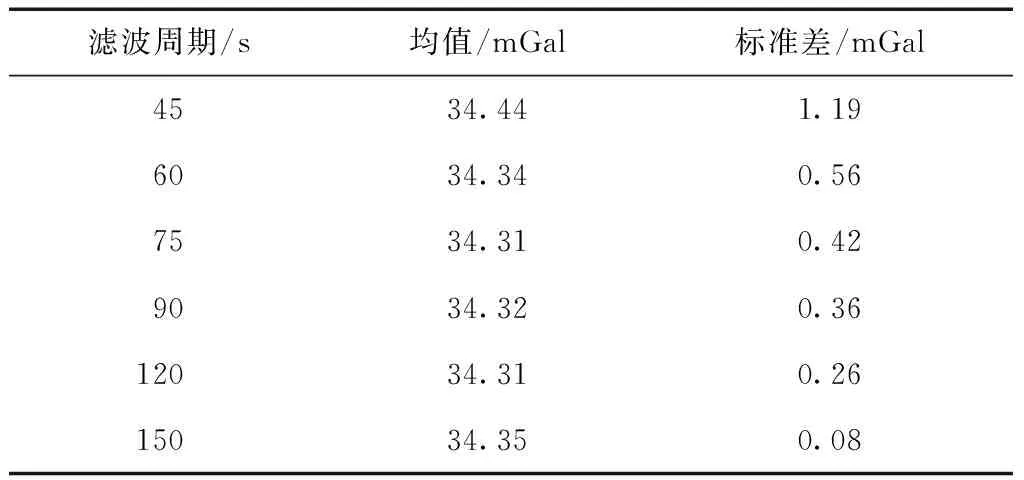
表6 转台周期240 s时加速度(真值为34.27 mGal)

在45 s的滤波周期条件下，加速度测量标准差小于1.5 mGal，平均值偏差小于0.3 mGal；60 s的滤波周期条件下，加速度测量标准差小于1 mGal，平均值偏差小于0.1 mGal；75 s滤波周期下，加速度测量标准差小于0.6 mGal，平均值偏差小于0.1 mGal；90 s滤波周期下，加速度测量标准差小于0.5 mGal，平均值偏差小于0.1 mGal；120 s滤波周期下，加速度测量标准差小于0.25 mGal，平均值偏差小于0.1 mGal；150 s滤波周期下，加速度测量标准差小于0.1 mGal，平均值偏差小于0.1 mGal。GPS载波相位测量加速度方法得到的加速度均值与参考加速度之间的误差小于0.3 mGal，测量得到的加速度模偏大，可能是实际旋转半径大于理论旋转半径。加速度测量值的标准差随着滤波周期的增大而减小，滤波周期大于60 s时，标准差低于1 mGal。4组实验的加速度测量精度十分接近，说明对于频率范围在0.004～0.006 Hz的加速度信号，该方法能够实现有效测量。

3 结束语

本文实现了基于DGPS载波相位计算运动载体加速度的方法，并设计转台实验对该方法的精度进行评估。利用转台旋转时所产生的向心加速度作为参考基准，评估测量得到的加速度的模的精度。4组转台实验结果表明，滤波周期大于60 s时，加速度的模的标准差小于1 mGal，并且标准差随着滤波周期的增大而降低。DGPS载波相位测量加速度的方法能够满足1 mGal的航空重力测量要求。调整GPS天线使其保持水平，以测出东北天3方向的加速度测量精度是下一步需要解决的问题。

[1] KENNEDY S L.Acceleration estimation from GPS carrier phases for airborne gravimetry[D].Calgary：The University of Calgary，2002.

[2] BRUTON A M，GLENNIE C L，SCHWARZ K P.Differentiation for high-precision GPS velocity and acceleration determination[J].GPS solutions，1999，2(4)：7-21.

[3] BRUTON A M，SCHWARZ K P.Deriving acceleration from DGPS：toward higher resolution applications of airborne gravimetry[J].GPS Solutions，2002，5(3)：l-14.

[4] BROZENA J M，MADER G L，PETERS M F.Interferometric global positioning aystem：three-dimensional positioning source for airborne gravimetry[J].Journal of GeoPhysical Research，1989，94(B9)：12153-12162.

[5] KWON J H，JEKELI C.A new approach for airborne vector gravimetry using GPS/INS[J].Journal of Geodesy，2001，74：690-700

[6] JEKELI C，GARCIA R.GPS phase accelerations for moving-base vector gravimetry[J].J Geodesy，1997，71(10)：630-639.

[7] SALAZER D，HERNANDEZ P M，JUAN J，et al.GNSS data management and processing with the GPSTk[J].GPS Solutions，2010，14(3)：293-299.

[8] 张开东.基于SINS/DGPS的航空重力量方法研究[D].长沙：国防科学技术大学，2007.

[9] 彭秀英.GPS周跳探测与修复的算法研究与实现[D].青岛：中国石油大学，2007.

[10] 肖云，夏哲仁.航空重力测量中载体运动加速度的确定[J].地球物理学报，2003，46(1)：62-67.

[11] 孙中苗，石磐，夏哲仁.利用GPS和数字滤波技术确定航空重力测量中的垂直加速度[J].测绘学报，2004，33(2)：111-115.