一种PCB动态应变的监测方法研究

杨龙,贺青川,陈文华,潘骏,朱谦

（浙江理工大学浙江省机电产品可靠性技术研究重点实验室,杭州 310018）

0 引言

机电设备在工作过程中，印刷电路板（Printed Circuit Board,PCB）受振动载荷作用时，产生的弯矩与固定于PCB上元器件的惯性力共同作用会使PCB基体、元器件、引脚和焊接点产生过大的应力和应变，导致PCB分层、焊点断裂、焊点脱落、引脚断裂、元件的封装开裂等失效模式发生，任何一种失效模式发生都可能导致机电设备故障[1-3]。因此，研究建立在线监测机电设备中PCB受振动作用时的振幅、应力、应变方法，能够为实现对PCB分层、焊点断裂、焊点脱落等失效模式进行预测、保障设备正常运行提供技术支撑[4-6]。

目前，获得PCB受冲击和振动载荷时的动态响应参数的技术途径主要有两种：一是通过实验测量，可以获得PCB在不同振动载荷下的动态响应参数[7-8]；二是结合有限元计算软件，通过数值计算，获得PCB动态响应参数，所用方法包括质量平均法、质量与刚度平均法、局部平均法等[9-10]。针对数值计算方法，关键是如何获得准确可靠的输入参数（弹性模量、泊松比、刚度、阻尼、有限元模型的边界条件等）来提高计算结果的准确性[11-12]。另外，关于如何建立PCB动态应变的理论计算方法，快速获得PCB在不同载荷下动态响应的研究也从未间断[13]。通过理论计算的PCB动态响应参数和应变，可作为分析实验测量结果和数值模拟计算结果准确性的参考。然而，利用上述技术途径均无法实现对PCB动态应变的长期实时监测。

在上述背景下，本文根据Timoshenko薄板应变计算模型[14]，推导出了PCB振动速度与动态应变的数学关系，提出了一种PCB动态应变监测的方法。在此基础上，结合实验，通过对比分析实测与理论计算PCB应变，验证本文提出的应变监测方法的可行性，为PCB分层、焊点断裂、焊点脱落等失效预测奠定技术基础。

1 PCB应变计算方法

PCB由多层环氧树脂薄板碾压合成，中间具有导电金属层，因此其材料属性会随载荷方向的变化而变化[10-12]。又因PCB具体的层叠方向未知，目前在确定PCB的材料属性时，通常按照各向同性材料处理，且假设PCB的厚度均匀、各层的材料属性相同。

1.1 应变计算基本方程

当PCB受弯曲应力和面内应力同时作用时，其动能方程和应变能方程表达式为[15]：

式中：a和b为x和y方向长度（坐标系如图1所示）；A=ab为PCB面积；m为PCB面密度；h为厚度；E为弹性模量；μ是泊松比；D=Eh3/[12（1-μ）]是刚度；w=w（x,y,t）是挠度函数；φ=φ（x,y,t）是应力（Airy）函数。式（2）中第一项是由弯曲应力推导出，第二项由面内应力推导出。

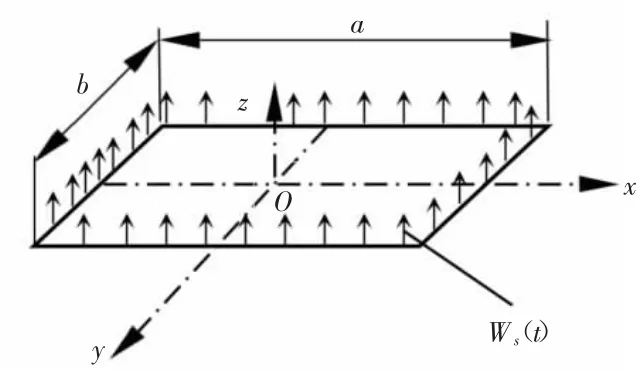
图1 PCB模型

为便于表述，引入拉普拉斯算子Δ和L算子：

函数w和φ的表达式如下：

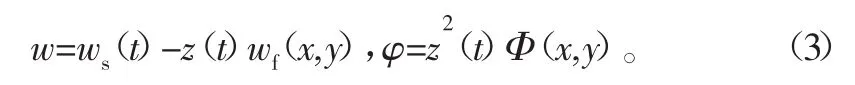
式中：ws（t）为固定的支撑架坐标；wf（t）为模态的挠度函数；z（t）为主坐标；Φ（x,y）为静应力函数；函数φ为

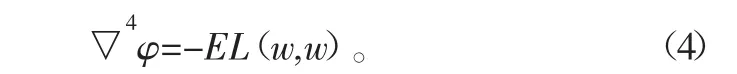
当边界条件为固支时，边界位移为0，因此可满足

对于固支条件（1≤a/b≤1.5），wfc（t）为[15]

将式（3）和式（6）代入式（4）,得：

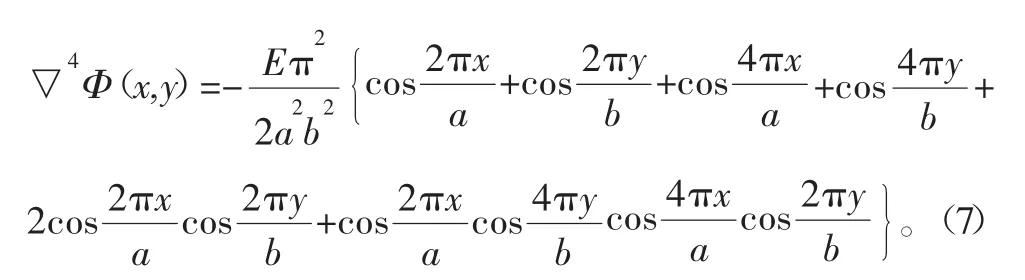
求解式（7），得固支PCB的静应力函数Φ（x,y）为

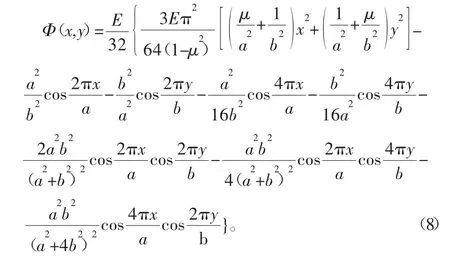
1.2 动态响应参数计算

将式（3）挠度函数代入式（1）和式（2），得：

式中：

式中：M0为与激振力相关的归一化质量；M为与系统自身振动相关的归一化质量；ω0为自然频率；α为非线性参数。

将式（11）和式（12）代入Lagrange方程，得：

得到Duffing型非线性微分方程：

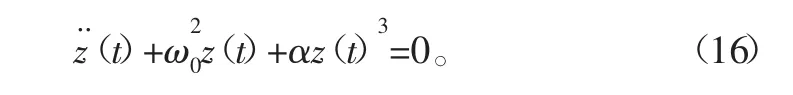
根据椭圆函数解的特征，式（16）的通解如下：

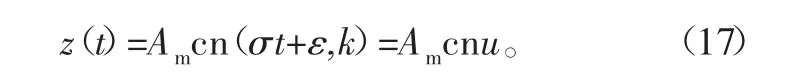
式中：σ为频率参数；t为时间；ε为初始相位角；A为振幅；k为椭圆函数的模数。

对式（17）微分，可得：

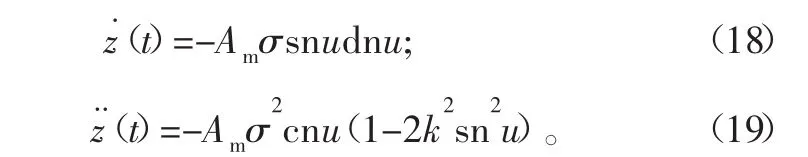
将式（17）和式（19）代入式（16）,可验证式（17）满足方程解的要求。当t=0时，振动初始作用于ws（t），可认为位移z（t）没有变化，而速度z˙（t）为最大值，因此主坐标可满足下列关系：

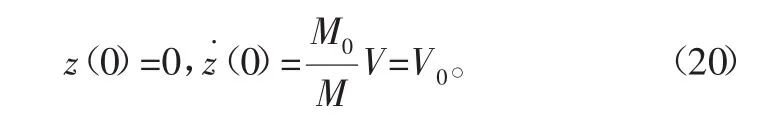
式中，V为ws（t）初始速度。将式（17）和式（18）代入式（20），可得：

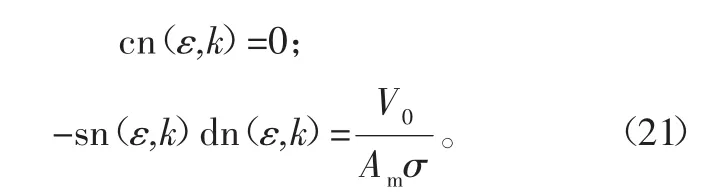
由式（21）中第一式可得：

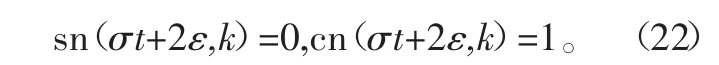
因此，可求得相角

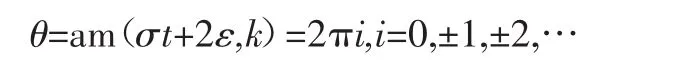
即：

式中K（k）是完全椭圆积分。初始相位角ε为：

由式（21）中第二式可得：

其中：

将式（21）代入式（25），可求得：

其中

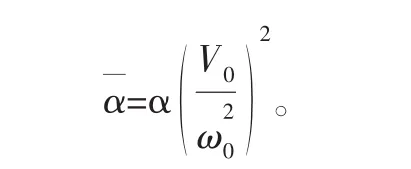
若把式（16）还可以改写为下面的形式：

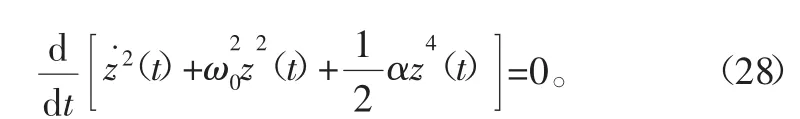
即

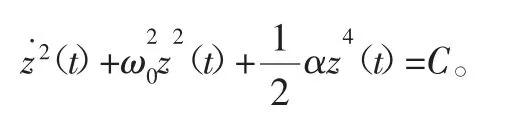
当PCB初始位移、速度为0，则常数C也为0，因此

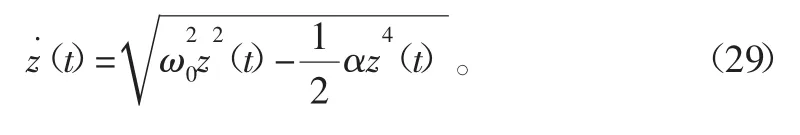
式（23）为时间的函数表达式，因此又可改写为

其中

式（31）为模数为k的第一类椭圆积分。当z（t）在第一个1/4周期达到最大值zma（xt）时，相角θ取得最大值。此时，式（35）变为模数为k的第一类完全椭圆积分：

再由式（27）可得：

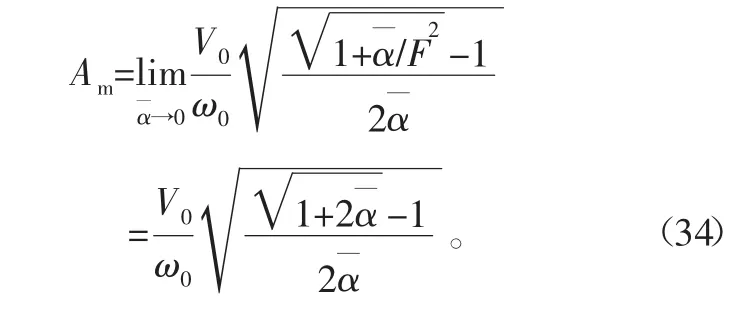
1.3 应力与应变计算

PCB的动态应力可利用下列关系式进行计算[14-15]：

根据式（35），可得应力计算公式如下：

PCB的动态应变可以根据广义虎克定律进行计算：

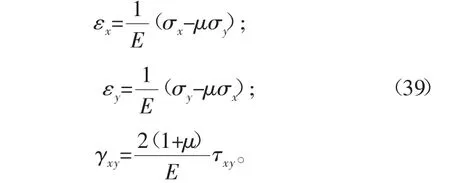
2 应变测量实验

实验用的PCB板及螺栓孔所在位置尺寸参数如图2所示：其中PCB板长为230 mm，宽为152 mm；螺栓孔所在位置a=220 mm，b=142 mm；PCB板厚h=2 mm，PCB板质量M=0.141 kg；弹性模量E=210 GPa，泊松比μ=0.21。测量应变所用设备如图3所示，应变测量使用三轴应变片（0°/45°/90°），应变片1～5位置如图2所示。应变片0°对应x方向，所测应变用S_X表示；90°对应y方向，所测应变用S_Y表示；45°对应与x、y方向夹角为45°，所测应变用S_XY表示。

图2 PCB几何模型

由文献[3]～[6]可知，采用螺钉固定PCB可近似固支条件，因此本文用8个M3螺钉，按照如图2所示的位置固定。实验装置如图3所示，激振源为电磁振动台，加载方式为恒速正弦扫频振动：速度为20 mm/s；扫频范围分为10～300 Hz；线性扫频速度300 Hz/min。实验过程中，采用KEYENCE公司的LK-G5000激光速度传感器测量振动速度。实验过程中，应变和速度传感器的采样率设置为1.5 k。在测量应变测量前，用一块与图2所示几何参数相同的PCB进行共振频率测试，结果如图4所示，一阶共振频率约为250.5 Hz。由此可以确定，将扫频范围定为10～300 Hz，能够测得共振频率处应变。

图3 实验照片

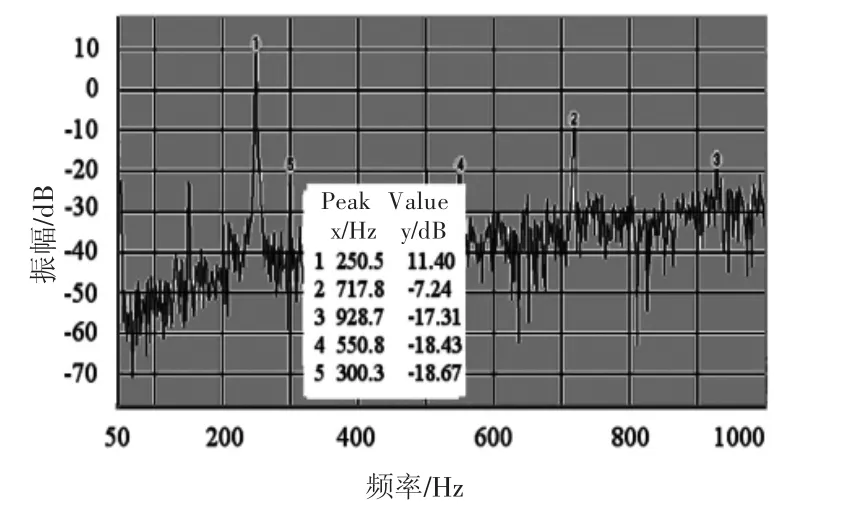
图4 共振频率测试结果

根据实验条件，因正弦扫频速度为5 Hz/s，记录数据量为1.5k，据此可知数据记录速度为0.3 k/Hz。数据采集的起止时间由软件自动记录，由此可将得到关于时间序列的应变数据转换为与频率对应的序列。图5为测得的5个位置的结果。图6为1号位置（如图2所示）的测量结果。图7为1号位置的运动速度。由图6和图7可以看出，共振频率位置的应变和速度均达到峰值。

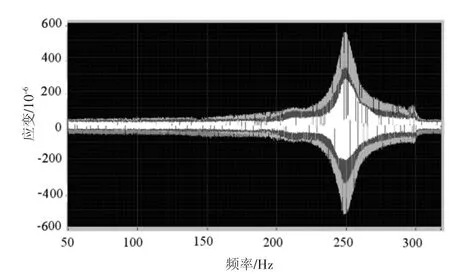
图5 5个位置的应变测量结果

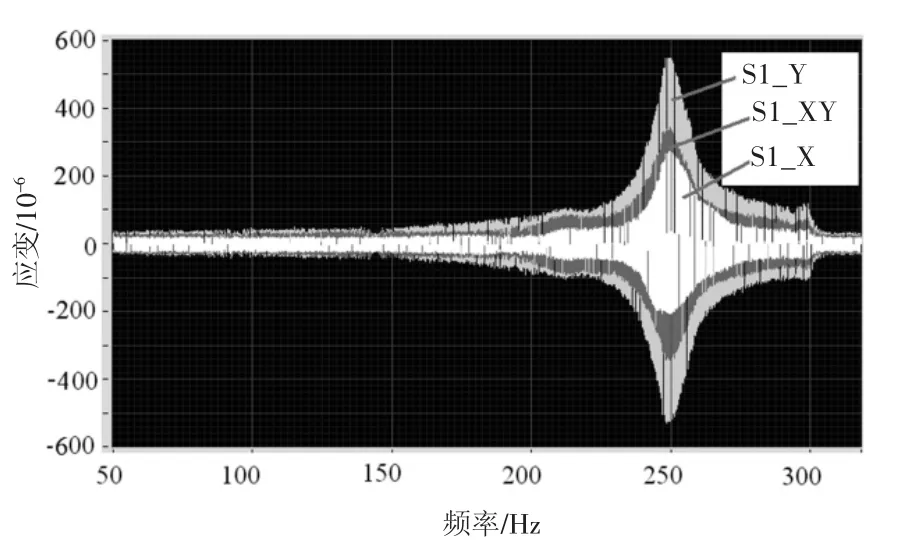
图6 1号位置的应变测量结果

图7 1号位置的速度

3 应变计算与分析

依据第1部分给出的动态应变计算方法，以1号位置（如图2所示）应变计算为例，进行应变计算，计算过程步骤如下：

1）面积：A=a×b=220×142=31 240 mm2；

2）面密度：m=M/（A×g）=M/（A×9800）=4.606×10-10kg·s2/mm3;

3）振动频率：依据式（13）得ω=2453.05 Hz；

4）振动速度:恒速V=20 mm/s;

5）弹性刚度:D=Eh3/［12（1-μ）］=1494.5 kg·mm;

6）非线性参数（式（15））：α=421 306.73 mm-2·s-2;

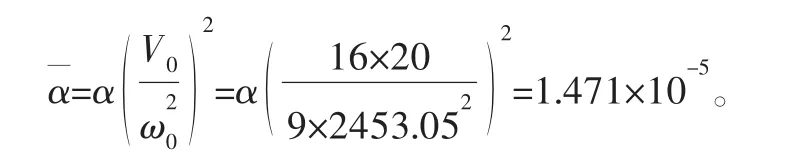
7）振幅（依据式（34））:

8） 应力（依据式（35）～（38）：σx=0.02 kg·mm－2;σy=0.023 47 kg·mm－2;τxy=0。

9）应变（式（39））：

重复上述计算过程，以2453.05 Hz为振动频率ω输入参数，以测量的速度（图7）为速度输入参数，其它参数不变，计算1号位置（x=y=0）处的应变，结果如图8和图9所示。从图中可以直接看出：计算所得应变大于图6所示测量所得应变。表1给出了测量和计算结果的峰值及相对偏差。从表1中可以看出，相对误差不超过10%。

图8 计算所得应变S1_X

图9 计算所得应变S1_Y

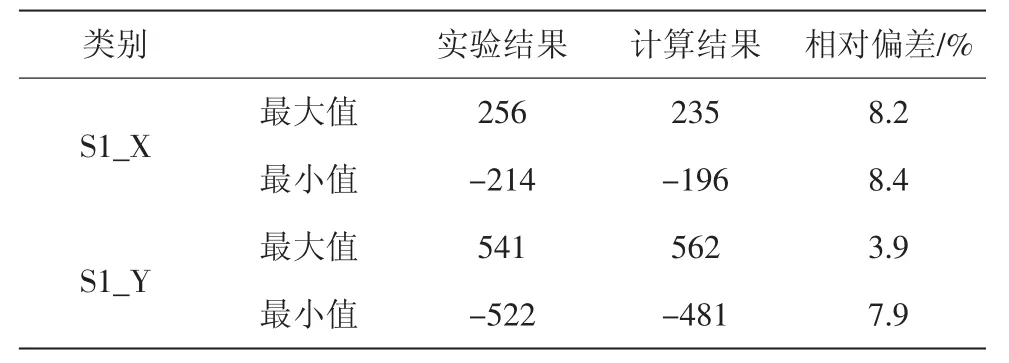
表1 测量和计算结果的峰值及相对偏差 10-6

引起偏差的原因主要有两方面:一是受测量误差影响，应变片本身靠敏感栅来感应PCB表面的应变，而敏感栅具有一定尺寸，故所测量应变实际是敏感栅所覆盖的一块小面积上应变量的均值;另外，粘贴应变片也是人为引入误差因素的一个实验环节。粘贴应变片时，要求应变片与测量物体表面无缝粘贴，且胶水层应尽量薄。然而实验时，应变片的粘贴层中可能会夹有气泡，或粘贴固化不均，这些因素都将导致测量结果与真实值之间存在偏差。二是受输入的材料参数误差的影响，主要包括弹性模量、泊松比。在推导PCB振动速度与动态应变的计算公式时，假设PCB各向同性材料，PCB各层的厚度均匀、各层的材料结构均匀。然而，这些假设会与实际存在偏差，从而造成计算结果与实测结果出现偏差。

总体而言，X、Y方向的应变计算结果与实测结果的相对偏差在工程允许的15%以内。由此可知，若要在线监测PCB应变，可以在被监测位置放置微型速度传感器，并利用该传感器监测振动速度；然后以监测的速度作为输入参数，利用本文给出方法计算应变。由于速度是实时监测的，因此计算出的应变能够反映PCB应变的动态变化过程。另外，理论计算不足之处在于45°方向的应变S_XY无法通过计算获得。

4 结论

本文根据Timoshenko薄板应变计算模型，推导出PCB振动速度与动态应变的数学关系，提出了一种PCB动态应变监测的方法。首先，通过在PCB上放置传感器，监测振动速度；然后以监测的速度信号作为输入参数，利用本文推导的应变计算方法计算出应变，从而实现对PCB应变动态变化过程的监测。通过对比分析实测数据与理论计算结果，验证了利用本文方法可实现对PCB应变动态变化的监测；为PCB分层、焊点断裂、焊点脱落等失效预测提供了技术支撑。

[1] VEGA A,MONAGAS J,CEREZO J M,et al.Edge connector for mechanical and electrical interconnection of PCBs[C]//IECON.IEEE,vol.3.2002:1948-1953.

[2] POMMERENKE D, MAHESHWARI P. Soft Failure Mechanisms and PCB Design Measures[M].System Level ESD Co-Design,2016.

[3] BALAMURUGANS,ANANDP,JAYARAMANS,etal.Vibration analysis on printed circuit board using finite element model[C]//International conference on Recent Advancements In Design,Automation and Intelligent Systems.2016.

[4] YANG Y.Failure analysis for poor solderability of Au surface of PCB [C]//International Conference on Electronic Packaging Technology.2015:1444-1447.

[5] MA Chuan.Fault Diagnosis and Maintenance Analysis of Mechanical and Electrical Equipment in Mine [J].Modern Manufacturing Technology and Equipment,2016(9).

[6] BI Z M,JR MUELLER D W.Finite element analysis for diagnosis of fatigue failure of composite materials in product development [J]. International Journal of Advanced Manufacturing Technology,2016,87(5-8):1-13.

[7] CHEN Y S,WANG C S,YANG Y J.Combining vibration test with finite element analysis for the fatigue[J].Microelectronics Reliability,2008,48(4):638-644.

[8] YU D,KWAK J B,PARK S,et al.Dynamic respo nses of PCB under product-level free drop impact[J].Microelectronics Reliability 2010,50(7):1028-1038.

[9] SINKOVICS B,KRAMMER O.Board level investigation of BGA solder joint deformation strength[J].Microelectronics Reliability,2009,49(6):573-578.

[10]RENG,LIB,LID,etal.ModalAnalysisofthePrintedCircuitBoard Based on Finite Element Method[C]//International Conference on ComputerScienceandElectronicTechnology.2015.

[11]SUHIR E,GHAFFARIAN R.Board level drop test:exact solution to the problem of the nonlinear dynamic response of a PCB to the drop impact[J].Journal of Materials Science:Materials in Electronics,2016,27(9):1-8.

[12]VRIES J D,BALEMANS W,VAN DRIEL W D.Predictive modeling of board level shock-impact reliability of the HVQFN-family[J].Microelectronics Reliability,2010,50(2):228-234.

[13]SUHIR E，GHAFFARIAN R.Board level drop test:exact solution to the problem of the nonlinear dynamic response of a PCB to the drop impact[J].Journal of Materials Science:Materials in Electronics,2016,27(9):1-8.

[14]SUHIR E,VUJOSEVIC M,REINIKAINEN T.Nonlinear dynamic response of a'flexible-and-heavy'printed circuit board(PCB)to an impact load applied to its support contour[J].Journal of Physics D:Applied Physics,2009,42(4):1-10.

[15]SUHIR E,STEINBERG D S,YU T X.18.Dynamic Response of PCB Structures to Shock Loading in Reliability Tests[M]//Structural Dynamics of Electronic and Photonic Systems.John Wiley&Sons,Inc,2011:415-434.