单圆柱滚子包络蜗杆传动啮合效率分析

2018-03-05王小林韩志段冬冬

机械工程师 2018年2期

王小林，韩志，段冬冬

（河南理工大学机械与动力工程学院，河南焦作 454000）

0 引言

滚柱包络环面蜗杆传动原理是将传统环面蜗杆副中的蜗轮轮齿以回转体（本文中以单圆柱滚子为例）代替，以期达到用滚动摩擦替代滑动摩擦，提高蜗杆副啮合效率的目的[1]。其具有承载能力强、运动平稳、使用寿命长等特点，尤其是具有较高的传动效率，使其显著地区别于传统的蜗杆传动。

经过样机试制与试验，发现试验中蜗杆副的啮合效率与理论计算数值有较大差距[2-4]，不能够充分发挥这种型式传动啮合效率高的优点。因此有必要对滚柱蜗杆传动的啮合效率进行理论研究。影响啮合效率的因素有很多，包括理论分析中存在的偏差和实际应用中存在的误差[5-6]。滚柱蜗杆副传动实现了回转体和蜗杆齿面接触，改变了接触型式，但在沿着回转体轴线方向存在蜗杆副的相对运动速度分量[7]，接触齿面间滑动摩擦和滚动摩擦情况复杂，增加了构建蜗杆副啮合效率公式模型的难度。

本文以单圆柱滚子包络环面蜗杆传动为研究对象，利用蜗杆与蜗轮之间作用力和反作用力的关系，建立了啮合效率公式，以此为基础分析了摩擦因数、传动比和滚柱半径对蜗杆传动啮合效率的影响，为滚柱包络环面蜗杆传动的理论设计和结构优化提供了重要的参照。

1 滚柱受力分析

单圆柱滚子包络环面蜗杆副运动的实现，是以蜗杆作为运动的输入部件，通过蜗杆齿面和滚柱外表面接触，带动滚柱转动，最终使蜗轮按照确定的传动比运动[8-10]，如图1所示。以滚柱外表面上的任一接触点P0为研究对象进行受力分析，如图2所示，坐标系及活动标架以文献［11］中的设置为参考。

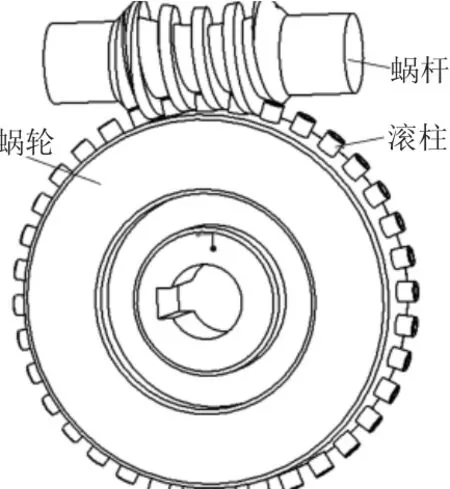
图1 传动原理

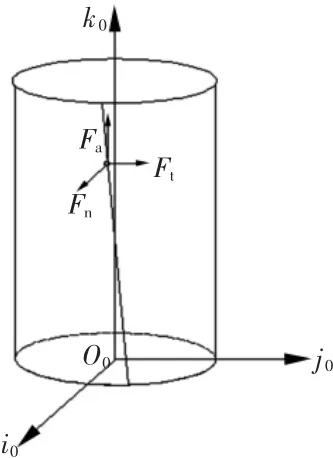
图2 滚柱受力分析

图2中：P0是接触线上任意一个接触点；Ft是接触点在滚柱周向方向受到的滑动摩擦力；Fa是接触点在滚柱轴向方向受到的滑动摩擦力；Fn是接触点在滚柱法向方向受到的滑动摩擦力。

蜗杆与蜗轮的相对速度在环面蜗杆副的切平面内，在接触点处的滚柱法向没有分速度，所以Fa和Fτ都位于接触点处的切平面内[12-13]。

滚柱在周向滑动摩擦力Ft的作用下，绕着轴线z2以角速度ω2转动，故忽略其对效率计算的影响[14]。取滚柱作为研究对象，滚柱受到蜗杆作用的正压力Fn和滑动摩擦力Ff，二者的矢量和就是接触点受到的合力，将合力设为Fr2，Fr2=Fn+Ff；取蜗杆作为研究对象，蜗杆受到滚柱作用的正压力Fn′和滑动摩擦力Ff′，二者的矢量和就是蜗杆受到滚柱的合力，将合力设为Fd1′，Fd1′=Fn′+Ff′。根据作用力和反作用力的关系，其中Fn=-Fn′，Ff=-Ff′。蜗杆受到的驱动力应与滚柱施加在蜗杆上的合力Fd1′大小相等，方向相反，设为Fd1：

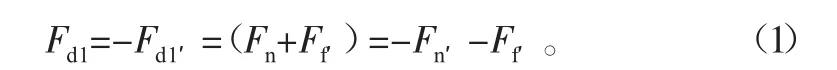
式中，Fd1是施加在蜗杆上面的驱动力。

2 啮合效率公式

根据机械原理知识[15]可得，机械效率按照瞬时输出功率和瞬时输入功率比值来计算。

设蜗轮输出效率为Pr，计算公式如下：

设蜗杆输入功率为Pd，计算公式如下：

由蜗杆输入功率Pd和蜗轮输出功率Pr可得，滚柱包络环面蜗杆传动的理论啮合效率η的表达式如下：

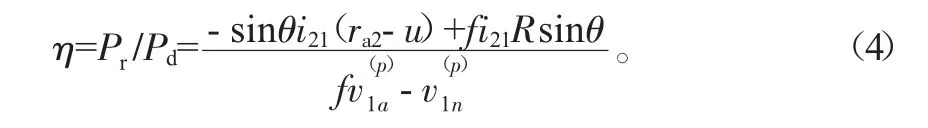
3 啮合效率影响参数

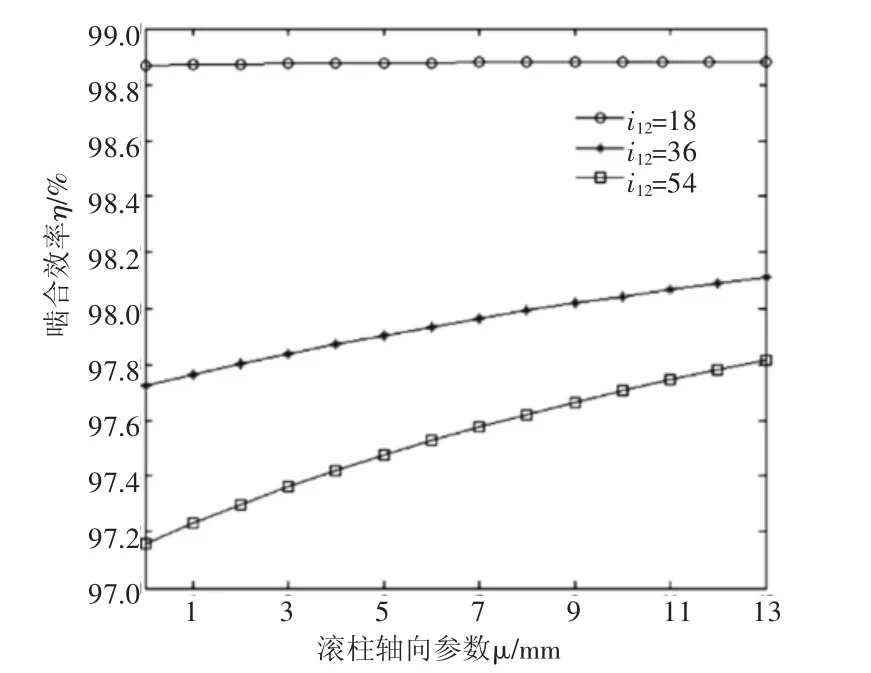
图3 η与i12的关系

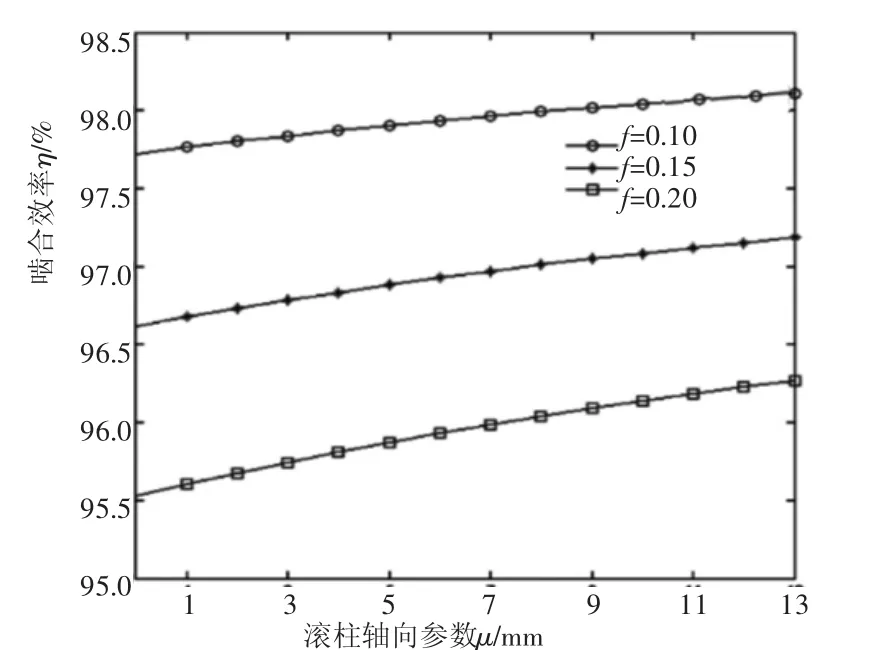
图4 η与f的关系

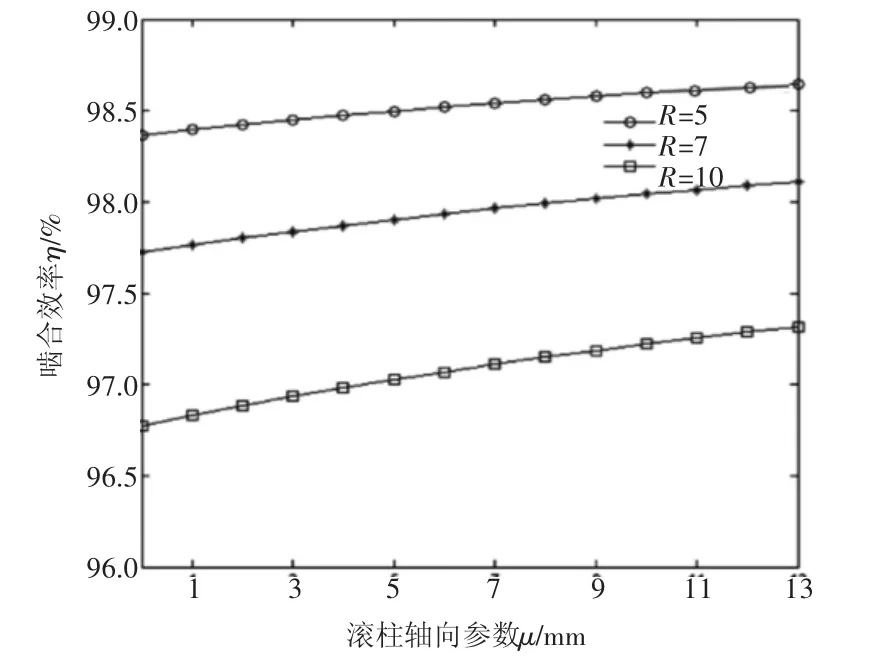
图5 η与R的关系

由啮合效率公式（4）可以看出，与啮合效率有关的参数有：θ、i21、ra2、u、f、R、φ1、a。其中，ra2为滚柱齿顶所在圆半径，a为中心距，两者在蜗杆副运动规律确定时即为定值。当蜗轮转角φ2=-25°时，以滚柱齿面上的接触线为研究对象，在MATLAB中利用单一变量法作图，它上面的啮合效率η和传动比i21、摩擦因数f、滚柱半径R的关系分别如图3～图5所示。

综合比较图3～图5发现：在滚柱轴向参数u一定时，减小传动比i12、降低摩擦因数f、减少滚柱半径尺寸R，会使啮合效率升高，反之，啮合效率下降；从滚柱柱顶到底部，啮合效率逐渐增大，滚柱表面上啮合效率分布不均匀。

对比图3～图5也可以看出，影响啮合效率的参数中，摩擦因数所占比例最大，其次是传动比，滚柱半径值影响较小。当f增大0.05时，η降低幅度超过2%。因此，应保持环面蜗杆副接触区处于良好的润滑状态，选择合适的润滑条件和润滑方法，避免边界润滑和干摩擦的出现。

对于滚柱上轴向参数u=0的位置，当蜗轮转角φ2在范围-25°～25°内变化时，啮合效率φ和传动比i21、摩擦因数f、滚柱半径R的关系分别如图6～图8所示。

图6～图8表明：啮合效率变化以蜗轮转角φ2=0为节点，在该点左侧时，啮合效率随着蜗轮转角增大而减小，在该节点右侧时，啮合效率随着蜗轮转角的增大而增大；在同一蜗轮转角处，增大传动比i12、升高摩擦因数f、增加滚柱半径R，啮合效率η减小。

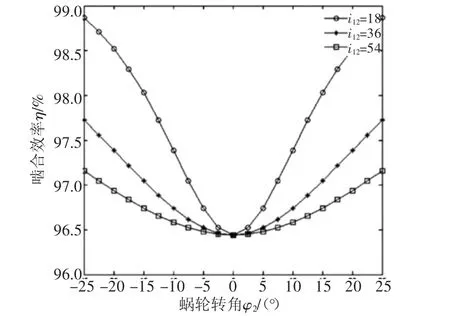
图6 η与i12的关系

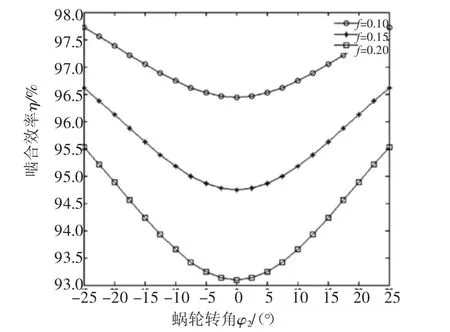
图7 η与f的关系

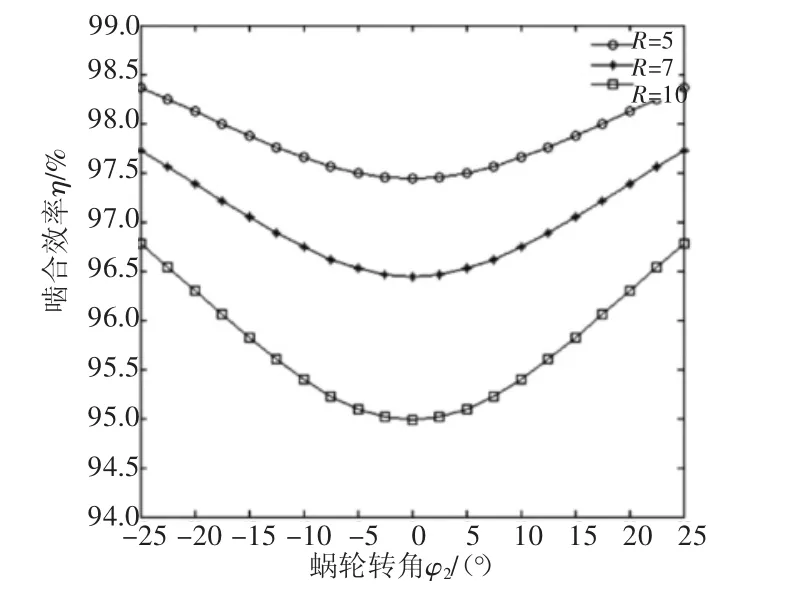
图8 η与R的关系

由图8得到结论：在滚柱半径R=10 mm时，啮合效率降低幅度已经很大，当蜗轮滚柱运动到蜗杆喉部位置时，啮合效率与滚柱半径R=5 mm时相比，已经降低了大约3%，因此在满足传动所要满足的强度和刚度条件下，滚柱半径值不宜过大。

上面是在蜗轮转角φ2处于-25°～25°范围内进行分析的，实际的生产要求蜗杆与蜗轮运动的转角范围比这个大许多。当滚柱与蜗杆连续啮合传动时，选取滚柱柱顶位置，啮合效率η与摩擦因数f、传动比i12和滚柱半径R之间的关系分别如图9～图11所示。

由图9、图11可知，摩擦因数f和滚柱半径R对啮合效率η的作用效果相似，只能等比例放大或者缩小啮合曲线图，不会改变曲线的形状，即在蜗轮某个确定转角时，较小的摩擦因数f和较小的滚柱半径R总是对应于较高的啮合效率。

由图10可知，在蜗轮转动一周的范围内，传动比i12=36时的啮合效率曲线和i12=18时的啮合效率曲线有4个交叉点，对应的横坐标φ2依次是φ2=0°、120°、240°和360°。

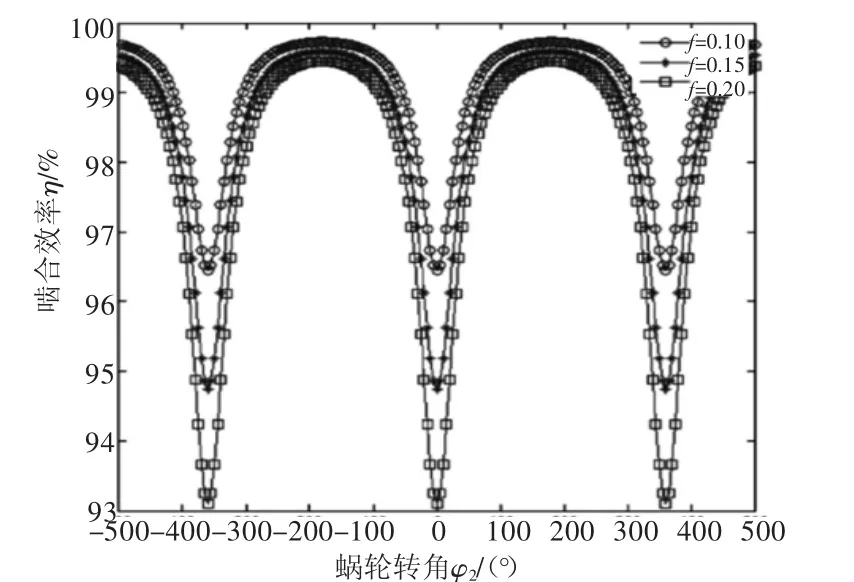
图9 η与f的关系

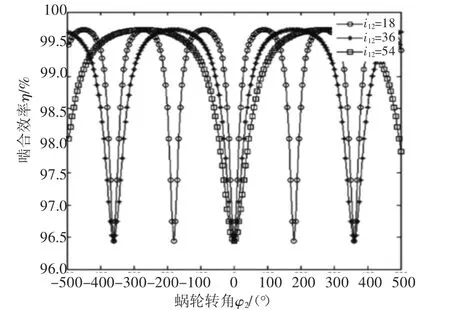
图10 η与i12的关系

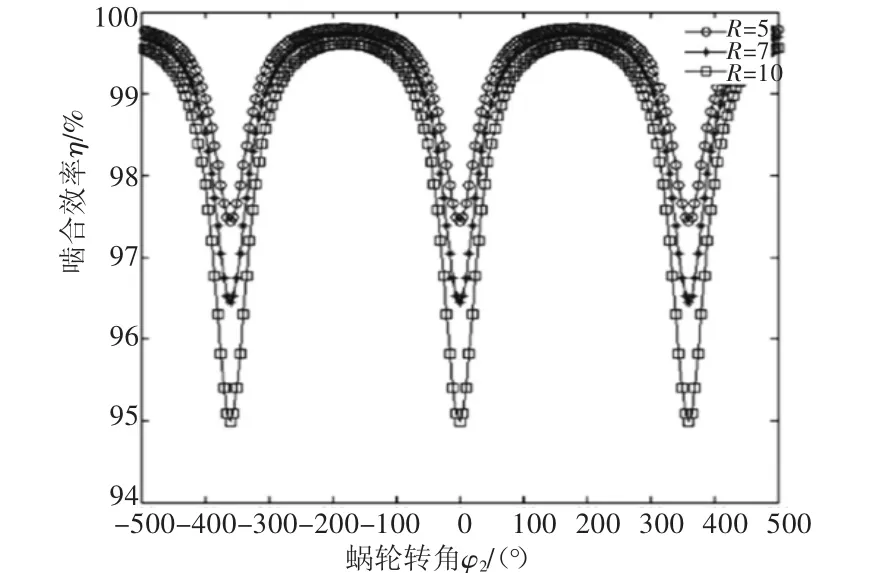
图11 η与R的关系

在φ2=0°～120°和120°～360°范围内，i12=18时的啮合效率高于i12=36时的啮合效率；当φ2=120°～240°时，i12=18时的啮合效率低于i12=36时的啮合效率。对于其他曲线之间的啮合效率对比，由于啮合效率随着蜗轮转速的变化曲线成“圆拱形”，所以有着类似的结论，只是啮合效率相等点的横坐标发生变化，即对应于不同的蜗轮转角。

所以，比较蜗杆副啮合效率高低时，在其他参数条件相同的情况下，对应于不同的传动比大小，由于在不同的蜗轮转角时刻，啮合效率之间大小关系会发生变化，不能简单地说某个传动比数值时啮合效率比另一个数值大，应当算出在确定的蜗轮运动周期内，啮合效率在这个周期内效率和的大小，再比较对应不同传动比时的啮合效率。

4 结论

1）滚柱齿面上的啮合效率分布不均匀，在滚柱底部的位置时的啮合效率大于在滚柱柱顶的啮合效率，从滚柱柱顶到滚柱根部，啮合效率单调递增。2）摩擦因数对啮合效率的作用最大，其次是传动比，滚柱对啮合效率的影响效果较小，但需要保证滚柱具有足够的强度和刚度，以传递蜗杆副传动的运动和力。3）摩擦因数和滚柱半径的变化改变啮合效率曲线的纵向形状，传动比的变化使其横向形状改变，啮合效率呈周期性变化。

[1] 边辉.对滚柱包络环面蜗杆传动机构的一点思考[J].机械工程师,2010(10):136-137.

[2] 杨玉虎,沈煜,张策,等.环面蜗杆类零件实体建模研究[J].天津大学学报(自然科学与工程技术版),2004,37(6):471-474.

[3] 刘新华.无侧隙双滚柱包络环面蜗杆传动减速器的设计与分析[D].成都:西华大学,2010.

[4] 陈尚友.无侧隙滚柱包络端面啮合蜗杆传动建模与研究[D].成都:西华大学,2015.

[5] 张宝锋,崔亚辉,刘凯,等.渐开线圆柱直齿轮结构参数对啮合效率的影响分析[J].机械强度,2015,37(1):122-127.

[6] 许立忠,闻岩.滚锥包络环面蜗杆传动效率研究[J].润滑与密封,2001(4):10-12.

[7] 沈煜,杨玉琥,杨一平.滚柱包络环面蜗杆传动的运动学分析[J].机械设计,2003,20(6):38-40.

[8] 王进戈,张光辉.滚锥包络环面蜗杆传动的理论研究与参数优化[J].重庆大学学报,1992,15(2):58-64.

[9] 王其超,刘健.滚动式回转面包络点啮合环面蜗杆传动的点啮合原理[J].大连工业大学学报,2000(4):281-285.

[10] 张永强.无侧隙双滚柱包络环面蜗杆传动的几何特性及研究[D].成都:西华大学,2014.

[11]洪雷.无侧隙双滚子包络环面蜗杆传动的理论研究[D].成都:西华大学,2008.

[12] 柳在鑫,王进戈,张均富,等.交错轴双滚子包络环面蜗杆传动啮合分析[J].四川大学学报(工程科学版),2012,44(4):221-225.