基于实测数据的行人上下楼梯人体动力学模型

朱前坤， 陈 凯， 杜永峰， 李宏男, 刘路路

(1.兰州理工大学 防震减灾研究所，兰州 730050；2.大连理工大学 建设工程学部，辽宁 大连 116024；3.东南大学 土木工程学院，南京 210096 )

对于承载人群活动的人行天桥、楼板或者楼梯等结构而言，在正常使用时会产生不同程度的振动，人的活动是主要的激励作用，当人以接近结构基频的步频行走时产生的动力响应更大，因此人行走时的人致激励是模拟此类结构在人行走时的动力响应分析的关键。由于人行天桥和楼板与楼梯的结构形式的差异导致人在结构上行走时步态的差异，从而决定了人致激励模型的不同。学者们对楼板上的人行激励研究的比较多[1-3]，Bishop等[4-5]最早对楼梯上人行走时的落足曲线进行了系统的研究，得到了大量的不同频率下的动力荷载因子的统计值，并且得到了可供计算分析的荷载手册，之后又对荷载模型进行了系统的研究。Gaile等[6]对楼梯研究发现，当人们以正常速度或者最适合自己的速度上下楼梯时，步频趋近于定值，并且得到了上下楼梯前三阶的动力荷载因子及相位角。

以上研究都是得到人对楼梯结构产生的荷载，却并不能真实的代表人在楼梯上行走时对结构产生的作用，尤其是现在的结构越来越趋向于轻质大跨，当这种柔性结构上人群密度较大时，结构的动力特性会发生变化，进而改变结构的基频，而结构的振动也会影响行人的步态，即人-结构会发生动相互作用。Barker等[7]研究发现密集的人群会增加体系的阻尼、减小结构的响应。秦敬伟等[8-9]对静态人体-结构相互作用进行了研究，结果表明不同的姿态的人体对结构的动力特性有不同的影响，而后又基于双足步行模型研究人体-结构相互作用，研究表明对于柔度较大的人行天桥，人体-结构相互作用较大。Kim等[10]对行人在人行桥上行走时产生的动力效果进行了研究，每个行人等价为一个包含质量、刚度、阻尼的生物力学系统，对比分析了在人致激励和生物力学系统下结构响应的差异。但是所采用的生物力学系统的参数取自于ISO5982规范[11]，该参数适用于站着不动的人，并不能代表行走的人，因为人在行走时膝盖会弯曲，从而改变整个身体的刚度。Felipe等[12]对人行桥上人行走时的活动进行了研究，采用33个实验对象得到大量加速度时程数据，建立数学模型，最终得到了竖向人体动力学模型的质量、刚度和阻尼等3个参数随频率变化的表达式。Toso等[13]在Felipe的基础上，优化了前者的实验方法和数学模型的求解，建立优化的人体动力学模型，并将该模型应用到人行桥的有限元模型中进行数值模拟，与实验结果对比可知优化的模型与实验数据更加接近。

目前楼梯采用更加轻质大跨的新颖的结构形式，其舒适度问题越来越受到关注，而且国内外学者对于楼梯上人致激励已经有了研究，但是对楼梯上行人的人体动力学模型却鲜有研究，人在楼梯上行走与在人行天桥上行走时的步态差异较大，有必要研究楼梯上的人体动力学模型。本文基于行人上下楼梯大量的实测数据，建立人在楼梯上活动时单自由度人体动力学模型。

1 数学模型的建立

与文献[12]类似，本文采用一个单自由度动力系统模拟人体，该系统代表上下楼梯的行人，其集中代表在行走时竖直方向的运动，系统中的表观质量是将人体的质量集中到重心处，刚度代表人体下肢的机械阻抗，阻尼代表人体的能量耗散。

1.1 模型假设

人在楼梯上行走时，在竖直方向上的行为特点是膝盖会弯曲，人的重心与踏步板之间会有一个相对位移，而且随着膝盖周期性的弯曲和伸直，相对位移也会周期性的变化，即竖向的运动是由于重心的上下起伏引起，同时由于踏步板的作用，运动系统中的刚度k、阻尼c和表观质量m也会变化。基于上述思想，用基础代表踏步板，用一个单自由度模型代表人体，在基础上构建一个单自由度模型，基础的运动与人体重心的运动保持平衡，该模型如图1所示。

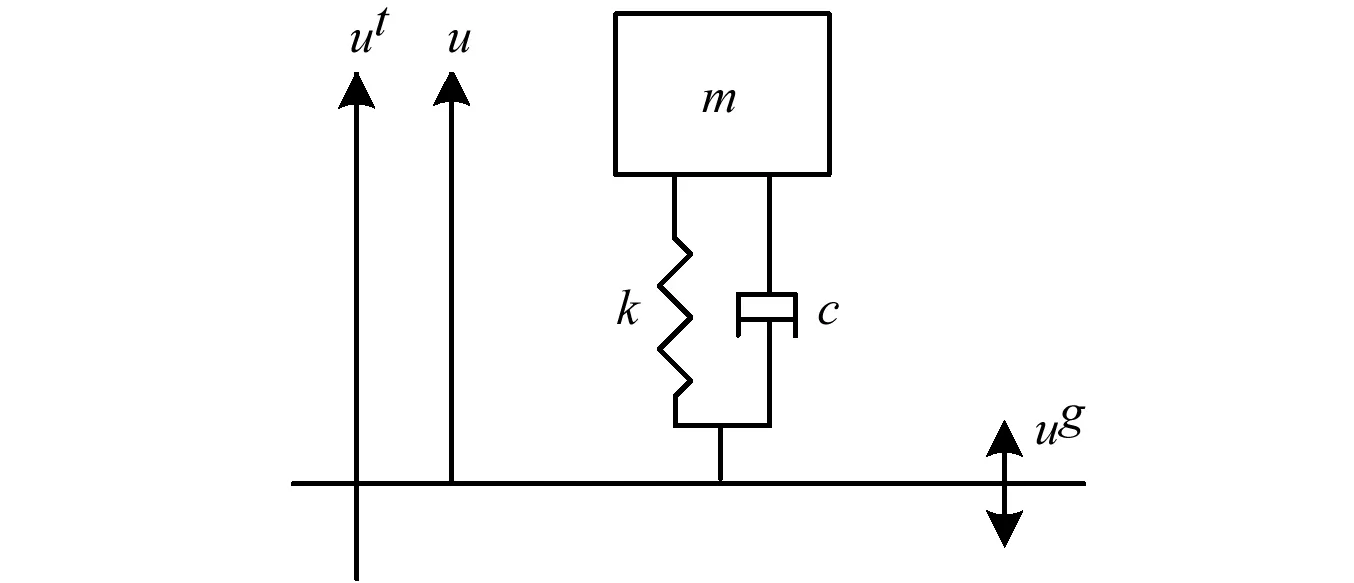
图1 在支撑作用下的单自由度模型Fig.1 SDOF under support

图1中，ut和u分别为该自由度关于固定参考点和基础的位移；ug为基础关于同样的固定参考点的相对位移。

实际情况是人体的重心在移动而不是基础，所以关键是基础和重心的相对运动。因此，该体系的平衡方程式为

(1)

由于该单自由度模型是连接到固定的基础上，两者之间作用力与反作用力相互平衡。假定踏步板的反作用力PGR等于质量块连接到踏步板之间产生的所有力的总和，表达式为

(2)

求解该微分方程，计算m，c，k。方程(2)的求解等价于求解如下位移频响函数：

(3)

式中：D(ω)为单自由度体系的稳态位移响应；PGR 0(ω)为激起该响应的谐波荷载幅值；ω为该谐波荷载的频率；j为复数。由方程(3)可得到该体系的加速度频响函数的方程式为

(4)

1.2 模型求解

式(4)中待求参数为m，c，k，也就是说需要三个方程联立求解，即确定加速度A(ω)和PGR 0(ω)的前三阶谐波幅值，产生一个3×3方程组，如方程(5)所示。

(5)

对于每个行人都可以测试得到一组加速度时程曲线，进行频谱分析，提取前三阶谱的幅值；而踏步板的反作用力PGR可以写成傅里叶级数的形式，在特定的频率下对应一个幅值，因此可以得到在前三阶加速度谱的频率下的谐波荷载值PGR 0(ω)。上楼梯和下楼梯的模型假设与求解过程类同，只是方程组中未知数的系数差异较大，导致上下楼梯的人体生物力学模型的不同。

2 试验测试

2.1 加速度的测量

本文采用新型微电子机械系统(MEMS)AH100B三轴加速度传感器测定行人上楼梯和下楼梯的加速度时程。在考虑不同楼梯的影响时，考虑其动力学特征的不同，其荷载模型参数不同，但仍可以将本文荷载模型作为参考使用。因为楼梯的不同对行人而言，最终影响的是行人上下楼梯时的步频，所以本文的实测试验数据主要考虑了行人上下楼梯时的步频大小，故在试验测试时，测试者将分别按照自己快、中、慢时的步速上下楼梯。如图2所示，试验是在某一教学楼的室外长悬挑楼梯上进行的，该楼梯是混凝土结构，悬挑长度1.3 m，水平倾角26°，共有10个梯段，每一梯段共有13个台阶。为了保证实验对象的多样性，减少实验误差，保证数据的可靠性，本文将针对不同年龄段的52个实验对象(31名男性和21名女性)进行测试，其基本信息如表1所示。

表1 测试者基本信息

试验测试时，将MEMS加速度传感器固定在人体质心部位，由文献[14]知：质心位置女性为0.55h；男性为0.57h(其中h为人体高度)。加速度传感器的采样频率设定为100 Hz。如图2所示，为保证信号的精确性，本次试验拟采用在每位测试者质心位置前面和背面固定两个相同的传感器，取两次信号的平均值作为一次试验获得的连续加速度时程。为了获得平稳的信号，要求每个测试者从平台开始走，一步走一个台阶，当踏上第2个台阶的时候开始采集数据，走完该梯段时终止采集。每个测试者将分别按照自己快、中、慢时的步速上下楼梯，上下楼梯时按照事先画好的直线走，测试者上下楼时将分别走12到18次，次数随机分配。同时要求每个测试者统一穿橡胶底的球鞋，被测试者为单独上下楼梯，考虑其个体效应。上楼梯和下楼梯各自测得了1 536组数据。

图2 某室外悬挑楼梯及测试者Fig.2 A cantilevered stair and test subject

2.2 确定

加速度的测量方法保证了信号的平稳，也就是说整个加速度时程避免了信号衰减的现象，信号的衰减会影响谱的幅值。限于篇幅的限值，此处随机选取一组上楼梯时竖向的加速度时程，如图3所示。通过离散傅里叶变换获得加速度时程的频谱图，如图3所示，每一组数据得到频谱图后都能够提取出前三阶的幅值(A1、A2、A3)和该幅值下对应的频率(ω1、ω2、ω3)。

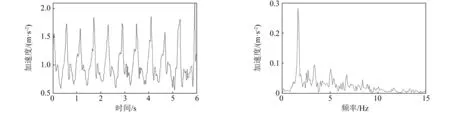
图3 加速度时程曲线及FFT频谱图Fig.3 Acceleration and time curve and FFT spectrum

2.3 确定PGR 0(ω)

在方程(5)中另外一个输入的参数为谐波荷载幅值PGR 0i(PGR 01、PGR 02、PGR 03)。人在楼梯结构上的行走对踏步板产生的激励可以写成傅里叶级数的形式，其中竖向的谐波激励形式如下：

(6)

式中：G为人体重量(N)；αzi为z向第i阶谐波的动载系数，也常称为动力荷载因子，定义为αi=Ai/G，Ai为第i阶谐波动荷载幅值；fp为人行走频率(Hz)；φzi为z向第i阶谐波相位角；n为模型中考虑的阶数。

本课题组对楼梯结构上竖向的人致激励研究成果如下[15]：

上楼梯时前3阶的动力荷载因子计算式为

(7)

下楼梯时前3阶的动力荷载因子的计算式为

(8)

在上述公式中fp=ωi/(2π)。

3 人体动力学模型参数分析

基于方程式(5)可知输入的参数为前三阶的加速度频谱幅值(A1、A2、A3)、该幅值下对应的频率(ω1、ω2、ω3)以及前三阶谐波荷载幅值(PGR 01、PGR 02、PGR 03)，待求参数为m，c，k。本文拟采用最小二乘法求解该非线性方程组。初值的定义比较困难，结合文献[12，14]，对于每个测试对象，质量的上限值应为该测试对象的质量，下限定义为0；对于刚度，当人直立站着不动的时候认为是行走时的刚度上限；而对于阻尼，由于人身体与踏步板接触时间的差异，人在站着的时候比行走情况下会吸收更多的振动能量，此时的阻尼值被认为是该模型阻尼的上限值。刚度、阻尼的下限值的定义参考文献[14]，各参数的取值范围以及初值如表2所示，表中M为测试者的质量。对于某些测试者来说，他们的数据可能会无法很好地吻合方程式(5)，在一些方程中出现误差较大，甚至无解的情况。这可能是因为采用的动力荷载因子本身也是统计值，对于某些个别测试者而言无法充分的应用。因此将一些误差较大的解去掉。

表2 参数的初值及范围

3.1 上楼梯的参数

3.1.1 参数的分布情况

通过上述方法获得的上楼梯时的人体动力学模型参数的统计值，如表3所示。

表3 求解得到的参数

为了验证求解出的人体动力学模型参数m，c，k的合理性，分别对此3个参数进行数学统计分析，明确各参数的分布情况，如图4所示。分析可知大致服从正态分布，而c，k均大致服从对数正态分布。

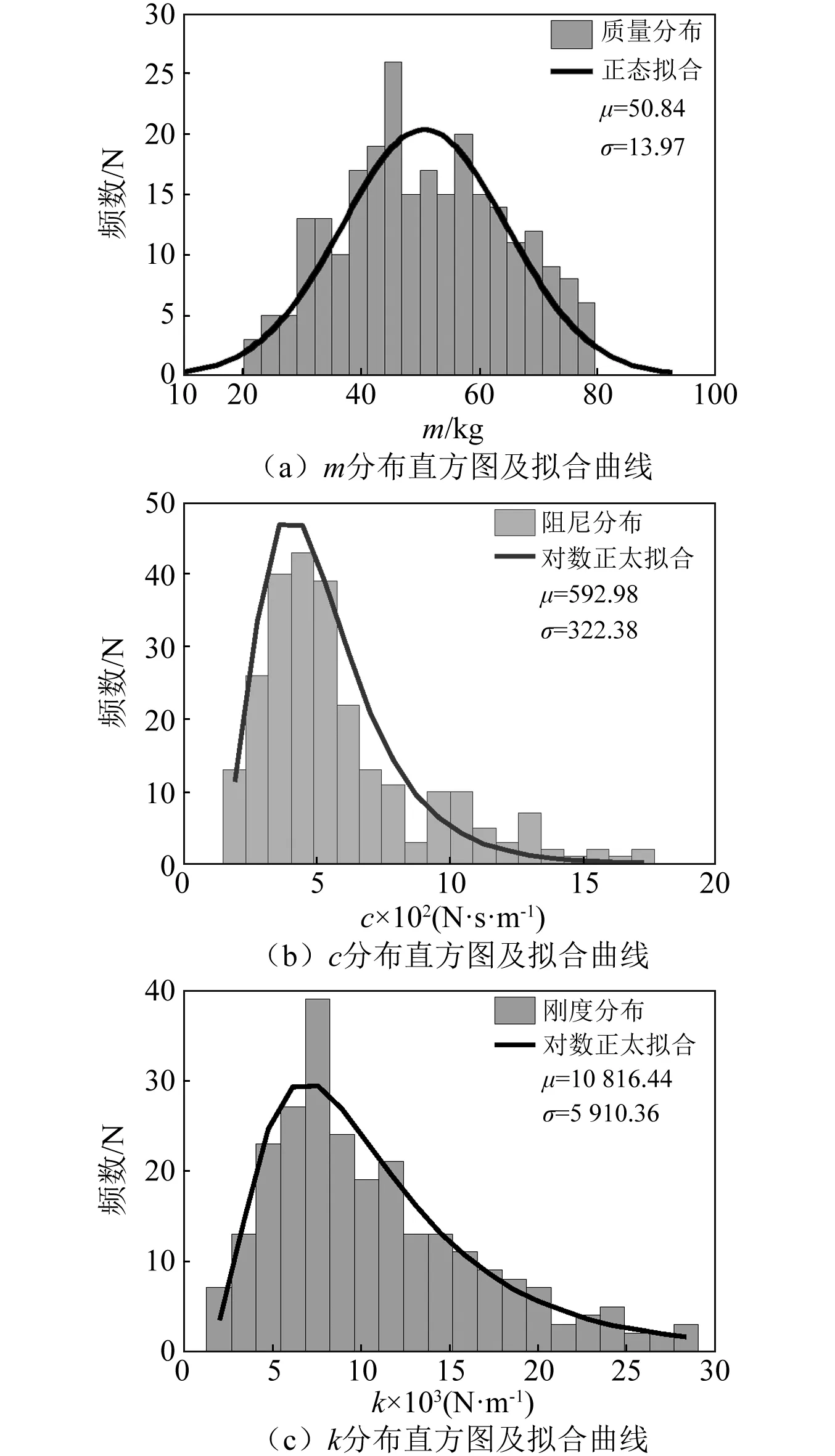
图4 各参数分布情况Fig.4 Distribution of each parameters

3.1.2 参数的相关性分析

对行人的人体动力学参数(m，c，k)以及人体质量M和步频fp进行相关性分析，由于组合类型较多，限于篇幅，此处只列出部分统计值R2和相关类型，R2值从0到1，R2值越大表明相关性越好，如表4所示。从表4可知，输入参数(M、fp)与输出参数(m，c，k)进行线性相关分析时，R2值相差较大。c，k均与fp相关性较大，这是因为人行走越快，fp越大，膝盖的弯曲程度越大，人与结构接触的时间越短，吸收的能量越少；而相比之下，m与M比m与fp相关性更大些，事实上，人体质量M与人体动力学模型的人体表观质量m理论上是具有较大相关性的。而总体来说，采用多变量进行含有交叉乘积项的二次回归分析时，拟合效果较好(95%的保证率)。

表4 相关性分析

3.1.3 参数的回归分析

建立人体动力学模型不仅是为了研究行人在行走时对结构产生的作用，更具有实际意义的是将该模型应用到工程中，更加准确的模拟和评估结构的振动特性，因此需要得到该模型中各参数的表达式。人体动力学模型参数主要包括m,c,k，采用M、fp进行回归分析。一般选用R2值较大的函数形式进行拟合，也就是采用含有交叉乘积项的二次回归拟合，拟合时尽量首先将输入值M、fp作为自变量，尤其是对于人体表观质量m，拟合时应当包含M；对于阻尼c，拟合时应当包含M；而刚度k在拟合时应当包含fp。因此结合表4，综合考虑之后，依次拟合c(M，fp)、k(c，fp)、m(M，k)。m,c,k拟合的表达式如表5所示，各数据点与拟合的曲面，如图5所示。

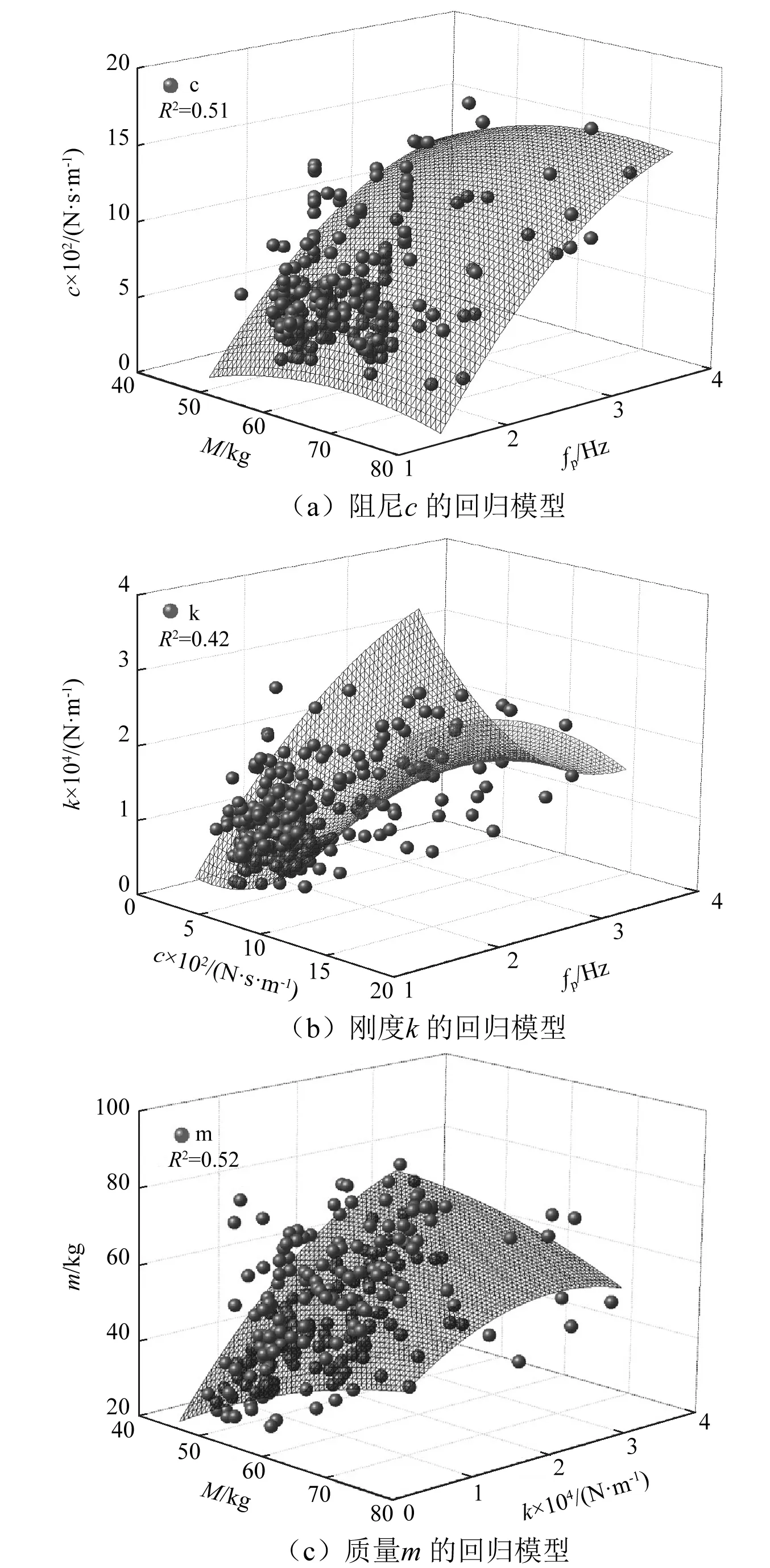
图5 各参数回归情况Fig.5 Regression of each parameters

回归表达式R2c(M,fp)=-0.424M2-203.861fp2+2.400Mfp+52.645M+1479.365fp-3343.7960.51k(c,fp)=0.0122c2-3697.673fp2-11.712cfp+8.774c+33882.611fp-36896.4680.42m(k,M)=-4.257×10-8k2-0.011M2-4.279×10-5kM+0.005k+2.214M-60.5810.52

3.2 下楼梯的参数

3.2.1 参数的分布情况

下楼梯时的人体动力学模型参数的研究过程类似于上楼梯的参数研究，而各参数的求解相对于上楼梯的求解较差，有效的解相对较少，m，c,k,M，fp的统计值如表6所示。

一般情况下，在保持行人能够顺畅的自由上下楼梯时，行人下楼梯时的步伐要快于上楼梯的步伐，从表6可以看出，步频fp的各项统计值均大于上楼梯的值，这与实际是相符的。结果发现下楼梯时人体动力学模型的人体表观质量m、阻尼c、刚度k的平均值均大于上楼梯时的参数值。分别对个参数进行数学统计分析，明确各参数的分布情况，如图4所示。同样的，分析可知m大致服从正态分布，而c,k均大致服从对数正态分布。

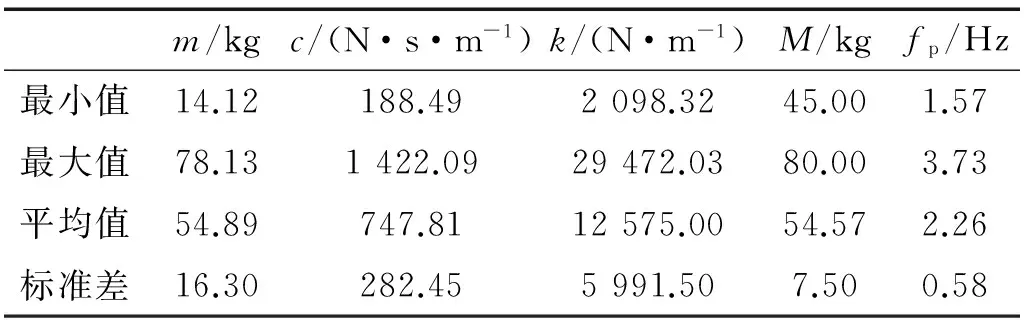
表6 求解得到的参数

3.2.2 参数的相关性分析

对行人的人体动力学参数(m,c,k)以及人体质量M和步频fp进行相关性分析，同样的，由于组合类型较多，此处只列出部分统计值R2和相关类型，如表7所示。从表7可知，输入参数(M、fp)与输出参数(m,c,k)进行线性相关分析时，c,k均与fp相关性较大，这一点与上楼梯时的一致；而与上楼梯时相反的是，m与fp比m与M相关性更大些。显然采用多变量进行含有交叉乘积项的二次回归分析时，动力学参数与其他变量的相关性明显提高。

表7 相关性分析

3.2.3 参数的回归分析

依然选用R2值较大的函数形式进行拟合，选择含有交叉乘积项的二次回归拟合，拟合时尽量首选输入值M、fp作为自变量，而且对于人体表观质量m，拟合时应当包含M。因此结合表7，综合考虑之后，依次拟合m(M，fp)、c(M，fp)、k(m，fp)。m,c,k拟合的表达式如表8所示，各数据点与拟合的曲面如图6所示。

图6 各参数回归情况Fig.6 Regression of each parameters

回归表达式R2m(M,fp)=-0.05M2-11.70fp2+0.02Mfp+6.17M+42.03fp-172.570.46c(M,fp)=-0.55M2-381.72fp2-7.19Mfp+93.67M+2646.67fp-5705.150.64k(m,fp)=-11.0m2-5204.25fp2-255.77mfp+1959.54m+48725.80fp-110532.820.57

对于确定的行人按照确定的步频行走时，如果已知该行人的质量，则可以得到该行人的人体动力学参数，即获得单个人的力学模型，进而可以结合人群的密度模拟人群效应。

4 结 论

本文参考楼板结构上的人体动力学模型的研究方法，分别对行人上、下楼梯的行走过程建立人体动力学模型，包含质量m、阻尼c、刚度k三个参数。首先将该模型等效为以m,c,k为未知数的三元非线性方程组，基于行人在楼梯上行走活动的竖向加速度数据，结合楼梯上的荷载模型，求解得到m,c,k三个参数。并且对m,c,k进行相关性分析，采用二次曲面拟合得到m,c,k的计算公式，为上、下柔性楼梯的人致振动响应计算提供了人体动力学模型。

[ 1 ] 陈隽, 彭怡欣, 王玲. 基于步态分析技术的三向单足落步荷载曲线试验建模[J]. 土木工程学报, 2014(3):79-87.

CHEN Jun, PENG Yixin, WANG Ling. Experimental investigation and mathematical modeling of single footfall load using motion capture technology[J]. China Civil Engineering Journal, 2014(3):79-87.

[ 2 ] 陈隽, 王浩祺, 彭怡欣. 行走激励的傅里叶级数模型及其参数的实验研究[J]. 振动与冲击, 2014, 33(8):11-15.

CHEN Jun,WANG Haoqi, PENG Yixin. Experimental investigation on Fourier-series model of walking load and its coefficients[J]. Journal of Vibration And Shock, 2014, 33(8):11-15.

[ 3 ] 丁国, 陈隽. 行人荷载随机性对楼盖振动响应的影响研究[J]. 振动工程学报, 2016, 29(1):123-131.

DING Guo, CHEN Jun. Influence of walking load randomness on vibration responses of long-span floor[J]. Journal of Vibration Engineering, 2016, 29(1):123-131.

[ 4 ] BISHOP N W M, WILLFORD M, PUMPHREY R. Human induced loading of flexible staircases[J]. Safety Science, 2001, 18(4):261-276.

[ 5 ] KERR S C, BISHOP N W M. Human induced loading on flexible staircases[J]. Engineering Structures, 2001, 23: 37-45.

[ 6 ] GAILE L, RADINSH I. Human induced dynamic loading on stairs [J]. World Academy of Science, Engineering and Technology, 2012(6): 1271-1277.

[ 7 ] BARKER C, MACKENZIE D. Calibration of the UK Nationnal Annex. Footbridge 2008[C]. Proceedings of the International Conference. Porto, Portugal, 2008.

[ 8 ] 秦敬伟, 杨庆山, 杨娜. 人体-结构系统静态耦合的模态参数[J]. 振动与冲击, 2012, 31(15):150-157.

QIN Jingwei, YANG Qingshan,YANG Na. Modal parameters of human body-structure static interaction systems[J].Journal of Vibration And Shock, 2012, 31(15):150-157.

[ 9 ] 秦敬伟, 杨庆山. 基于双足步行模型和反馈机制的人体-结构相互作用[J]. 建筑结构学报, 2014, 35(增刊1):18-24.

QIN Jingwei, YANG Qingshan. Human-structure interaction based on bipedal walking model and feedback mechanism[J]. Journal of Building Structures, 2014, 35(Sup1):18-24.

[10] KIM S H, CHO K I, CHOI M S, et al. Development of human body model for the dynamic analysis of footbridges under pedestrian induced excitation[J]. International Journal of Steel Structures, 2008, 8(4):333-345.

[11] 全国机械振动冲击与状态监测标准化技术委员会，中国质检出版社第三室.机械振动、冲击与状态监测国家标准汇编.人体振动与冲击卷[M].北京：中国质检出版社，2011.

[12] DA SILVA F T, Pimentel R L. Biodynamic walking model for vibration serviceability of footbridges in vertical direction[C]// Proceedings of the 8th International Conference on Structural Dynamics, EURODYN 2011, Leuven, Belgium. 2011: 1090-1096.

[13] TOSO M A, GOMES H M, SILVA F T D, et al. Experimentally fitted biodynamic models for pedestrian-structure interaction in walking situations[J]. Mechanical Systems & Signal Processing, 2015, 72/73:590-606.

[14] PAVIC A, REYNOLDS P, SACHSE R. Human-structure dynamic interaction in civil engineering dynamics: a literature review[J]. Shock & Vibration Digest, 2003, 35(1):3-18.

[15] 杜永锋，刘路路，朱前坤，等.上下楼梯时人行荷载模型参数的试验研究[J]. 振动与冲击, 2016，35(21)：220-228

DU Yongfeng，LIU Lulu,ZHU Qiankun,et al. Tests for parameters of pedestrian load model during human walking up and down stairs[J].Journal of Vibration and Shock,2016，35(21)：220-228