非一致性地震作用下跨越地裂缝结构的动力响应研究

熊仲明， 韦 俊，2， 郭亚雷， 王丙锐

(1.西安建筑科技大学 土木工程学院，西安 710055；2.苏州科技大学 机械工程学院，江苏 苏州 215009)

地裂缝是一种由内外力及人类活动等因素共同作用所形成的地面开裂现象，它普遍存在于许多国家，是一种世界性的地质灾害。我国地裂缝灾害比较严重，据统计全国出现了1 003处、6 000多条具有一定规模的地裂缝，其中以汾-渭盆地地裂缝带最为典型[1-4]。西安是地裂缝灾害非常严重的城市，自20世纪50年代在西安城南小寨和西北大学等地发现地裂缝以来，西安市已经发现了14条地裂缝带，总长度超过120 km[5]。

目前地裂缝研究还不成熟，基于建筑结构安全考虑，通常采用避让的做法，这样不仅严重制约着城市的规划和发展，而且导致土地资源的闲置和浪费。在西安城市发展建设过程中，城市的道路、地铁、输送管道等，有时不得不穿过地裂缝。随着西安市地裂缝活动性减弱并趋于稳定，进行跨越地裂缝非一致性地震作用下破坏机理的研究，对城市土地资源的合理利用具有十分积极的意义。

1 地裂缝环境下框架结构精细化模型建立与分析

1.1 地裂缝环境下框架结构精细化建模的方法

目前有限元数值模拟地裂缝场地时，常常把空间问题简化为平面问题，采用二维模型，仅在模型两端施加土体边界条件，没有考虑地裂缝带土体的差异性。

为了更加准确地研究跨地裂缝框架结构在地震作用下的动力响应规律，本文利用ABAQUS有限元分析软件，建立了三维实体模型，在模型周围施加土体边界条件，并考虑了地裂缝带土体的差异性。同时，在上部结构中考虑梁柱纵筋的位置、数量及箍筋的间距。为了保证计算精度，减少计算代价，通过模拟计算分析确定建模过程中单元类型、网格尺寸等各项参数。

ABAQUS中混凝土本构模型主要采用损伤塑性模型和弥散裂纹模型。损伤塑性模型使用各向同性损伤弹性结合各向同性拉伸和压缩塑性的模式来表示混凝土的非弹性行为，它引入了损伤因子来描述损伤，较弥散裂纹模型具有更好的收敛性和优越性[6]。因此本文选用混凝土损伤塑形模型，模型中选用的本构关系为规范中所推荐的应力-应变曲线，钢筋采用理想弹塑性模型。

1.2 跨地裂缝框架结构有限元单元类型和网格尺寸的确定

框架模型中钢筋采用三维桁架T3D2单元。为了保证计算精度和减少计算代价，合理确定混凝土三维实体主单元，本文选取了高度为5 m，截面尺寸为0.5 m×0.5 m的柱，利用有限元ABAQUS软件，采用不同网格尺寸的线性缩减积分单元(C3D8R)和非协调单元(C3D8I)分别进行了柱在横向水平力F=7 500 N作用下的侧移和周期计算对比，结果数据见表1所示。其计算参数为：混凝土密度ρ=2 400 kg/m3，泊松比υ=0.2，弹性模量E=3.0×1010N/m2。

其中柱计算的水平刚度和侧移为：

采用等效质量法求解模型的基本周期，如图1所示，计算得出周期T=0.09 s。

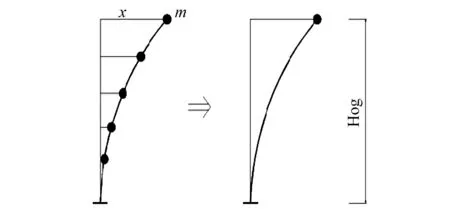
图1 单质点体系等效多质点体系示意图Fig.1 DOF is equivalent to multi particle system

从表1可以看出，在相同网格尺寸下，非协调单元的计算精度普遍高于缩减积分单元。同时可以看出，缩减积分单元在构件厚度方向至少要划分4个以上网格才能够得出可接受的结果。而非协调单元的精度较高，即使厚度方向只有一个单元，得出的结果也十分准确。但在计算过程发现非协调单元在网格划分中一定要保证不出现严重扭曲的网格。因此，在跨地裂缝框架结构建模时本文混凝土采用了C3D8I单元，在柱厚度方向至少划分了两个单元。

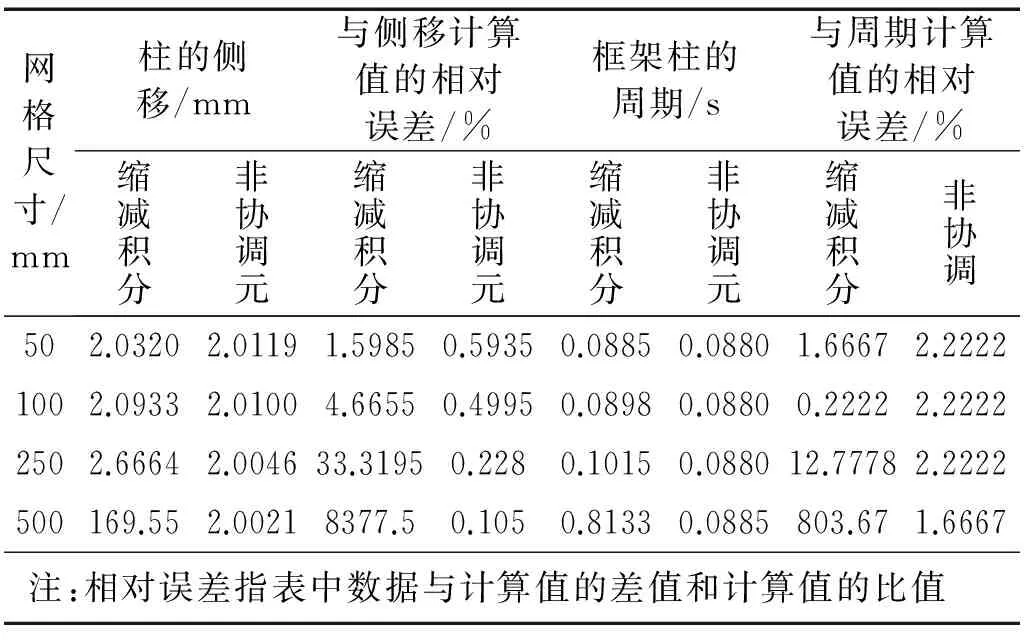
表1 柱在不同网格尺寸有限元模拟下横向力作用下的侧移和周期计算值

1.3 跨地裂缝框架结构模型

参考课题组所做的振动台模型试验和中煤西安设计工程公司的跨地裂缝框架结构，本文利用PKPM设计了一个平面尺寸为18 m×16.8 m的三层框架结构。框架结构的平面布置如图2所示，各层层高为3.6 m，板厚120 mm，柱尺寸为500 mm×500 mm，梁截面尺寸为300 mm×600 mm。混凝土强度等级采用C30，受力钢筋采用HRB400，箍筋采用HPB300。框架结构的楼板厚120 mm，柱尺寸为500 mm×500 mm，梁截面尺寸为300 mm×600 mm。框架结构的楼面恒荷载取5.0 kN/m2，屋面恒载取为7.5 kN/m2，楼面活荷载取3.5 kN/m2，屋面活荷载取为2.0 kN/m2。梁上线荷载楼面取值7.5 kN/m，屋面取值4.5 kN/m。提取出配筋信息，然后在ABAQUS中建立包含钢筋的三维实体有限元模型，楼板采用C4R壳单元，框架模型如图3所示。

图2 框架结构平面布置图(mm)Fig.2 Plan layout of frame structure(mm)

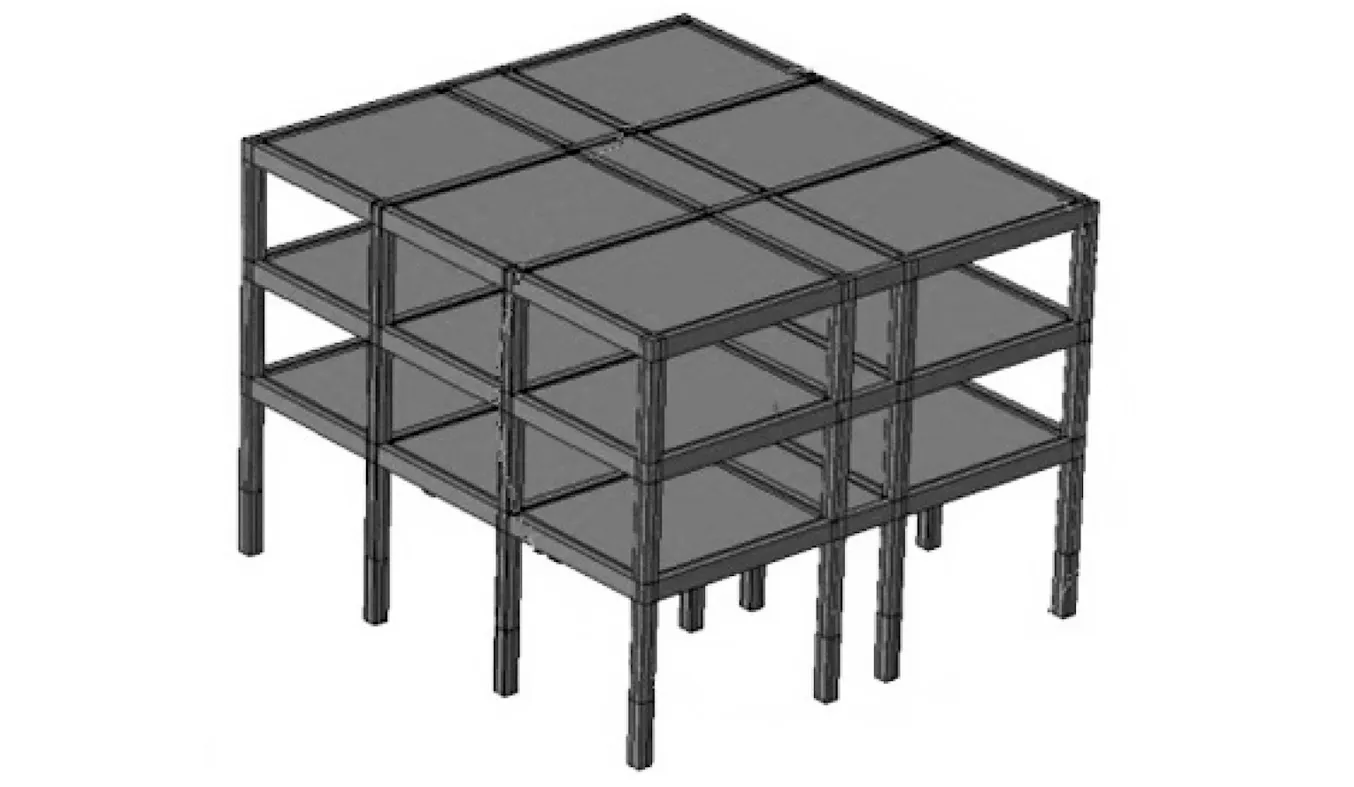
图3 框架结构模型Fig.3 Model of frame structure

2 场地土体建模分析

2.1 有限元模型的建立

地裂缝的存在破坏了场地的完整性，地裂缝场地与普通场地在地震作用下会呈现出不同的特性。参考《唐延路地下人防工程岩土工程地勘报告》[7]中地裂缝场地土体的各项指标参数，在考虑上部结构边界效应的基础上，参考有关文献及计算工作量，选取土体模型几何尺寸为90 m×60 m×20 m(长×宽×深)。将模型中场地土体被分为素填土、黄土状土、黄土、古土壤、粉质黏土五层。土体材料采用摩尔库仑弹塑性模型，由于场地中存在裂缝，因而不可避免的存在扭曲网格，故土体单元采用C3D8,各土层指标参数见表2。根据地裂缝场地的振动台试验结果，模拟中地裂缝的倾角从下至上一致取为80°。为了更有效直观地表明地裂缝场地的地震作用效应，本文分别建立了普通场地与地裂缝场地两种数值计算模型，其剖面如图4和图5所示。

图4 普通场地各土层分布图(mm)Fig. 4 Distribution of soil layers in common ground (mm)

图5 地裂缝场地各土层分布图(mm)Fig. 5 Distribution of soil layers in ground fissure(mm)

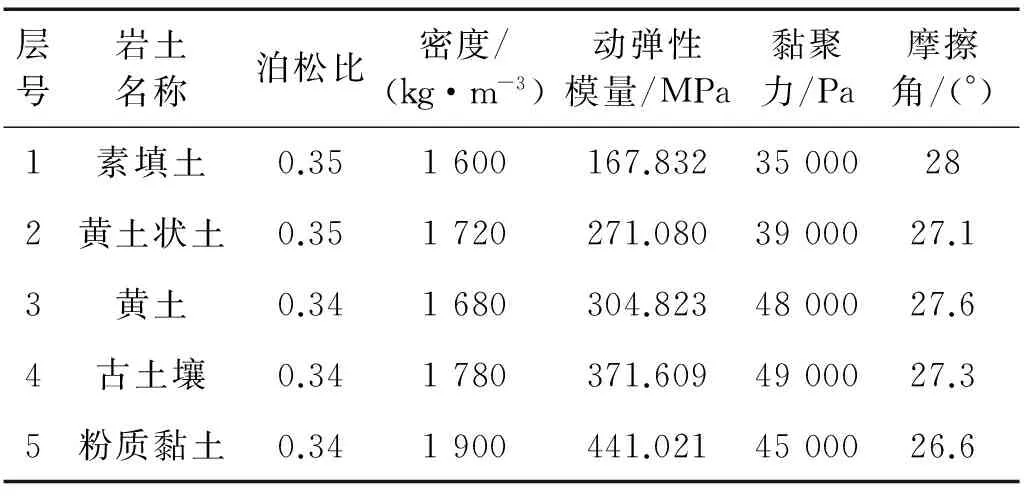
层号岩土名称泊松比密度/(kg·m-3)动弹性模量/MPa黏聚力/Pa摩擦角/(°)1素填土0.351600167.83235000282黄土状土0.351720271.0803900027.13黄土0.341680304.8234800027.64古土壤0.341780371.6094900027.35粉质黏土0.341900441.0214500026.6

2.2 地裂缝带的模拟

地裂缝带和非地裂缝带土体的力学性质存在显著差异。参考文献[8-9]所得成果，对地裂缝带上盘土体宽度取为4.5 m,下盘土体宽度取为2 m，从地表往下逐渐尖灭。对地裂缝带中的土体弹性模量、黏聚力和摩擦角均考虑15%劣化，而密度考虑5%提高，以此来模拟地裂缝带土体的差异性。对裂缝处上下盘土体的相互作用，采用ABAQUS面接触中的有限滑移，法向为硬接触，即两物体只在压紧状态时才传递法向压力，而切向作用采用罚摩擦公式，摩擦因数取0.3。

2.3 边界条件的设置

土体是无限空间体，采用有限元方法分析时需要从中截取一块区域，要使数值模拟接近实际情况就需要在截取区域的边界上建立一定的人工边界来模拟连续介质的辐射阻尼，使得波动从边界穿过时不会产生反射效应[10-11]。人工边界条件参考文献[12-13]的研究成果，采用等效三维一致黏弹性单元，其方法为在边界上延伸一层厚度相近的三维八节点六面体实体单元，将外层边界固定。三维八节点六面体实体单元的各项参数按照以下公式取值:

α=αN/αT

(1)

(2)

(3)

(4)

式中：E为边界单元的等效弹性模量；η为刚度阻尼系数。

2.4 地裂缝场地土体模型计算结果与试验结果的对比

为了充分研究地裂缝场地地震作用效应，本课题组在西安建筑科技大学工程抗震与结构实验室进行了地裂缝场地振动台模型试验。试验中土箱尺寸为3.0 m×1.5 m×1.5 m(长×宽×高)；箱体采用层状剪切模型箱，共14层，层间距为12 mm，每层框架为100 mm×100 mm×2 mm(长×宽×厚)的空心方形钢管；除了底层框架外，其余各层之间沿振动方向放置凹槽，每边各3个，凹槽里放滚珠和涂抹润滑油，从而形成自由滑动的支点，土箱如图6所示。试验土体是在西安f4地裂缝土层分布的基础上进行了简化和小幅修改，土体分为黄土、古土壤、粉质粘土三层，基本物理力学指标见表3，试验模型见图7，试验土层分布见图8。

表3 地裂缝场地土体基本物理力学指标

图6 土箱实物图Fig.6 Physical map of soil box

图7 地裂缝场地试验模型Fig. 7 Experimental model of ground fissure

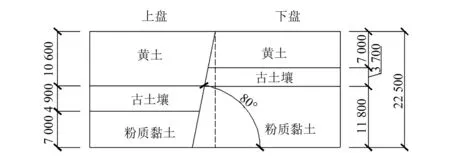
图8 试验土层分布Fig. 8 Distribution of test soil layer

图9是在峰值加速度为0.4 g的EL-Centro波作用下，数值模拟的地表加速度和试验测试加速度值。其中虚线处为地裂缝位置。图9表明，对于地裂缝场地的地震放大效应，数值模拟结果和试验结果得出了相同的规律，地表峰值加速度在地裂缝处最大，从地裂缝处向两侧递减，地裂缝场地土体对输入地震加速度具有放大作用。这不但表明了地裂缝场地土体加速度放大效应规律，也表明数值模拟的合理性和可靠性。

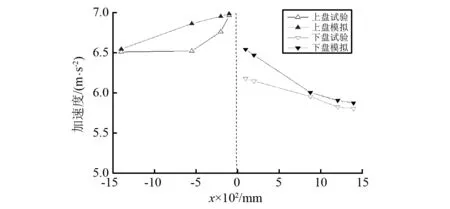
图9 试验与模拟地表峰值加速度对比图Fig.9 Collation map of peak ground acceleration in experiment and simulation

3 跨地裂缝框架结构时程分析

在数值模型中框架结构和场地土体之间的连接采用的方法是将柱子埋入土体中2 m，框架柱与周围土体通过接触中的tie方式进行连接，这样土体和框架柱底部的位移和变形是耦合的，可以充分考虑土体与框架柱的相互作用，比较接近实际情况。模型如图10和图11所示。

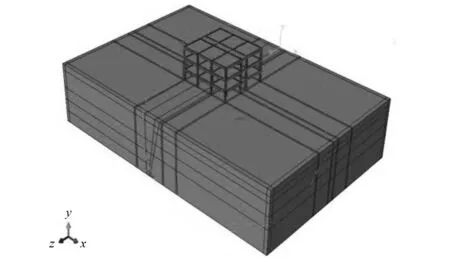
图10 跨地裂缝框架有限元模型Fig.10 Finite element model of frame cross ground fissure

图11 普通场地框架有限元模型Fig.11 Finite element model of frame cross common ground

表4、表5和表6分别为采用EL-Centro波、Northridge波和一条上海人工波，在加速度峰值分别为70 gal、200 gal和400 gal三种工况下，普通场地和地裂缝场地框架结构的层间位移、层间位移角和增大幅度的对比。其中有效的持续时间为结构周期的5倍～10倍，地震波都选取了10 s。

表4 EL-Centro波作用下框架结构层间位移及层间位移角

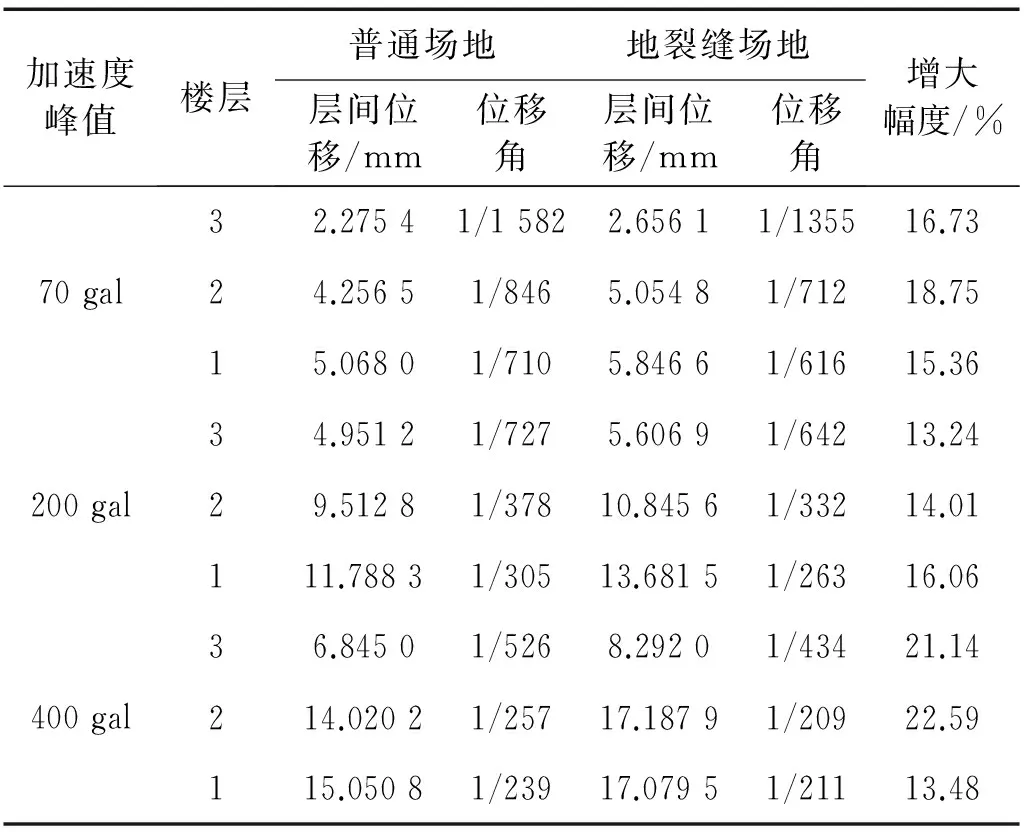
表5 Northridge波作用下框架结构层间位移及层间位移角

由表4、表5和表6可以看出，在70 gal、200 gal和400 gal地震作用下，两种场地框架结构的层间位移均表现出一层最大，从下往上依次递减的规律。由表4可以看出，当地震强度70 gal时，EL-Centro波框架结构3层的层间位移在地裂缝场地和普通场地分别为2.215 mm和1.943 5 mm；当地震强度400 gal时，地裂缝场地和普通场地分别为15.120 mm和14.291 mm,其地裂缝场地位移均明显大于普通场地。表5和表6也有类似的结果。因此可以得出，在三种地震类型和不同强度作用下，跨地裂缝框架结构的层间位移均大于普通场地。地裂缝的存在使上部框架结构的层间位移变大，且加剧了上部框架结构的破坏，对上部结构具有不利作用。由表4、表5和表6还可以看出，在70 gal地震作用下，框架结构的层间位移角均小于抗震规范中规定的弹性层间位移角限值1/550，表明框架结构均处于弹性状态，跨地裂缝框架层间位移角在上海人工波作用时最大，其值为1/614；在200 gal和400 gal地震作用下，框架结构的最大层间位移角均大于1/550，但小于抗震规范中弹塑性层间位移角限值1/50，可认为框架结构处于弹塑性变形阶段，且框架结构有良好的延性，跨地裂缝框架在400 gal时的层间位移角最大，其值为1/98。由表4、表5和表6还可看出增大幅度没有明显的规律，但其值大小均在30%以内。

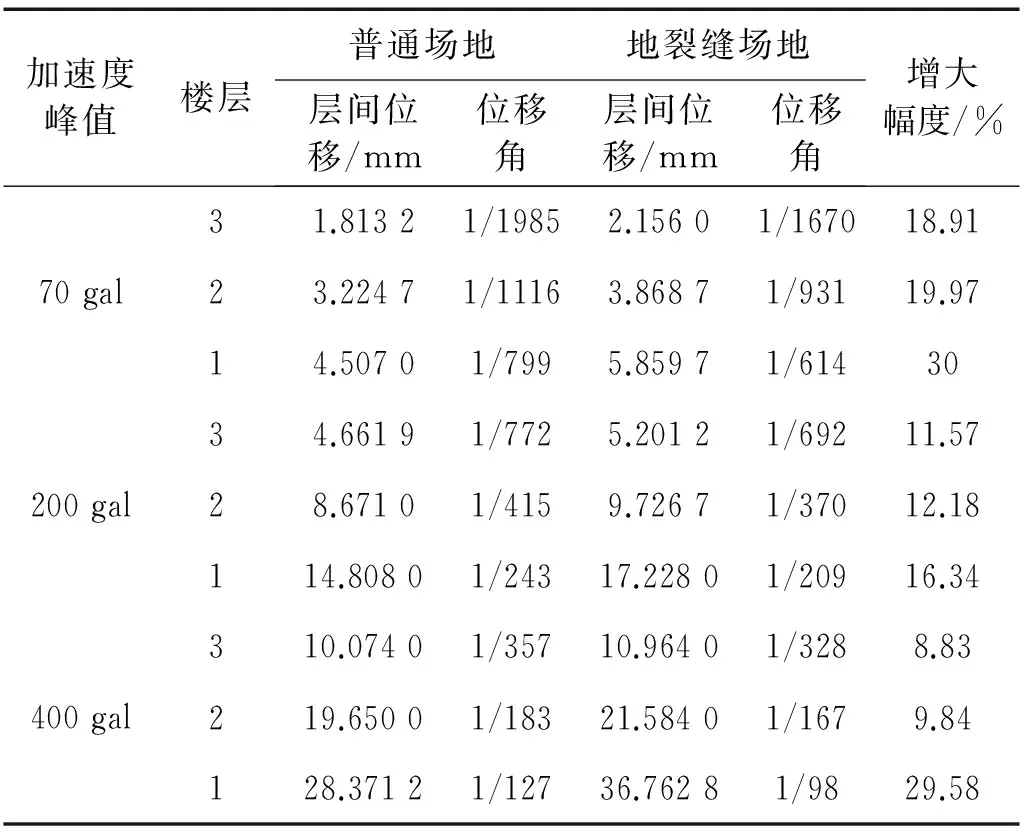
表6 上海人工波作用下框架结构层间位移及层间位移角

4 结 论

对跨地裂缝框架结构和普通场地框架结构进行了时程分析，对比了地裂缝场地非一致性地震激励下框架结构的地震响应和普通场地框架结构的地震响应，得出以下结论：

(1)计算结果表明，地震作用时，地裂缝场地地表峰值加速度呈现出在裂缝处最大，并从地裂缝处向两侧逐渐减小的规律。

(2)在不同地震类型和强度作用下，跨地裂缝框架结构的层间位移均大于普通场地框架结构，计算结果表明地震作用时地裂缝的存在加剧了上部结构的破坏，对上部结构具有不利作用，地裂缝场地对上部结构的危害性严重于普通场地。

(3)计算结果表明，地震时地裂缝的存在在一定范围内对上部结构有影响。但在活动性较弱或趋于稳定的地裂缝上设计简单结构是可行的，对跨地裂缝结构采取一定程度的加固或减震耗能等技术措施后可以避免跨地裂缝结构的地震灾害。

(4)计算结果表明，跨地裂缝结构的地震响应与地震类型、地震强度、楼层位置有关。随着地震强度的增大，跨地裂缝结构动力响应显著增大。

[ 1 ] 黄强兵,彭建兵,闫金凯，等.地裂缝活动对土体应力与变形影响的试验研究[J].岩土力学,2009,30(4): 903-908.

HUANG Qiangbing, PENG Jianbing, YAN Jinkai, et al. Model test study of influence of ground fissure movement on stress and deformation of soil mass[J]. Rock and Soil Mechanics, 2009,30(4): 903-908.

[ 2 ] 焦珣,苏小四,于军，等.苏锡常地裂缝危险性分区[J].吉林大学学报(地球科学版),2009,39(1): 142-146.

JIAO Xun, SU Xiaosi, YU Jun，et al. Fatalness zoning of earth fissure harzard in Suzhou-wuxi-changzhou area[J]. Journal of Jilin University (Earth Science Edition),2009, 39(1): 142-146.

[ 3 ] 王景明.地裂缝及其灾害的理论与应用[M].西安:陕西科学技术出社,2000.

[ 4 ] 孙绍平,韩阳.生命线地震工程研究述评[J].土木工程学报,2003,36(5): 97-104.

SUN Shaoping, HAN Yang. State-of-the-art of the research on lifeline earthquake engineering[J]. China Civil Engineering journal, 2003,36(5): 97-104.

[ 5 ] 张鹏.地裂缝在近地表土层中的破裂行为研究[D].西安:长安大学,2012.

[ 6 ] 何玉阳，袁泉. 基于振动台试验的框支密肋复合墙结构弹塑性有限元分析[J]. 振动与冲击, 2015, 34(13): 205-210.

HE Yuyang, YUAN Quan. Frame supported multi ribbed composite wall structure elastic-plastic finite element analysis based on vibration test[J]. Journal of Vibration and Shock, 2015, 34(13): 205-210.

[ 7 ] 西北综合勘测设计研究院.唐延路地下人防工程岩土工程地勘报[R].2013.

[ 8 ] 胡志平,赵振荣,朱启东，等.西安某地裂缝两侧黄土物理力学性质试验[J].地球科学与环境学报,2009,31(1): 85-88.

HU Zhiping, ZHAO Zhenrong, ZHU Qidong, et al. Experimental study on physical mechanic property of loess near ground fissure in Xi’an[J]. Journal of Earth Sciences and Environment, 2009,31(1): 85-88.

[ 9 ] 李忠生,刘芳,高铎文,等.西安地裂缝变形带中的剪切波速测试分析[J].水文地质工程地质,2008,35(6): 95-98.

LI Zhongsheng, LIU Fang, GAO Duowen, et al. Tests and analyses of shearing wave velocity in the Xi'an earth fissure deforming belt[J]. Hydrogeology & Engineering Geology, 2008,35(6): 95-98.

[10] 廖振鹏,刘晶波.波动有限元模拟的基本问题[J].中国科学(B辑化学生命科学地学),1992(8): 874-882.

LIAO Zhenpeng, LIU Jingbo. Basic problems in finite element simulation of wave[J]. Science china(Chemistry life sciences B), 1992 (8): 874-882.

[11] 刘晶波,吕彦东.结构-地基动力相互作用问题分析的一种直接方法[J].土木工程学报,1998,31(3): 55-64.

LIU Jingbo, LÜ Yandong. A direct method for analysis of dynamic soil-structure interaction[J]. China Civil Engineering Journal, 1998,31(3): 55-64.

[12] 谷音,刘晶波,杜义欣,等.三维一致黏弹性人工边界及等效黏弹性边界单元[J].工程力学,2007,24(12): 31-37.

GU Yin, LIU Jingbo, DU Yixin, et al. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007,24(12): 31-37.

[13] 高峰，赵冯兵.地下结构静一动力分析中的人工边界转换方法研究[J]. 振动与冲击, 2011, 30(11): 165-170.

GAO Feng，ZHAO Fengbing .Study on transformation method for artificial boundaries in static-dynamic analysis of underground structure[J]. Journal of Vibration and Shock, 2011,30(11): 165-170.