热环境下长宽比对L型折板统计能量分析参数的影响研究

陈 强， 张 鹏， 李彦斌， 吴邵庆,2， 费庆国,2

(1.东南大学 土木工程学院，南京 210096；2. 东南大学 江苏省工程力学分析重点实验室，南京 210096)

高速飞行器在飞行过程中面临着复杂严酷的高温、振动和噪声环境[1-2]。高温使材料性能参数发生变化同时也改变结构的应力分布状态[3-4]，进而导致结构的动力学特性呈现出与常温环境不同的规律，因此热效应是结构动力学分析中必须考虑的因素。同时，飞行器所面临的动力学环境频谱较宽，其中振动的频率范围为0～2 000 Hz，噪声的频率范围可达10～10 000 Hz，目前针对高频段的动力学分析常采用统计能量分析[5](Statistical Energy Analysis, SEA)方法进行研究。

统计能量分析方法将研究对象从随机参数描述的总体中抽取出来，忽略被研究对象的具体细节，进而使用统计的方法获取时域、频域和空间上的能量平均值，为解决复杂系统高频动力学问题提供了有力工具。目前统计能量分析方法已成功应用于航空航天、汽车及建筑等领域[6-8]。统计能量分析的精度主要取决于其分析参数的准确性，即系统的模态密度(Modal Density)、单个子系统的内损耗因子(Internal Loss Factor, ILF)、各个子系统间的耦合损耗因子(Coupling Loss Factor, CLF)。

结构几何尺寸对结构动力学特性、热应力和稳定性等有较大影响[9]，是结构设计优化中重点关注的因素。对于统计能量分析而言，结构几何尺寸对结构动力学特性的影响，主要通过统计能量分析参数的变化进行评估。目前国内外针对结构几何尺寸对结构的统计能量分析参数的影响已开展了相关研究。Pankaj等[10]分别采用理论方法、有限元法并结合Free-SEA软件研究了常温环境下耦合边尺寸对L型折板的耦合损耗因子的影响，发现耦合边长度对常温环境下结构的内损耗因子和耦合损耗因子影响不大。江民圣等[11]通过波方法研究了板厚对L型折板能量传递系数的影响。目前针对长宽比对统计能量分析参数影响的研究主要集中在常温环境下，涉及热环境下的研究较少。热效应所引起的材料力学性能参数变化及产生的热应力会使得结构的刚度发生变化，对结构动力学特性的影响不能忽视，因此有必要开展热环境下长宽比对L型折板统计能量分析参数的影响研究。

本文基于有限元法和计及热效应的功率输入法，针对高温和常温环境下长宽比对L型折板统计能量分析参数的影响开展研究。首先介绍基于波方法的统计能量分析参数解析解，阐述基于功率输入法和计及热效应功率流模型的数值方法；其次，对比数值解和解析解验证分析方法的准确性；最后，分析高温环境下长宽比对结构热应力的影响，开展高温和常温环境下长宽比对结构模态、内损耗因子和耦合损耗因子的影响研究。

1 理论基础

1.1 基于波方法的统计能量分析参数理论解

对于简单结构，如图1所示的L型板和T型板，通过波方法[9]可获取其在常温环境下的统计能量分析参数的理论解。

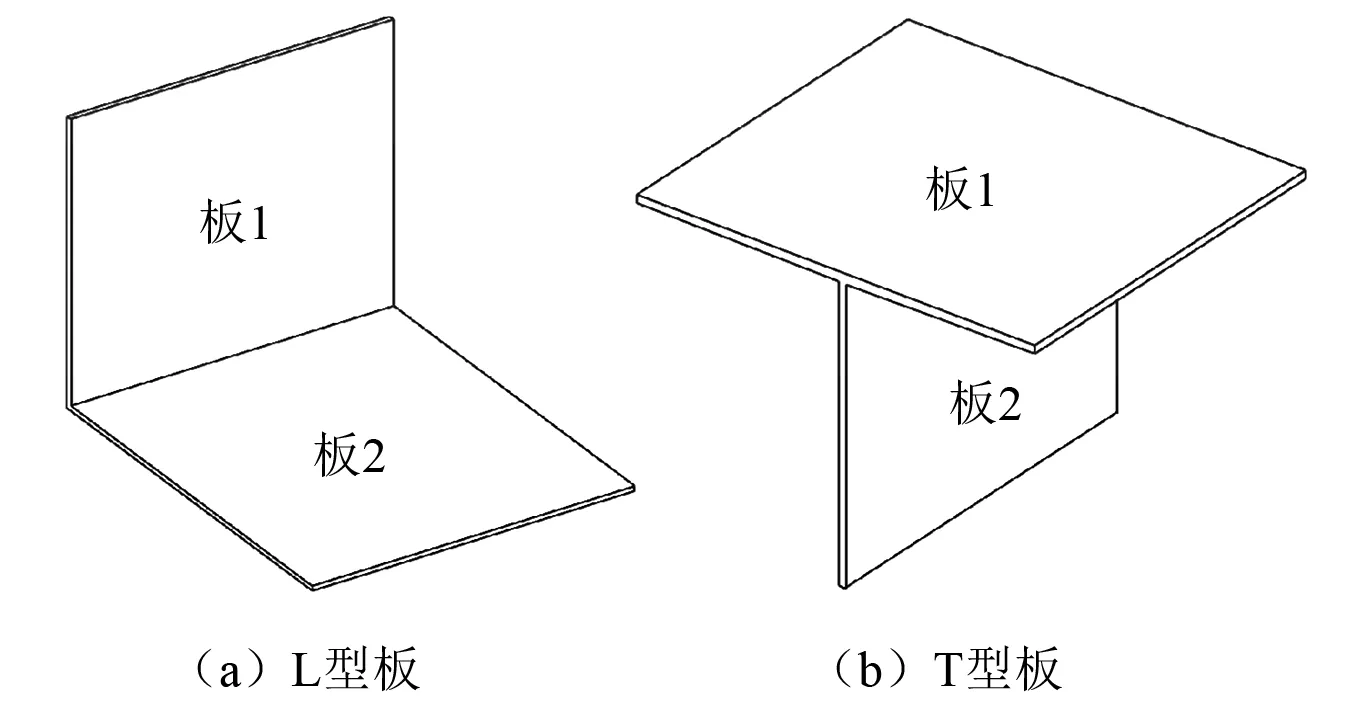
图1 简单结构示意图Fig. 1 Schematic diagram of simple structure

对于如图1(a)所示的L型折板，两板的内损耗因子相等，板1的内损耗因子η1：

η1=2ξ1

(1)

式中：ξ1为板1的平均模态阻尼比。

板1对板2的耦合损耗因子η12为[12]：

(2)

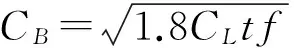
(3)

式中：X=t1/t2为两板厚度比；τ12(0)=2(φ1/2+φ-1/2)-2为常传递系数，其中φ的表达式为：

(4)

由式(1)～式(4)可知，长宽比是影响L型板结构统计能量分析参数的重要因素。

1.2 基于FEM-PIM方法统计能量分析参数的数值解

由于波方法仅适用于简单结构，难以推广至复杂结构。因此，本文采取有限元法(Finite Element Method，FEM)和功率输入法(Power Injection Method，PIM)获取结构的统计能量分析参数。具体步骤为：首先通过FEM获取系统的模态、质量矩阵和刚度矩阵；然后使用计及热效应的功率流模型计算结构的输入功率及振动能量；最后结合PIM获取结构的统计能量分析参数。

1.2.1 功率输入法

对于具有N个子系统的结构，其统计能量分析的动力学方程为：

ωη[E1,E2,…EN]T=[P1,P2,…PN]T

(5)

式中：ω为频带中心频率，Ei为子系统i在空间内和频域内的平均能量；Pi为子系统i在空间内和频域内的平均输入功率；η为耦合系统的总损耗因子矩阵。

对于耦合系统的总损耗因子矩阵η，其矩阵元素为：

(6)

式中：ηi为子系统i的内损耗因子；ηji为子系统j与子系统i间的耦合损耗因子。

仅在子系统i上施加输入功率为Pi的载荷时，有：

(7)

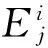
对于具有N个子系统的结构，逐一在各子系统上施加载荷，将得到的如式(7)类型的N个方程以矩阵形式表达为：

ωηE=P

(8)

已知P和E，即可得到耦合系统的总损耗因子矩阵η：

(9)

1.2.2 计及热效应的功率流模型

温度对结构刚度的影响主要体现在两方面：一方面，温度的升高使得材料的力学性能发生变化，导致其刚度改变；另一方面，结构在热应力的作用下产生附加应力刚度矩阵。因此，计及热效应的有限元动力学方程可表示为：

([Ks+KT+Kσ]+jωC-ω2M)ui=F

(10)

式中：Ks为常温下结构的刚度矩阵；KT为材料参数变化引起的刚度改变矩阵[13]；Kσ为热应力引起的附加刚度矩阵[14]；C和M分别为结构的阻尼矩阵和质量矩阵；u为节点位移；F为外载荷激励向量。

由计及热效应的有限元动力学方程可知，系统振动的势能T和动能V分别为：

(11)

式中：K=Ks+KT+Kσ为总体刚度矩阵。

对于L型折板结构，将其划分为a和b两个子系统。其中子系统b的响应向量ub可通过转化矩阵Zb获得，即ub=Zbu。系统b的势能Tb和动能Vb分别为：

(12)

式中：Kb和Mb分别为子系统b刚度矩阵和质量矩阵。

通过模态分析可获得系统前n阶模态质量归一化模态振型向量。记第j阶模态的振型向量为φj，前n阶模态振型向量组成的模态振型矩阵为Φ=[φ1,φ2,…,φn]。根据模态的正交性：

(13)

式中，ωj为第j模态的固有频率，j∈[1,n]。

第j阶模态受到的模态力Fj及其在该模态力作用下的位移响应Yj为：

(14)

当只在子系统a上施加载荷Fu时，在模态坐标系下，系统的振动动能V、势能T和对子系统a的输入功率Pin分别为：

(15)

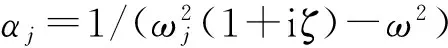
将式(14)代入式(12)中可得，模态坐标系下子系统b计及热效应的动能Vb和势能Tb分别为：

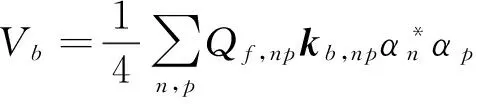
(16)

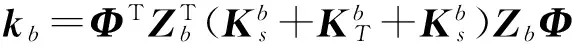
将计算得到的输入功率、子系统振动能量代入式(9)中即可得到结构的内损耗因子和耦合损耗因子。

2 数值仿真

为研究结构长宽比对统计能量分析参数的影响，本文以夹角为90°的L型对称折板为研究对象，其几何模型如图2所示，其中板厚t为1 mm、板宽L2为300 mm。板材料为TA7钛合金，材料属性如表1所示。采用壳单元建立其有限元模型，单元尺寸为5 mm。两板除耦合边外各边简支。在分析过程中结构阻尼参考文献[15]中的经验公式设置。

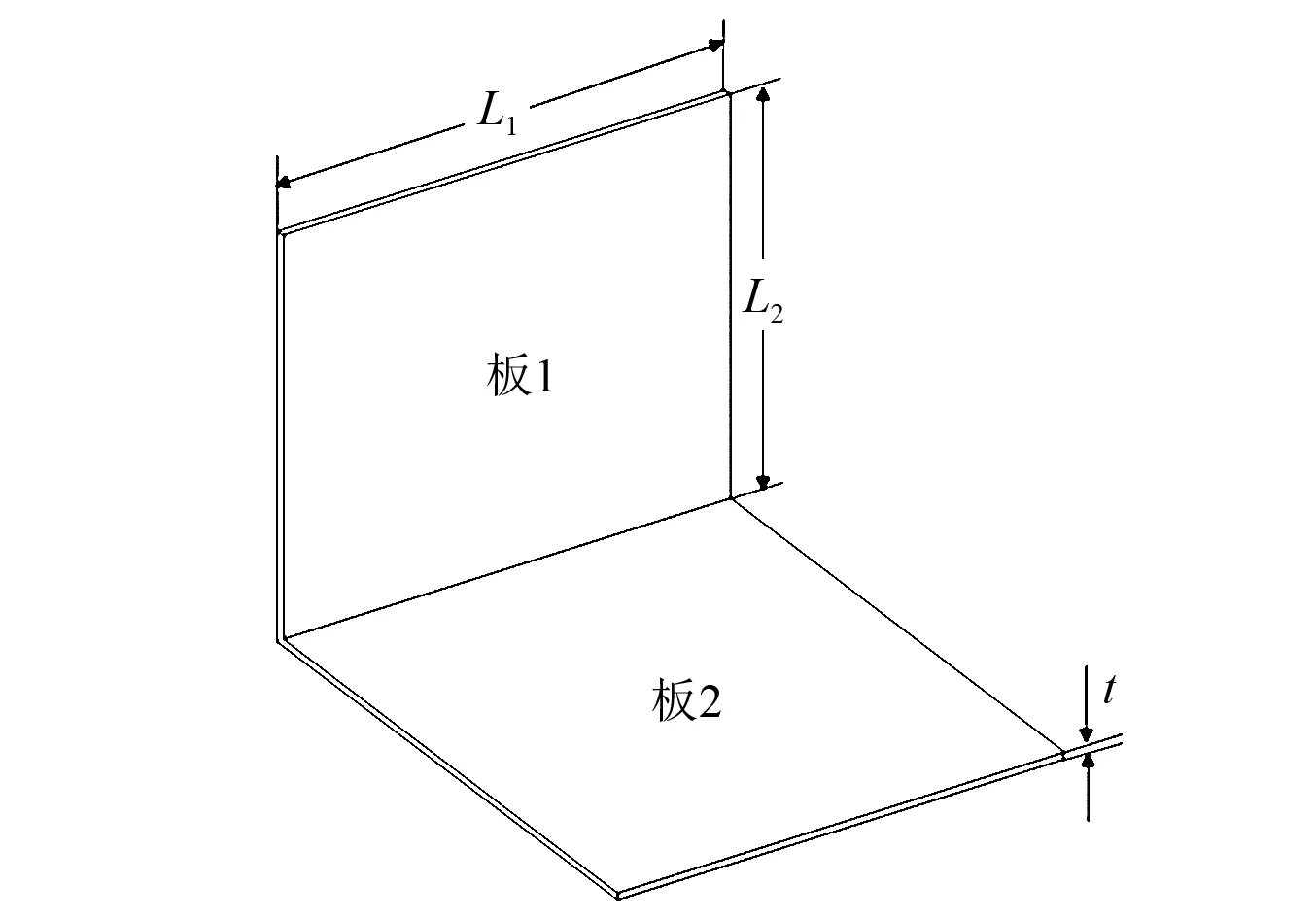
图2 L型对称折板Fig. 2 L-shaped symmetry folded plate

温度/℃弹性模量/GPa热膨胀系数×10-6/℃-1泊松比密度/(kg·m-3)20109.5-20098.18.90.334420

由于统计能量理论假设分析频带内各模态的振动能量相等，因此计算中宜选取对系统各阶模态输入功率相近的载荷。雨流载荷(Rain On the Roof，ROF)[16]是一种空间内各点互不相关的宽带激励，它可以均等地、充分地激励起子系统的局部模态，满足统计能量分析中频带内各模态振动能量相等的假设，因此在后续的算例中均在结构上施加单位雨流载荷。雨流载荷的载荷幅值与作用点的材料密度成正比，对于离散的有限元模型，雨流载荷对应式(15)中Qf里的矩阵A，满足A=S2M，其中S表示载荷强度。

由于统计能量分析理论中，同一个板内的不同模态群也被视为不同的子系统，即同一个板内的弯曲模态、面内模态、剪切模态被视为不同的子系统。对于夹角为90°的L型折板薄壁结构的振动由弯曲模态主导，可视为满足对称性。

2.1 方法验证

L型折板中的板1和板2分别对应子系统a和子系统b。首先进行常温(20℃)环境下长宽比L1/L2为1时的数值分析。在板1上施加垂直于面板方向的单位雨流载荷，基于FEM-PIM开展结构的统计能量分析。由式(9)计算得到板1的内损耗因子及板1对板2耦合损耗因子的数值解，并将二者与理论解进行对比分析，其中解析解可通过式(1)和式(2)计算得到，分别如图3和图4所示。计算结果表明，当频带中心频率低于1 000 Hz时，内损耗因子和耦合损耗因子与理论解相差较大，这是因为分析频段内模态数较少，未能满足统计能量分析中分析频带内模态数大于5的假设条件[5]。随着中心频率的增加，内损耗因子和耦合损耗因子均与理论解基本一致，在1 000 Hz至5 000 Hz频段内，内部损耗因子和耦合损耗因子的平均误差分别为0.6%和1.7%。

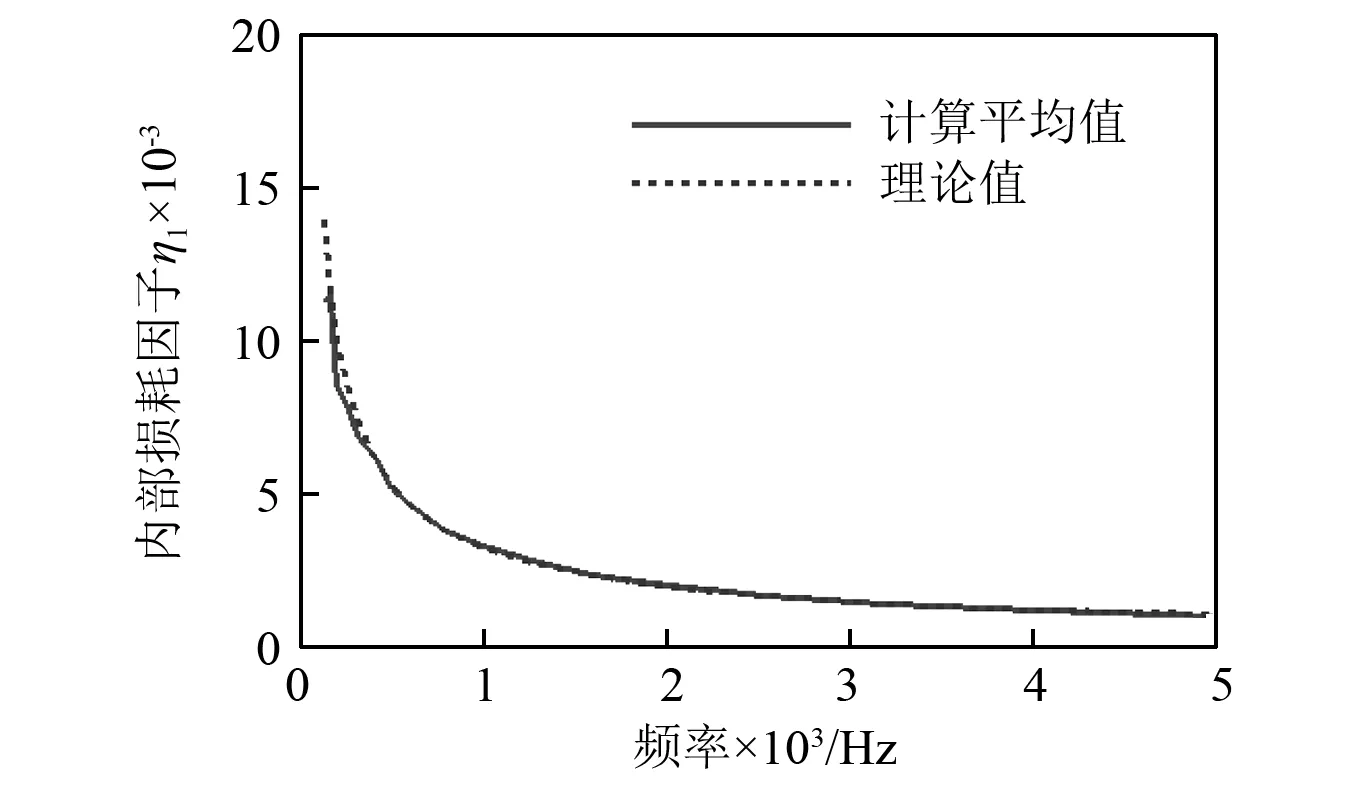
图3 板1的内损耗因子Fig. 3 ILF of plate 1

由于目前缺乏高温环境下统计能量分析参数的理论解，且高温环境下的高频试验开展难度较大。由式(15)和式(16)可知，本文采用的基于FEM-PIM计及热效应统计能量分析方法的准确性主要取决于热环境下系统的固有频率、模态振型、刚度矩阵和质量矩阵等参数的准确性。本文中这些参数主要通过有限元方法获得，目前计及热效应的结构有限元计算精度较高且已有较多研究成果[3-4]，因此本文采用的FEM-PIM方法在高温环境下统计能量分析所得结果也是可信的。

图4 板1对板2的耦合损耗因子Fig. 4 CLF of plate 1 to plate2

为研究结构长宽比对统计能量分析参数的影响，本文选取了长宽比L1/L2为0.5～1.4间共11个模型进行数值计算，开展常温和高温环境下结构的统计能量分析，其中高温环境中对结构施加200℃的均匀温度载荷。选取2 800 Hz～3 550 Hz频段Δω(中心频率为3 150 Hz)为分析频段。

2.2 长宽比对结构热应力的影响

表2给出了部分尺寸结构在热环境下热应力分布。由表2可知，长宽比对结构的热应力分布有较大影响，总体而言，结构热应力较大的位置均出现在耦合边及约束边界。同时，长宽比对结构热应力的幅值有较大影响，结构热应力的最大值整体呈现随长宽比增加逐渐减小的趋势。

2.3 长宽比对结构固有特性的影响

常温和高温环境下，11组模型中部分尺寸结构的第一阶模态如表3所示。计算结果表明：长宽比对结构的固有频率影响较大，随长宽比的增加，结构第一阶固有频率均逐渐降低。高温环境下结构第一阶固有频率高于常温环境下，这是由于高温使得结构发生了热变形，热变形在约束条件下使结构内部产生预拉或预压应力或二者同时存在，使得结构发生软化或硬化。常温环境下结构振型分布规律基本一致；高温环境下，长宽比对结构振型影响较大，产生了较多局部模态这主要是由于热应力较大的幅值和非均匀的分布造成的。热应力对结构的质量分布影响较小，但其产生的附加刚度改变了结构的整体刚度分布，从而使得结构振型发生变化。

常温和高温环境下Δω频带内模态密度如图5所示。计算结果表明：两种环境下长宽比的增加整体上使得模态更加密集；常温环境下的模态密度低于高温环境下的模态密度，这主要是因为在Δω频带内，高温引起的TA7钛合金材料弹性模量降低对结构固有特性影响占主导地位。

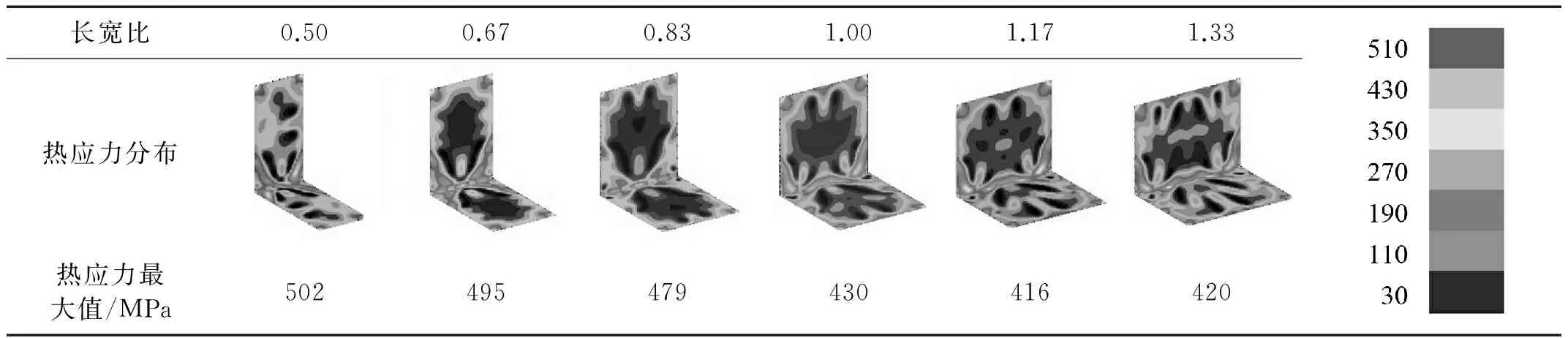
表2 结构热应力

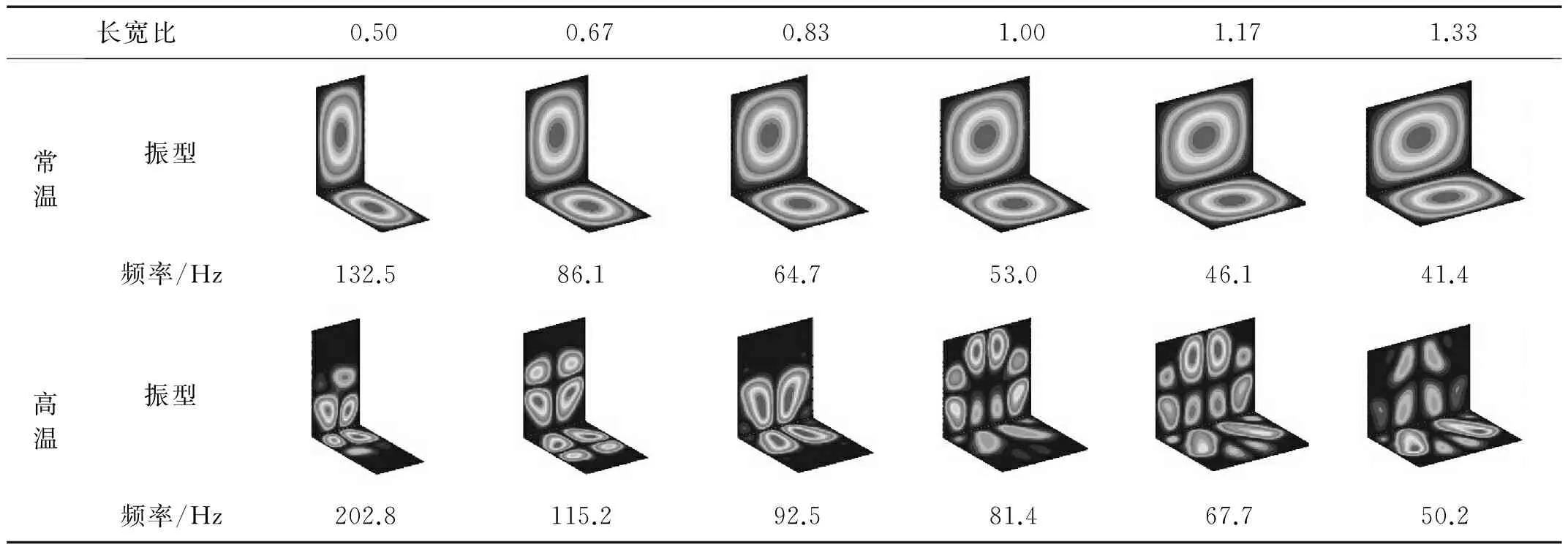
表3 常温和高温环境下结构第一阶模态

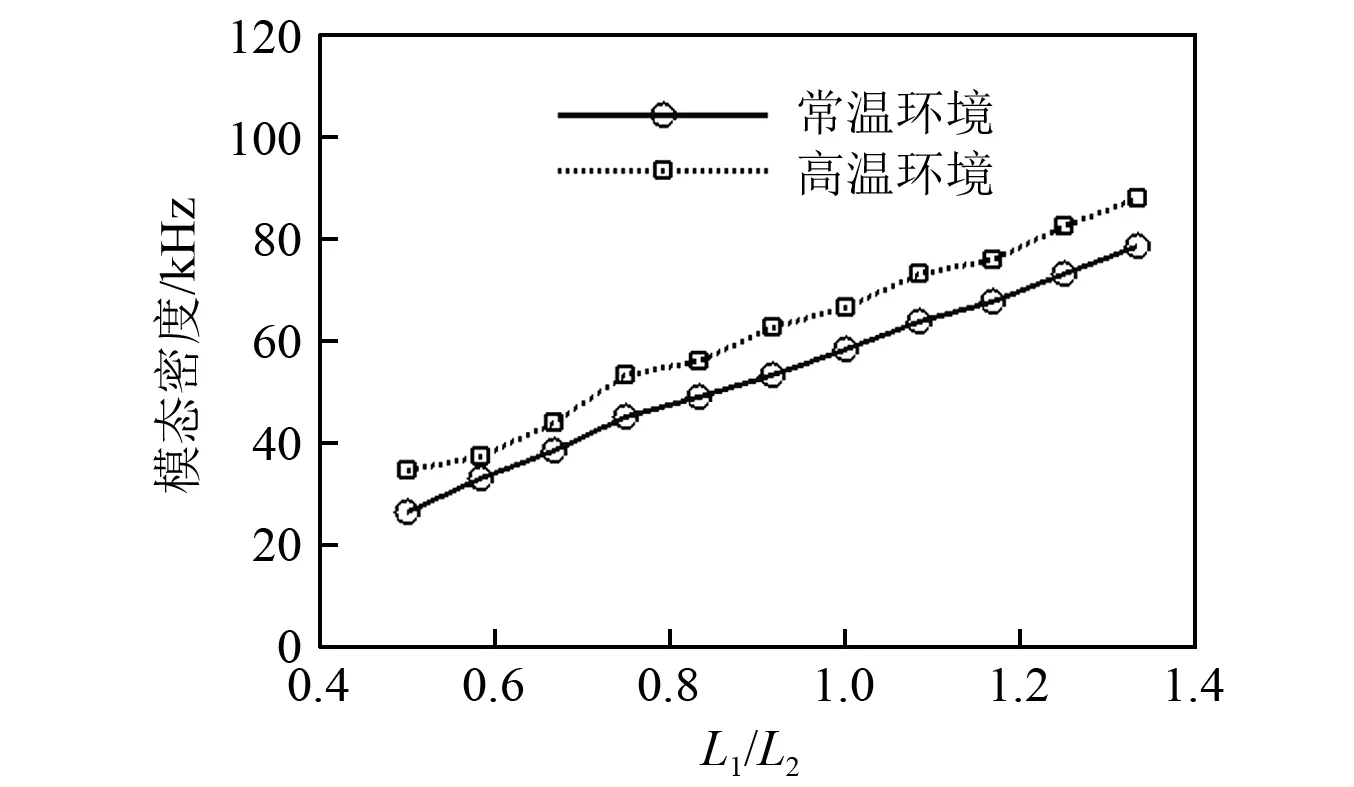
图5 不同长宽比Δω频带内模态密度Fig.5 Modal density in Δω under different aspect ratios

2.4 长宽比对输入功率及振动能量的影响

常温和高温环境下Δω频带内输入功率随长宽比的变化如图6所示。由图6可知常温和高温环境下Δω频带内输入功率随长宽比的变化趋势与模态密度基本一致。由于雨流载荷的假设为各模态的输入功率基本一致，因此相同频段内，模态密度的增多会使得输入功率增大。

常温和高温环境下板1和板2的振动能量如图7所示。计算结果表明：两种环境下，板1和板2的振动能量均随长宽比的增加而逐渐升高，这主要是由于其输入功率的增大。同时，对于相同长宽比的结构，在高温环境下两板的振动能量均高于常温环境，这主要是由于输入功率的增加及模态振型的变化引起的。

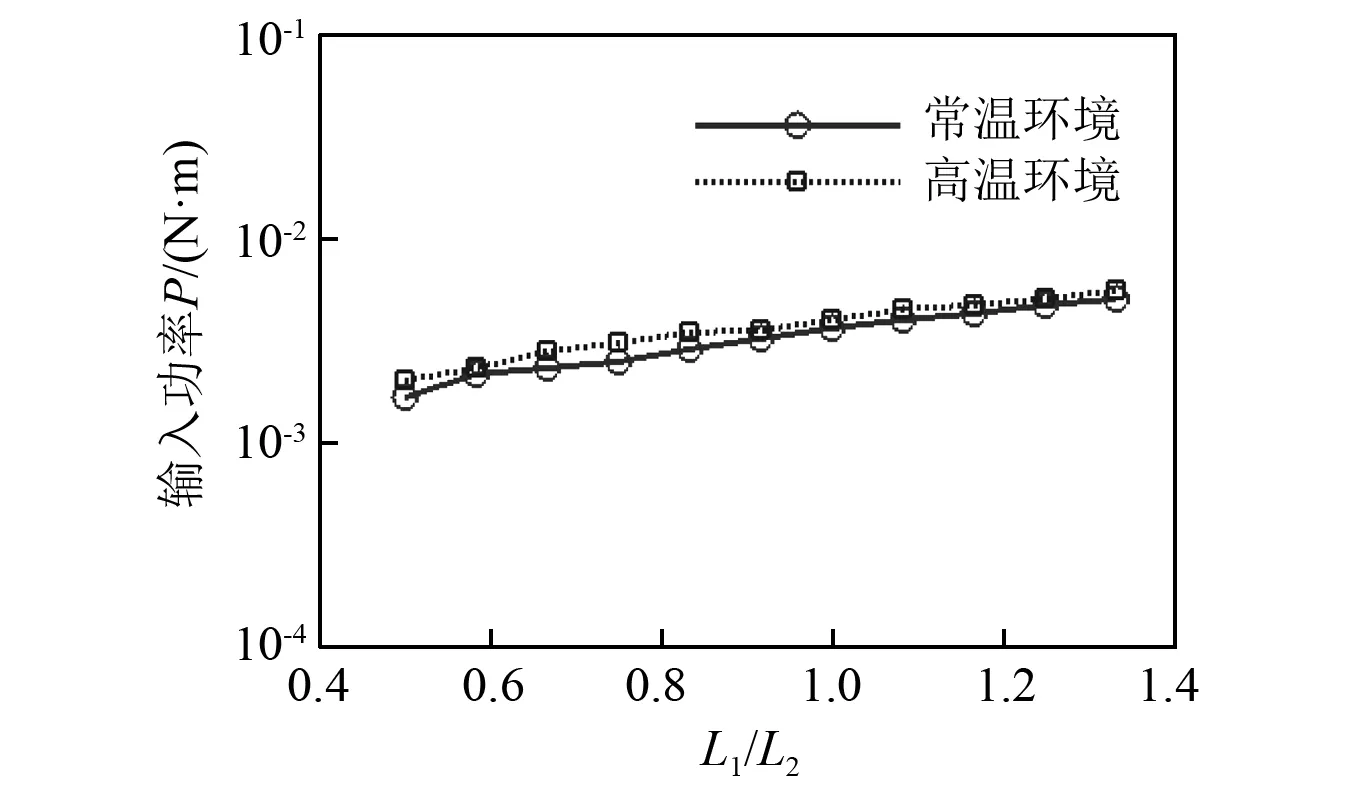
图6 不同长宽比Δω频带内板1上载荷输入功率Fig. 6 Injected power into plate 1 in Δω under different aspect ratios

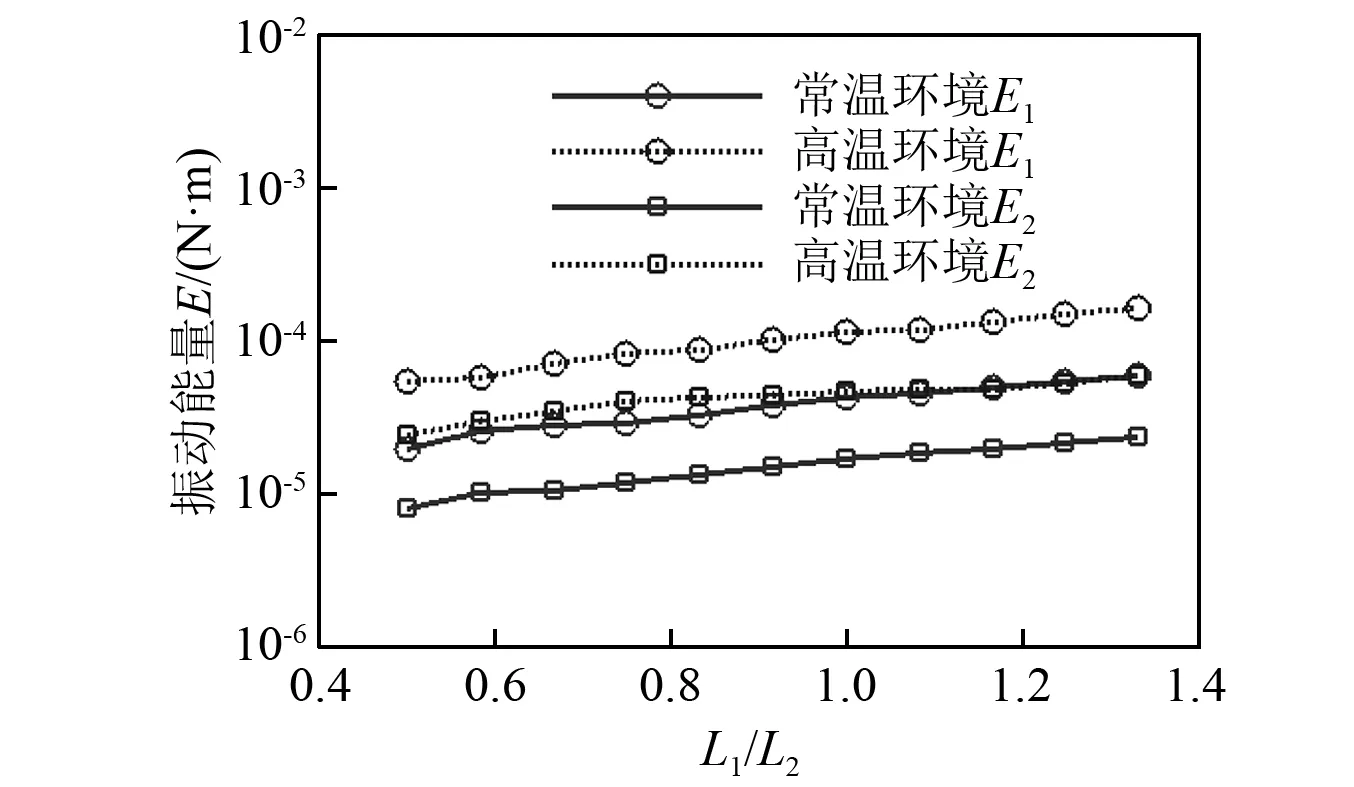
图7 不同长宽比Δω频带内板1和板2的振动能量Fig.7 Vibration energy of plate 1 and plate2 in Δω under different aspect ratios

2.5 长宽比对ILF及CLF的影响

常温和高温环境下Δω频带内随长宽比的变化如图8和图9所示。

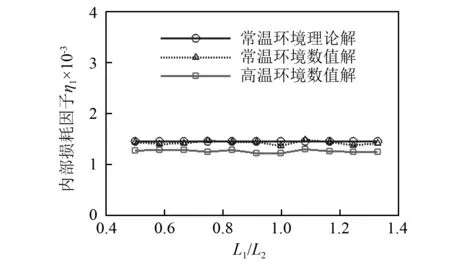
图8 不同长宽比Δω频带内板1上内损耗因子Fig. 8 ILF of plate 1 in Δω under different aspect ratios

图9 不同长宽比Δω频带内板1对板2的耦合损耗因子Fig. 9 CLF of plate 1 to plate 2 in Δω under different aspect ratios

由图8和图9可知，常温环境下的内损耗因子和耦合损耗因子的数值解分别与式(1)和式(2)中的解析解结果基本一致，均与长宽比无关。高温环境下内损耗因子基本未随长宽比的变化而变化，但要低于常温环境，这是由于高温导致两板的振动能量均有较大幅度的升高；长宽比的增加使得结构的耦合损耗因子呈现出先升高后降低的趋势，这主要是由长宽比对子系统振动能量的影响所导致的。

3 结 论

本文基于有限元法和模态坐标系下计及热效应的功率输入法，开展了常温和高温环境下长宽比对L型折板统计能量分析参数的影响研究。首先对比了单位雨流载荷作用下，子系统内损耗因子及子系统间耦合损耗因子的数值解与解析解，验证了数值方法的正确性。随后分析了高温环境下长宽比对结构热应力的影响，开展常温和高温环境下长宽比对L型折板统计能量分析参数的影响研究。结果表明：

(1)常温和高温环境下结构的模态密度均随长宽比的增加而增加，高温环境下模态密度高于常温环境。

(2)常温环境下长宽比的增加对L型折板的内损耗因子及耦合损耗因子影响不大，这与理论解的分析结果一致。

(3)高温环境下长宽比的增加使得L型折板的耦合损耗因子呈现出先升高后降低的趋势，但对内部损耗因子影响不大。同时，其内部损耗因子和耦合损耗因子均低于常温环境。

[ 1 ] BLEVINS R, HOLEHOUSE I, WENTZ K. Thermoacoustic loads and fatigue of hypersonic vehicle skin panels[J]. Journal of Aircraft, 1993, 30(6): 971-978.

[ 2 ] SWANSON A D, COGHLAN S C, PRATT D M, et al. Hypersonic vehicle thermal test challenges[R]. AIAA-2007-1670

[ 3 ] 李彦斌, 张鹏, 吴邵庆, 等. 复合材料加筋板计及热效应的声-固耦合分析[J]. 振动工程学报, 2015, 28(4): 531-540.

LI Yanbin, ZHANG Peng, WU Shaoqing, et al. Structural- acoustic coupling analysis of a composite stiffened panel in a thermal environment[J]. Journal of Vibration Engineering, 2015, 28(4): 531-540.

[ 4 ] JEYARAJ P, GANESAN N, PADMANABHAN C. Vibration and acoustic response of an isotropic plate in a thermal environment[J]. Journal of Vibration and Acoustics, 2008, 130(5): 301-306.

[ 5 ] LYON R H, DEJONG R G. Statistical energy analysis of dynamical systems: theory and applications[M]. Massachusetts: MIT Press, 1975.

[ 6 ] 张婧雯, 孟光, 游进, 等. 基于统计能量法的声场-结构耦合模型高频振动隔振分析[J]. 振动与冲击, 2009, 28(12): 19-22.

ZHANG Jingwen, MENG Guang, YOU Jin, et al. Analysis on high frequency vibration isolation of coupled sound cavity-structure model based on statistical energy method[J]. Journal of Vibration and Shock, 2009, 28(12): 19-22.

[ 7 ] LIMA W D, RAVINDRAN A. Prediction of the cabin noise of business jet using statistical energy analysis[J]. Journal of the Acoustical Society of America, 2010, 127(3): 311-312.

[ 8 ] JI X, CHIN C S. Analysis of acoustic models and statistical energy analysis with direct field for machinery room on offshore platform[J]. Acta Acustica United with Acustica, 2015, 101(6): 1234-1244.

[ 9 ] SWAMINATHAN K, NAVEENKUMAR D T, ZENKOUR A M, et al. Stress, vibration and buckling analyses of FGM plates—A state-of-the-art review[J]. Composite Structures, 2015, 120: 10-31.

[10] PANKAJ A C, SRIDHAR S, MURIGENDRAPPA S M. A compareson of different methods for determination of coupling factor and velocity response of coupled plates[J]. Journal of Vibroengineering, 2013, 15(4):1885-1897.

[11] 江民圣, 牛军川, 郑建华, 等. L 型耦合板结构能量传递系数特性的研究[J]. 振动与冲击, 2015, 34(17): 131-136.

JIANG Minsheng, NIU Junchuan, ZHENG Jianhua, et al. Energy transfer coefficients’ features of L-shaped coupled plates[J]. Journal of Vibration and Shock, 2015, 34(17): 131-136.

[12] BOT A L, COTONI V. Validity diagrams of statistical energy analysis[J]. Journal of Sound and Vibration, 2010, 329(2): 221-235.

[13] 杨雄伟, 李跃明, 闫桂荣. 考虑材料物性热效应飞行器声振耦合动态特性分析[J]. 固体力学学报, 2010, 31(增刊1): 134-142.

YANG Xiongwei, LI Yueming, YAN Guirong. Vibro-acoustic dynamic analysis of aircraft with temperature-dependent material property [J]. Chinese Journal of Solid Mechanics, 2010: 31(Sup 1): 134-142.

[14] 耿谦, 李跃明, 杨雄伟. 热应力作用下结构声-振耦合响应数值分析[J]. 计算力学学报, 2012, 29(1): 99-104.

GENG Qian, LI Yueming, YANG Xiongwei. Vibro-acoustic numerical analysis of thermally stressed aircraft structure [J]. Chinese Journal of Computational Mechanics, 2012, 29(1): 99-104.

[15] 孙树森. 基于统计能量法的潜射导弹振动噪声分析研究[D]. 哈尔滨：哈尔滨工业大学, 2011.

[16] ICHCHOU M N, HIVERNIAU B, TROCLET B. Equivalent ‘rain on the roof’ loads for random spatially correlated excitations in the mid-high frequency range[J]. Journal of Sound and Vibration, 2009, 322(4/5): 926-940.