流固耦合数值方法研究概述与浅析

何 涛

(1.上海师范大学 土木工程系，上海 201418； 2. 英国伯明翰大学 工程学院，伯明翰 B15 2TT)

流固耦合(Fluid-Structure/solid Interaction, FSI)是指浸没在流场中的结构(或固体)受流体激振力发生振动或/和变形、同时结构(或固体)的变化又显著改变流体流动特征而形成的、两介质间无法分割的相互作用。它是自然界的普遍现象，如花瓣随风飘扬、昆虫振翅飞行和水中鱼儿游淌等。连生命体内也不乏各种流固耦合现象，如咽喉呼吸、血管内血液流动及心脏泵送血液等。流固耦合在在工程领域尤为常见，如若忽视其效应或对其考虑不当，极有可能对工程结构造成灾难性后果。以土木工程(结构风工程)为例，超高层建筑、高耸结构、空间结构、大跨桥梁及长径线缆等风敏感结构在强风作用下易产生剧烈振动和/或过大变形。此类结构具有质量轻、柔性大、阻尼小和自振频率低等特点，流固耦合效应突出，风损风毁现象已屡见不鲜。1940年11月7日美国华盛顿州塔科马窄桥建成仅四个月就发生垮塌，如图1(a)所示。究其原因，该桥因气动设计失当导致结构临界风速区间未能避开当时当地风速(约19 m/s，不及设计风速50%)，引发扭转颤振而损毁。2010年12月10日、2011年11月22日和2013年3月9日，属于北京标志建筑的首都机场T3航站楼屋顶局部金属板3次被强风掀开撕裂，内部隔热层材料飘落至停机坪区域和跑道，导致多架次航班延误，如图1(b)所示。这是由于目前对大跨金属屋面风致疲劳及其在强风吸力下传力机制认识不足所致。

这种迥异介质间的相互作用引起科学家和工程师们的强烈兴趣，成为备受瞩目的研究热点。流固耦合蕴含复杂的数学原理和深刻的物理现象[1]。就数学意义说，耦合作用同时对两场控制偏微分方程引入额外的、随时空变化的边界条件，为难点之所在。从物理现象看，钝体受流体激振力、惯性力及弹性力等多重因素耦合作用，会出现涡激振动、驰振、颤振甚至涡激振动与驰振重叠[2-4]，致振机理复杂，对其理解还远未达到成熟。事实上，流固耦合常是一个强非线性问题，影响因素众多且难以分割成流体和固体单独分析，对基础理论、数值方法和实验测试等提出严峻挑战。因此，如何准确考虑流固耦合作用是一个亟待解决的关键问题。还以结构风工程为例，传统手段将风作为外荷载施加在结构上，通过等效静风荷载近似考虑动力效应，取得了一定成效[5-6]。事实上，风与结构的作用是双向耦合的。如果忽略这点，势必与实际情况产生较大偏差。遗憾的是，相关研究目前仍显不足，工程应用零星，更缺乏系统的科学认识。我国相关规范、规程和行业规定等在这方面也无法提供详细有效的条文保障，滞后于工程建设需求。以准稳态风振理论为例，气动参数的获取严重依赖数据输入(由数值计算或实验测试提供)且会因数据误差导致多重值，常用于相对简单情形[7]。当前理论发展与工程实践对流固耦合的认识均不尽如人意。

1 研究概述

流固耦数值模拟既是研究热点，也是研究难点。现有数值方法可分为整体算法、分区算法等常规算法和其它非常规算法(如图2所示)；其中，分区算法可进一步分为显式、隐式和半隐式算法。本文将以任意拉格朗日—欧拉(Arbitrary Lagrangian-Eulerian, ALE)有限元方法为主线、穿插描述其它新方法，介绍流固耦合数值算法的经典研究和近年来的重要进展。

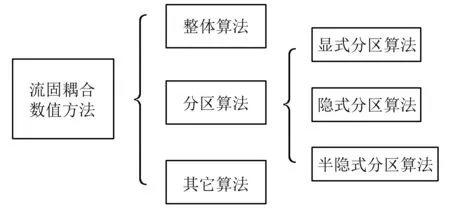
图2 流固耦合数值方法分类Fig.2 Classification of numerical methods for FSI

1.1 国外研究现状

1.1.1 整体算法

从连续介质力学出发，可将流体和固体统一起来，从而发展出了整体算法。整体算法将流体变量和结构变量组装到同一组系统方程中迭代求解，其特殊求解方式导致系统方程规模庞大、刚度矩阵非对称、非线性强。故整体算法丧失了程序模块性和求解灵活性，需较大修改甚至重新编写已有程序。尽管如此，整体算法严格遵守物理守恒、自动满足界面条件、可克服强附加质量效应，引起学者们的浓烈兴趣。Blom[8]较早运用整体算法分析一维活塞问题。稳定性分析表明：隐式求解整体方程令该算法为无条件稳定；阻尼分析表明：该算法无多余能量项，避免计算发散。Hübner等[9]选用速度作为系统变量，借助空时有限元法获得系统的同一空时离散方案，整体求解了几何非线性流固耦合问题，体现出较大挑战性。美国麻省理工学院Bathe[10]领导开发的ADINA软件内置整体求解模块，已用于土木工程、航空航天工程、汽车工程及石油化工等行业。但该软件在几何建模和后处理方面的功能较为单一，有待改善。Liu等[11]基于ALE有限元法提出二阶整体算法，其特色在于构建联合场变量的界面显式推进方案，可适应任意质量比(即结构密度与流体密度之比)。

1.1.2 分区算法

一般认为，流固耦合系统由两场(即流体和结构两个真实物理场)或三场(即两个真实物理场再加上动网格这一虚拟场)方程控制[12]。这就给分区算法提供了施展拳脚的舞台。分区算法顺序交错求解各子问题，可最大限度利用已有程序，灵活选择不同求解器，很好保持了程序模块性，因而应用更广。

显式分区算法无需在每时间步内迭代计算，故具有概念清晰、求解简单和效率高的优点；其缺点是受时间滞后效应影响不满足界面守恒，适合较大质量比情形。Nomura等[13]利用流线迎风彼得洛夫-伽辽金(SUPG)有限元法和预测—多步校正法计算了刚体流固耦合问题，并首次引入一般平面运动协调条件刻画刚体动边界与其重心的几何关系。Wall等[14]开创性设计了方柱后悬臂梁的涡激振动算例，并运用显式分区算法求解。由于结构几何非线性增加求解难度以及充分反映柔性体的复杂流致振动现象，该算例已成为校验耦合算法的基准问题。Jaiman等[15]构建了联合界面边界条件(Combined Interface Boundary Condition, CIBC)方法，结合显式分区算法计算一维活塞问题。该方法的优点为：通过修正界面条件改善显式分区算法的精度和稳定性，大为缓解不利的附加质量效应。通过将火箭模型理想化为刚体，Lefrançois[16]数值模拟了二维膨胀火箭引擎喷嘴的侧向受荷运动，详细分析结构位移、扭转频率及压力变化等振动响应；其中，子块移动技术可避免或减少动网格拟静力方程计算，效率很高。显式分区算法能很好平衡计算精度与效率，是求解大规模气动弹性问题的最佳选择。例如，Belver等[17]直接数值模拟了一90 m钢烟囱的涡激振动，运用分步法结合正交亚格子稳定化技术求解流场、在结构方程中考虑瑞利阻尼效应。需指出，美国斯坦福大学Farhat教授的工作显著推动了显式分区算法发展。Farhat等[18]注意到，结构时间步远大于流体时间步，故可在一个结构时间步内循环计算流体若干次，避免两场同步推进增加计算成本，由此提出了流体子循环概念。Farhat等[19]将流体滞后结构半个时间步形成交错求解，以弥补常规方法违反界面速度连续性的不足，提升了计算精度。

隐式分区算法在每时间步内依次迭代各单场方程直至收敛，虽较为耗时，但满足物理守恒、避免数值失稳。目前固定点法和牛顿法运用最为广泛。Le Tallec等[20]发展了固定点法的预条件最速下降松弛技术。该算法被证明为稳定的能量守恒方案，用于求解复杂工业问题。Küttler等[21]根据界面位移构造动态松弛因子，提出了基于Aitken’s Δ2加速技术的固定点迭代法，数值模拟了柔性体流固耦合问题。特别指出，Le Tallec等为研究固定点法的重要工作，广为引用。Wang等[22]基于梯度光滑技术分析了几何非线性流固耦合问题，即采用边界光滑有限元求解固体、梯度光滑有限差分法求解流场。由于流体速度和压力不可显式解耦，梯度光滑概念难以用于流体有限元计算，Wang等则通过有限差分法化解该难题。牛顿法可克服固定点法收敛缓慢的缺点，受到较多青睐。Dettmer等[23]提出牛顿—拉普森隐式耦合方法，残差收敛分析表明该算法为二次收敛。Degroote[24]建议了界面准牛顿算法，可近似求解雅可比矩阵及其逆矩阵，收敛率较高。

半隐式分区算法是近年出现的第三类分区算法，求解过程分为显式耦合和隐式耦合两步，主要优势为：稳定性与隐式分区算法相当，但效率更胜一筹。Fernández等[25]借助映射分离提出了半隐式算法，具体措施为：先显式处理ALE对流—扩散项与网格运动以提高计算效率，然后在固定网格上隐式耦合压力项与结构运动以确保稳定性。Breuer等[26]基于商业软件独立设计了一种分区半隐式预测—校正法，结合大涡模拟和非匹配网格模拟了圆柱后弹性悬臂梁的涡激振动问题。与Fernández等的研究不同，流体动量方程以整体方式求解，故在显式步中仅含网格运动。随后，Murea等[27]在界面处构造最小二乘问题实现连续性条件，利用BFGS迭代法求解相应优化问题并研究了算法稳定性。文献[27]的基本框架与文献[26]保持一致。半隐式分区算法在血液动力学中通过出口/入口压力条件实现半隐式耦合，目前尚难以用于计算结构风工程问题。笔者针对半隐式分区算法的不足进行了研究，取得了一定成果，详见后文。

1.2 国内研究现状

近年来，国内学者越来越关注流固耦合问题，研究热情持续高涨，涌现出较多高水平成果，成绩不俗。哈尔滨工业大学沈世钊等[28]运用显式分区算法分析了二维柔性膜结构与风耦合作用，并对比了不考虑流固耦合作用的结果。在文献[28]中，流场求解基于泰勒—伽辽金方法，湍流计算使用Smagorinsky大涡模拟。同济大学顾明等[29]提出“模态耦合因子”新概念，运用随机振动理论近似求解风载下结构的共振响应耦合模态，并用于分析铁路上海南站大跨屋顶风效应。昆明理工大学张立祥等[30]基于隐式分区算法和大涡模拟数值计算了三维涡轮机叶片的流固耦合效应，其特色之处在于运用了预测—多步校正法和Newmark方法分别预测流体和固体，然后进行双修正。大连理工大学孙东科、林家浩课题组基于商业软件实施隐式迭代，并选用k-ω湍流模型数值模拟了二维机翼颤振问题[31]。辽宁工程技术大学孙芳锦与同济大学顾明合作进行基于ANSYS软件二次开发的流固耦合研究，运用整体算法数值模拟了柔性膜结构风振耦合作用[32]。西安交通大学张家忠课题组数值模拟了二维局部柔性机翼的流固耦合，采用简化梁挠度方程考虑结构局部大变形[33]。上海交通大学周岱课题组利用显式分区算法数值模拟了双柱体尾激振动，揭示了相应流致振动现象及作用机理[34]。葛耀君[35]课题组基于风洞实验数据研究提出风载下柔性结构的尾流振子模型，具有较强工程意义。华南理工大学魏德敏等[36]考虑不同来风特性研究了索穹顶结构风振响应。湖南大学陈政清[37]课题组基于ANSYS软件研究了安装亮化灯具导致的斜拉桥拉索风致驰振作用，将模型简化为相对来流有一定攻角的三圆柱串列模型，分析了不同风速对桥梁结构及拉索的影响。浙江大学楼文娟[38]课题组根据三角形重心坐标系原理提出基于显式耦合计算的流固耦合网格协调插值新方法，数值模拟了柔性平屋盖结构风振响应，分析了气动阻尼效应。天津大学及春宁等[39]模拟了层流下串列低质量比双圆柱的涡激振动，讨论了2种工况和不同间距比，基于流致振动现象给出耦合机理解释。

此外，清华大学、北京大学、香港大学、中科院力学所等众多单位从不同角度研究了流固耦合问题，在此不再赘述。

1.3 基于CBS方法的流固耦合研究

特征线分裂(Characteristic-Based Split, CBS)技术是一种通用的计算流体动力学数值方法，应用较为广泛[40-41]。笔者运用ALE-CBS有限元法进行了一系列流固耦合数值方法研究，包括：

(1)构建了混合型界面耦合条件，并不断完善其理论。针对CIBC公式中存在结构应力项、不能用于刚体流固耦合和无法反映完整流体应力张量的不足，提出了改进CIBC方法[42-48]。

(2)发展了单场单体求解的优化方法，并结合改进CIBC方法，分别建立了显式、隐式和半隐式分区耦合算法[42-53]。

(3)数值模拟了各类典型几何截面钝体的流致振动，揭示了振动钝体的响应规律和特征现象[54-59]。

有关CIBC方法的最新研究进展，读者可参阅最新综述论文，见文献[60]。

2 发展趋势

随着计算力学理论和计算机技术的发展，流固耦合计算新方法不断被提出，呈现百花齐放、百家争鸣的总体发展趋势，其实质反映了数值研究不断追求“高精度、高效率与稳定性”的永恒目标，主要体现在：

(1)ALE方法继续占据主流，其它新概念将有较大发展。ALE描述统一了拉格朗日描述和欧拉描述，克服了各自缺点：既能追踪动边界，又可避免网格畸变。借助ALE描述，基于网格的空间离散方法可方便求解流固耦合且相当有效。随着研究不断深入、其它技术短期内难有重大突破，ALE方法将继续成为数值分析流固耦合的主流手段。得益于理论进步，一批新方法同时将有较大飞跃。以浸透边界元法[61]为例，该方法早期缺点(如核函数插值导致精度下降、计算刚体困难及耦合施力不一致等)一一被解决或改进。“浸透”概念还显著推动其它欧拉型方法的快速发展，带动新研究热潮。

(2)提出统一公式整体算法，避免繁杂非线性迭代。常规整体算法寻求特殊的非线性方程线性化解法，计算精度与效率大打折扣。如能将流体和固体嵌入单一介质框架内，便可对二者采用相同变量与求解方案(即单一网格划分、空间离散、时间推进方案和迭代技术)，协调性好，数学处理容易。例如，Papadakis[62]采用速度和压力作为变量，对流体和固体构造形式相同的控制方程和本构关系，提出统一迭代求解方案。然而，这类研究目前尚不多见。

(3)发展精确、高效分区算法，发挥既有方法优势。具体体现在：①耦合先进单场技术。分区算法可最大限度保持程序模块性，故耦合各种先进单场求解技术是自然选择。譬如，Navier-Stokes方程的稳定化解法、精确的固体光滑有限元方法、简单高效的网格更新技术等改进措施；构造新型界面耦合条件；灵活使用非匹配网格；耦合不同空间离散方法；等等。②稳定化显式分区算法。显式分区算法的效率优势突出，但遇结构较柔或强附加质量效应时会出现数值失稳。发展稳定化显式耦合技术，发挥高效优势、适应强附加质量效应，是今后研究的重要发展方向。当前仅在血液动力学流固耦合分析中有少量应用[63]。③高效(半)隐式分区算法。(半)隐式分区算法迭代求解耗时。研究关键在于能否提出高效、高精度的迭代耦合算法。成功例子有Atiken方法和准牛顿法等。

3 目前存在的问题及解决途径

由前文可知，当前流固耦合数值方法研究还存在以下不足：

(1)数值理论方面，包括：①传统观点认为单场交错求解导致分区计算中的时间滞后效应，主要注重场方程求解，忽略了时变边值延滞同时恶化两场方程解的本质；②连续介质物理律及本构关系在公式表达上具有高度一致性，当前还未充分利用这一特点开发更灵活的整体求解策略；③对实际湍流考虑不多且多受限于商业软件。这些问题直接影响流固耦合计算的精度、效率和适用范围。

(2)工程应用方面，包括：①数值研究较少涉及土木工程风敏感结构，且在既有应用中多关注(二维)外形简单的刚体或线弹性体，对(三维)超弹性柔性体、多钝体群(尤其是刚-柔、柔-柔体系)研究不多；②实际工程多采用准定常方法将耦合效应简化为拟动力作用，较少运用计算力学手段，难以精准确定全时程耦合作用；③片面强调风的复杂性或仅关注结构响应，对流致振动现象本质与机理认识不清、诠释不足。

针对以上问题，可能解决途径有：①理论方面，包括从数学理论与物理原理出发，大力发展新型/混合型流-固交界面条件、提出反映复杂历史时程的预测措施、构筑精确与稳定的流体求解器、基于连续介质力学的统一本构方程等；②实践方面，针对复杂形体的简化工程计算方法、考虑结构-强风充分耦合、在相关设计规范中引入更合理条款、加强风洞与水槽实验技术研究、基于流动现象与振动响应的耦合机理深入研究等。

4 结 语

本文简要评述与分析了流固耦合数值方法的研究进展及各自特点，讨论了早期经典文献与近年最新研究成果。流固耦合问题属多学科交叉研究，难度较大，研究成果远未成熟。当前理论研究与应用虽有较快发展，但还需持续不断深化。基于计算力学发展更为精确、高效和稳定的数值模拟技术，模拟复杂实际情况(如湍流、结构疲劳等)的流固耦合问题，并推进并行计算技术(如GPU辅助加速并行运算、云计算等)的深入应用，将是未来重要的研究方向。

[ 1 ] ZHANG J, CHILDRESS S, LIBCHABER A, et al. Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind[J]. Nature, 2000, 408(6814): 835-839.

[ 2 ] BEARMAN P W. Vortex shedding from oscillating bluff bodies[J]. Annual Review of Fluid Mechanics, 1984, 16(1): 195-222.

[ 3 ] PARKINSON G. Phenomena and modelling of flow-induced vibrations of bluff bodies[J]. Progress in Aerospace Sciences, 1989, 26(2): 169-224.

[ 4 ] WILLIAMSON C H K, GOVARDHAN R. Vortex-induced vibrations[J]. Annual Review of Fluid Mechanics, 2004, 36(1): 413-455.

[ 5 ] 卢春玲, 李秋胜, 黄生洪, 等. 深圳平安国际金融大厦风致响应大涡模拟分析[J]. 建筑结构学报, 2012, 33(11): 1-11.

LU Chunling, LI Qiusheng, HUANG Shenghong, et al. Large eddy simulation of wind induced response on the Shenzhen Pingan IFC Building[J]. Journal of Building Structures, 2012, 33(11): 1-11.

[ 6 ] 李玉学, 杨庆山, 田玉基, 等. 大跨屋盖结构多目标等效静力风荷载[J]. 工程力学, 2016, 33(6): 85-92.

LI Yuxue, YANG Qingshan, TIAN Yuji, et al. Multiple targets equivalent static wind load for long-span roofs[J]. Engineering Mechanics, 2016, 33(6): 85-92.

[ 7 ] JOLY A, ETIENNE S, PELLETIER D. Galloping of square cylinders in cross-flow at low Reynolds numbers[J]. Journal of Fluids and Structures, 2012, 28: 232-243.

[ 8 ] BLOM F J. A monolithical fluid-structure interaction algorithm applied to the piston problem[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 167(3/4): 369-391.

[ 9 ] HÜBNER B, WALHORN E, DINKLER D. A monolithic approach to fluid-structure interaction using space-time finite elements[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(23): 2087-2104.

[10] BATHE K J, LEDEZMA G A. Benchmark problems for incompressible fluid flows with structural interactions[J]. Computers & Structures, 2007, 85(11/12/13/14): 628-644.

[11] LIU J, JAIMAN R K, GURUGUBELLI P S. A stable second-order scheme for fluid-structure interaction with strong added-mass effects[J]. Journal of Computational Physics, 2014, 270: 687-710.

[12] FARHAT C. Application of a three-field nonlinear fluid-structure formulation to the prediction of the aeroelastic parameters of an F-16 fighter[J]. Computers & Fluids, 2003, 32: 3-29.

[13] NOMURA T, HUGHES T J R. An arbitrary lagrangian-eulerian finite element method for interaction of fluid and a rigid body[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 95(1): 115-138.

[14] WALL W A, RAMM E. Fluid-structure interaction based upon a stabilized (ALE) finite element method[C]∥ Proceedings of the 4th World Congress on Computational Mechanics: New Trends and Applications, Idelsohn SR, Oate E and Dvorkin EN (eds), CIMNE, Barcelona, Spain, 1998: 1-20.

[15] JAIMAN R, GEUBELLE P, LOTH E, et al. Combined interface boundary condition method for unsteady fluid-structure interaction[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200: 27-39.

[16] LEFRANCOIS E. A numerical investigation of side-loads resulting from rigid body motions of an overexpanded engine nozzle[J]. International Journal for Numerical Methods in Fluids, 2011, 66(6): 671-689.

[17] BELVER A V, IBN A L, LAVN MARTN C E. Coupling between structural and fluid dynamic problems applied to vortex shedding in a 90 m steel chimney[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 100(1): 30-37.

[18] FARHAT C, LESOINNE M, MAMAN N. Mixed explicit/implicit time integration of coupled aeroelastic problems: Three-field formulation, geometric conservation and distributed solution[J]. International Journal for Numerical Methods in Fluids, 1995, 21(10): 807-835.

[19] FARHAT C, LESOINNE M. Two efficient staggered algorithms for the serial and parallel solution of three-dimensional nonlinear transient aeroelastic problems[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 182(3/4): 499-515.

[20] LE TALLEC P, MOURO J. Fluid structure interaction with large structural displacements[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(24/25): 3039-3067.

[21] KÜTTLER U, WALL W. Fixed-point fluid-structure interaction solvers with dynamic relaxation[J]. Computational Mechanics, 2008, 43(1): 61-72.

[22] WANG S, KHOO B C, LIU G R, et al. Coupling GSM/ALE with ES-FEM-T3 for fluid-deformable structure interactions[J]. Journal of Computational Physics, 2014, 276: 315-340.

[24] DEGROOTE J. Partitioned simulation of fluid-structure interaction: Coupling black-box solvers with quasi-Newton techniques[J]. Archives of Computational Methods in Engineering, 2013, 20(3): 185-238.

[26] BREUER M, DE NAYER G, MÜNSCH M, et al. Fluid-structure interaction using a partitioned semi-implicit predictor-corrector coupling scheme for the application of large-eddy simulation[J]. Journal of Fluids and Structures, 2012, 29: 107-130.

[27] MUREA C M, SY S. A fast method for solving fluid-structure interaction problems numerically[J]. International Journal for Numerical Methods in Fluids, 2009, 60(10): 1149-1172.

[28] WU Y, SUN X, SHEN S. Computation of wind-structure interaction on tension structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10): 2019-2032.

[29] GU M, ZHOU X Y. An approximation method for resonant response with coupling modes of structures under wind action[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(11/12): 573-580.

[30] ZHANG L, GUO Y, WANG W. FEM simulation of turbulent flow in a turbine blade passage with dynamical fluid-structure interaction[J]. International Journal for Numerical Methods in Fluids, 2009, 61(12): 1299-1330.

[31] BAI Y, SUN D, LIN J, et al. Numerical aerodynamic simulations of a NACA airfoil using CFD with block-iterative coupling and turbulence modeling[J]. International Journal of Computational Fluid Dynamics, 2012, 26(2): 119-132.

[32] SUN F J, GU M. A numerical solution to fluid-structure interaction of membrane structures under wind action[J]. Wind & Structures, 2014, 19(1): 35-58.

[33] KANG W, ZHANG J, LEI P, et al. Computation of unsteady viscous flow around a locally flexible airfoil at low Reynolds number[J]. Journal of Fluids and Structures, 2014, 46: 42-58.

[34] HAN Z, ZHOU D, TU J. Wake-induced vibrations of a circular cylinder behind a stationary square cylinder using a semi-implicit characteristic-based split scheme[J]. Journal of Engineering Mechanics-ASCE, 2014, 04014059.

[35] XU K, GE Y J, ZHANG D C. Wake oscillator model for assessment of vortex-induced vibration of flexible structures under wind action[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 136: 192-200.

[36] 魏德敏, 徐牧, 李頔. 索穹顶结构风振响应时程分析[J]. 振动与冲击, 2013, 32(17): 68-73.

WEI Demin, XU Mu, LI Di. Time-history analysis of wind-induced vibration response for a cable dome structure[J]. Journal of Vibration and Shock, 2013, 32(17): 68-73.

[37] 董国朝, 陈政清, 罗建辉, 等. 安装亮化灯具导致的斜拉桥拉索风致驰振流固耦合分析[J]. 中国公路学报 2012, 25(1): 67-75.

DONG Guochao, CHEN Zhengqing, LUO Jianhui et al. Fluid-structure interaction analysis of wind-induced galloping of cables with lamps of cable-stayed bridge[J]. China Journal of Highway and Transport, 2012, 25(1): 67-75.

[38] 卢旦, 楼文娟, 杨毅. 索膜结构风致流固耦合气动阻尼效应研究[J]. 振动与冲击, 2013, 32(6): 47-53.

LU Dan, LOU Wenjuan, YANG Yi. Numerical calculation on wind-induced damping of membrane structure based on fluid-structure interaction[J]. Journal of Vibration and Shock, 2013, 32(6): 47-53.

[39] 及春宁, 陈威霖, 黄继露, 等. 串列双圆柱流致振动的数值模拟及其耦合机制[J]. 力学学报, 2014, 46(6): 862-870.

JI Chunning, CHEN Weilin, HUANG Jilu, et al. Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanisms[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 862-870.

[40] ZIENKIEWICZ O C, NITHIARASU P, CODINA R, et al. The characteristic based split procedure; An efficient and accurate algorithm for fluid problems[J]. International Journal for Numerical Methods in Fluids, 1999, 31: 359-392.

[41] NITHIARASU P, CODINA R, ZIENKIEWICZ O C. The Characteristic-Based Split (CBS) scheme—a unified approach to fluid dynamics[J]. International Journal for Numerical Methods in Engineering, 2006, 66: 1514-1546.

[42] 周岱, 何涛, 李俊龙. 一种改进弱耦合分区迭代算法及在流固耦合问题中的应用[C]∥第十五届结构全国风工程学术会议, 浙江大学, 杭州, 2011: 142-145.

[43] 周岱, 何涛, 涂佳黄. 流固耦合分析的一种改进CBS有限元算法[J]. 力学学报, 2012, 44(3): 494-504.

ZHOU Dai, HE Tao, TU Jiahuang. A modified CBS finite element method approach for fluid-structure interaction[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(3): 494-504.

[44] HE T, ZHOU D, BAO Y. Combined interface boundary condition method for fluid-rigid body interaction[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 223/224: 81-102.

[45] HE T, ZHOU D, HAN Z, et al. Partitioned subiterative coupling schemes for aeroelasticity using combined interface boundary condition method[J]. International Journal of Computational Fluid Dynamics, 2014, 28: 272-300.

[46] HE T. A partitioned implicit coupling strategy for incompressible flow past an oscillating cylinder[J]. International Journal of Computational Methods, 2015, 12(3): 1550012.

[47] HE T. A CBS-based partitioned semi-implicit coupling algorithm for fluid-structure interaction using MCIBC method[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 298: 252-278.

[48] He T, ZHANG K. Combined interface boundary condition method for fluid-structure interaction: Some improvements and extensions[J]. Ocean Engineering, 2015, 109: 243-255.

[49] HE T. Partitioned coupling strategies for fluid-structure interaction with large displacement: Explicit, implicit and semi-implicit schemes[J]. Wind & Structures, 2015, 20(3): 423-448.

[50] HE T. On a partitioned strong coupling algorithm for modeling fluid-structure interaction[J]. International Journal of Applied Mechanics, 2015, 7(2): 1550021.

[51] HE T. Semi-implicit coupling of CS-FEM and FEM for the interaction between a geometrically nonlinear solid and an incompressible fluid[J]. International Journal of Computational Methods, 2015, 12(5): 1550025.

[52] 何涛. 一种求解流固耦合问题的强耦合算法[C]∥. 第十七届全国结构风工程学术会议, 武汉大学, 武汉, 2015: 14-19.

[53] HE T, ZHANG K, WANG T. AC-CBS-based partitioned semi-implicit coupling algorithm for fluid-structure interaction using stabilized second-order pressure scheme [J]. Communications in Computational Physics, 2017, 21(5): 1449-1474.

[54] 何涛. 流固耦合新算法研究及其气动弹性应用[D]. 上海: 上海交通大学, 2013.

[55] 周岱, 何涛, 刘光众. 基于改进CIBC方法的方柱驰振预测[J]. 水动力学研究与进展A辑, 2013, 28(4): 391-398.

ZHOU Dai, HE Tao, LIU Guangzhong. Rotational galloping prediction of a rectangular cylinder using the CIBC method[J]. Chinese Journal of Hydrodynamics, 2013, 28(4): 391-398.

[56] 马晋, 周岱, 何涛. 基于CIBC迭代耦合技术的矩形柱扭转驰振分析[J]. 建筑科学与工程学报, 2013, 30(2): 70-75.

MA Jin, ZHOU Dai, HE Tao. Analysis of a rotationally oscillating rectangular cylinder using CIBC method [J]. Journal of Architecture and Civil Engineering, 2013, 30(2):70-75.

[57] HE,T Han Z, Zhou D. Fluid-rigid body interaction using a modified combined interface boundary condition method[C]∥Proceedings of the 1st National Symposium on Spatial Structures for Doctoral Candidates of China, Zhejiang University, Hangzhou, China, 2012: 204-217.

[58] HE T, ZHOU D. VIV of a flexible circular cylinder based on the CIBC method[C]∥Proceedings of the 7th International Colloquium on Bluff Body Aerodynamics and Applications (BBAA7), Shanghai, China, 2012: 601-609.

[59] ZHOU D, MA J, HE T. Analysis of transient fluid-flexible body interaction based on a CBS-based partitioned semi-implicit coupling scheme[C]∥Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium—“Shells, Membranes and Spatial Structures Footprints”, September 15-19, 2014, the Polytechnic School of the University of São Paulo, Brazil.

[60] HE T, ZHANG K. An overview of the combined interface boundary condition method for fluid-structure interaction[J]. Archives of Computational Methods in Engineering, 2017, 24(4): 891-934.

[61] PESKIN C S. The immersed boundary method[J]. Acta Numerica, 2002, 11: 479-517.

[62] PAPADAKIS G. A novel pressure-velocity formulation and solution method for fluid-structure interaction problems[J]. Journal of Computational Physics, 2008, 227(6): 3383-3404.

[63] BURMAN E, FERNáNDEZ M A. Explicit strategies for incompressible fluid-structure interaction problems: Nitsche type mortaring versus Robin-Robin coupling[J]. International Journal for Numerical Methods in Engineering, 2014, 97(10): 739-758.