基于迭代广义解调算法的变转速滚动轴承复合故障特征的提取

赵德尊， 李建勇, 2， 程卫东， 温伟刚

(1.北京交通大学 机械与电子控制工程学院，北京 100044; 2.载运工具先进制造与测控技术教育部重点实验室, 北京 100044)

滚动轴承是旋转机械中的重要部件，由于复杂的工作环境(高温、重载)及运行状态(急剧变转速、变负载)，滚动轴承也是旋转机械中最易受损的零部件之一。据有关资料统计：在使用滚动轴承的旋转机械中有超过30%的机械故障是故障轴承引起的[1]，而且实际工况中，故障点往往不止一处，某些故障常常会诱发其位置的故障发生，进而出现多个故障并存的状态[2]。另外，变转速模式普遍存在于旋转机械的实际运行中[3-4]。该条件下，由故障引起的冲击间隔将随转速变化发生改变，使得频率谱中出现频率模糊现象，无法有效的完成故障特征的识别。因此，对变转速条件下滚动轴承复合故障特征提取的研究具有重要的意义。

近年来，许多学者致力于滚动轴承复合故障提取的研究，并取得了很多成果。明安波等[5]将小波分解与频谱自相关相结合，通过对单通滚动轴承道复合故障信号的分解，有效的实现了相互交错、叠加在同一频带的内、外圈故障特征的分离和提取。马新娜等[6]将EMD算法与自适应陷波器系统相结合在一定程度上满足了滚动轴承复合故障信号分离和故障诊断的要求。Chen等[7]提出了基于改进的自适应沉余提升多小波和希尔伯特解调方法相结合的滚动轴承复合故障特征提取方法。仿真和实验对比结果表明了该算法相对于传统算法的优越性；Zhang等[8]则提出了基于伪时频分析与Dopplerlet滤波器相结合的滚动轴承道旁声音信号复合故障特征提取方法。该方法可以有效的利用道旁声音信号实现滚动轴承的复合故障诊断。然而上述方法都受制于转速恒定或小范围波动这一前提条件，对于转速大范围变化的故障轴承信号无能为力。

针对变转速工作模式对故障轴承信号产生的影响，计算阶比分析是公认的最为有效的算法[9-10]。该算法的核心是获得相对于参考轴的恒定角增量采样，将时域的非周期信号转化为角域周期信号以消除转速变化对振动信号的影响。然而，如果利用计算阶比分析算法对复合故障轴承信号进行处理，由于复合故障相互干扰、彼此叠加，将使得包络阶比谱中代表故障特征的峰并不突出以及具有较多的干扰成分，因此容易出现漏判或误判。另外，阶比分析方法存在理论上的缺陷，即重采样过程中大量二次或高次方程的求解使得计算效率较低[11]，以及包络畸变等原因容易产生误差[12]，进而影响故障诊断的结果。因此有必要提出新的方法以消除变转速工作模式对故障轴承振动信号的影响。

广义解调算法是Olhede等[13]提出的一种可以将时频分布是倾斜非平稳的信号转换成时频分布是线性的且平行于时间轴的平稳信号的一种分析方法，并将其成功的应用于语音信号。近年来，基于广义解调算法适用于调幅-调频信号的特点，许多学者将其应用于机械设备的故障诊断[14-16]。然而，广义解调算法只能对信号时频谱中的单一曲线进行识别与重置，难以处理时频图中含有非平行多曲线的多分量信号。因此有学者对广义解调算法进行了改进和优化，提出了迭代广义解调算法，并将其用于行星齿轮箱的故障诊断[17-18]。

综上所述，本文提出了基于迭代广义解调算法的变转速滚动轴承复合故障特征提取方法。该方法的核心是利用迭代广义解调算法将复合故障轴承信号的包络时频谱中与故障特征有关的多条特定时频成分转换成平行于时间轴的直线，使其满足快速傅里叶变换的要求，进而通过识别频率谱中突出峰的位置确定目标轴承的故障数量及故障位置。基于迭代广义解调算法的变转速滚动轴承复合故障特征提取方法的优点主要包括以下两个方面：首先，舍弃计算阶比分析方法，直接通过迭代广义解调算法消除转速变化对滚动轴承故障特征的影响，为变转速条件下滚动轴承复合故障特征的提取提供了新思路；其次，该方法通过相位函数只对故障轴承信号中的特定成分进行分析，使得频谱中不存在明显的峰值干扰，易于故障特征的提取和故障点位置的判别。

1 算法部分

1.1 复合故障轴承信号的时频特性

当轴承某一位置出现表面损伤类故障时，故障点与其对应的配合表面之间因为碰撞会在相应的振动信号中产生一个高幅值并且快速衰减的冲击。随着滚动轴承的不断运行，上述冲击将会以固定的时间间隔重复出现，其对应的重复频率即为故障特征频率。故障特征频率公式可参考文献[10]。根据故障特征频率计算公式得知滚动轴承内、外圈及滚动体对应的故障特征频率与轴承转频具有固定的比例关系且只与目标轴承几何参数有关。将该比例关系定义为故障特征系数，其公式形式如下：

Fo=fo/fr

(1)

Fi=fi/fr

(2)

Fb=fb/fr

(3)

式中：Fo、Fi和Fb分别表示目标轴承内圈、外圈及滚珠故障时对应的故障特征系数;fo、fi和fb分别表示目标轴承的外圈、内圈及滚珠故障时对应的故障特征频率；fr为目标轴承转频。

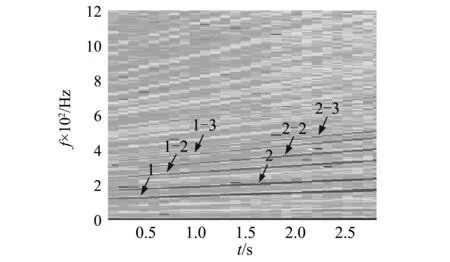
图1 复合故障轴承仿真信号的包络时频图Fig.1 Envelope time-frequency representation of the multi-fault bearing signal

故障点与其对应的配合表面之间因碰撞而产生的故障冲击将进一步引起机械结构的高频共振。因此，故障轴承振动信号可以看作以机械结构的共振频率为载频以故障特征系数为调频的幅值解调信号。利用Hilbert变换对故障轴承振动信号进行解调，解调信号的时频谱中将会出现成特定规律变化的时频曲线。上述时频曲线即为故障特征频率趋势线及其倍频。当轴承出现多个故障时，其包络信号的时频图中同样出现多组故障特征频率趋势线及其倍频，如图1所示(信号为仿真信号，具体参数见仿真部分)。图中1和2分别表示故障点1和故障点2所对应的故障特征频率趋势线，1-2、1-3以及2-2，2-3分别表示两处故障点故障特征频率的谐波。由于转速曲线成线性变化，根据公式(1)～(3)，故障特征频率也以同样的变化趋势成线性变化。这也是造成以快速傅里叶变换为核心的频谱分析方法失效，产生频率模糊现象的原因。

根据以上分析，如果能够利用转频信息以及目标轴承的故障特征系数对其包络时频图中的故障特征频率进行识别和重置，使其成为平行与时间轴的直线，即可利用频谱分析对故障特征频率进行提取和识别。进而确定目标轴承的故障数量以及类型。

1.2 迭代广义解调算法

广义解调可以通过预设的相位函数把信号时频分布中的特定曲线成分转换成线性的、平行于时间轴的直线。其本质为广义傅里叶变换。对于任意单分量信号x(t)，其广义傅里叶变换的定义为：

(4)

式中：s0(t)表示随时间t变化的实值函数，实际上是对x(t)e-2jπs0 (t )做标准的傅里叶变换。

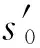
实际工况中，多分量信号普遍存在于旋转机械中。而原始广义解调算法只能对原始信号中的单一分量进行单次解调。为有效的解调多分量信号中的多个特定成分，有学者对广义解调进行了优化，提出了迭代广义解调算法。迭代广义解调算法的核心通过改变预设的相位函数，对原始信号进行反复的广义解调。其具体步骤如下：

(1)通过传统的时频分析方法如短时傅里叶变换确定原始信号x(t)中的特定时频成分；

(2)利用数据拟合算法估计原始信号中每一成分xi(t)的瞬时频率fi(t)；

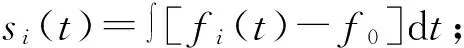
(4)对原始信号x(t)进行Hilbert变换，获得解析信号y(t)=x(t)+jH[x(t)]，其中H[x(t)]是x(t)的Hilbert变换；

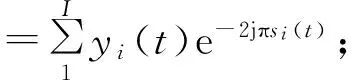
(6)对解调信号d(t)进行Hilbert变换得到新的解析信号z(t)=d(t)+jH[d(t)]，其中H[d(t)]是d(t)的Hilbert变换。

1.3 算法流程图

变转速条件下，滚动轴承复合故障信号的包络时频图中存在成规律分布且能够代表轴承故障特征的时频曲线。上述时频曲线与转频之间有固定的比例关系，比例系数即为故障特征系数。因此本文利用故障轴承信号的同步转频信息以及目标轴承的故障特征系数确定迭代广义解调算法所用到的相位函数，结合迭代广义解调算法可以将多分量信号中特定时频曲线转换成平行于时间轴的直线这一优点，提出了基于迭代广义解调算法的变转速滚动轴承复合故障特征提取方法。该方法的流程图如图2所示，具体步骤如下：

(1)利用同步测取的目标轴承转频信号获取转频曲线；

(2)根据转频曲线方程以及目标轴承的故障特征系数计算迭代广义解调算法所需的相位函数及相位点；

(3)通过Hilbert变换获取目标轴承的包络信号；

(4)对目标轴承的包络信号进行迭代广义解调得到解调信号；

(5)通过快速傅里叶变换计算解调信号的频率谱；

(6)判断频率谱中突出峰的横坐标值与相位点的关系完成故障诊断。

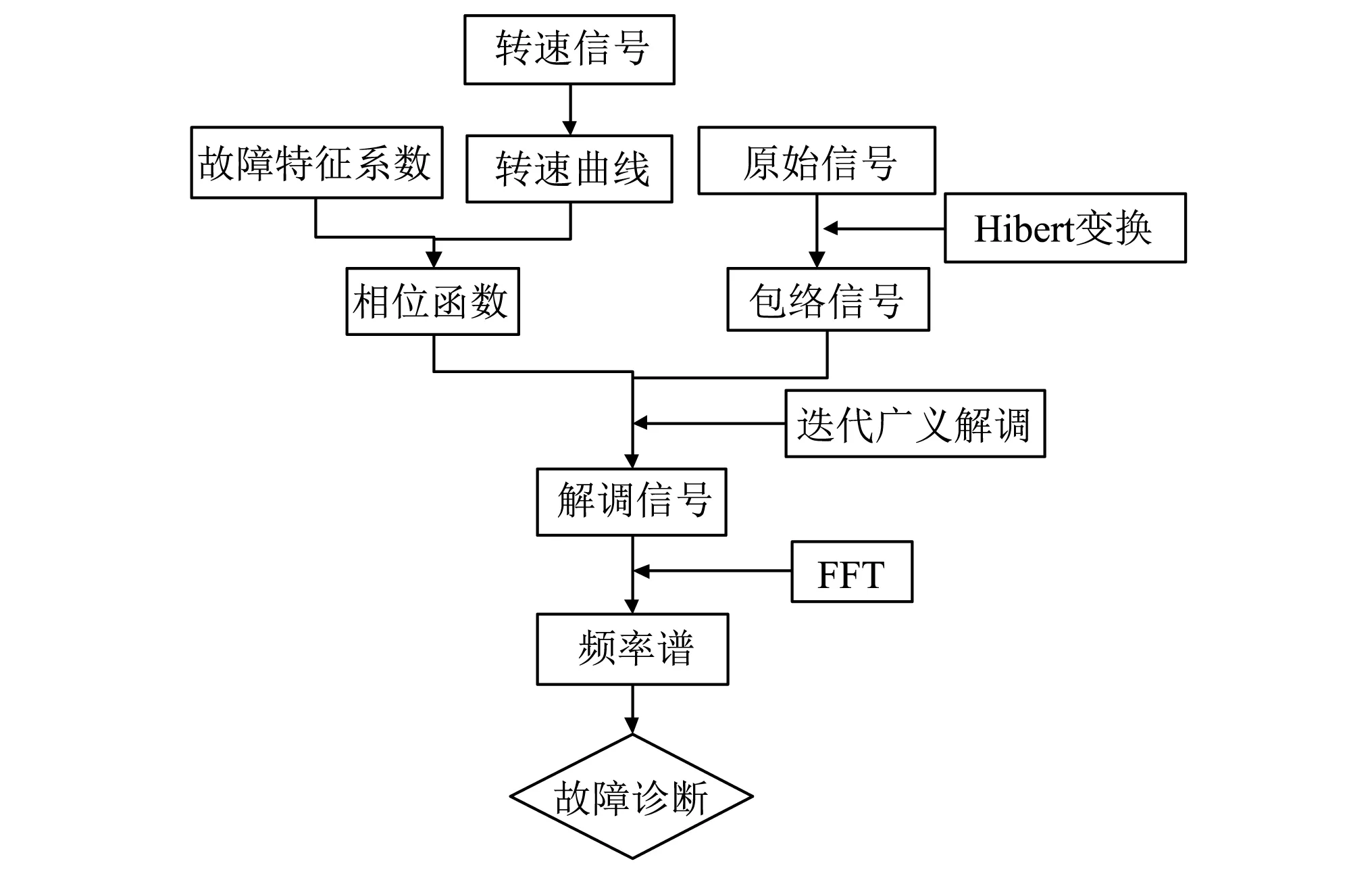
图2 算法流程图Fig.2 Flowchart of the proposed method

2 仿真验证

本节构造了变转速工作模式下滚动轴承复合故障仿真信号对本文算法的有效性进行验证。变转速条件下滚动轴承单一故障仿真信号的构造公式如下：

(5)

式中：N为信号的长度；Am=a·tm+b代表第m个冲击的幅值；β为结构的衰减系数；wr表示轴承故障激起的共振频率；μ(t)为单位阶跃函数；tm表示第m个冲击出现的时间，计算公式如下：

(6)

式中：m=2,3,…,N，f(t)=6t+38表示轴承转频随时间变化的规律；τ代表由滚动体滑移带来的故障冲击间隔之间的误差，其取值一般为0.01～0.02；n代表轴承每转出现的故障冲击数。

根据公式(5)和(6)构造变转速条件下滚动轴承复合故障仿真信号：

xbearing(t)=x1(t)+x2(t)+n(t)

(7)

式中：x1(t)是故障点1引起的冲击脉冲序列，x2(t)是故障点2引起的冲击脉冲序列，n(t)为高斯白噪声。仿真模型的其他参数见表1。

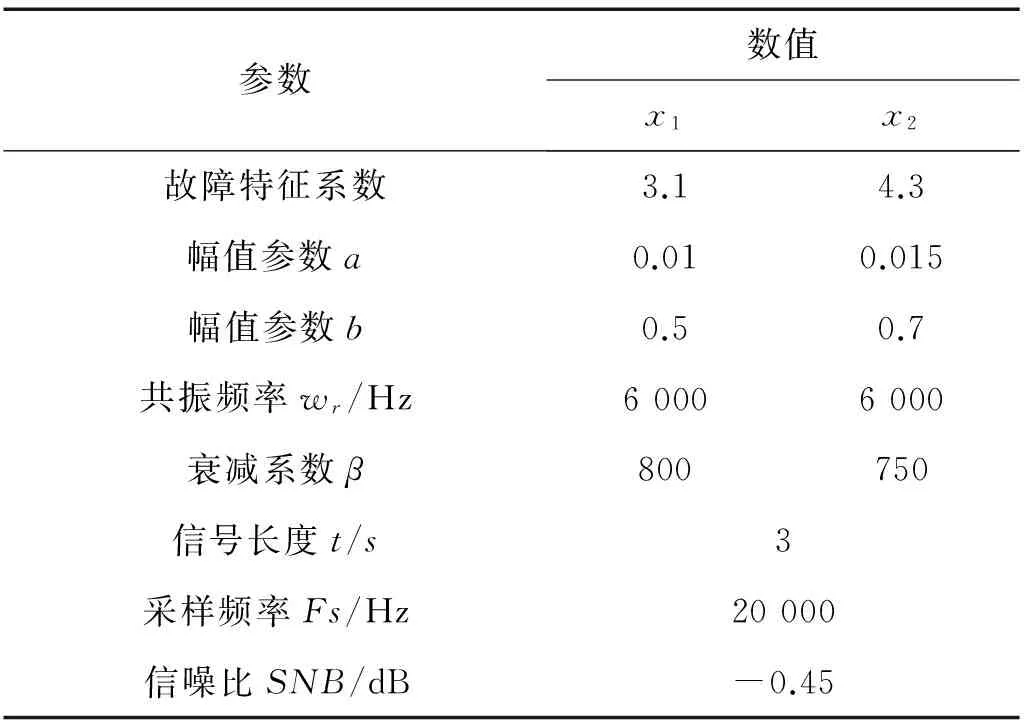
表1 变转速条件下滚动轴承复合故障仿真模型参数

根据上述仿真模型以及参数确定的变转速条件下

滚动轴承复合故障引起的冲击响应(局部)如图3所示。根据图3可以看出，两个故障点产生的冲击相互交叉在一起，有的冲击甚至重叠在一起。仿真信号整体时域波形图如图4所示。

根据仿真信号的频率曲线方程f(t)=6t+38以及故障特征系数确定迭代广义解调算法所需要的相位函数以及相位点如表2所示。为保证及验证故障诊断结果的可靠性，结合故障轴承信号包络时频图中的故障特征频率曲线拥有多条谐波，且各个谐波相对于故障特征频谱分别具有N(N=2,3,…)倍的倍数关系这一特点，本文增加了对故障特征频率趋势线的2倍及3倍谐波的处理。

图3 滚动轴承复合故障冲击脉冲仿真示意图Fig.3 Multi-fault impulses of simulated signal

图4 变转速条件滚动轴承复合故障仿真信号Fig.4 Simulated multi-fault vibration signal

为对比分析，随机选取了一个故障特征系数F3=2.5，以假设该故障轴承还包含第3个故障点。该故障点对应的故障特征频率方程、相位函数以及相位点如表2所示。

表2 故障轴承仿真信号各个故障对应的相位函数及相位点

根据表2中故障点1和2分别对应的3个相位函数以及假设的故障点3对应的相位函数逐次对仿真信号的包络信号进行广义解调，得到解调信号后对解调信号进行FFT，计算的频率谱如图5所示。最后利用表中的各个故障对应的相位点以及频率谱中的突出峰横坐标完成故障诊断。

图5中，以圆圈标注的突出峰横坐标分别为117.5、235和352.5。三组数据分别与故障点1对应的相位点数值相吻合。而图中以箭头标注的3个突出峰对应的横坐标分别为163、326.5和489，分别近似于故障点2所对应的3个相位点。因此可以断定仿真信号中存在两种故障。

另外，图5中在假设的故障点3所对应的相位点95 Hz处不存在明显且独立的突出峰，以此可以说明该仿真信号中不存在所假设的故障点3。

综上分析，本文提出的基于迭代广义解调算法的滚动轴承复合故障诊断方法可以有效的确定目标轴承的故障点的数量和位置。

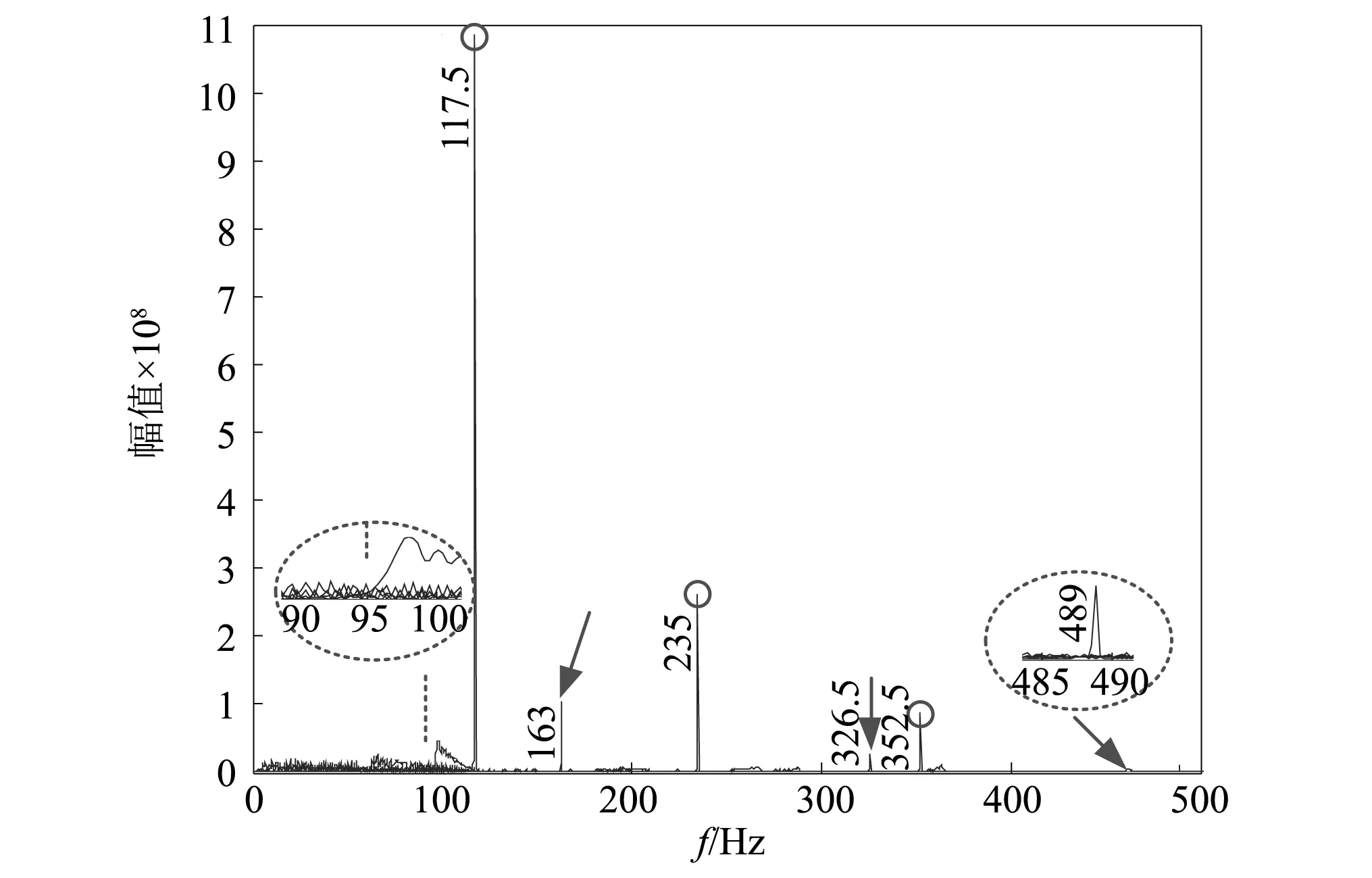
图5 解调信号的频谱图Fig.5 Frequency spectrum of demodulated signal

3 实验验证

本节利用滚动轴承振动试验台上的实测数据对本文算法进行验证。图6为实验装置。其中加速度传感器安装在目标轴承附近以准确测取其振动信号。转速计安装在轴端用于测量轴承转速。采集装置为 YE6231 采集卡及其配套的软件。对滚动轴承进行电火花切割模拟其外圈和内圈裂纹复合故障，其中故障程度分别为轻度故障(宽：0.2 mm,深：0.4 mm)、中度故障(宽：0.4 mm,深：0.6 mm)和重度故障(宽：0.6 mm,深：0.8 mm)。本文选取内圈轻度、外圈中度故障轴承作为实验轴承如图7所示。目标轴承的型号、几何参数以及内外圈和滚动体对应的故障特征系数分别见表3。

图8为测取包含内外圈故障的目标轴承在减速条件下的振动信号，其中采样频率为24 000 Hz，时长为3 s。图9中左下角为同步测取转速脉冲信号(局部)，从中也可以看出随着转速的减小，脉冲逐渐稀疏。根据转速脉冲信号计算得到的转速曲线如图9所示，其拟合方程为f(t)=-0.7t2-5.8t+52.9。

图6 滚动轴承试验台Fig.6 Experimental setup of rolling element bearing

图7 复合故障轴承Fig.7 Target bearing with outer race defect and inner race defect

参数数值轴承型号6000滚动体数n7滚动体直径d/mm4.8节圆直径D/mm17.65接触角α0外圈故障特征系数2.5内圈故障特征系数4.4滚珠故障特征系数1.7

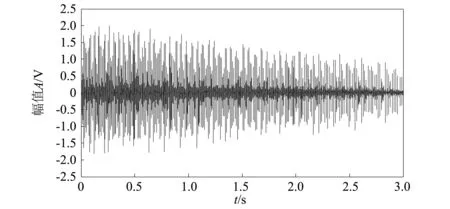
图8 减速条件下复合故障轴承实测信号Fig.8 Measured signal of multi-fault bearing under deceleration

根据转频曲线方程、目标轴承的故障特征系数以及公式(1)～(3)计算得到内、外圈和滚动体对应的故障特征频率趋势线方程。对上述方程分别乘以N(N=2, 3)即可得到内、外圈和滚动体故障特征频率趋势线的二倍及三倍频趋势线方程。上述故障特征频率趋势线方程及其2、3倍频方程以及分别对应的相位函数、相位点分别见表4。

分别根据表4中的9个相位函数对实测信号的包络信号逐次广义解调。解调信号的频率谱如图10所示。图中含有成规律分别且相对独立的突出峰。以圆圈标注的突出峰的横坐标分别为132.2、264.8和396.2。

这与目标轴承外圈故障对应的3个相位点相吻合，即可说明该轴承含有外圈故障。

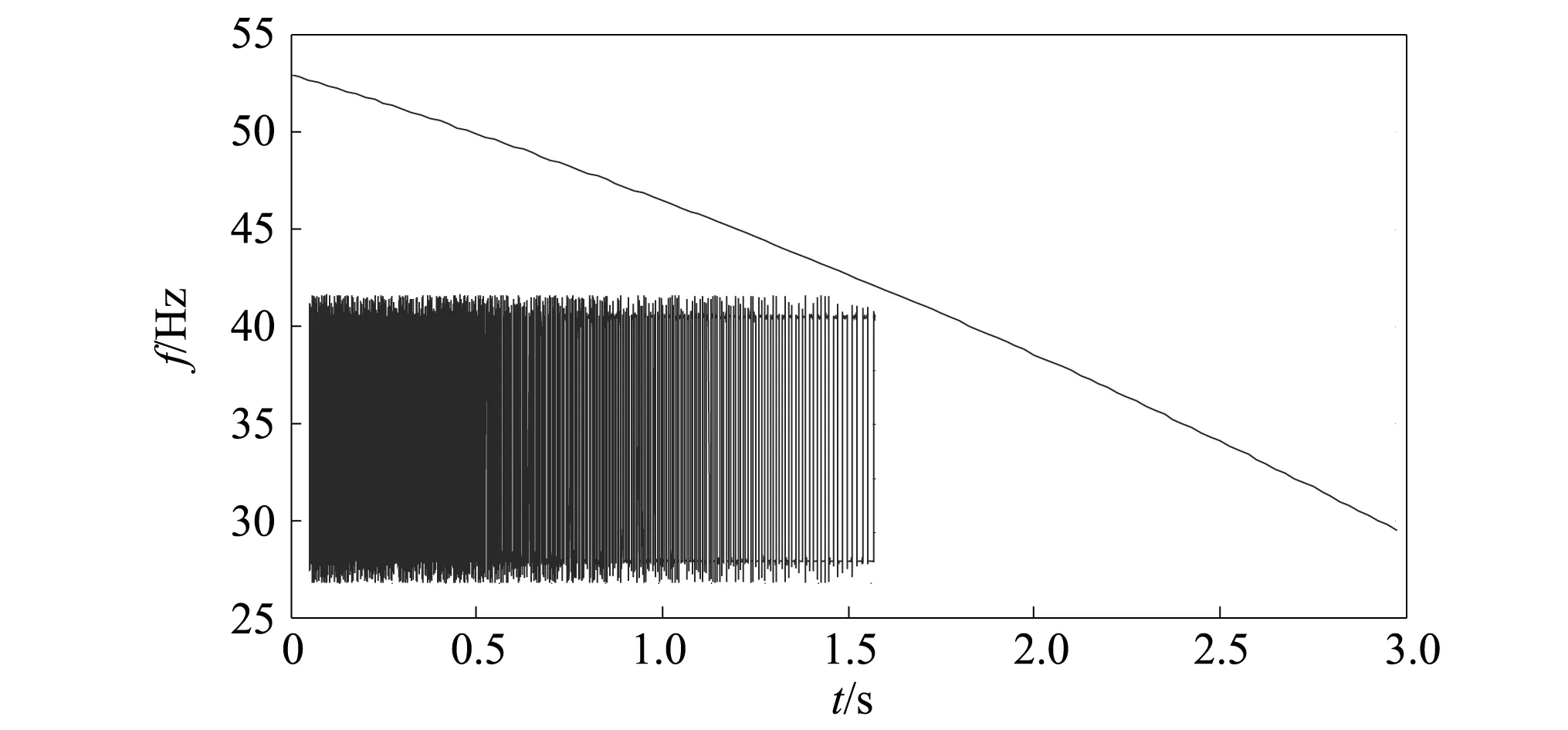
图9 局部转速脉冲信号及转频曲线Fig.9 Rotational frequency curve and partial rotational speed signal

故障位置故障特征系数故障特征频率方程相位函数相位点外圈Fo=2.5fo(t)=-1.75t2-14.5t+132.3so(t)=-0.56t3-7t2fpo=132.32fo(t)=-3.5t2-29t+264.62so(t)=-1.12t3-14t2fpo=264.63fo(t)=-5.52t2-43.5t+396.93so(t)=-1.68t3-21t2fpo=396.9内圈Fi=4.4fi(t)=-3.1t2-25.5t+232.8si(t)=-1.03t3-12.8t2fpi=232.82fi(t)=-6.2t2-51t+465.62si(t)=-2.06t3-25.6t22fpi=465.63fi(t)=-9.3t2-76.5t+698.43si(t)=-3.09t3-38.4t23fpi=698.4滚珠Fb=1.7fb(t)=-1.19t2-9.9t+90sb(t)=-0.4t3-4.95t2fpb=902fb(t)=-2.38t2-19.8t+1802sb(t)=-0.8t3-9.9t22fpb=1803fb(t)=-3.57t2-29.7t+2703sb(t)=-1.2t3-14.85t23fpb=270

图10中以箭头标注的3个突出峰的横坐标分别为234.2、468.2和701.1。后两个突出峰横坐标分别是第一个突出峰横坐标的2倍和3倍的同时，三个突出的横标值与表4中目标轴承内圈故障所对应的3个相位点相吻合。因此可以判断出该目标轴承内圈存在缺陷。

图10 实测信号解调后的频率谱Fig.10 Frequency spectrum of demodulated signal

最后，对目标轴承滚珠的健康状况进行判别。如果滚珠产生表面损伤类故障，图10中横标分别为90、180和270处将会出现明显的突出峰，尤其是在频率为90 Hz处的突出峰最高。然而解调信号频率谱中的上述3个位置并没有出现突出峰(由于一阶故障特征频率的峰值具有较高的幅值优势，因此，图10中只给出了横坐标为90 Hz附近的放大图)。因此可以断定该目标轴承不存在滚珠故障。

为了进一步揭示新方法的优点，本文利用计算阶比分析方法对实测故障轴承信号进行分析作为对比。通过角域重采样和包络分析得到阶比谱如图11所示。图中圆圈标注的峰代表目标轴承外圈故障时对应的阶比，箭头标注的峰代表内圈故障时对应的阶比。通过图10和图11对比得知：其一，包络阶比谱中代表故障阶比的峰聚集性不高，尤其在高阶比处表现更为明显；其二，包络阶比谱中的干扰峰较多，且目标峰幅值优势不明显，易造成误判或漏判。因此本文方法获得的频谱图更简洁，峰值的辨识度更高，也更为有效的提取故障信息，定位故障点位置。

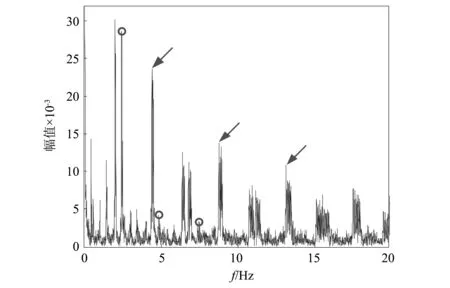
图11 实测信号的包络阶比谱Fig.11 Envelope order spectrum of demodulated signal

4 结 论

本文提出了基于迭代广义解调算法的变转速滚动轴承复合故障特征提取方法。该方法的优势主要表现在以下几个方面：

(1) 利用迭代广义解调算法可以将多分量信号中的多条特定的时频曲线转换成平行于时间轴的直线这一优势消除了转速变化对滚动轴承复合故障特征的影响。

(2)利用滚动轴承复合故障信号的时频特性，即故障信号的包络时频谱中存在明显的且与转频成固定规律变化能明确表征轴承故障类型的时频曲线，转频曲线以及故障特征系数确定相位点用以判断轴承的故障数量及位置。

(3)该算法无需角域重采样即可完成复合故障特征的提取。另外，信号的处理过程只针对信号中表征轴承故障的特定成分，免除了其他成分的干扰，为变转速条件下滚动轴承复合故障特征的提取提供了新思路。

需要指出的是本文方法仅适用于目标轴承某一部件上只包含一处故障点的复合故障情况，例如内圈、外圈和滚珠上都存在一处故障点。

[ 2 ] 王晓冬,何正嘉, 訾艳阳.小波自适应构造方法及滚动轴承复合故障诊断研究[J]. 振动工程学报, 2010, 23(4): 438-444.

WANG Xiaodong, HE Zhengjia, ZI Yanyang. Adaptive construction of multiwavelet and research on composite fault diagnosis of rolling bearing[J]. Journal of Vibration Engineering, 2010, 23(4): 438-444.

[ 3 ] LUO Jiesi, YU Dejie, LIANG Ming. Application of multi-scale chirplet path pursuit and fractional Fourier transform for gear fault detection in speed up and speed down processes [J]. Journal of Sound and Vibration, 2012, 331:4971-4986.

[ 4 ] 赵德尊, 李建勇, 程卫东. 变转速及齿轮噪源干扰下基于IDMM与EMD的滚动轴承故障诊断方法[J]. 振动与冲击, 2016, 35(10): 101-119.

ZHAO Dezun, LI Jianyong, CHENG Weidong. Method for rolling element bearing fault diagnosis based on IDMM and EMD under time-varying rotational speed and gear noise [J]. Journal of Vibration and Shock, 2016, 35(10): 101-119.

[ 5 ] 明安波,褚福磊,张炜. 滚动轴承复合故障特征分离的小波-频谱自相关方法[J]. 机械工程学报，2013,49(3): 80-87.

MING Anbo, CHU Fulei, ZHANG Wei. Compound fault features separation of rolling element bearing based on the wavelet decomposition and spectrum auto-correlation [J]. Journal of Mechanical Engineering, 2013, 49(3): 80-87.

[ 6 ] 马新娜, 杨绍普. 滚动轴承复合故障诊断的自适应方法研究[J]. 振动与冲击, 2016, 35(10):145-150.

MA Xinna, YANG Shaopu. Adaptive compound fault diagnosis of rolling bearings [J]. Journal of Vibration and Shock, 2016, 35(10): 145-150.

[ 7 ] CHEN Jinglong, ZI Yanyang, HE Zhengjia, et al. Compound faults detection of rotating machinery using improved adaptive redundant lifting multiwavelet [J]. Mechanical Systems and Signal Processing, 2013, 38: 36-54.

[ 8 ] ZHANG Haibin, LU Siliang, HE Qingbo, et al. Multi-bearing defect detection with trackside acoustic signal based on a pseudo time-frequency analysis and Dopplerlet filter [J]. Mechanical Systems and Signal Processing, 2016, 70/71: 176-200.

[ 9 ] FYFE K R, MUNCK E D S. Analysis of computed order tracking [J]. Mechanical System and Signal Processing, 1997, 11(2): 187-205.

[10] RANDALL R B, ANTONI J. Rolling element bearing diagnostics-a tutorial [J]. Mechanical Systems and Signal Processing, 2011, 25 (2): 485-520.

[11] SAAVEDRA P N, RODRIGUEZ C G. Accurate assessment of computed order tracking [J]. Shock and Vibration, 2006, 13 (1): 13-21.

[12] CHENG Weidong, ROBERT X G, WANG Jingjiang, et al. Envelope deformation in computed order tracking and error in order analysis [J]. Mechanical System and Signal Processing, 2014, 48(1/2): 92-102.

[13] OLHEHE S, WALDEN A T. A generalized demodulation approach to time-frequency projections for multicomponent signals [J]. Proceedings of the Royal Society A, 2005, 461(2059): 2159-2179.

[14] CHENG Junsheng, YANG Yu, YU Dejie. Application of the improved generalized demodulation time-frequency analysis method to multi-component signal decomposition [J]. Signal Processing, 2009, 89: 1205-1215.

[15] 黄椒治, 林慧斌, 丁康. 基于广义解调平滑能量分离算法的瞬时频率估计[J]. 振动工程学报, 2014, 27(2): 281-288.

HUANG Jiaozhi, LIN Huibin, DING Kang, Instantaneous frequency estimation based on generalized demodulation smoothed energy separation algorithm [J]. Journal of Vibration Engineering, 2014, 27(2): 281-288.

[16] 皮维, 于德介, 彭富强. 基于多尺度线调频基稀疏信号分解的广义解调方法及其在齿轮故障诊断中的应用[J]. 机械工程学报, 2010, 46(15): 59-64.

PI Wei, YU Dejie, PENG Fuqiang. Generalized demodulation method based on multi-scale chirplet and sparse signal decomposition and its application to gear fault diagnosis [J]. Journal of Mechanical Engineering, 2010, 46(15): 59-64.

[17] FENG Zhipeng, CHU Fulei, ZUO Mingliang. Time-frequency analysis of time-varying modulated signals based on improved energy separation by iterative generalized demodulation [J]. Journal of Sound and Vibration, 2011, 330: 1225-1243.

[18] CHEN Xiaowang, FENG Zhipeng. Iterative generalized time-frequency reassignment for planetary gearbox fault diagnosis under nonstationary conditions [J]. Mechanical Systems and Signal Processing, 2016, 80: 429-444.