含功能梯度材料的周期管路振动特性研究

杜春阳, 郁殿龙, 温激鸿, 刘江伟, 贾鹏飞

(国防科学技术大学 装备综合保障技术重点实验室,长沙 410073)

管路系统通常用来传递能量或物质，广泛应用与船舶动力、航空航天等领域。充液管路系统是管路系统中最常见的一种结构形式。充液管路系统中存在液体的压力波脉动、管壁振动以及两种振动的相互耦合。当振动的频率与管路系统的固有频率相重合时，会发生共振现象，危害较大[1]。现阶段的管路减振措施主要有设置支撑、安装阻振质量、安装挠性接管[2]、安装动力吸振器，贴敷阻尼材料等[3]。这些措施虽然可以一定程度的解决管路的振动问题，但也存在一定缺陷。

基于声子晶体理论，设计周期性管路系统，可以有效的对某些特定频段的振动进行控制与削弱[4]，但是由于周期性管路由两种或多种材料周期性组成，在两种不同材料的结合处由于两边的材料性能不同，产生应力集中问题比较突出。

为解决上述问题，在本篇论文中，在基于声子晶体理论设计的经典周期管路系统的基础上，周期性的嵌入功能梯度材料(Functionally Graded Materials，FGM)，分析功能梯度材料对带隙和应力集中的影响。

功能梯度材料由于其特殊的性能如高刚度，减小残余应力和热应力等受到许多研究学者的关注[5-6]。选用两种或多种性能不同的材料，通过连续的改变这两种或多种材料的组成和结构，使其界面消失导致材料的性能随着材料的组成和结构的变换而缓慢变化，形成功能梯度材料[7]。吴晓等[8]采用Timoshenko梁修正理论研究了功能梯度材料梁的动力响应问题，证明了不同梯度指数能对梁的固有振动频率和动力响应产生影响。Yang等[9]分析了含功能梯度材料的带孔板的应力集中问题。沈惠杰等[10]利用有限元法研究了含功能梯度材料的圆柱壳体的带隙特性。Wu等[11]利用有限元法和传递矩阵法计算了应用功能梯度材料的一维声子晶体的能带结构，并对其影响影响因素进行了分析。Chakraborty等[12]应用谱有限元法对功能梯度材料梁在高频载荷下的波传播行为进行了研究。不同于功能梯度材料径向分布的梁， Shahba等[13-14]分析计算了功能梯度材料轴向分布梁的振动特性。上述分析主要集中在FGM对周期管路的带隙调节，对消除应力集中研究尚不深入。本文将在现有研究的基础上，研究含功能梯度材料周期管路的带隙特性，并分析了其对于管路应力集中的削弱作用。

1 模型计算

相较于经典周期管路，含功能梯度材料的周期管路在结构上的显著差别就是在两种材料之间采用一段沿轴向材料参数均匀变化的功能梯度材料构成的管路来进行衔接。

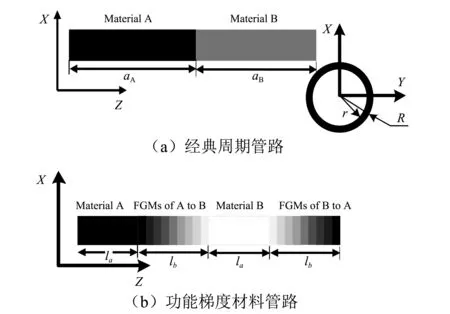
图1 管路理论模型Fig.1 The sketch of periodic pipe with FGMs and classic periodic pipe

梁模型和壳模型是研究充液管路振动主要采用的两种理论模型。充液管路振动模式有轴向振动、扭转振动、弯曲振动，以及它们之间的复杂耦合振动。其中弯曲振动在振动模式中占主要分量。因此，研究弯曲振动对管路振动控制具有重要的理论意义。研究管路弯曲振动大多数基于梁模型理论[15]。一般情况下，充液管路长度与管外径之比较大，振动时更多地表现出梁模态特性，周向模态可忽略。本文研究的管路符合这些特点，因此重点介绍两种梁模型—Timoshenko梁模型和Euler梁模型,由于其振动方程包含了截面转动惯量和剪切变形项，使得Timoshenko梁模型比Euler梁模型更精确，本文采用Timoshenko梁模型，利用有限元法，划分细小单元，对细小单元进行处理。有限元法对固体材料以黏合形式接触的结构与运动分析特别有效，此外，采用有限元法，可将流体与弹性管壁作为耦合系统考虑，分析流固耦合作用下充液管路的振动[16]。

(1)

进一步，通过求解矩阵T的特征值，即可得到Bloch波矢与频率的关系。

(2)

COMSOL Multiphysics是一款高度集成的大型工程模拟软件，提供几何结构创建、网格剖分、物理过程定义、计算求解、数据可视化及后处理等功能，可通过附加激励信号来计算分析模型的特性[17]。COMSOL软件已经被广泛应用于周期结构和声学超材料的研究中[18-21]，应用COMSOL软件，可以通过设置周期边界条件，有效计算能带结构和传播特性。

2 带隙特性计算：

在计算中，管路沿z方向周期排列，功能梯度材料的材料性能采用函数过渡，单元管路中材料参数过渡函数如式(3)所示[9]

(3)

式中：ψA-B和ψB-A分别为图1(b)管路单元中两段功能梯度材料接管的材料属性，ψA和ψB是材料A和材料B的材料属性(密度和杨氏模量等)，la、lb分别为单材料管路长度和功能梯度材料管路长度，z是管路上的点的Z坐标值。如图1(b)所示的功能梯度材料管路单元，当式(3)中的n取值为1时，材料参数按照一个一次函数进行变化，随着管路上点的z坐标变化，管路的材料参数从一种材料过渡到另一种材料。当n取值变化时，过渡函数将呈现出如图2所示的不同函数特性。

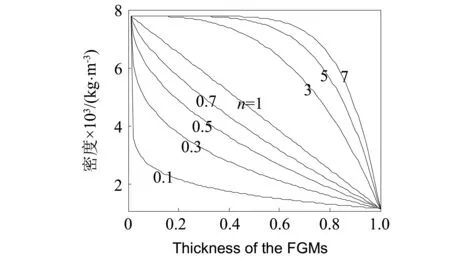
图2 功能梯度材料密度在不同n值下沿轴向变化示意图Fig.2 Variation of density along the beam axis with different exponent n

3.1 功能梯度材料周期管路带隙特性

计算中，材料A采用钢，材料B采用环氧树脂，两者的性能参数，见表1。

表1 材料结构参数

表2 功能梯度材料管路结构参数

根据表2的结构参数进行建模与仿真，采用n=1的情况，材料性质以一次函数过渡。利用COMSOL软件计算能带结构，如图3所示，图3色散曲线从波矢0处出现三条色散曲线，分别对应纵向、扭转和弯曲振动波。在计算其频响曲线时，选用五个管路单元，在管路的管壁上分别施加相应的单位激励(弯曲，扭转，轴向)，在另一端的管壁上进行信号拾取，利用拾取的信号获得相应振动的频响曲线。根据带隙曲线得知，能带结构图中包含了多种类型振动的带隙，结合振动频响曲线与能带结构图综合分析得知，图中2 000 Hz以下有三个弯曲振动带隙，分别为97.48 ～141 Hz，429.7～900.1 Hz，1226～1 490 Hz；有两个扭转振动带隙分别为343～900.9 Hz，1 231～1 696 Hz；有两个轴向振动带隙565～907 Hz，1 231～1 490 Hz。

通过分析能带结构和频率响应曲线，可以发现在563.1 ～900.1 Hz，1 226 ～1490 Hz频率范围内三种振动带隙都共存，可以有效抑制各种振动模式的传播。

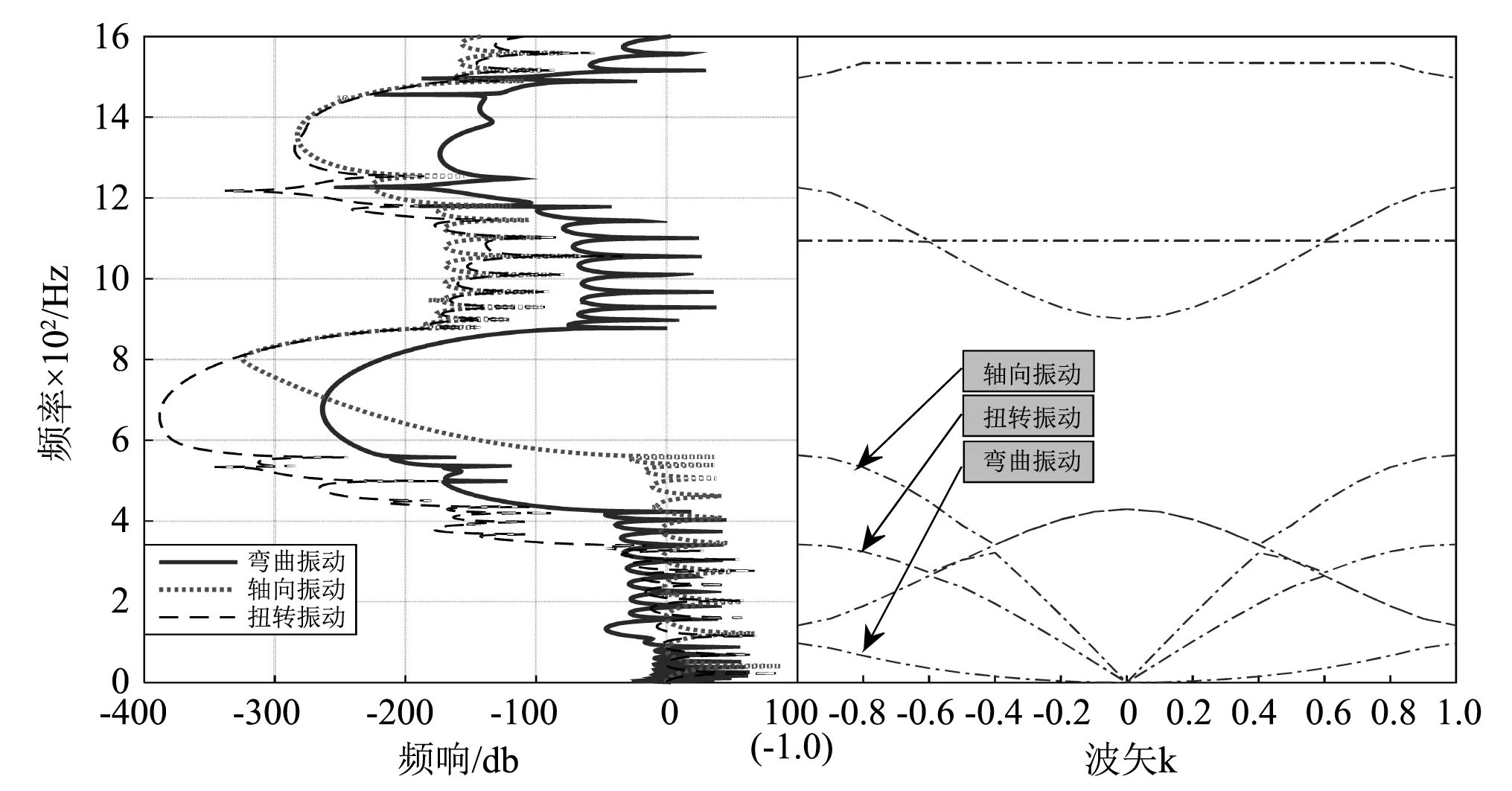
图3 功能梯度材料以一次函数过渡Fig.3 The vibration band structures and FRF of periodic pipe with FGMs for n=1

鉴于弯曲振动控制在管路减振中的重要意义，我们主要考虑弯曲振动的带隙位置以及宽度的变化。为了进一步验证功能梯度材料管路的带隙特性，将其与经典周期管路进行比较。

表3 经典周期管路结构参数

利用COMSOL计算出经典周期管路的能带曲线，对比两者弯曲振动带隙的变化。

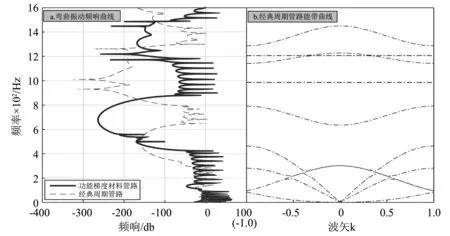
图4 经典周期管路与功能梯度材料管路带隙图与频响曲线比较Fig.4 The comparison of vibration band structures and the flexural vibration FRF between periodic pipe with FGMs and classic periodic pipe

分析比较其带隙特性，经典周期管路三个带隙分别为84.32～95.18 Hz，302.4～634 Hz，792.4～1 286 Hz在带隙范围内，管壁的弯曲振动均不能传播。相较于经典管路，含功能梯度材料的管路第一带隙的位置虽然没产生太大的变化，但是带隙的宽度拓宽了，带隙内振动衰减也明显得到增强。由于经典周期管路的第一带隙频率范围只有10 Hz左右，所以其频响曲线中第一带隙的衰减特性很弱，但是从含功能梯度材料的周期管路的频响曲线可以很明显的看出第一带隙位置和其衰减特性。第二带隙中心频率向高频偏移，但是宽度却增加了。

2.2 带隙影响因素

2.2.1 过渡函数对带隙特性的影响

功能梯度材料管路的结构参数不变，采用表2的相应结构参数，改变过渡函数的指数值，使得n的值为0.1、1、10。分别计算其弯曲振动的频响曲线，分析不同过渡函数对于管路带隙特性的影响。

图5(a)中，三种n值的管路第二带隙对弯曲振动的衰减程度有相应的差异，n=10时衰减程度最强，并且带隙的中心最低，n=0.1衰减程度最弱，n=1带隙中心最高且带隙最宽。第三带隙对振动衰减的区别更为明显，与第二带隙的规律相似，n=10时衰减程度最大带隙中心最低，但是n=1时振动衰减效果最差，带隙中心最高且带隙最窄。

图5(b)中，放大了0～200 Hz位置的频响曲线，n=1时衰减程度最强，带隙宽度也最宽，而其他两组的带隙都比较窄，衰减也较弱。

2.2.2 功能梯度材料管路长度对带隙特性的影响

晶格常数不变，改变的值，改变功能梯度材料管路在单元管路中的配比，过渡函数选用一次函数(n=1)，lb的值分别为0.25 m，0.2 m，0.1 m，分别计算其弯曲振动的频响曲线。

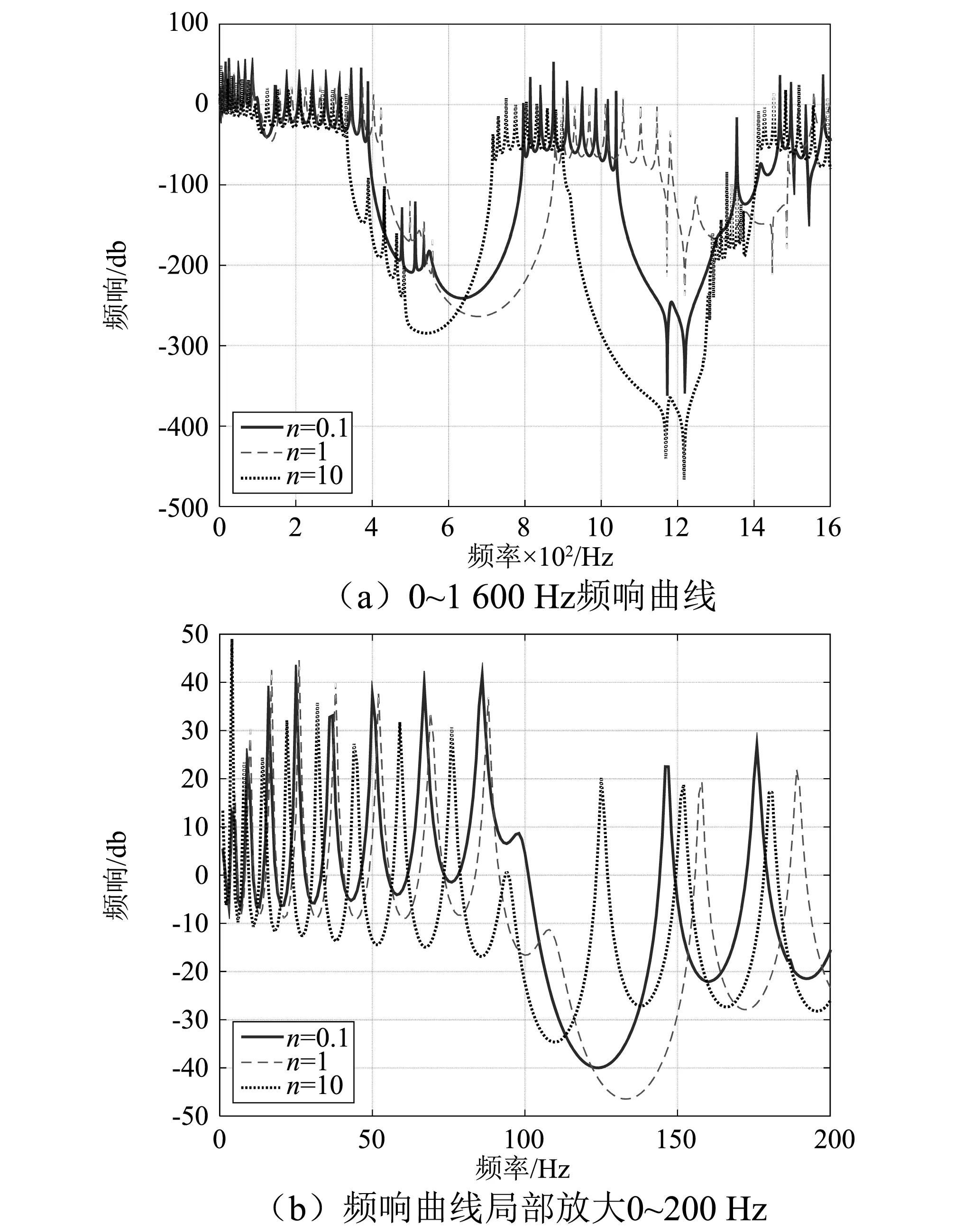
图5 不同过渡函数指数n频响曲线比较Fig.5 The flexural vibration FRF of periodic pipe with FGMs for different exponent n

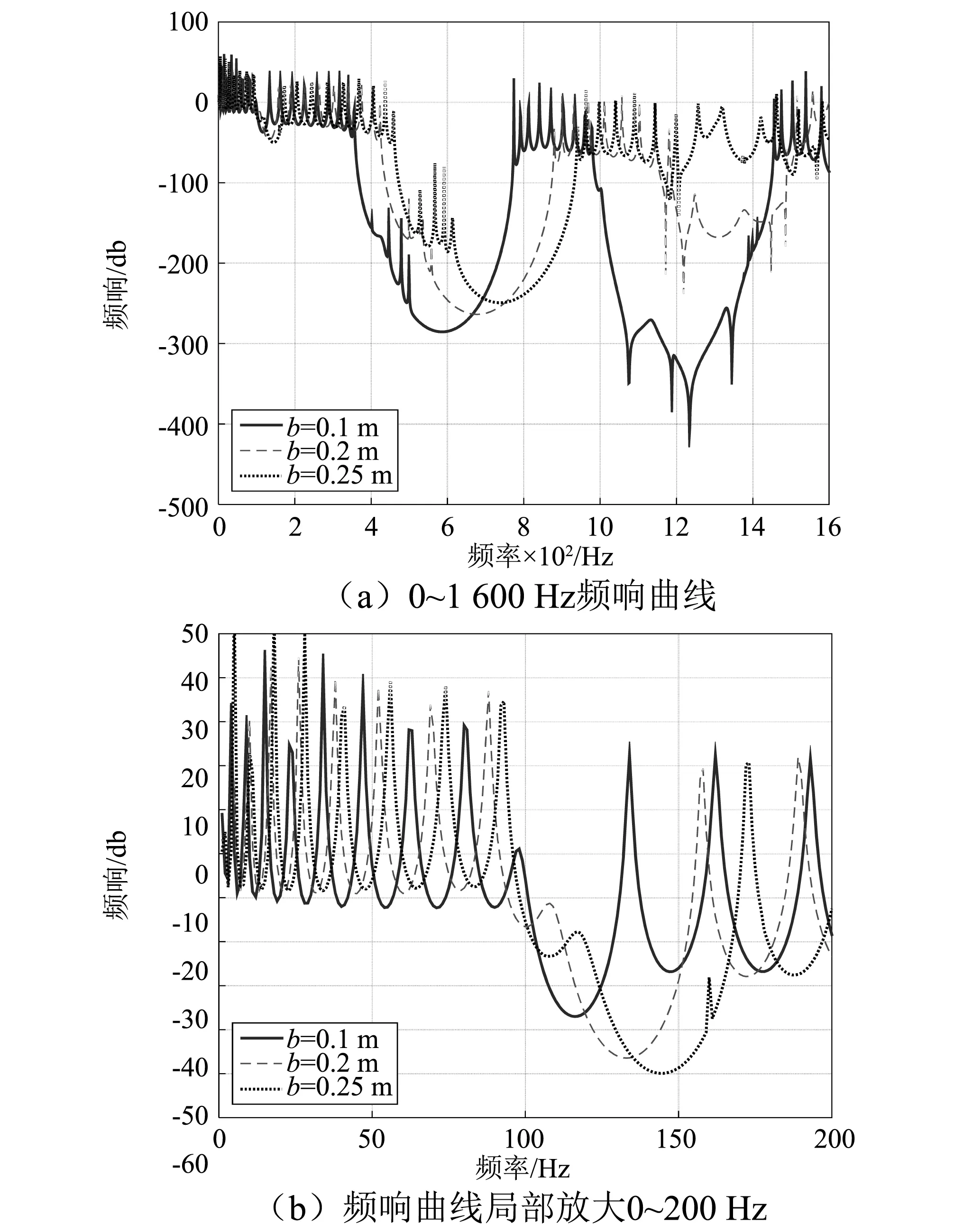
图6 不同功能梯度材料管路长度频响曲线比较Fig.6 The flexural vibration FRF of periodic pipe with different length FGMs

图6(a)中，随着lb值的增加，单元管路内功能梯度材料管路的配比增加，二、三带隙的带隙中心向高频偏移，对于振动的衰减能力削弱。

图6(b)中，放大了0～200 Hz位置的频响曲线，随着lb值的增加，第一带隙中心向高频偏移，带隙变宽，并且对于振动的衰减作用变强。

通过上述仿真，可以得出结论：功能梯度材料对于管路的带隙有一定的影响，通过改变不同的功能梯度材料在单元管路中所占的比例，以及不同的指数函数，可以综合的分析功能梯度材料对周期管路的带隙特性的影响。仿真中选用三种功能梯度材料管路长度配比，分别取值为：lb=0.25 m，lb=0.2 m，lb=0.1 m。指数n值分别取0.1、0.3、0.5、0.7、0、3、5、7。考虑前两个带隙的位置，分析管路的弯曲振动带隙的位置和宽度变化(见图7)。

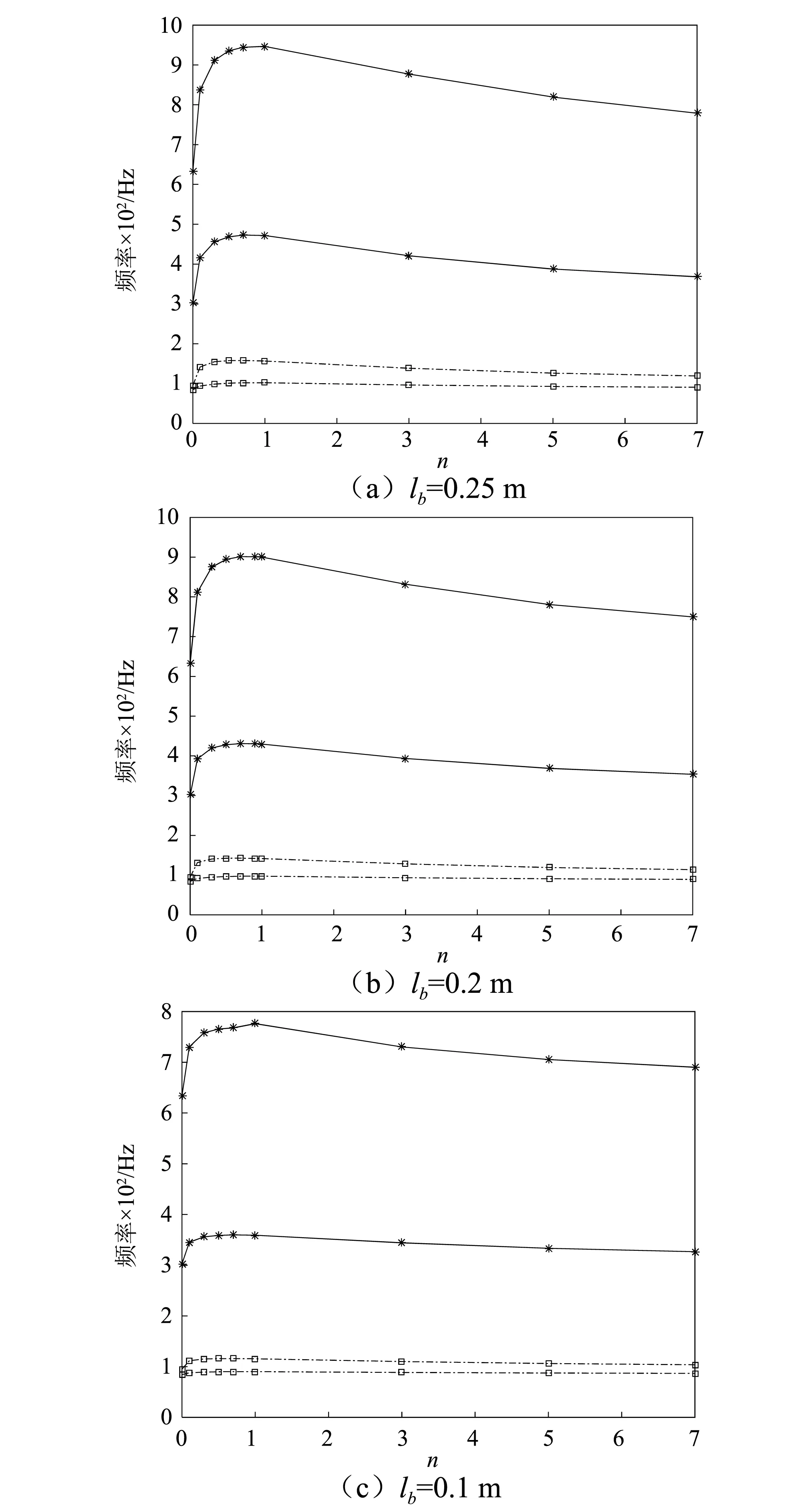
图7 不同长度配比下带隙的变化Fig.7 The flexural vibration band gaps of periodic pipe with different length FGMs and different exponent n

图7是带隙的位置分布图，两类标记不同的曲线分别代表第一带隙和第二带隙的位置。从带隙的分布图中可以看出不同的占比的功能梯度材料管路在指数n变化时，所表现出的规律基本一致，n=0时，管路为经典管路，第一带隙较窄，宽度约为10 Hz，第二带隙起始点为300 Hz，截止约600 Hz，宽约300 Hz。n值从0升至7时，第一带隙和第二带隙的起始首先向高频偏移，到了n≥1时，起始频率开始向低频偏移；第一带隙和第二带隙的宽度也随着n值的变化发生相应的变化，n≤1时，带隙的宽度与n值的大小成正相关，n≥1时，带隙的宽度与n值的大小成负相关。对于不同的lb值，也就是不同的功能梯度材料管路长度，当lb值减小时，第一带隙和第二带隙的起始频率向低频移动，但是带隙的宽度也同样出现了减小。第一带隙的起始频率随着n值和lb值的影响相较于第二带隙来说比较小，但是其带隙宽度影响却较为明显，对比与经典周期管路的10 Hz，lb=0.25 m，n=1时，第一带隙的带隙宽度可以达到57 Hz左右。

3 功能梯度材料对应力集中的影响

功能梯度材料对管路的应力集中问题有一定的减缓作用。计算中，建立五个周期单元的管路模型，在管路的一段加一个垂直于管路轴线的力，在COMSOL中进行扫频，频率范围为1～1 600 Hz，选取几个频率点进行观测，分析弯曲振动的应力分布情况。

首先建立一个经典周期管路模型，参数与表1,3一致。选取的观测频率点290 Hz属于通带位置，90 Hz，500 Hz属于带隙位置，应力分布情况如图8所示。

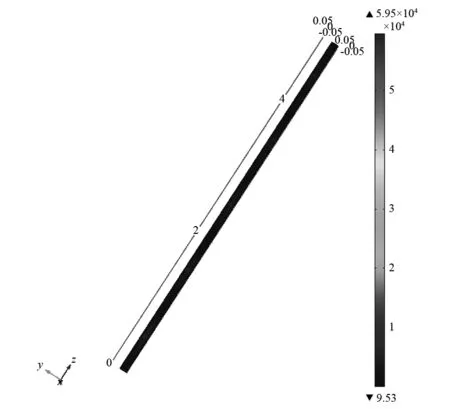
(a) 频率90 Hz

(b) 频率500 Hz

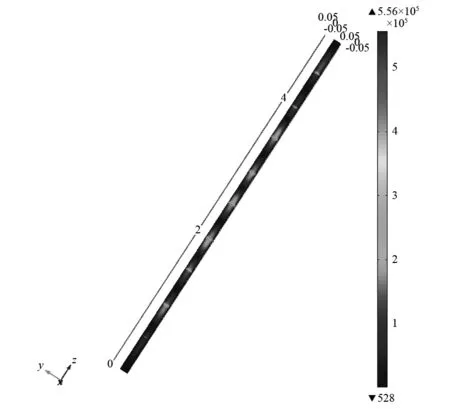
(c) 频率290 Hz

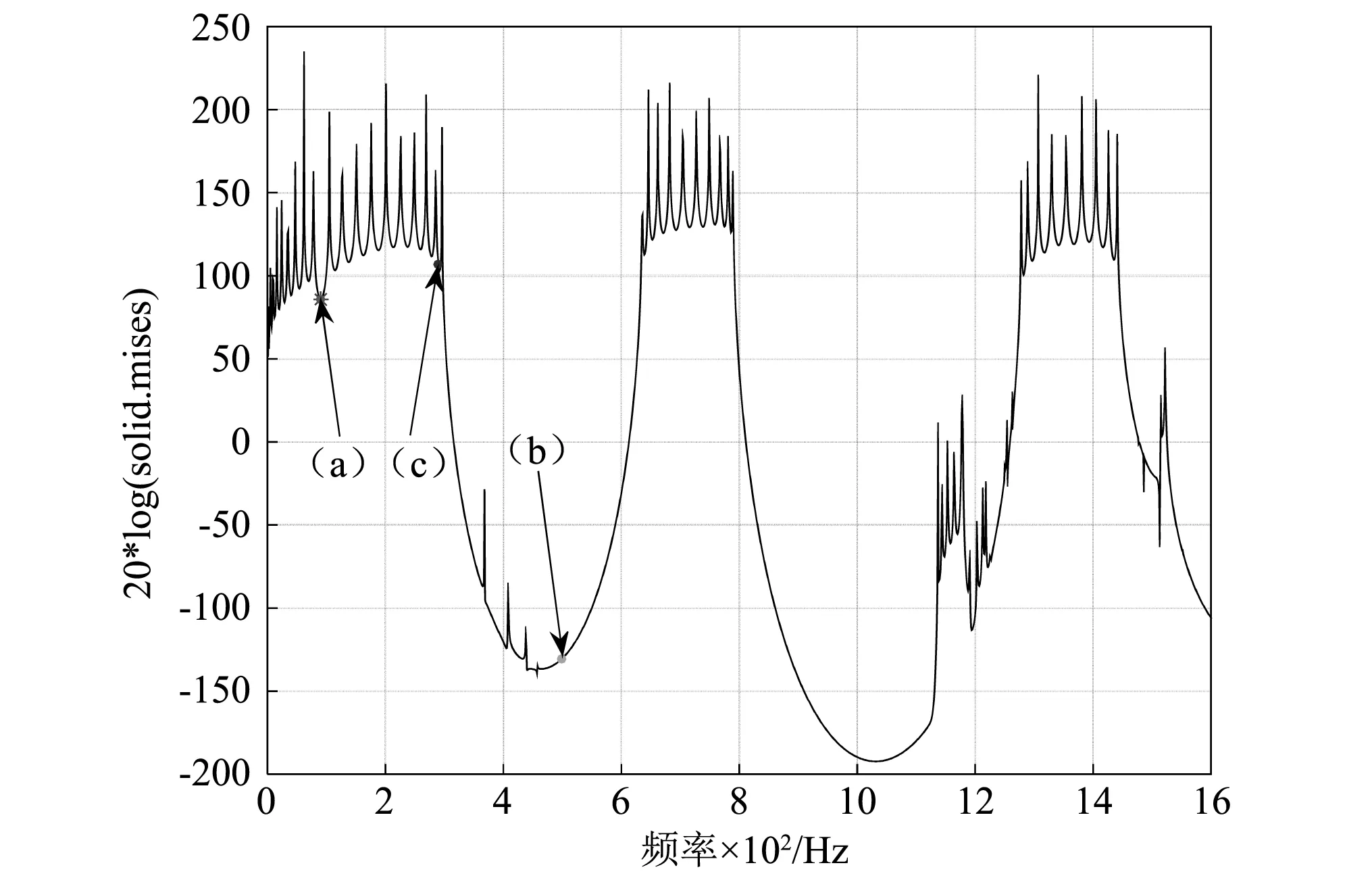
图9 有限周期管路应力传输特性Fig.9 The stress FRF of finitely classic periodic pipe

图9是有限周期管路另一端管壁的应力随频率的变化曲线，三个观测点分别在图中对应指出。从图8,9看出，在带隙范围内，应力主要集中在靠近激励端的前一个或者两个单元内，而后面几个单元应力集中问题比较小，带隙频率范围内的管路应力集中问题可以有效抑制。但当激励频率处于通带位置时，应力在管路系统的所用单元上都有分布，应力集中的问题很明显，在实际应用中，可以通过对管路系统进行设计，可以通过设计带隙位置衰减特定频率的振动传播以及管路系统的应力集中问题。

当加入功能梯度材料后，管路的带隙特性发生了较大的变化，建立一个lb=0.2 m，n=1的模型，其他参数与表1,2一致。同样观测这几个频率点的管路的应力分布。但是由于带隙特性发生变化，90 Hz，290 Hz为通带位置，500 Hz仍处于带隙位置，应力分布情况如图10所示。

经典周期管路的结论在功能梯度材料管路上一样适用，在带隙范围内，应力主要集中于前一个或者两个单元，后面的单元基本上不受到影响。但是在通带范围内的两个观测点的应力分布出现了不同于经典管路的情况，90 Hz和290 Hz位置的应力只集中于前两个单元。由于功能梯度材料管路与经典周期管路的带隙特性相差较大，根据图4的频响曲线，选择0～300 Hz进行应力的比较分析，在此频段内，两种管路的能带结构基本都处于通带范围内。

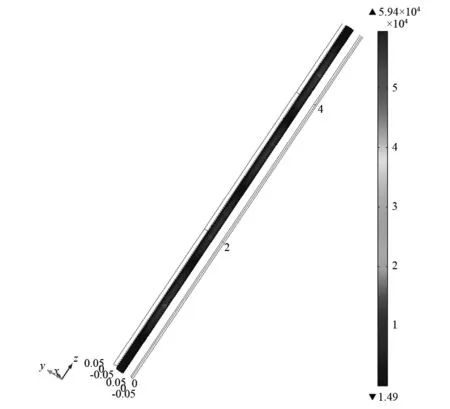
(a) 频率90 Hz

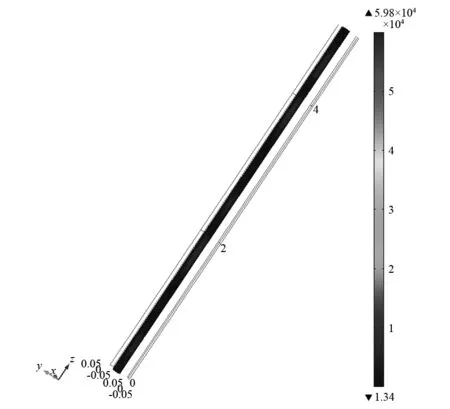
(b) 频率290 Hz

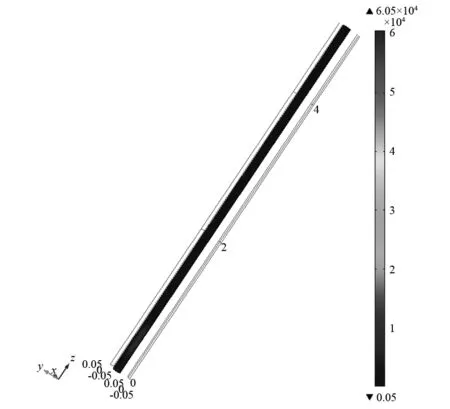
(c) 频率500 Hz

两类管路的应力随频率变化都基本满足带隙规律，在带隙范围内，观测的应力值很小，故应力没有向后方单元传播。同样在通带范围内，含功能梯度材料的管路的应力值明显小于经典周期管路。表明功能梯度材料可以有效的消除周期管路单元的应力集中问题。

4 结 论

利用有限元法，基于声子晶体理论，考虑了功能梯度材料在周期直管管路系统中的应用，研究了功能梯度材料周期管路的带隙特性以及对管路的应力集中影响。

与经典周期管路相比，包含功能梯度材料的周期管路明显改变了带隙的位置与带隙的宽度。改变函数的指数值，改变功能梯度材料在管路单元中所占的比例，可以获得不同的带隙效果。

(1)相较于经典周期管路，功能梯度材料可有效调节周期管路的带隙特性，使得第一带隙出现了明显的拓宽。而其他两个带隙都会产生相应的中心位置的偏移和带隙宽度的变化。

(2)功能梯度材料能够很好的消除周期管路不同材料界面处产生的应力集中问题，可以有效的减缓管路系统的应力损伤。

[ 1 ] SHEN Huijie, WEN Jihong, YU Dianlong, et al. Stability of fluid-conveying periodic shells on an elastic foundation with external loads[J]. Journal of Fluids and Structures, 2014, 46: 134-148.

[ 2 ] 陈刚，朱石坚．管壁不连续对管路结构振动传递的影响[J]．海军工程大学学报，2004，16(2)： 40-43

CHEN GANG, ZHU Shijian. Effects of discontinuity of pipe wall on transmission coefficient of pure torsion wave[J]. Journal of Naval University of Engineering，2004，16(2)： 40-43

[ 3 ] 方丹群, 张斌, 孙家麒, 等. 噪声控制(上册)[M]. 北京: 科学出版社, 2013,4: 848-863

[ 4 ] 沈惠杰, 温激鸿, 郁殿龙,等.基于Timoshenko梁模型的周期充液管路弯曲振动带隙特性和传输特性[J].物理学报, 2009, 12(8): 257-263.

SHEN Huijie, WEN Jinhong, YU Dianlong, et al. Flexural vibration property of periodic pipe system conveying fluid based on Timoshenko beam equation [J]. Acta Physics Sinica, 2009, 12(8): 257-263.

[ 5 ] SHAHBA A, ATTARNEJAD R, TAVANAIE MARVI M, et al. Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions[J]. Composites Part B Engineering, 2011, 42(4): 801-808.

[ 6 ] BEREZOVSKI A, ENGELBRECHT J, MAUGIN G A. Numerical simulation of two-dimensional wave propagation in functionally graded materials[J]. European Journal of Mechanics A/Solids, 2003, 22(2): 257-265.

[ 7 ] BRUCK H A. A one-dimensional model for designing functionally graded materials to manage stress waves[J]. International Journal of Solids & Structures, 2000, 37(44): 6383-6395.

[ 8 ] 吴晓，罗佑新.用Timoshenko梁修正理论研究功能梯度材料梁的动力响应[J].振动与冲击, 2011, 30(10): 245-248.

WU Xiao, LUO Youxin. Dynamic responses of beam with functionally graded materials with Timoshenko beam correction theory[J]. Journal of Vibration and Shock, 2011, 30(10): 245-248.

[ 9 ] YANG Quanquan, GAO Cunfa, CHEN Wentao. Stress concentration in a finite functionally graded material plate[J]. Science China Physics Mechanics & Astronomy, 2012, 55(7): 1263-1271.

[10] SHEN H J, WEN J H, PAÏDOUSSIS M P, et al. Control of sound and vibration for cylindrical shells by utilizing a periodic structure of functionally graded material[J]. Physics Letters A, 2012, 376(45): 3351-3358.

[11] WU Meling, WU Liangyu, YANG Wenpei，et al. Elastic wave band gaps of one-dimensional phononic crystals with functionally graded materials[J]. Smart Materials & Structures, 2009, 18(11): 269-273.

[12] CHAKRABORTY A, GOPALAKRISHNAN S. A spectrally formulated finite element for wave propagation analysis in functionally graded beams[J]. International Journal of Solids and Structures, 2003, 40(10): 2421-2448.

[13] SHAHBA A, RAJASEKARAN S. Free vibration and stability of taperes Euler-Bernouli beams made of axially functionally graded materials[J]. Applied Mathematical Modelling, 2012, 36(7): 3094-3111.

[14] KUKLA S, RYCHLEWSKA J. Free vibration analysis of functionally graded beams[J]. Journal of Applied Mathematics & Computational Mechanics, 2013, 12(2): 39-44.

[15] 沈惠杰. 基于带隙理论的管路系统振动特性研究[D]. 长沙：国防科学技术大学，2009.

[16] 张亚峰. 声子晶体管路减振降噪研究[D]. 长沙：国防科学技术大学，2014.

[17] 中仿科技公司. COMSOL Multiphysics有限元法多物理场建模与分析[M]. 北京：人民交通出版社，2007.

[18] ZHANG Hao, WEN Jihong, XIAO Yong, et al. Sound transmission loss of metamaterial thin plates with periodic subwavelength arrays of shunted[J]. Journal of Sound and Vibration, 2015, 343: 104-120.

[19] ZHANG Hao, XIAO Yong, WEN Jihong, et al. Ultra-thin smart acoustic metasurface for low-frequency sound insulation[J]. Applied Physics Letters, 2016, 108(14): 1734.

[20] MEI J, MA G, YANG M, et al. Dark acoustic metamaterials as super absorbers for low-frequency sound[J]. Nature Communications, 2012, 3(2): 132-136.

[21] NAIFY C J, CHANG C M, MCKNIGHT G, et al. Membrane-type matamaterials: Transmission loss of multi-celled arrays[J]. Journal of Applied Physics, 2011, 109(10): 104902-104902-9.