金属蒙皮飞机冲击威胁研究

王守财， 关志东， 黎增山， 黄 骁

(北京航空航天大学 航空科学与工程学院, 北京 100191)

飞机在飞行与维修过程中，都可能受到外来物对机身蒙皮造成的冲击损伤，损伤的主要原因包括冰雹撞击，鸟撞以及维修工具坠落等[1]。冲击损伤严重影响了飞机的飞行安全，同时也对飞机的检修周期与维护成本提出了相应的要求，因此，对于飞机服役中所遭受冲击事件的研究就显得至关重要。

国外一项研究报告[2]指出，典型的飞行冲击损伤威胁与发生概率的数学描述形式为：

(1)

式中：Pj为冲击能量大于Ej的概率，x为与冲击威胁相关的系数。当x=3时，有：

Pj(E≥30 J)=10-5

/fh

(2)

对于某些冲击威胁较小的结构，x取值变小。

另一份研究报告[3]通过F-15机翼上得到的标定曲线，把金属结构上观察到的1 644个冲击凹坑转化成冲击能量水平，并得到了冲击能量上限约为48 J，且超越数-能量曲线的形状是对数线性的结论，其关系表达式为

lgPe=-x(j)/15

(3)

式中：Pe表示冲击能量中超过给定能量水平x(j)的概率。

国外一些航空公司也进行了相关的研究[4]，除了水平尾翼的内侧零件采用140 J的截止值以外，Airbus针对复合材料机身结构选择的能量截止门槛值是50 J；由于反映了美国空军要求和公司的设计准则，Boeing对民用飞机验证计划采用的能量截止值是136 J；Aerospatiale公司研究了意外冲击情况，采用36 J为其结构验证的能量截止门槛值。

国内本方面研究进行较少，王爱军等[5]认为结构受到的意外冲击威胁可以用冲击能量发生的概率来描述，并结合国外统计数据得到了一种冲击威胁的分布公式；冯振宇等[6]指出在不同文献中，冲击能量截止值的取值存在较大差异，并对不同文献中所取的冲击能量截止值进行了很好的归纳。文献[7]在论述冲击能量发生概率时指出，实际可能发生(发生概率≥10-5)的冲击能量水平应当不低于40 J。

尽管国内学者对冲击能量与发生概率之间的关系进行了较多的总结，但数据来源主要是国外研究机构已经公布的研究报告。由于飞行环境与维修人员身材的差异，有理由认为国内外飞机所面临的冲击损伤威胁是有区别的。而现代飞机面向全球市场，因此有必要整合不同地域冲击威胁数据，才能在设计中选取最合理的最大冲击能量作为参考。本文通过调研国内不同型号金属蒙皮飞机的飞行维修记录，对其损伤威胁分布规律进行统计，并估算金属蒙皮飞机在飞行中可能遇到的最大冲击能量，为其损伤检测以及维修周期的确定提供一定的数据支持。

1 损伤数据统计

本文采用概率性方法确定造成飞行损伤的最大冲击能量，用Pa表示飞机在某次飞行中受到冲击损伤，且能量大于一定冲击能量Ec的概率，P0表示飞机在某次飞行中受到冲击损伤的概率，Pe表示在遇到冲击事件的条件下，冲击能量大于Ec的概率。 可以认为是否受到冲击威胁与冲击能量大小无关，因此有：

Pa=Pe×P0

(4)

对南方某航空公司(以下简称来源1)与北方某飞机维修公司(简称来源2)近10年519架飞机的维修记录进行调研，总计获得8 656次损伤维修记录，经过进一步详细的筛选(损伤尺寸、损伤位置、飞机飞行小时信息完整)，挑选出有效数据1 006条，求得飞机在某次飞行中受到冲击事件发生损伤的概率，即P0，结果见表 1。

表1 低速冲击损伤发生的概率

数据来源1中飞机最大机龄16年，平均机龄7年，来源2中飞机最大机龄20年，平均机龄9年。损伤数据的另一项统计结果显示，随着使用年限的增加，低速冲击损伤呈现逐年上升的趋势，该原因也造成了两数据来源计算损伤概率的不同。综合两处来源的结果，预估冲击损伤概率为2.12×10-4/fh。其中机身损伤数据277条，机翼278条，冲击事件发生概率分别为5.857×10-5/fh与5.858×10-5/fh。

2 能量分布的确定

Pe表示在冲击事件中，冲击能量大于一定值的概率，为将已有的冲击损伤数据转化为冲击能量，需要建立冲击能量与损伤凹坑深度的关系。本文的研究思路为：对不同尺寸铝板进行数值仿真计算，用以对飞机不同区域的冲击响应进行模拟；然后进行单一尺寸铝板的低速冲击试验，对有限元模型的有效性进行验证。利用已经得到验证的有限元模型结果得到飞机不同区域冲击能量与损伤凹坑的拟合函数，从而达到由损伤逆推得到冲击能量的目的。

飞行遇到外来物冲击时，长桁提供载荷边界，查阅相关的飞机结构修理SRM手册，并结合调研损伤飞机型号，选取厚度2 mm，尺寸分别为180 mm×180 mm与250 mm×250 mm的7075-T6铝合金平板作为机身与机翼的试验对象。

2.1 数值仿真

2.1.1 材料本构模型

在黏弹性力学和连续介质损伤力学的基础上，考虑材料的大变形、高应变速率及温度影响的条件，Johnson和Cook提出了一个经验本构模型，该模型认为结构的等效应力可以表示为应变硬化、应变率硬化、以及热软化共同作用的结果

(5)

(6)

2.1.2 材料损伤演化模型

韧性材料的破坏主要有2种机理[11]：材料空隙聚集成核引起韧性破坏和局部剪切硬化引起剪切破坏。Hooputra等[12]针对这2种损伤机理，提出相应的损伤模型。

韧性破坏准则：

剪切破坏准则：

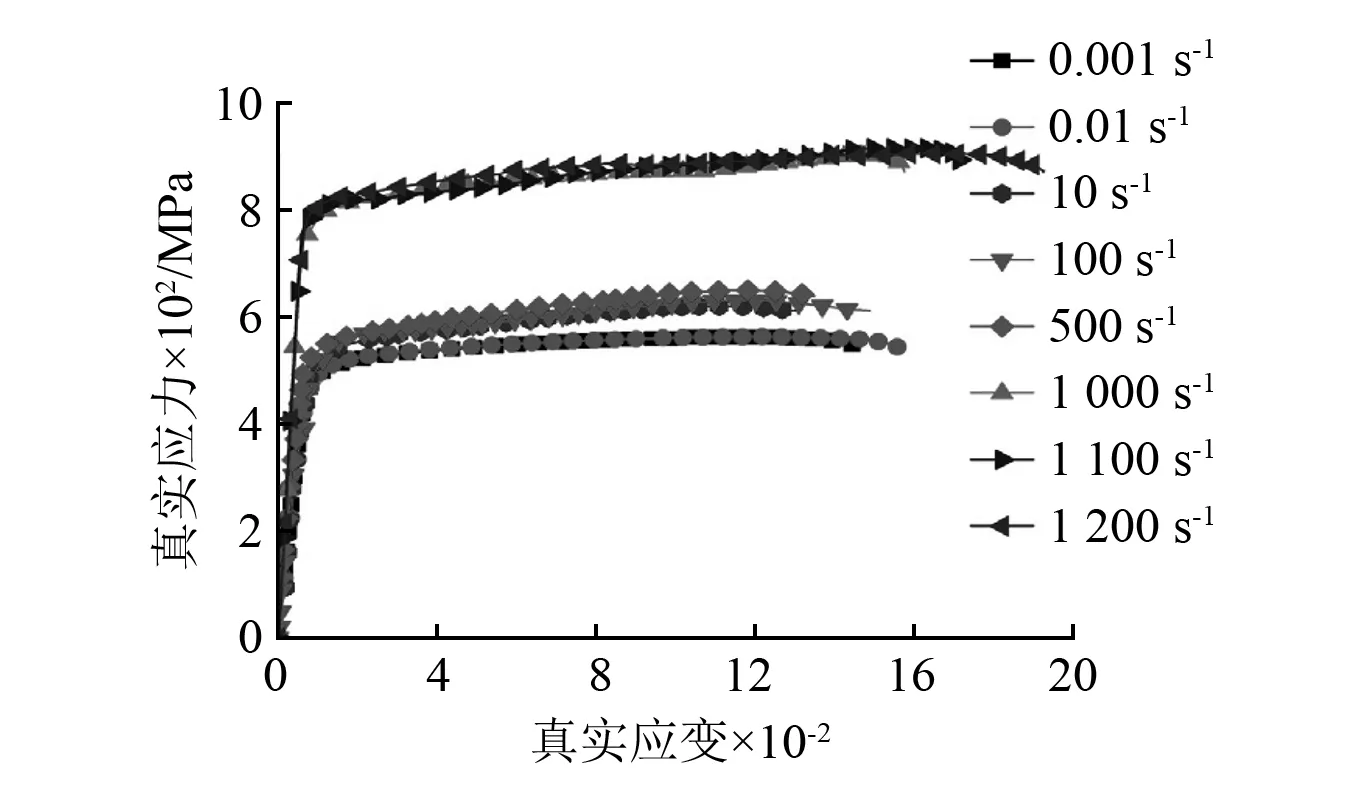
图1 7075-T6铝合金不同应变率应力-应变曲线Fig 1 Stress-strain curves of 7075-T6 aluminum alloy at different strain rate

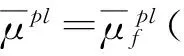
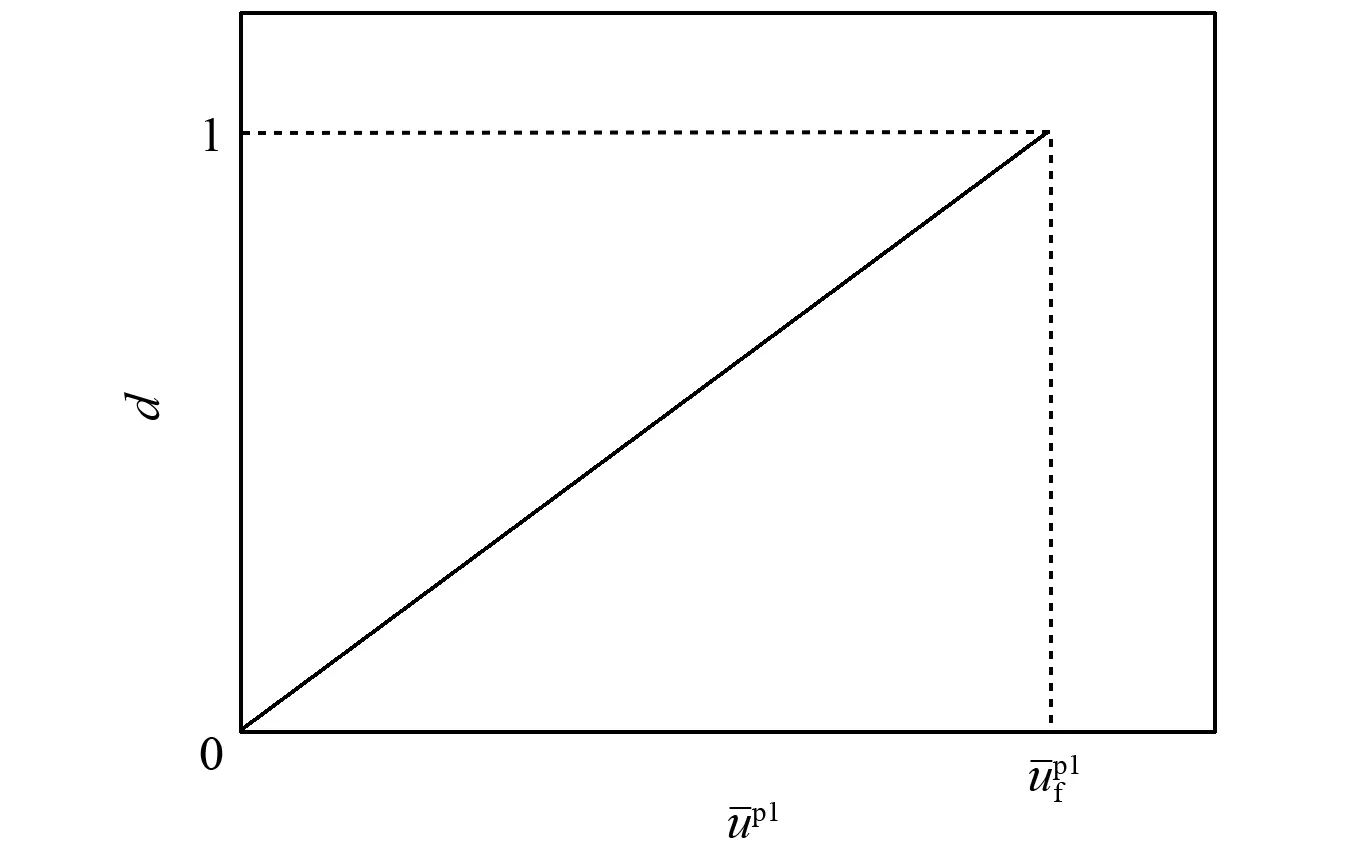
图2 铝合金材料线性损伤演化模型Fig 2 Linear damage propagation model of aluminum alloys materials

2.1.3 有限元模型建立

有限元模型如图 3所示，冲击试件采用八节点减缩积分单元(C3D8R),中心冲击区域网格加密，网格数量约12 000.铝板四周边界采用简支边界，冲头质量5.36 kg，直径25.4 mm，通过修改冲头速度改变冲击能量，7075-T6铝合金弹性参数，如表 2所示。

表27075-T6弹性参数

Tab.2 Elastic properties of 7075-T6 aluminum alloy

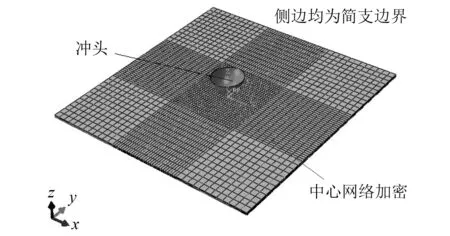
图3 有限元模型Fig.3 Finite element model

2.2 仿真结果与分析

图4为25 J冲击能量下，180 mm×180 mm铝板冲击点处接触力与铝板变形随时间的变化曲线。仿真结果显示，计算开始后冲头与铝板接触，后者在冲击作用下产生变形，并随时间增大；4 ms时，铝板变形达到最大，此时接触力亦为最大；4 ms之后，冲头回弹，变形与接触力变小；6.8 ms时，接触力变为0，冲头离开铝板，铝板震荡约0.5 ms左右变形稳定，留下永久塑性凹坑。但冲击能量较小，冲击铝板背面未产生裂纹。

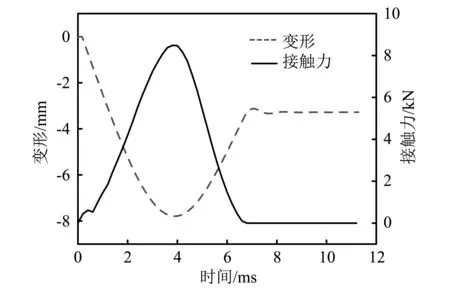
图4 冲击历程曲线Fig.4 Curves of the impact progress

根据数值仿真结果，冲击后铝板并不是只在冲击处产生凹坑，而是整个铝板都有一定程度的凹陷。为了对铝板的永久变形进行定量估计，一般定义[13]：dr为残余位移，其为冲击后平板的最大变形挠度；di为凹坑深度，其只是冲击区域的局部深度。凹坑深度稳定后冲击点剖面图见图 5。本文测量凹坑深度时，取变形稳定后冲击点中心位置与铝板边缘点坐标差作为冲击凹坑深度，从而使凹坑深度取得最大。

图5 冲击点剖面图Fig.5 The cross-section of impact point

对两种尺寸铝板低速冲击仿真结果见表 3，通过表中数据，可以得出，在相同的冲击能量下，尺寸较小的铝板更容易产生较大的凹坑。而拟合的结果也证明，在冲击能量较小，损伤凹坑较小时，冲击损伤凹坑深度与冲击能量大致呈线性，且两种尺寸的线性拟合结果分别为：

d=0.135Ebody+0.052

(7)

d=0.109Ewing-0.017 5

(8)

式中：d凹坑深度，Ebody，Ewing分别为机身与机翼的冲击能量，线性相关系数R2分别为0.993,0.996。

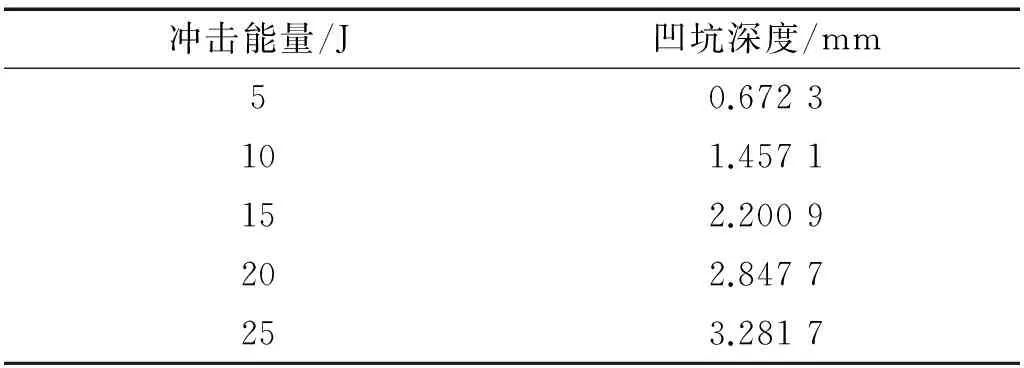
表3 铝板冲击仿真结果

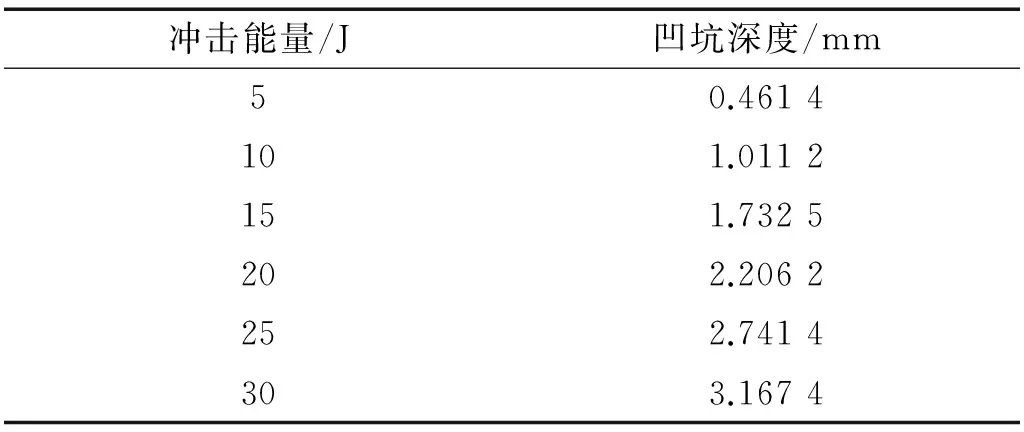
b 250 mm×250 mm

2.3 铝板低速冲击试验

为了证明上述模型的有效性，本文设计并执行了180 mm×180 mm铝合金平板的低速冲击试验。试验采用FC落锤式冲击试验机进行，试验机系统如图 6所示。考虑到蒙皮与桁条采用铆钉链接，试验铝板采用螺钉进行装夹，装夹情况如图 7所示。试验时将安装好的试件夹具整体固定在水平试验台上，通过调整落锤高度对试验件中心进行不同能量的冲击。冲击后通过人工方式对落锤阻止防止二次冲击。试验结束后立即使用精度为0.01 mm百分表对试验件中心凹坑深度进行测量，测量时在试验件远端进行调零，保证取到凹坑深度为最大值。

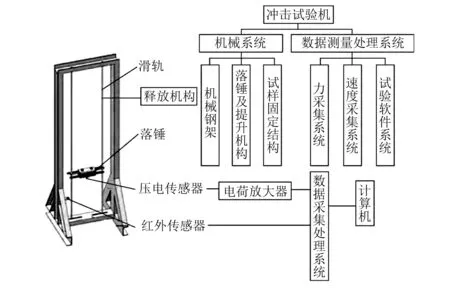
图6 FC落锤式冲击试验机[14]Fig.6 FC drop weight impact machine[14]

图7 试验件安装Fig.7 Fix of the specimen

按照有限元计算中选取的冲击能量，进行低速冲击试验，试验结果如表 4所示。表中相对偏差均为8%以下，考虑到凹坑深度本身值较小，因此在一定的精确范围内，可以认为有限元模型的计算结果是合理的。

表4 铝板冲击试验结果

2.4 Pe曲线的确定

对第1节中已经统计的低速冲击损伤与损伤数据表中ADL(允许损伤)进行统计，共有机身损伤368处，机翼损伤764处。利用2.2节中得到的凹坑深度与冲击能量的拟合函数，将该1 132条损伤数据转化为冲击能量。参考文献[3]中指出，飞机冲击能量与超越数成对数线性，分别对机翼与机身能量超越数概率取常用对数，结果如表 5表 6所示，冲击能量与超越数概率对数曲线拟合如图 8所示。

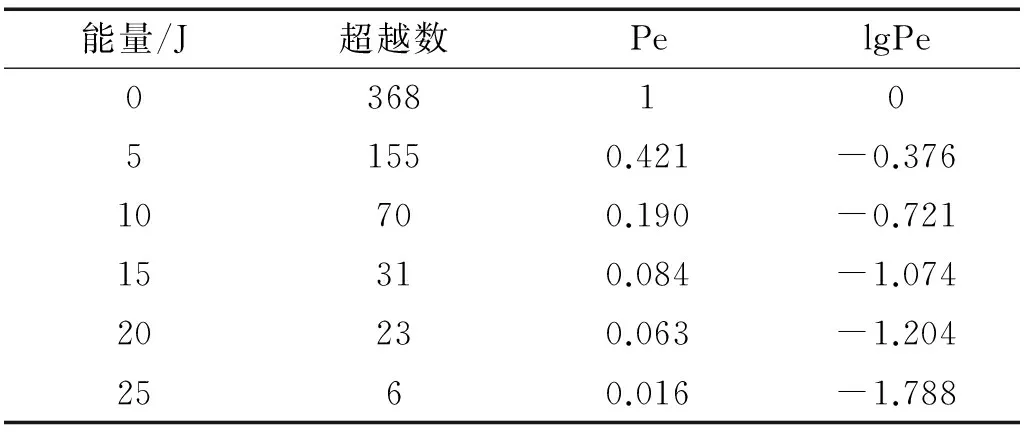
表5 冲击能量超越数(机身)

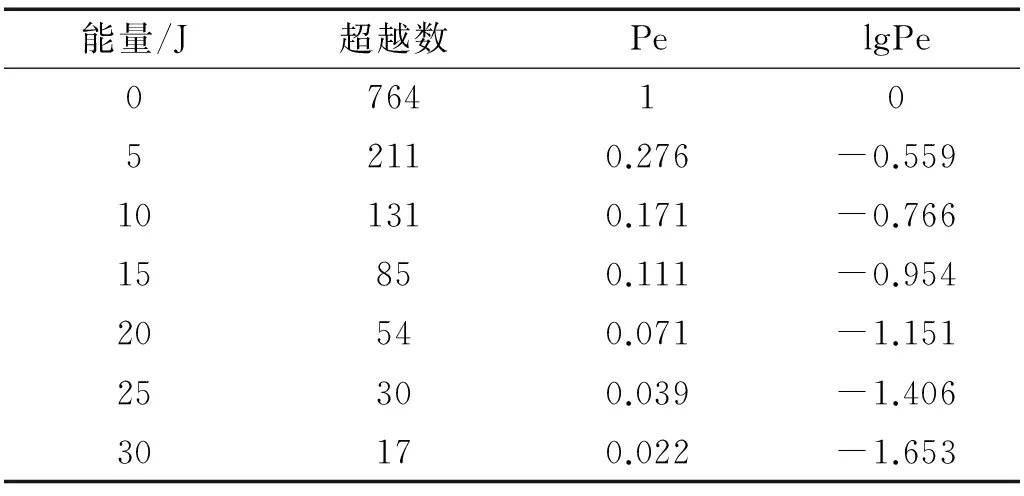
表6 冲击能量超越数(机翼)

图8 能量-lgPe 曲线Fig.8 The curves of energy-lgPe

对机身与机翼能量-超越数概率对数曲线进行线性拟合，线性相关系数分别为0.98与0.97，拟合结果进一步处理得到：

Pe, body=10-0.067E-0.019

(9)

Pe, wing=10-0.050E-0.173

(10)

式中：Pe, body为对机身造成损伤的冲击能量中，大于能量E的概率，Pe, wing为对机翼造成损伤的冲击能量中，大于能量E的概率。

将翼身能量数据合并，得到近似整机的能量超越数曲线，相关系数R2=0.98，拟合函数为：

Pe=10-0.056E-0.113

(11)

3 最大能量的确定

由Pa的定义可知，当Pa趋近于0时，表示Ec的发生概率很低，在一定的概率水平下可以认为是飞机飞行中所能遇到的最大能量。若在50 000飞行中，飞机至少有一次冲击能量大于Ec而产生损伤的概率为90%，则此时Pa为2.1×10-6；根据损伤事件发生调查统计结果，整体结构的损伤事件发生概率P0为2.12×10-4/fh，机身与机翼部分分别为5.857×10-5/fh 与5.858×10-5/fh，目前研究中一般将10-3/fh作为P0较为保守的取值，为了对统计结果与P0=10-3/fh进行计算对比，此时的对照计算结果，见表 7。

表7 Ec计算结果

可以得到结论：若根据损伤统计结果计算，机翼最大冲击能量大于机身，且二者均小于整机，分析原因是飞机机翼迎风面积较大，且维修时更容易对机翼造成损伤；而当P0均选择较保守的10-3/fh时，计算所得冲击能量均较统计结果偏大，按照该结果对结构进行设计，安全系数更高，但相应结构重量会较大。

4 结 论

本文基于调研所得飞机损伤数据，建立数值仿真模型与试验验证，逆推得到飞机冲击损伤能量分布。在逆推过程中，数值仿真与试验所用试件尺寸厚度依据飞机维修SRM手册，且考虑了蒙皮铆钉连接的边界条件。但由于外来物冲击方向的不确定性，采用垂直冲击确定冲击能量-凹坑曲线，会使得所求最大冲击能量结果较实际情况偏小。基于对以上误差的考虑，得到以下结论：

(1)本文所统计的飞行损伤数据中，冲击威胁发生的概率P0为2.12×10-4/fh，其造成的损伤大部分属于低速冲击损伤，而机翼与机身冲击威胁发生的概率相差不大，分别为5.857×10-5/fh与5.858×10-5/fh；

(2)建立了铝合金平板低速冲击仿真模型，计算结果与试验结果最大偏差小于8%；低速冲击载荷下，铝合金平板损伤凹坑与冲击能量可近似拟合为线性关系，且当厚度相同的铝板尺寸变大时，相同的冲击能量产生的凹坑变小；

(3)根据统计结果计算，当P0取2.1×10-6时，机翼、机身以及翼身整体受到的最大冲击威胁能量分别为21.3 J、25.5 J、33.8 J。

[ 1 ] 牛春匀. 实用飞机复合材料结构设计与制造[M]. 北京： 航空工业出版社， 2010.

[ 2 ] Development of Probabilistic Design Methodology for Composite Structure[R]. DOT/FAA/AR-96/111,1997.

[ 3 ] Advanced Certification Methodology for Composite Structures[R] . DOT/FAA/AR-96/111, 1997: 51-104.

[ 4 ] Department of the defense United State of America MIL-HDBK-17F composite materials handbook[S]. Polymer Matrix Composites Material Usage, Design and Analysis, 2002.

[ 5 ] 王爱军，李强，陈普会. 民用飞机复合材料结构损伤容限的概率分析方法[C].第17届全国复合材料学术会议， 2012.

[ 6 ] 冯振宇，郝鹏, 邹田春. 复合材料结构损伤容限设计中的两个关键参数[J]. 材料导报， 2011, 25(18): 242-244.

FENG Zhenyu, HAO Peng， ZOU Tianchun. Two critical parameters in composite structure damage tolerance design [J]. Materials Review, 2011, 25(18): 242-244.

[ 7 ] 沈真, 张子龙, 王进, 等. 复合材料损伤阻抗和损伤容限的性能[J]. 复合材料学报，2004, 21(5): 140-145.

SHEN Zhen, ZHANG Zilong, WANG Jin, et al. Characterization of damage and damage tolerance of composite laminate [J]. Acta Materiae Composite Sinica, 2004, 21(5): 140-145.

[ 8 ] ZHANG D N，SHANGGUAN Q Q，XIE C J，et al． A modified Johnson-Cook model of dynamic tensile behaviors for 7075-T6 aluminum alloy [J]. Journal of Alloys and Compounds， 2015, 619: 186-194.

[ 9 ] 谢灿军，童明波，刘富，等. 民用飞机平尾前缘鸟撞数值分析及试验验证[J].振动与冲击，2015，34(14):172-178.

XIE Canjun, TONG Mingbo, LIU fu, et al. Numerical analysis and experimental verification of bird impact on civil aircraft’s horizontal tail wing leading edge [J]. Journal of Vibration and Shock, 2015, 34(14): 172-178.

[10] 刘富，张嘉振，童明波，等. 2024-T3 铝合金动力学实验及其平板鸟撞动态响应分析[J]. 振动与冲击， 2014， 33(4)： 113-118.

LIU Fu, ZHANG Jiazhen, TONG Mingbo, et al. Dynamic tests and bird impact dynamic response analysis for a 2024-T3 aluminum alloy plate [J]. Journal of Vibration and Shock, 2014, 33(4): 113-118.

[11] 徐荣章，关志东，蒋思远.侧边边界条件对铝合金加筋板轴压性能的影响[J]. 北京航空航天大学学报, 2016, 42(1): 187-192

XU Rongzhang, GUAN Zhidong, JIANG Siyuan. Influence of side boundary condition on compression performance of aluminum alloys stiffed panels [J]. Journal of Beijing University of Aeronautics And Astronautics, 2016, 42(1): 187-192.

[12] HOOPUTRA H, ESE H, ELL H, et al. A comprehensive failure model for crashworthiness simulation of aluminum extrusions [J]. International Journal of Crashworthiness, 2004, 9(5): 499-463.

[13] 马玉娥，胡海威，熊晓枫. 低速冲击下FMLs、铝板和复合材料的损伤对比[J]. 航空学报， 2014, 35(7): 1902-1909.

MA Yue, HU Haiwei, XIONG Xiaofeng. Comparison of Damage in FMLs, Aluminium and composite Panels Subjected to Low-velocity Impact [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1902-1909.

[14] 冀赵杰，关志东，黎增山. 低速冲击下复合材料加筋板的损伤阻抗性能[J]. 北京航空航天大学学报， 2016， 42(4)： 751-761.

JI Zhaojie, GUAN Zhidong, LI Zengshan. Damage resistance property of stiffened composite panels under low-velocity impact [J]. Journal of Beijing University of Aeronautics and Astronautics, 2116, 42 (4): 751-761.