基于模糊控制的前轮转弯控制律设计

赵 喆， 贾玉红， 田剑波

(1. 上海飞机设计研究院 液压系统设计研究部，上海 201210； 2. 北京航空航天大学 航空科学与工程学院，北京 100083； 3. 上海飞机设计研究院 科学技术委员会，上海 201210)

大型民用客机起落架系统多采用多轮多支柱布局[2-3]。飞机地面操纵稳定性直接影响飞机起降以及滑行阶段的性能及安全[3]，相关方面研究一直受到国内外研制单位及客户的高度重视[4-6]。随着起落架系统需求及性能指标的不断提高、科技的不断进步发展，更多新的技术逐步应用于飞机地面操纵稳定性设计领域[7-9]。

模糊控制多采用语言变量和模糊集合理论形成控制算法, 适合非线性、时变、滞后、模型不完全系统, 具有较佳的鲁棒性(Robustness)、适应性及容错性(Fault Tolerance)[10-15]。

为研究支柱小车式布局的起落架系统在地面低速滑行阶段转弯时前轮和主轮的侧滑稳定性，现对采用复杂布局小车式布局的起落架系统进行动力学分析，并基于模糊控制理论设计一套前轮转弯角速度控制律，以期提高复杂布局小车式起落架系统在地面低速转弯时的操纵性能。

1 起落架系统动力学分析

1.1 假设及定义

(1) 用飞机重心轨迹代替飞机运动轨迹；

(2) 用飞机运动的瞬时中心代表飞机运动轨迹的曲率中心，忽略瞬时中心自身加速度影响；

(3) 轮胎为刚性轮胎；

(4) 飞机在滑跑阶段油门始终维持在特定位置；

(5) 不采用发动机差动转弯；

(6) 不采用主轮差动刹车转弯。

1.2 复杂布局小车式起落架地面动力学特性分析

飞机地面运动可认为是飞机保持重心高度不变，作平行于地面的平面运动。飞机的这种平面运动可简化为平动和转动的合成运动：

(2) 基点T.C在全局坐标系中所作的平动运动(牵连运动)。

由于多轮多支柱起落架国外各公司均依据各自的标准进行设计与生产，因而仍未形成一个可供设计人员参考、执行的通用标准或行业规范。因此，如图1所示，现认为复杂布局小车式布局的起落架系统主动转弯时，机轮运动情况如下：前轮(N.G)主动转弯，机翼主轮(W.G)固定，机身主轮(B.G)随动转弯，五套机轮的基点(T.C，瞬时转动中心)重合。

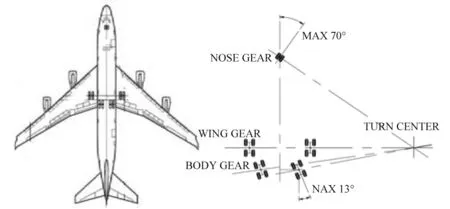
图1 复杂布局小车式起落架布局Fig.1 A layout of Multiple-bogie Undercarriage

1.2.1 笛卡尔坐标系下的动力学分析

在笛卡尔坐标系下，简化的复杂布局小车式起落架动力学模型如图2所示，其他相关动力学参数如图3所示。其中：O1/C.G为重心；W为飞机瞬时转动中心在飞机中心线上的垂足；α1为前轮偏转角；α2为左机身主轮偏转角；α3为右机身主轮偏转角；β为重心速度与飞机中心线夹角；σ为飞机偏转角；FE为发动机推力；FG为飞机航向空气阻力；NN为前轮侧向力；TN为前轮滚动摩擦阻力；NW为机翼主轮侧向力；TW为机翼主轮滚动摩擦阻力；NB1为左侧机身主轮侧向力；TB1为左侧机身主轮滚动摩擦阻力；NB2为右侧机身主轮侧向力；TB2为右侧机身主轮滚动摩擦阻力；a为飞机重心站位至前轮站位的距离；b为飞机重心站位至机翼主轮站位的距离；c为机翼主轮至机身主轮站位的距离；e为前起落架稳定矩；r为飞机瞬时转动中心在飞机中心线上的距离；B1为机身主轮间距；B2为机翼主轮间距；RN为前轮垂向载荷；RW为机翼主轮垂向载荷；RB为机身主轮垂向载荷；l1为前起落架空载高度；l2为机翼主起落架空载高度；l3为机身主起落架空载高度；k1为前起落架缓冲器刚度系数；k2为机翼主起落架缓冲器刚度系数；k3为机身主起落架缓冲器刚度系数。

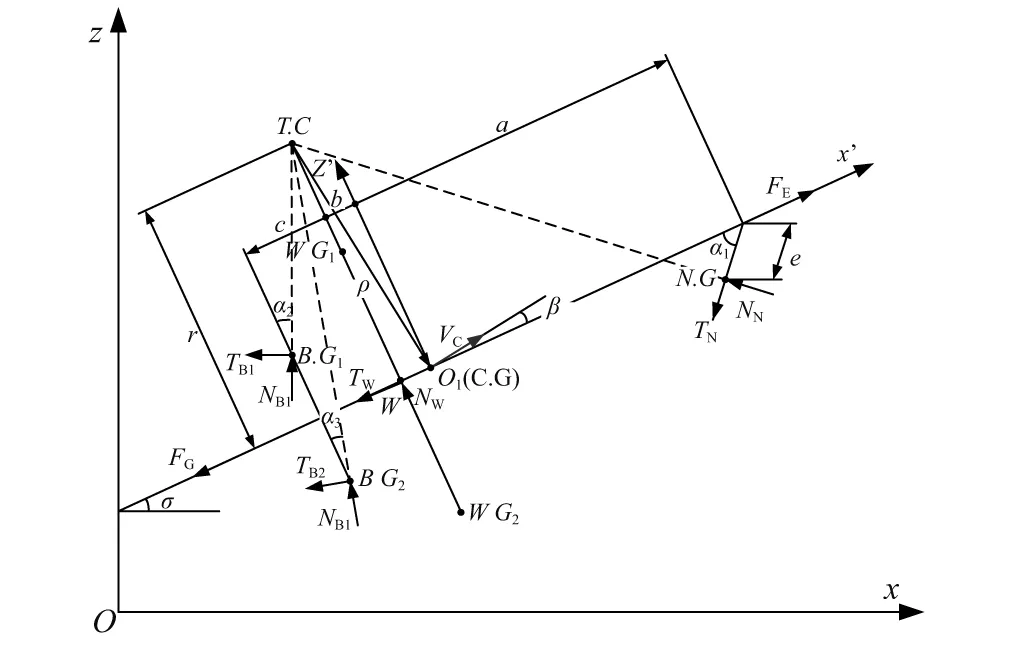
图2 笛卡尔坐标系下复杂布局小车式起落架系统简化动力学模型Fig.2 A simplified kinetic model of multiple-bogie undercarriage system in cartesian coordinates

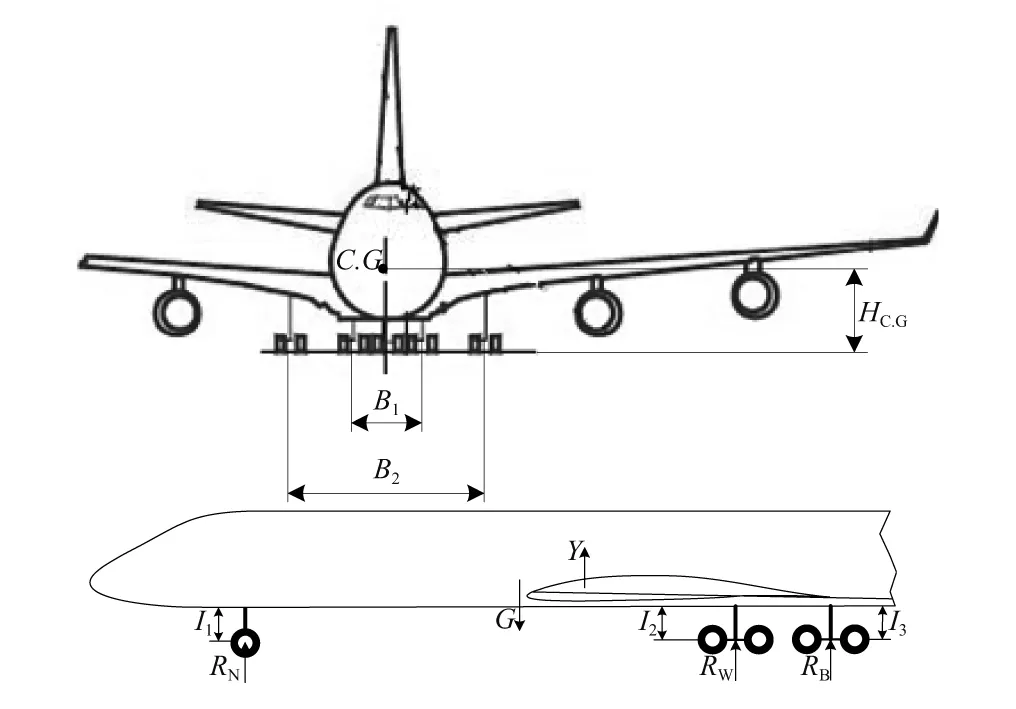
图3 其他相关动力学模型参数Fig.3 Other parameters of the kinetic model

(1) 飞机的载荷分析

① 飞机沿O1X′方向所受载荷

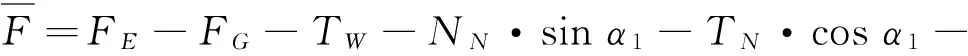
(1)

② 飞机沿O1Z′方向所受载荷：

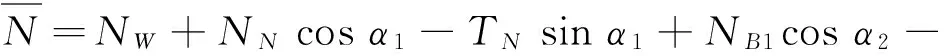
(2)

RN·a-RW·b-RB·(b+c)=0

(3)

③ 飞机沿O1Y′方向所受载荷：

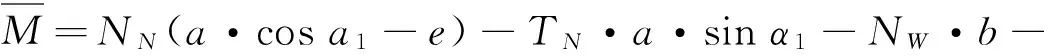
(4)

RN+RW+RB+Y-G=0

(5)

(2) 飞机的地面运动分析

① 飞机沿O1X′方向运动情况分析：

(6)

(7)

② 飞机沿O1Z′方向运动情况分析：

(8)

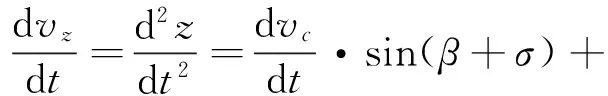
(9)

③ 飞机沿O1Y′方向运动情况分析：

(10)

(11)

(3) 飞机的动力学分析

① 飞机沿O1X′方向动力分析：

(12)

② 飞机沿O1Z′方向动力分析：

(13)

③ 飞机在O1Y′点力矩分析：

(14)

④ 几何关系：

(15)

(16)

(17)

(18)

(19)

1.2.2 欧拉坐标系下的动力学分析

在欧拉坐标系下，简化的复杂布局小车式起落架动力学模型如图 4所示。其中：J为飞机沿O1Y′方向过重心轴线的转动惯量；ρ为重心处的转弯半径。

图4 欧拉坐标系下复杂布局小车式起落架系统简化动力学模型Fig.4 A simplified kinetic model of multiple-bogie undercarriage system in Eulerian coordinates

(1) 飞机重心沿法线方向动力学分析：

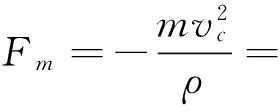
(20)

(2) 飞机重心沿切线方向动力学分析：

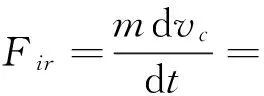
(21)

(3) 飞机在速度瞬心处力矩分析：

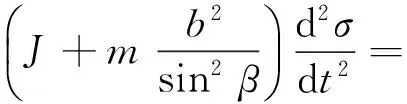
(22)

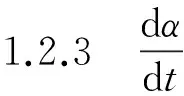
联立公式(7)以及公式(9)可得：

(23)

联立公式(12)以及公式(13)可得：

(24)

(25)

联立公式(11)以及公式(14)可得：

(26)

则：

(27)

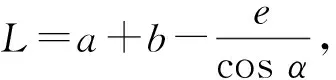
(28)

(29)

(30)

1.2.3RN、RW以及RB的表达式

联立公式(3)、公式(5)以及公式(19)可得：

G·r=c

(31)

其中：

(32)

r=(RNRWRB)T

(33)

(34)

令：

(35)

则：

(36)

(37)

(38)

1.3 飞机地面低速运动时不发生侧滑的临界条件

将式(4)、式(11)以及式(14)代入式(22)，则：

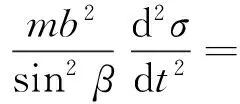
(39)

令：F0=FE-FG-TW，联立式(20)、式(21)以及式(39)，可得：

A·n=m

(40)

其中：

A=(a1a2a3a4)

(41)

n=(NNNWNB1NB2)T

(42)

m=(m1m2m3)T

(43)

(44)

(45)

(46)

(47)

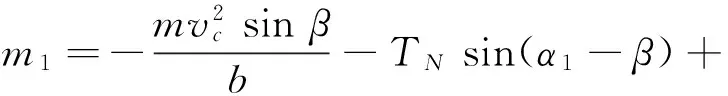
(48)

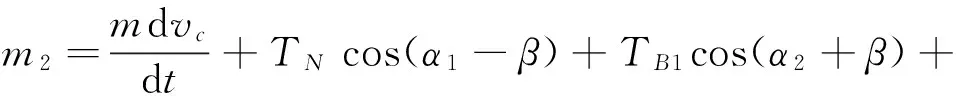
(49)

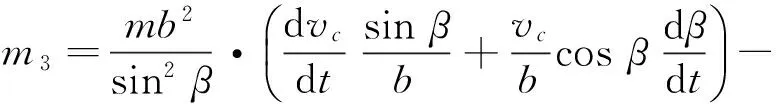
(50)

令：

A1=(a1a2a3)

(51)

n1=(NNNWNB1)T

(52)

则：

A1n1=m-NB2a4

(53)

(54)

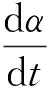
(55)

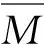
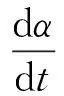
(56)

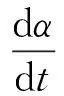
(57)

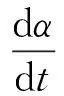
(58)

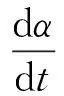
(59)

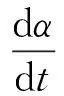
(60)

令轮胎的极限侧向摩擦力为NL,C， 根据许多试验结果表明，当机轮偏转角α<12°～15°时， 轮胎极限侧向摩擦力NL,C可表达为：

(61)

当a>12°～15°时， 轮胎的极限侧向摩擦力NL,C可表达为：

(62)

以上，RST为机轮停机载荷，R为机轮径向载荷，μL,S为轮胎侧向摩因数[1]。

飞机不发生侧滑的条件为：

N≤NL,C

(63)

(64)

1.4 飞机前轮转弯许用角速度的影响因素

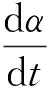
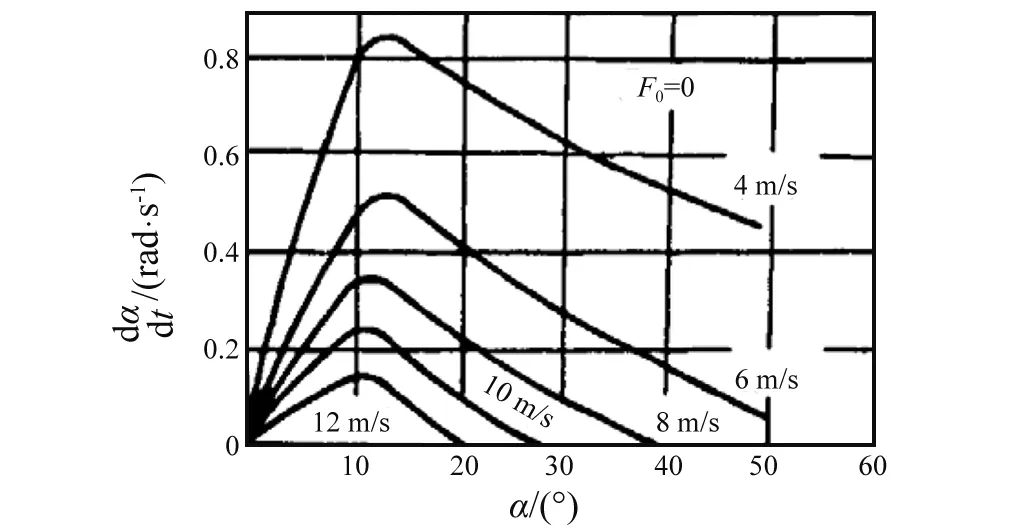
图5 F0=0时，随Vc以及α变化的许用曲线Fig.5 Allowable curve of changing with Vc and α, when F0=0

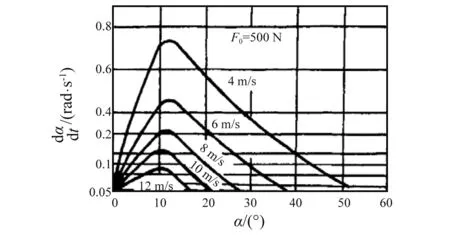
图6 F0=500 N时，随Vc以及α变化的许用曲线Fig.6 Allowable curve of changing with Vc and α, when F0=500 N

不难发现：

2 飞机地面低速运动的模糊控制

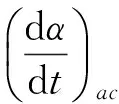
图7 使用操纵角速度的确立Fig.7 Establishment of actual steering rate

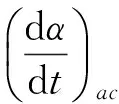
为解决上述问题，现基于模糊控制理论设计一套控制律，以优化前轮转弯实现方式，提高起落架系统在地面低速转弯时的操纵性能。

2.1 模糊控制器结构

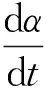
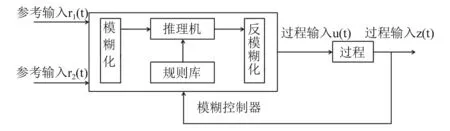
图8 模糊控制器Fig.8 Fuzzy controller

2.2 模糊控制器的规则库

(1) 操纵角度α1

NL：飞机沿逆时针方向产生“大”角度偏移；

NS：飞机沿逆时针方向产生“较大”角度偏移；

ZO：飞机在“中立”位置；

PS：飞机沿顺时针方向产生“较大”角度偏移；

PL：飞机沿顺时针方向产生“大”角度偏移。

(2) 飞机质心速度Vc

NL：飞机“静止”；

NS：飞机“慢速”前进；

ZO：飞机“较慢”前进；

PS：飞机“较快”前进；

PL：飞机“快速”前进。

NL：飞机沿逆时针方向“快速”转弯；

NS：飞机沿逆时针方向“较快”转弯；

ZO：飞机“停止”转弯；

PS：飞机沿顺时针方向“较快”转弯；

PL：飞机沿顺时针方向“快速”转弯。

飞机前轮偏转角速度与前轮偏转角度、飞机速度对应的控制规则如表1 所示。

表1 模糊控制规则库

前轮操纵模型控制变量的隶属度函数分别如图9～图11所示。

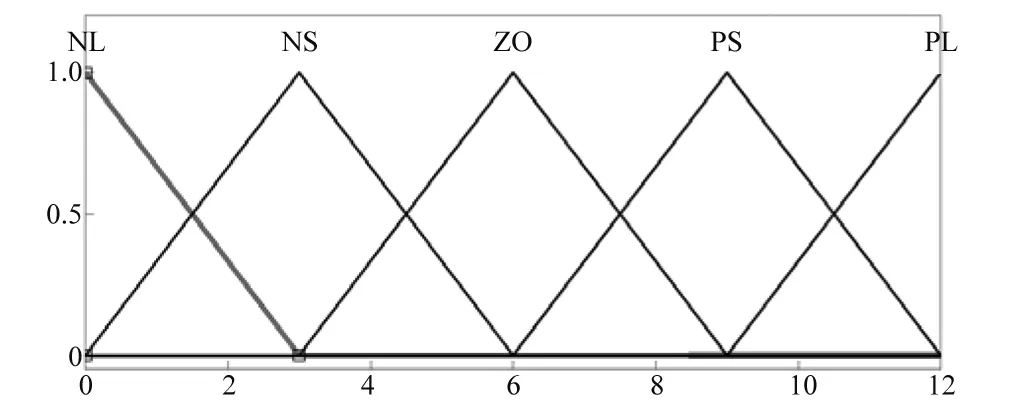
图9 Vc隶属度函数Fig.9 Subjection function of Vc

令μ为输出影响因子，在不同输入变量作用下，采用“取小原则”确立控制规则，即：

μpre=min{μ1,μ2}

(65)

将推理结果转换成实际作用，即：

图10 α1隶属度函数Fig.10 Subjection function of α1

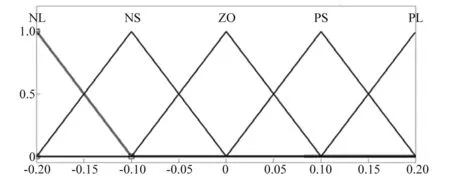
图隶属度函数图Fig.11 Subjection function of

(66)

生成控制律曲面如图12所示。

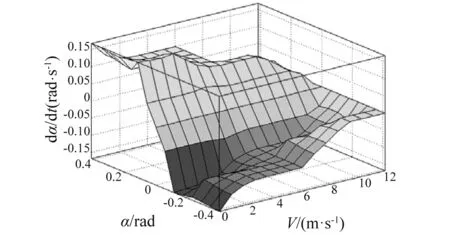
图12 控制律曲面Fig.12 Control law surface

3 模拟仿真

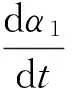
(1) 如图14所示，基于模糊控制理论的前轮转弯角速度控制律有以下特征：①前轮偏转角度一定时，随着飞机速度增加，前轮偏转角速度不断减小。②飞机速度一定时，随着飞机操纵角的不断增加，前轮偏转角速度先增加后减小。

图13 基于模糊控制理论的前轮控制律仿真Fig.13 Simulation of nose wheel steering control law based on fuzzy control theory

(2) 如图15所示，基于模糊控制的前轮偏转角速度控制率与前轮许用偏转角速度包线比较：①基于模糊控制的前轮偏转角速度控制率变化趋势与前轮许用偏转角速度变化趋势一致。②经调参优化后的基于模糊控制的前轮转弯角速度控制率可与前轮许用偏转角速度包线较好贴合，充分发掘起落架系统地面运动能力。

(3) 如图16所示，当飞机速度为8 m/s时，前轮由0.07 rad偏转到0.24 rad时：①使用传统控制律，系统响应时间为3.5 s。②使用基于模糊控制理论的前轮转弯角速度控制率，系统响应时间为2.75 s。③相对于传统控制律，基于模糊控制理论的前轮转弯角速度控制律可较快完成前轮偏转作动，转弯效率可提升27.3%。

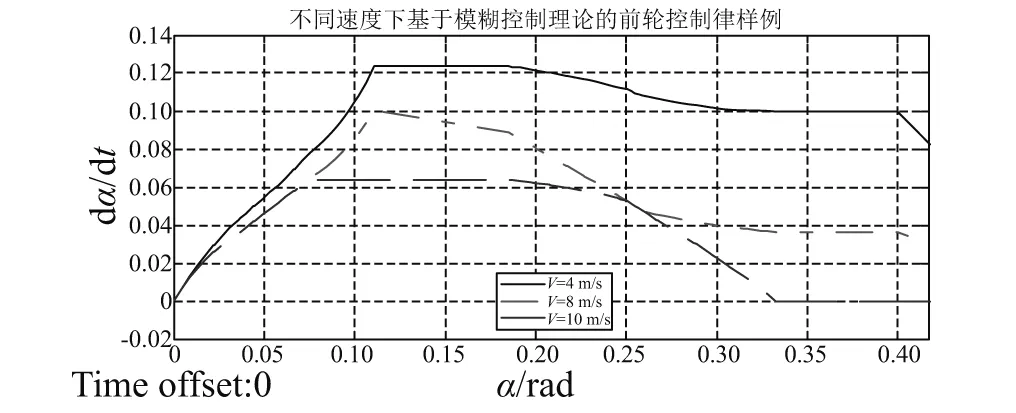
图14 不同速度下基于模糊控制理论的前轮控制律样例Fig.14 Samples of nose wheel steering control law based on fuzzy control theory, on different AC speed

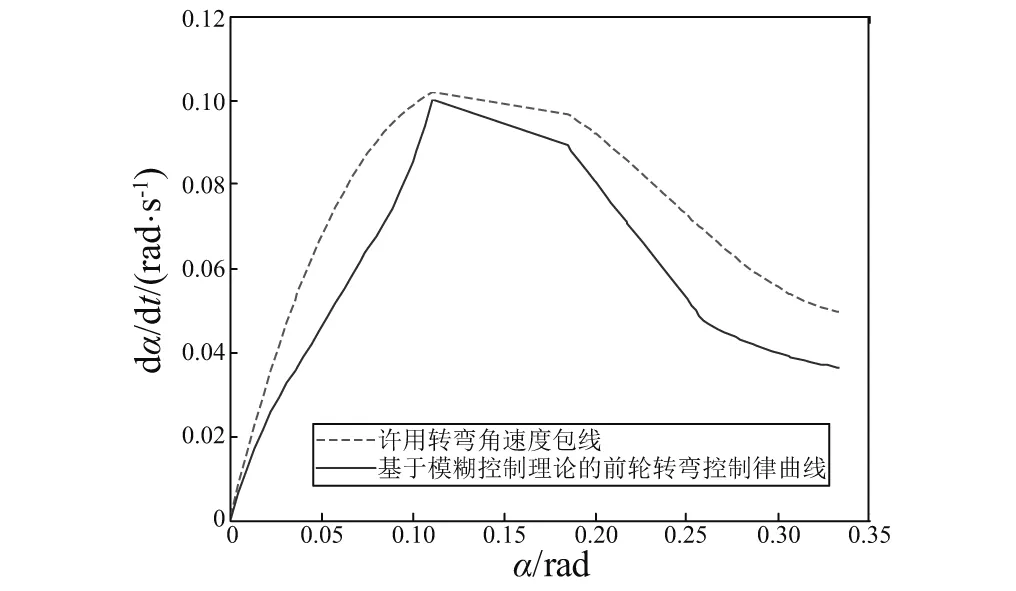
图15 基于模糊控制理论的前轮控制律与前轮转弯许用角速度包线的对比Fig.15 A comparison of nose wheel steering control law based on fuzzy control theory and the envelope of allowable nose wheel steering rate

图16 基于模糊控制理论的前轮转弯控制律与传统前轮转弯控制律对比Fig.16 A comparison of nose wheel steering control law based on fuzzy control theory and traditional nose wheel steering control law

4 结 论

(2) 在不改变飞机构型、不影响飞机性能及安全性的前提下，可通过降低飞机速度及发动机推力等方式提高起落架系统许用前轮转弯角速度。

(3) 基于模糊控制理论的前轮转弯角速度控制律与前轮转弯许用操纵角速度包线的变化趋势相符合，验证了模糊控制理论应用于飞机前轮转弯角速度控制律设计的可行性。

(4) 基于模糊控制理论的飞机前轮转弯角速度控制律可较好与许用转弯角速度包线拟合，充分发掘起落架系统地面运动能力。

(5) 相对于传统前轮转弯控制律，基于模糊控制理论的前轮转弯角速度控制律可显著提升起落架系统地面操纵性能。

[ 1 ] 高泽迥,黄振威,等.飞机设计手册,第14册,起飞着陆系统设计 [M].北京:航空工业出版社, 2002: 38-79.

[ 2 ] CURREY S N. Aircraft landing gear design: principles and practices[M]. 4th ed.Washington D.C.:AIAA,1988: 7-31.

[ 3 ] 聂宏,魏小辉.大型民用飞机起落架关键技术[J]. 南京航空航天大学学报, 2008, 40(4): 427-432.

NIE Hong, WEI Xiaohui. Key technologies for landing gear of large civil aircrafts[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 427-432.

[ 4 ] SIVARAMAKRISHNAN M M. Influence of landing gear flexibility on aircraft performance during ground roll[J]. Journal of Aircraft, 1981,18(11): 991-992.

[ 5 ] PRITCHARD J. Overview of landing gear dynamics[J]. Journal of Aircraft, 2001,38(1): 130-137.

[ 6 ] PRASHANT D K. Simulation of asymmetric landing and typical ground maneuvers for large transport aircraft[J]. Aerospace Science and Technology, 2003,7(8): 611-619.

[ 7 ] ROUNDHILL J. The future of commercial aviation, building on our legacy, AIAA-2003-2552[R]. Dayton, Ohio: 2003.

[ 8 ] JARRY P. The future of commercial aviation, airbus view, AIAA-2003-2553[R]. Dayton, Ohio: 2003.

[ 9 ] HOWCROFT C, LOWENBERG M, NEILD S. Shimmy of an aircraft main landing gear with geometric coupling and mechanical freeplay[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(5): 051000.

[10] RAJU G V S, ZHOU J. Adaptive hierarchical fuzzy controller[J]. IEEE Transaction on System, Man and Cybernetics, 1993,23(4): 973-980.

[11] HUANG S, LIN C. Application of a fuzzy enhance adaptive control on active suspension system[J]. International Journal of Computer Application in Technology, 2004,20(4): 152-160.

[12] AI-HOLOU N. Sliding mode neural network inference fuzzy logic control for active suspension system[J]. IEEE Transactions on Fuzzy System, 2002,10(2): 234-246.

[13] 王丕宏,高金源,杨克明. 飞机大机动飞行的一种模糊控制系统设计方法[J]. 北京航空航天大学学报, 2000, 26(5): 513-515.

WANG Pihong, GAO Jinyuan, YANG Keming. Design method of fuzzy system to control large maneuver flight of aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(5): 513-515.

[14] BOUOUDEN S, CHADLI M, KARIMI H R. A robust predictive control design for nonlinear active suspension systems[J]. Asian Journal of Control, 2016,18(1): 122-132.