基于SNGR方法研究增升装置缝翼噪声的抑制效果

余培汛， 潘 凯， 白俊强， 韩 啸

(1. 中国飞机强度研究所 航空声学与动强度航空科技重点实验室，西安 710065； 2. 西北工业大学 航空学院，西安 710072)

在现代大型运输机的设计过程中，气动噪声是一个不可忽略的重要问题，而运输机的机体噪声在整个飞机噪声中占着非常大的一个比例。飞机在起飞和降落过程中，需要打开增升装置起到提供高升力的作用，与此同时其复杂的机构易引起强烈的气动噪声问题，这严重影响了机场附近的居民生活和乘客的舒适性。因此，增升装置的气动噪声抑制问题在当今航空领域也是一个研究热点。

由于机翼分段、缝隙、空腔以及展向剪刀差的存在，增升装置流动复杂，有分离涡产生，有尾迹与附面层汇流，而增升装置构型的调整及缝道参数的微小改变，均可能引起整个湍流场的改变，进而影响到整个声场。Ewert等[1]基于随机粒子网格法(FRPM)的CAA方法计算分析了三段翼缝翼的气动噪声问题，其计算结果与AWB试验结果趋势非常吻合。Fosso Pouangue等[2]采用基于RANS的经验公式对L1T2高升力翼型进行了低噪声的优化设计，结果表明通过该方法设计出的高升力翼型相比于基准构型的噪声更小，且升力更高。Grundestam等[3]耦合RANS/LES与Kirchhoff的方法，通过计算对比分析了不同增升装置形式的噪声问题，并探索噪声与当地流场参数间的关系。Wang等[4]采用脱体涡数值模拟方法研究了高升力装置的缝翼滑轨对其噪声的影响，结果表明缝翼滑轨可以有效的降低缝翼处的噪声源。Molin等[5]耦合RANS/LES与FWH方程的方式对缝翼产生的气动噪声问题进行了预测分析。Guo等[6]依据风洞试验的结果，建立了增升装置的气动噪声物理模型，并对MD-11等构型的增升装置进行了预测分析。此外，在增升装置噪声预测和减噪技术研究方面的国外学者还有Reiche等[7]，Streett等[8]，Yokokawa[9]，Murayama[10]。而在增升装置气动噪声预测方面，国内相对研究较少。其中，南京航空航天大学的吕宏强等[11]基于高阶间断有限元的线化欧拉方程进行了多段翼型的气动噪声预测分析。卢清华等[12]基于LES/FWH的方法研究了增升装置的气动噪声特性，结果表明：缝翼噪声主要是由于流动在缝翼和主翼之间的凹槽形成的不稳定波以及缝翼钝后缘的小脱落涡造成的。乔渭阳等[13]指出飞机襟翼侧缘噪声谱中的单音噪声是来自于襟翼侧缘涡的不稳定振荡，而襟翼侧缘宽频的噪声信号是由于在襟翼侧缘处气流强烈的湍流脉动与襟翼侧缘复杂的后缘结构的相互干涉所产生的。

针对增升装置缝翼的气动噪声问题，本文基于随机湍流脉动速度生成模型的SNGR(Stochastic Noise Generation and Radiation)方法开展了研究。通过改变缝翼的几何形状，分析其对缝翼噪声的抑制效果。研究结果表明：通过延长缝翼前缘的几何形状能有效增强缝翼来流剪切层的稳定性，达到抑制缝翼噪声的效果。

1 数值模拟方法

1.1 线化欧拉方程

文中的声学传播方程采用了带源项的线化欧拉方程，其在直角坐标系下可写成如下形式：

(1)

式中：Q为守恒变量；E，F，G为对流项；S为声源项。具体表达形式为：

1.2 湍流脉动速度人工重构

Kraichnan等[14]提出通过有限个模态相叠加的方法来模拟空间统计湍流速度场。Bailly等在Karweit方法的基础上，通过引入湍流速度的时间相关性，以及对流影响，对湍流速度场进行了修正。其具体形式如下：

(2)

式中：Uc指当地对流速度，un、ψn、σn分别表示波数空间中第n阶模态的幅值、相位和指向。如图1所示，在波数空间中，ψn、φn、an均为取值范围为[0,2π]的随机数，θn为取值范围[0,π]的随机数。

由不可压缩各向同性湍流的能量传输关系式可推导出波数矢量kn与指向σn相互垂直。ωn为符合高斯概率密度函数分布的第n阶模态的角频率：

(3)

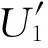
(4)

本文选用了各向同性的Von Karman-Pao能谱，如图2所示。其具体表达式如下：

(5)

式中：kη=ε1/4υ-3/4是Kolmogorov尺度的倒数。参数A为常数，ke为Von Karman-Pao能谱中最大波数。

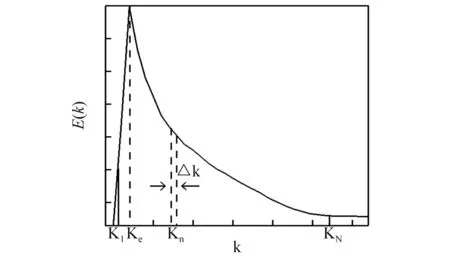
图2 Von Karman-Pao能谱Fig.2 Von Karman-Pao Energy spectrum

总湍动能可表示为在波数域内能量的积分形式：

(6)

常数A由下面的公式确定：

(7)

[15]，可知ke表达式：

(8)

其中L、Λ11的表达式分别如下：

(9)

(10)

式中：fL为常系数； 根据参考文献[15]的设置，本文取1。

能谱E(k)可采用线性分布和指数分布两种形式进行分解，为了能在小波数范围内更好的解析能谱，文中采用了指数分布的形式：

(11)

kn=exp[ln(k1)+(n-1)·d]，n=1,2,…,N

(12)

式中： 可取k1=kemin/5，kN=2π/(6Δx)。kemin表示声源区域内ke的最小值，N取100。

2 计算方法可靠性验证

本节主要是采用SNGR方法来进行缝翼噪声的预测分析，并判断该方法在缝翼噪声的预测分析中是否合理有效。计算对象为30P30N三段翼模型，马赫数Ma=0.17，迎角Alpha=4°，单位尺度雷诺数Re=3.72E+006，参考长度L=0.457。声传播方程的空间离散采用7点4阶的DRP格式，时间推进选用了高精度大时间步长的6级4阶龙格库塔格式，远场边界应用了无分裂形式的理想匹配层边界条件。声场计算全场统一采用无量纲时间步长Δt=0.000 1。

计算中所涉及到的CFD网格和CAA网格分别如图3(a)、(b)所示。CFD网格量1 064 356，附面层第一层网格长度为1E-006，以1.05倍比例向外增长，缝翼表面分布了383个网格点，主翼表面分布了675个网格点，襟翼表面分布了196个网格点。而CAA网格量2 425 924，最小网格尺度0.001，缝翼、主翼、襟翼表面的网格分布与CFD分布类似，其附面层向外增长的比例几乎呈现等均分布。图4给出了缝翼处CFD网格的湍动能信息赋值给CAA网格的对比结果，两者在分布位置和量级保持高度一致。从图4的插值结果可以说明所采用的流场与声场传递信息的方法具备处理复杂网格的能力。

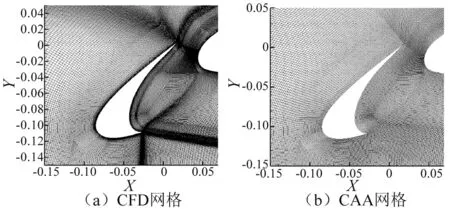
图3 计算网格示意图Fig.3 Diagram of computational grid

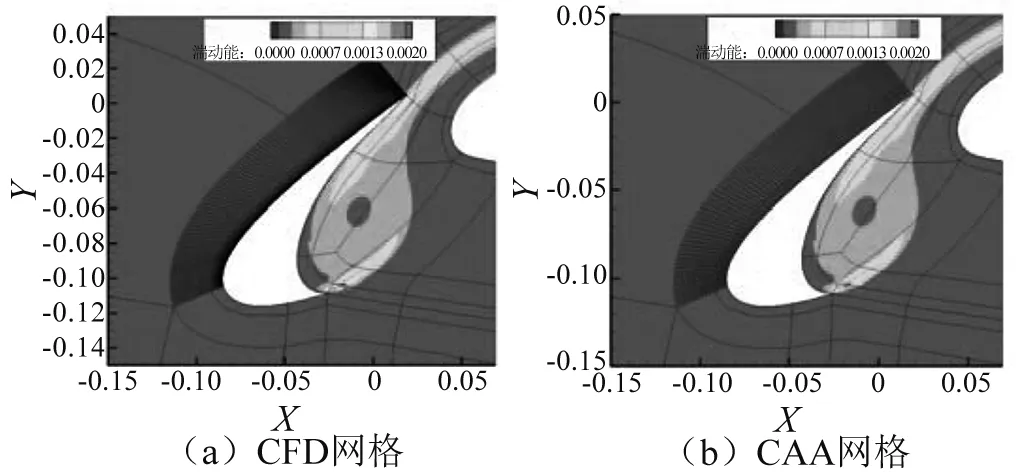
图4 前缘缝翼处的湍动能分布(无量纲)Fig.4 Turbulent kinetic energy of slat

图5为某一时刻SNGR方法计算所得的声传播云图。从图中可以看出：缝翼上下表面的声波在缝翼前缘处相互作用、相互抵消；在襟翼附近，由主翼与襟翼衍生出来的声波、缝翼传递过来的声波、襟翼后缘衍生出来的声波，三者相互作用，出现了明显的干涉现象。

为了定量分析SNGR方法预测缝翼噪声的可靠性，文中开展了监测点的声功率频谱对比和指向性对比。图6给出了监测点分布示意图，以缝翼后缘点为圆心，1.5倍的翼型长度为半径，等角度分布了180个监测点。图7给出了θ=290°,r=1.5位置监测点的声压级频谱图，图7(a)是为采用SNGR方法计算的结果，图7(b)中的两条实线分别代表DLR基于结构网格开发的PIANO声场求解程序和基于非结构网格开发的DISCO声场求解程序的计算结果。将图7(a)、图7(b)进行比较，在大约2 000～10 000 Hz的频率范围内，本文SNGR方法预测的声功率要高于参考文献结果。从整个频率范围来看，计算结果与参考文献结果趋势基本一致。

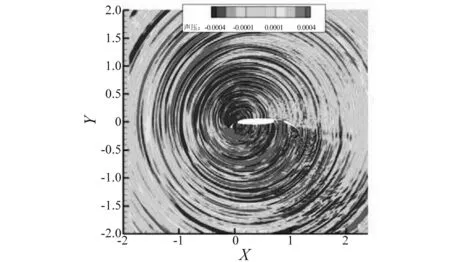
图5 某时刻的声压云图Fig.5 Distribution of sound pressure at sometime

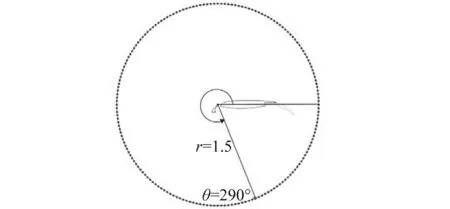
图6 监测点分布示意图Fig.6 Distribution of monitoring points

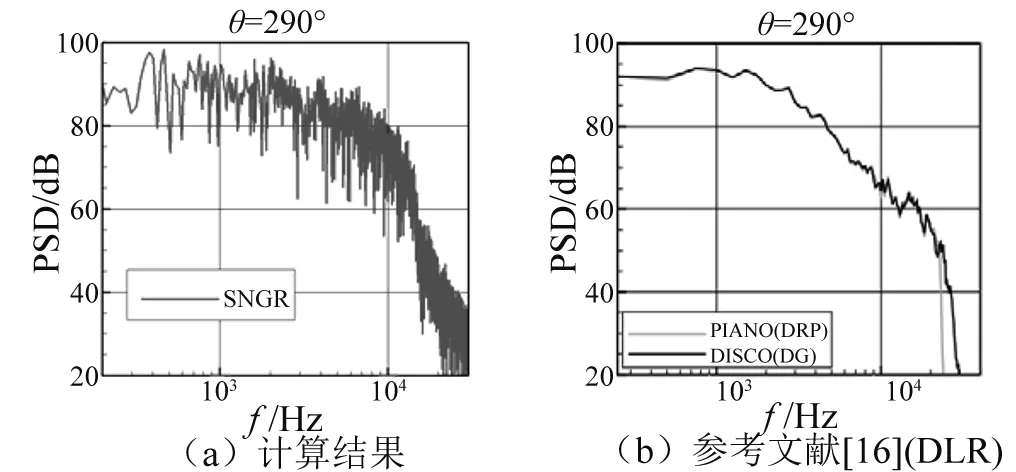
图7 θ=290°, r=1.5处声功率频谱图Fig.7 Sound power spectrum at θ=290°, r=1.5

图8给出了总声压级指向性图，图8(a)为采用SNGR方法计算出的结果，图8(b)中的浅色实线和深色实线分别代表PIANO和DISCO声场求解代码的计算结果。图中可以看出：无论本文计算结果还是参考文献计算结果，总声压级指向性呈现出偶极子特性，总声压级最小点的连线与水平线的夹角在30°左右，与缝翼的偏角基本一致。另外从图中也可看出，不同方法在总声压级量级上基本相当，但在细节分布上有所区别。

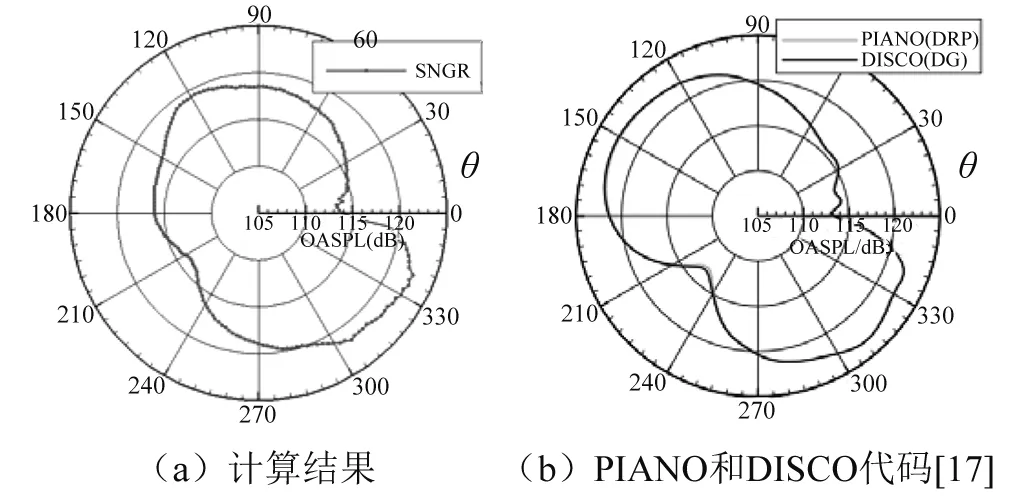
图8 总声压级指向性图Fig.8 Direction of total SPL

从上述研究分析中可以得出以下结论：对于30P30N缝翼宽频气动噪声的计算，本文所搭建的SNGR方法能真实反映出声波间的相互作用，有效给出监测点的声功率频谱，并且指出噪声的指向性分布。这为后文中的增升装置缝翼气动噪声的流动控制措施研究提供技术手段。

3 不同缝翼几何形状对缝翼噪声抑制效果

本节通过改变不同缝翼几何形状来研究分析其对缝翼噪声的抑制效果。计算模型采用了30P30N三段翼模型，计算状态为：马赫数Ma=0.17，迎角Alpha=4，单位尺度雷诺数Re=3.72E+006，参考长度L=0.457，声场计算采用全场统一无量纲时间步长0.000 1。图9为基准构型的计算网格拓扑划分图，该基准构型的CFD网格及CAA网格采用的是第二节中的网格分布。所有构型的网格拓扑和网格点分布均是基于该套网格拓扑进行调整，除缝翼几何形状变化处网格分布有所区别，其余位置网格均保持一致。

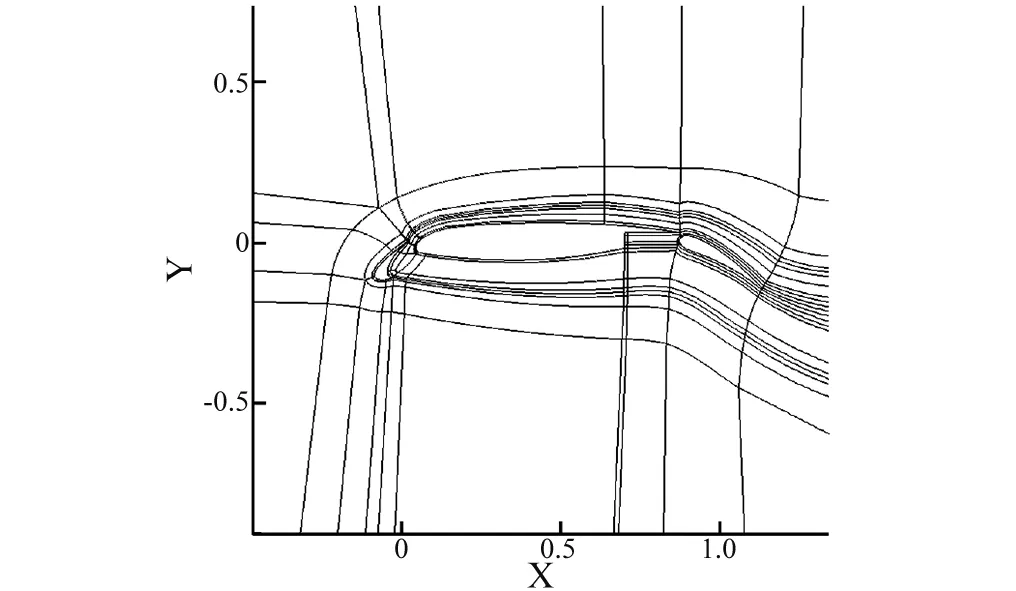
图9 基准构型的网格拓扑划分Fig.9 Mesh topology of benchmark configuration

从30P30N缝翼发声机理可知：通过某种手段增强缝翼前缘处剪切层稳定性，可以降低分离涡与缝翼背风区碰撞的强度，从而达到抑制缝翼噪声的效果。基于这样的思想，本节对缝翼几何形状进行了几种改进设计，如图10所示，分别命名为CASE1、CASE2、CASE3、CASE4。

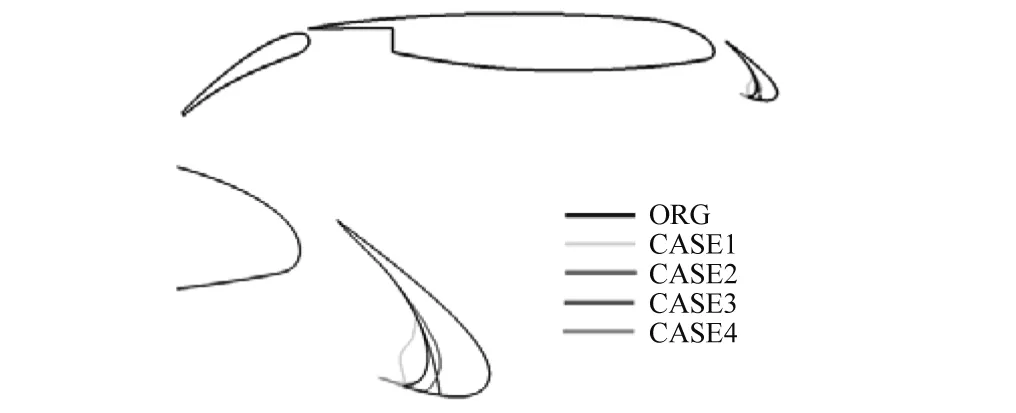
图10 不同几何形状的缝翼示意图Fig.10 Geometry of different slat

图11分别为不同时刻各构型的声传播云图。图12为采用SNGR方法计算出的噪声指向性图，观测点的位置分布可如图6所示。由图11、12中可以均明确的看出：CASE4构型相对于ORG构型，其噪声更小。

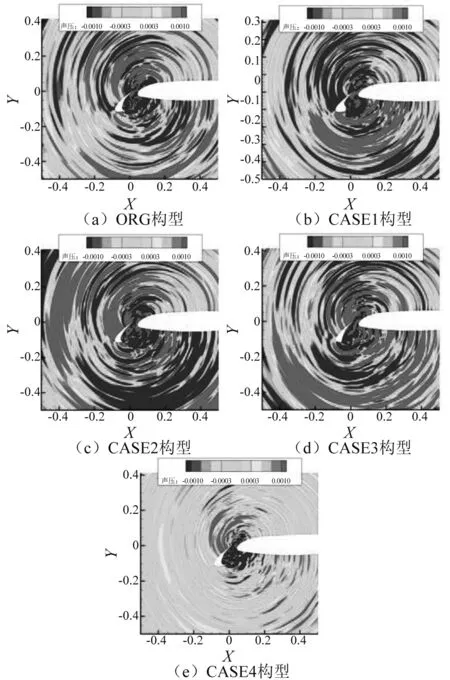
图11 声压分布云图(nt=5 000)Fig.11 Distribution of sound pressure

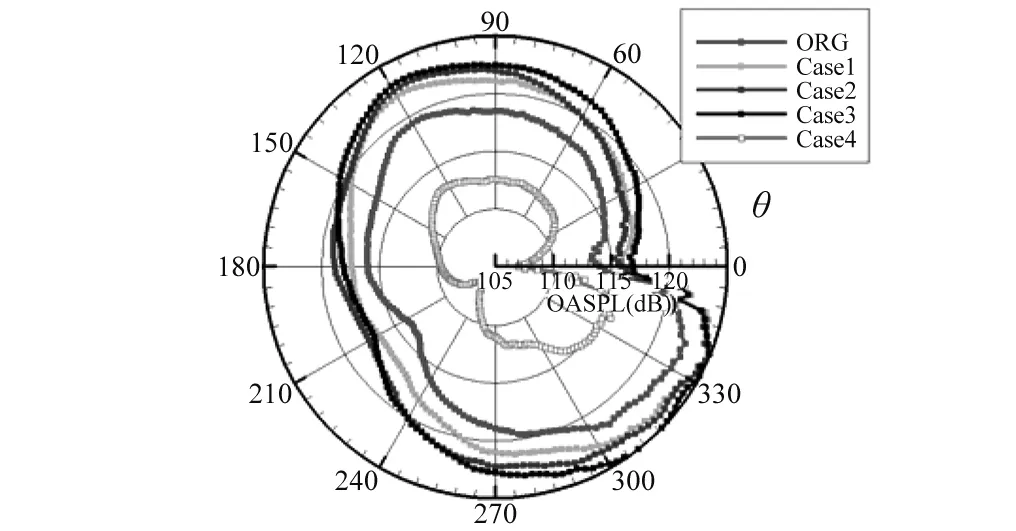
图12 噪声指向性云图Fig.12 Direction of total SPL

为了能可靠解释上述计算结果的可信度以及CASE4构型噪声小的原因，采用Fluent软件中大涡模拟(LES)模型进行求解分析。当非定常残差收敛稳定后，为了有效的对比分析各构型的流场特征，计算分析了各构型的时均流场。定义x，y，z方向的速度的时均值uavg、vavg、wavg分别为：

(13)

式中：un、vn、wn分别为第n步瞬时时刻速度分量。

图13为各构型的马赫数云图，从图中白色圆圈的马赫数分布形态可以看出：CASE4构型的剪切层相对于ORG构型流速更高，更趋于稳定。而CASE1、CASE2、CASE3构型剪切层均易发生分离。图14为各构型的压力云图及流线图，图中白色圈的地方表示分离流与缝翼壁面碰撞区域。从图中可以看出：在这几种缝翼构型中，只有Case4构型碰撞区域的压力相对于ORG构型要小。结合图13、14，分析造成这一结论的原因可能是：Case4构型通过延长缝翼前缘“弯钩”形状，有效增强了剪切层的稳定性，延迟和减弱其分离，以致碰撞区域强度降低。

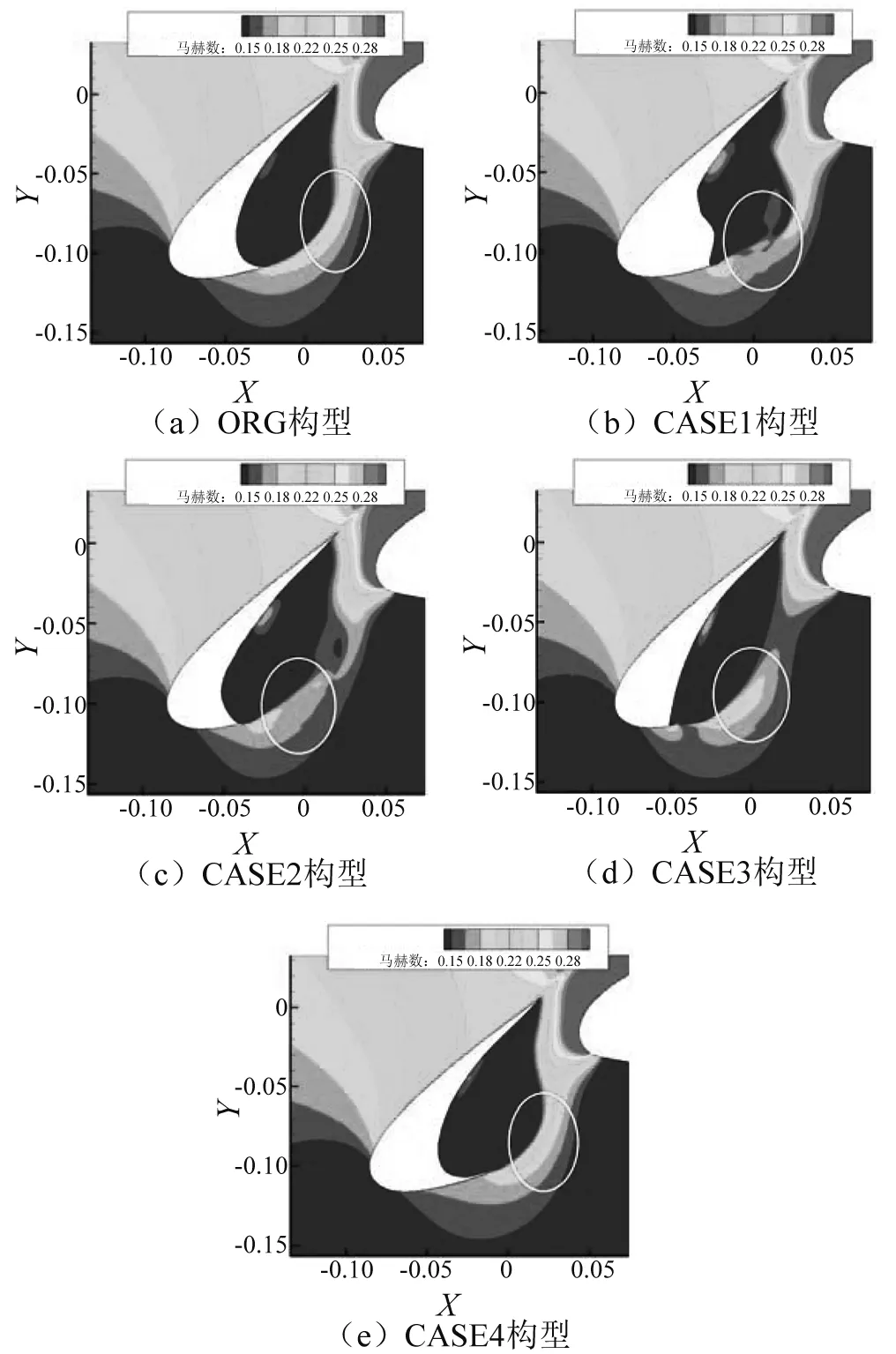
图13 时均马赫数云图Fig.13 Contours of average Mach number

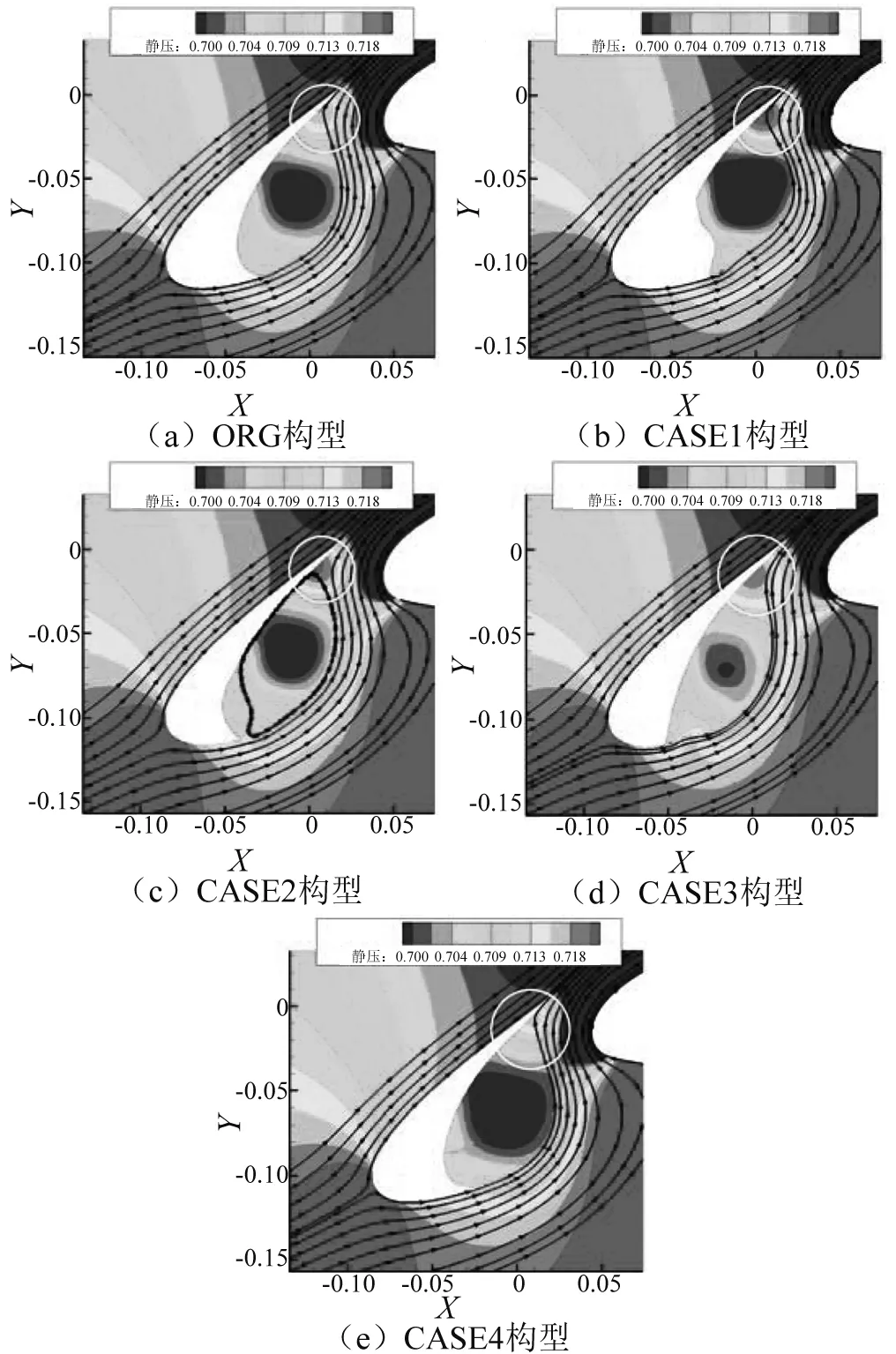
图14 时均压力云图及流线图Fig.14 Contours of average pressure and streamline

为了更进一步说明上述Case4构型减噪效果的可靠性，通过采用可渗透积分面的FWH方程分别对比了各构型在以缝翼后缘点为圆心，50 m为半径，进行了远场监测点的噪声指向性分析。图15为监测点的噪声指向性图。从图中同样可以看出：Case4构型在远场处其噪声强度也要小于ORG构型，这从侧面反映了文中计算方法的正确性及缝翼几何形状改进对噪声抑制效果的有效性。

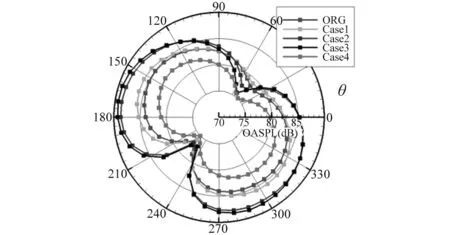
图15 噪声指向性图(FWH)Fig.15 Direction of total SPL (FWH)

4 结 论

本文通过数值模拟，以未加修形的缝翼构型为基准，比较了不同几何形状缝翼构型的噪声抑制效果，得到以下结论：

(1) 通过对比分析30P30N标模的缝翼噪声计算结果与国外学者的计算结果，可以看出：本文所采SNGR噪声预测方法，能有效反映缝翼的噪声分布特点及强度。

(2) 文中所采用的缝翼几何修形措施能有效降低缝翼的气动噪声，其中Case4的减噪效果最佳。

(3) 缝翼的降噪效果与缝翼处剪切层的稳定性有着直接的关系。剪切层的稳定性能有效控制分离涡的发展，减少与缝翼背风区后壁碰撞的激烈程度。

综合考虑了缝翼几何形状对缝翼前缘剪切层稳定性和缝翼背风区的碰撞强度可以发现，文中通过延长缝翼前缘“弯钩”的措施能有效降低缝翼的气动噪声。

参 考 文 献

[ 1 ] EWERT R, DIERKE J. CAA-RPM prediction and validation of slat setting influence on broadband high-lift noise generation[C]. AIAA-2010-3833.

[ 2 ] FOSSO POUANGUE A, MNASRI C. Parameterization and optimization of broadband noise for high-lift devices[C]. AIAA-2013-2065.

[ 3 ] GRUNDESTAM O, PENG S H. Local flow properties in relation to noise generation for low-noise high-lift configurations[C]. AIAA-2012-0278.

[ 4 ] WANG Xin, HU Zhiwei. Detached eddy simulation of high-lift wing slat track and cut-out noise[C]. AIAA-2016-0258.

[ 5 ] MOLIN N. Prediction of aircraft high-lift device noise using dedicate danalytical model[C]. AIAA-2003-3255.

[ 6 ] GUO Y P, YAMAMOTO K J. Component-based empirical model for high-lift system noise prediction[J]. Journal of Aircraft , 2003, 40(5): 914-922.

[ 7 ] REICHE N, LUMMER M. Towards high-lift noise from Fast Multipole BEM with anisotropic synthetic turbulence sources[C]. AIAA-2015-2672.

[ 8 ] STREET C L. Aerodynamic noise reduction for high-lift devices on a swept wing model[C]. AIAA-2006-212.

[ 9 ] YOKOKAWA Y. Noise generation characteristics of a high-lift swept and tapered wing model[C]. AIAA-2013-2062.

[10] MURAYAMA M, YOKOKAWA Y. Study on noise generation from slat tracks using a high-lift wing model[C]. AIAA-2015-3141.

[11] 吕宏强，朱国祥，宋江勇. 线化欧拉方程的高阶间断有限元数值解法研究[J]. 力学学报, 2011, 43(3): 621-624.

LÜ Hongqiang, ZHU Guoxiang, SONG Jiangyong. High-order discontinuous galerkin solution of linearized Euler equations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011,43(3): 621-624.

[12] 卢清华, 陈宝. 基于LES方法的增升装置气动噪声特性分析[J]. 空气动力学学报, 2016, 34(4):448-455.

LU Qinghua, CHEN Bao. Analysis of aeroacoustics characteristics of high lift device using LES method[J]. Acta Aerodynamica Sinica, 2016, 34(4): 448-455.

[13] 乔渭阳, Ulf Michel. 襟翼侧缘噪声的理论模拟与分析[J]. 声学学报, 2002, 27(3): 267-272.

QIAO Weiyang, Ulf Michel. Theoretical study on flap side-edge noise[J]. Acta Acustica, 2002, 27(3): 267-272.

[14] KARWEIT M, BELANC-BENON P, JUVE D, et al. Simulation of the propagation of an acoustic wave through a turbulent velocity field: A study of phase variance[J]. Journal of Acoustic Society of America, 1991, 89(1): 52-62.

[15] BAILLY C, LAFON P, CANDEL S. Astochastic approach to compute noise generation and radiation of free turbulent flows[C]. AIAA-95-029.

[16] CHOUDHARI M, LOCKARD D P. Assessment of slat noise predictions for 30P30N high-lift configuration from BANC-Ⅲ workshop[C]. AIAA-2015-2844.

[17] 徐航手，季振林，康钟绪. 抗性消声器传递损失预测的三维时域计算方法[J]. 振动与冲击，2010, 29(4): 107-110.

XU Hangshou, JI Zhenlin, KANG Zhongxu. Three-dimensional time-domain computational approach for predicting transmission loss of reactive silencers [J]. Journal of Vibration and Shock, 2010, 29(4): 107-110.

[18] 刘俊，杨党国，王显圣. 基于URANS与DDES方法的空腔近场噪声数值研究[J]. 振动与冲击，2016,35(20): 154-159.

LIU Jun, YANG Dangguo, WANG Xiansheng. Numerical simulation of near-field cavity noise by URANS and DDES [J]. Journal of Vibration and Shock, 2016, 35(20): 154-159.