一种新的声发射信号消噪及故障诊断方法

张 瑞， 邓艾东， 司晓东， 刘东瀛， 李 晶

(1. 东南大学 火电机组振动国家工程研究中心，南京 210096； 2. 东南大学 能源与环境学院，南京 210096； 3. 东南大学 信息科学与工程学院，南京 210096)

声发射技术以其响应频带宽、灵敏度高等特点成为近年来旋转机械故障诊断中的研究热点。但是声发射信号易受环境噪声的干扰，尤其是旋转机械运行中产生的大量干扰噪声，使有用的声发射故障特征变得模糊甚至被淹没，从而难以对故障进行有效的分析和诊断。因此，对声发射信号进行降噪处理是实现有效故障诊断的前提。

信号降噪处理的基本方法是滤波，其降噪结果同时也展宽了信号的波形，并对声发射信号中的瞬变成分进行了平滑处理，可能使原始信号损失一些重要的信息，影响信号的本质，并且传统的滤波器消噪方法主要针对平稳信号，而对于非线性、非平稳的声发射信号消噪效果不佳。声发射信号有频响范围宽的特性，而随机噪声的频带通常也比较宽，信号和噪声的频带相互混叠，当信号的先验信息很少的情况下，传统的滤波消噪效果就不太理想。国内外学者已经对声发射信号的消噪进行了诸多有效的研究，并取得了一定的成果。有的学者提出了小波分析和数学处理方法[1-4]。向东阳等[5]采用小波硬阈值函数和软阈值函数进行降噪处理。Tang和Zheng等[6-7]分别利用Morlet小波变换和基于连续小波变换方法对风电设备齿轮箱振动信号和滚动轴承振动信号进行降噪，都取得了不错的消噪效果。但是，小波降噪存在基函数选择、平稳性假设和参数敏感等问题。胡爱军等[8]构建了一种基于数学形态滤波器实现旋转机械振动信号降噪处理方法，可以有效剔除脉冲噪声，对于强噪声干扰的，还需结合傅里叶变换。

傅里叶变换在对信号进行分解的同时也将噪声进行分解，因而存在抑制噪声和保护信号边缘的矛盾，对于准确识别去除噪声有一定的障碍。常用的时频分析方法主要有短时傅里叶变换、Winger-Ville分布、 小波变换和经验模态分解等。但是这几种方法中，又存在缺陷：在短时傅里叶变换中窗函数一旦选定了，它的时频分辨率就固定了[9]，这不符合高频信号分辨率应比低频信号分辨率高的实际要求。Winger-Ville分布虽有很高的时频分辨率，但是对于多分量信号，由于交叉项干扰的存在，其应用受到了很大的限制[10]。小波变换具有多分辨率的特性，但是在应用中需要人为的选择小波基，因此缺乏自适应性,并且不能很好的解决低频干扰的问题。Huang等[11]提出了经验模态分解EMD，该方法对非平稳信号能够进行自适应分解，但是，该方法仍存在一定的缺陷，比如它是一种经验性的方法，仍缺乏完备的理论基础，分解后所得到的模态分量的正交性仍有待论证；其通过包络线进行分解的结束判断标准没有科学性，可能会导致分解的信号出现模态混叠的问题；需要经过多次迭代才可得到完全的IMF分量，耗时长，计算量大[12-14]。法国学者Gilles[15]结合经验模式分解的自适应性和小波分析理论提出经验小波变换EWT。其核心思想是对信号的傅里叶谱进行自适应划分，并建立一组合适的小波滤波器提取不同的AM-FM成分，并对得到的成分作Hilbert变换，获得瞬时频率和幅值。其自适应模态分解数优于EMD，计算量远小于EMD方法并且理论充分。本文将EWT引入到旋转机械声发射故障诊断中，提出了一种基于EWT的消噪和故障诊断的方法，通过仿真实验验证了该方法的有效性。

1 经验小波变换(EWT)

EMD分解方法实质是将原信号f(t)分解为N个IMF分量ci(t)和残差之和，即

(1)

此方法存在筛分迭代终止条件、端点效应和模态混叠等问题。而经验小波变换则是将原信号f(t)分解成N+1个模态函数fi(t)之和，即

(2)

式(2)中的fi(t)定义为调幅-调频信号(AM-FM)，fi(t)的表示如下

fi(t)=Fi(k)cos(φi(t))

(3)

(4)

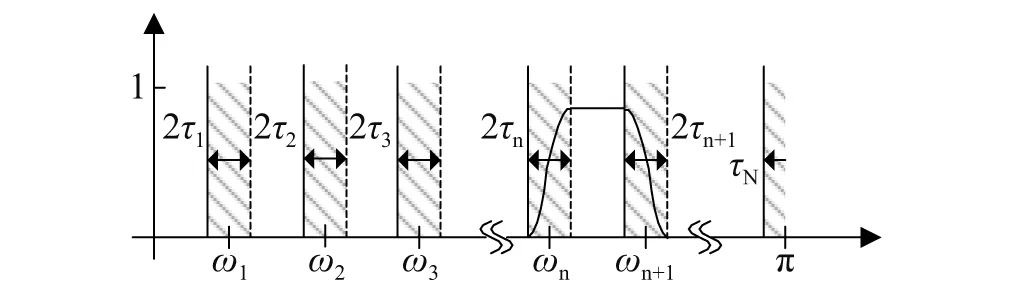
图1 傅里叶轴分割Fig.1 Partitioning of the Fourier axis

(5)

(6)

式(5)和(6)中的τn和β(x)可表示为：

(7)

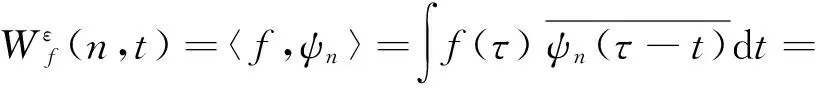
(8)

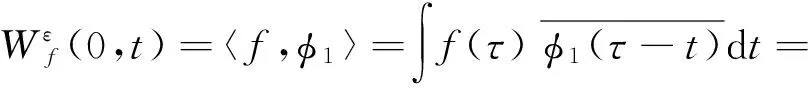
(9)

(10)

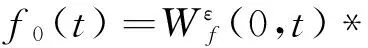
(11)

(12)

2 仿真信号消噪分析

为了验证所提出的基于EWT消噪方法的有效性，用仿真信号加高斯白噪声(噪声强度根据信号本身的强度而定)并消噪处理分析。仿真信号表达式为：

(13)

取1 024个采样点数作为信号长度进行分析验证，如图2所示。含噪仿真信号经EWT分解后的多分辨信号分量如图3(a)，带有噪声的仿真信号一共被分解为6阶固有模态分量。从中可以看出，含噪仿真信号分解后得到的各个经验模态函数fi(t)分量都存在噪声分量。但是噪声大部分呈现在高频率分量中。含噪仿真信号经EMD分解得到8 阶本征模态函数和1 阶残差，如图3(b)所示。

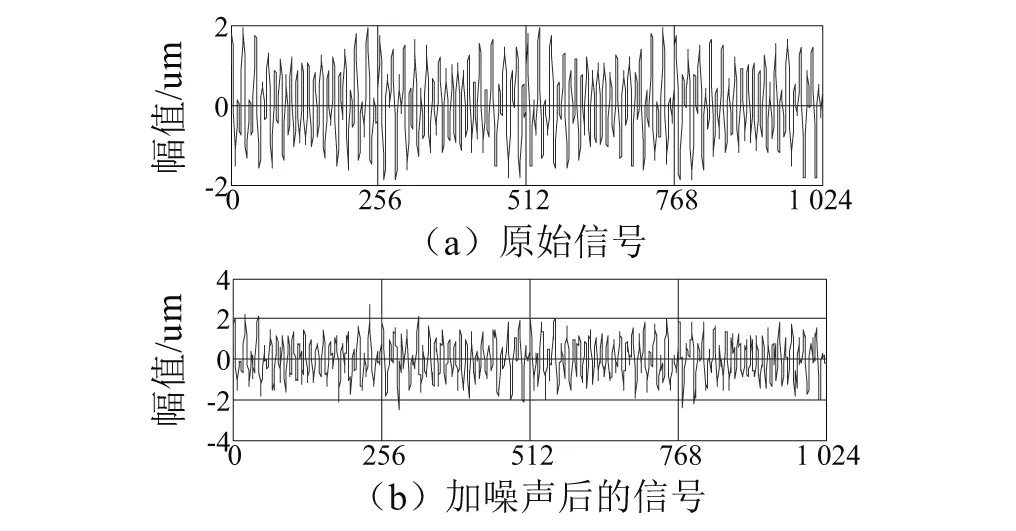
图2 仿真信号和加噪信号Fig.2 Simulation signal and noisy signal

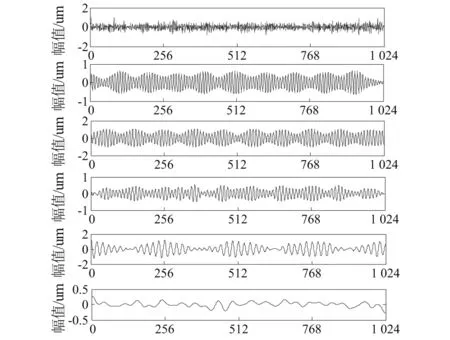
(a) 带噪声信号EWT分解

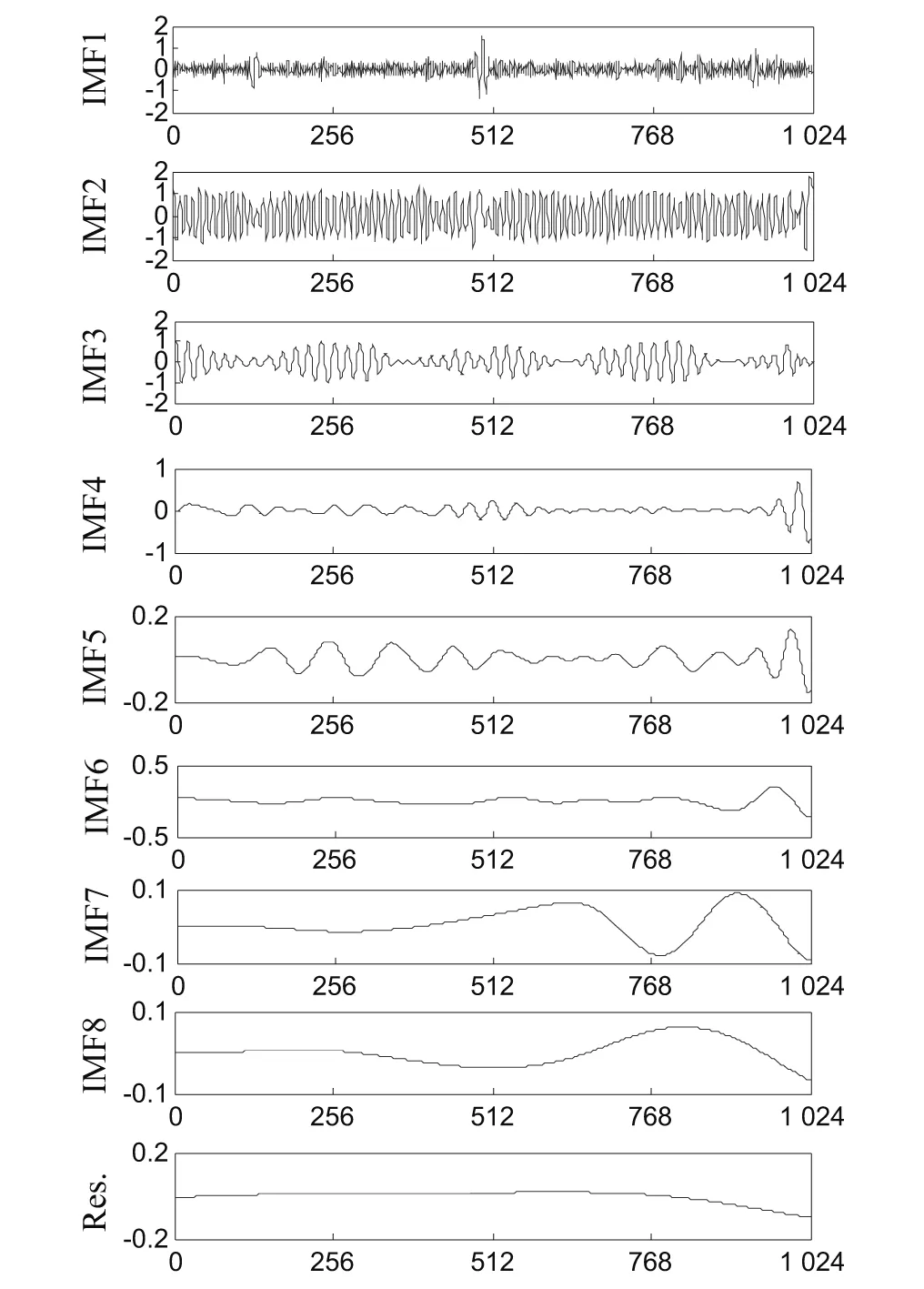
(b) 带噪声信号EMD分解图3 带噪声信号EWT和EMD分解Fig.3 EWT and EMD Decomposition of the noisy signal

从图3中可以看出，噪声大都呈现在高频率模态分量中。EWT和EMD是自适应的分解，能真实地反映信号的分解物理构成，具有不失原信号能量，但是它们分解的层数不一样，EWT自适应模态分解数优于EMD，计算量远小于EMD方法，并且具有较强的鲁棒性。

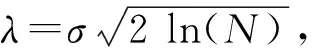
默认阈值消噪，是利用函数生成信号的默认阈值，然后利用函数进行消噪处理，结果如图4(a)所示。全阈值消噪是经由输入信号每层的细节系数的标准偏差估计σ，然后根据σ来调整每层的阈值并进行消噪处理，结果如图4(b)所示。对高频系数进行阈值处理进行消噪是将信号进行小波分解后，利用尺度向量和阈值向量对高频系数进行阈值处理，然后进行重构消噪，结果如图4(c)所示。图4(d)和图4(e)分别为含噪信号基于EWT和EMD消噪后的信号。

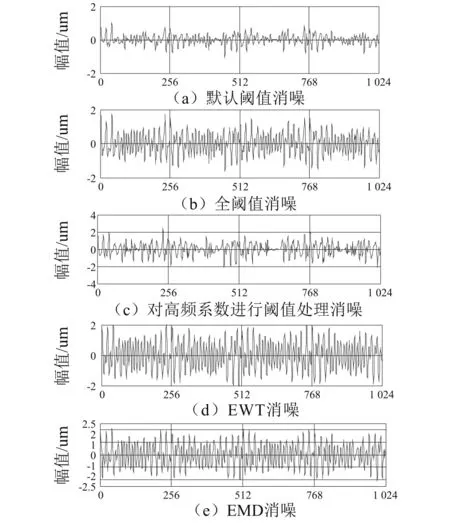
图4 信号消噪后波形Fig.4 The chart of signal after de-noising

从图4(a)中可以看出，含噪信号经过默认阈值消噪后失真比较严重；图4(b)所示全阈值消噪比默认阈值消噪效果好一些，但波形也发生失真；从图4(c)中可以看出，经高频系数阈值处理后进行消噪，其幅值超过原始信号的幅值，显然消噪效果不理想，且波形失真严重；图4(e)中，经EMD消噪后的信号也存在幅值超过原始信号，说明还存在显在的噪声；图4(d)中可看出，含噪仿真信号经EWT小波消噪后最接近原波形，效果显著。为了能定量的评价五种消噪效果，采用输出信号的信噪比(SNR)和均方根误差(RMSE)作为评价指标，结果如表1所示。

从表1可以看出，EWT消噪信噪比最大，均方根误差值最小，其消噪效果最优。

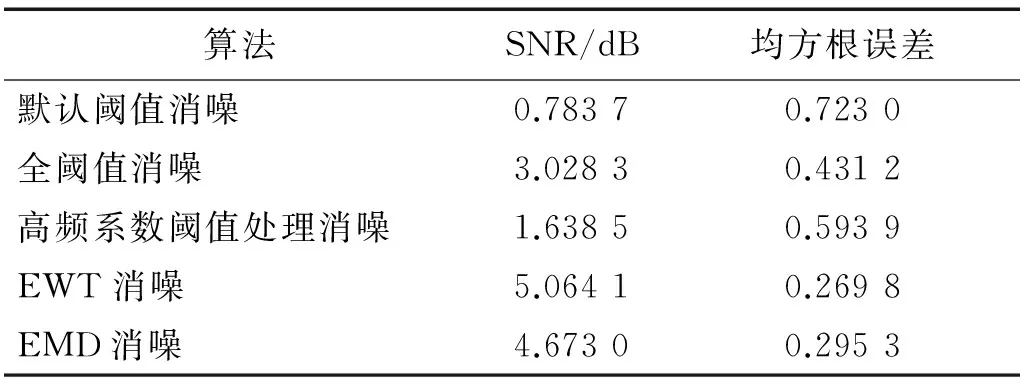
表1 五种方法仿真信号消噪结果比较

3 碰摩声发射信号消噪分析

3.1 碰摩声发射信号实验系统

本文碰摩声发射实验系统由转子碰摩实验台、传感器、前置放大器、调速器和声发射采集系统组成，如图6所示。图5为碰摩实验系统模拟图，转子碰摩试验台为柔性转子试验台，由三个具有滑动轴承的轴承座用于支撑转子，两个碰摩圆盘，碰摩螺钉组成。碰摩螺钉可以通过盖状导波板上螺孔指向转轴中心，并与碰摩圆盘侧面相接触。当转子以一定转速旋转时，调节碰摩螺钉与碰摩圆盘发生碰摩，产生的碰摩AE信号经由导波板被声发射传感器所接收，传播路径为碰摩点-碰摩螺钉-导波板-传感器，传感器接近AE源，只经过碰摩螺钉-导波板一次表面传递，故可将该位置传感器的波形看作近似的AE源[17]。通过调节碰摩螺钉旋入深度来模拟不同强度的碰摩。调速器实现电机0～10 000 r/min范围的无极调速；为了降低由于介质不连续而引起的声发射波形畸变，在接触面之间填充耦合剂。

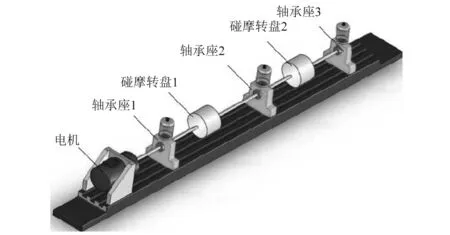
图5 碰摩实验系统模拟图Fig.5 Rub-impact experimental system simulation diagram

图6 实验系统Fig.6 Experimental system

3.2 实验结果与分析

在本实验中采用UT-1000传感器，AE信号由内置PCI-2声发射采集卡的工控机采集，设置AE信号采样频率为1MbPS，采样点为20 000，滤波频带设置为0～200 kHz,放大增益为40 dB。碰摩信号如图7(a)所示。7(b)则为添加SNR=-5 dB高斯白噪声后波形图。

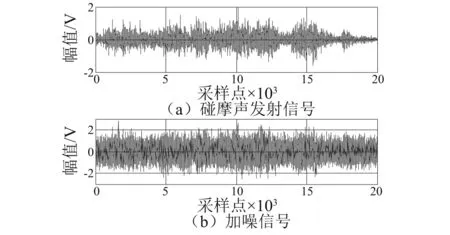
图7 碰摩声发射信号及加噪后的波形Fig.7 Rub-impact AE signal ahd noisy signal

对含噪碰摩声发射信号分别用以上五种方法进行消噪处理，其结果如图8所示。图8中(a)～(e)分别为经过全阈值消噪、默认阈值消噪、对高频系数阈值处理消噪、EWT消噪和EMD消噪后的波形图。从图中可以清晰的看出消噪效果。图8(a)和图8(b)的波形与声发射信号相比有明显的失真，其幅值范围降到[-1,1]之内。图8(c)和8(e)同图7(b)相比已去除一部分噪声，但同图7(a)相比，仍可看出含有大量的噪声成分，有效碰摩信号被噪声所湮没。图8(d)为本文中提出的基于EWT消噪方法，可以看出其波形与图7(a)波形十分相似，其消噪性能明显优于其他方法。定量评价各消噪方法的结果如表2所示。显然，EWT消噪信噪比最大，均方根误差值最小，其消噪性能最优。

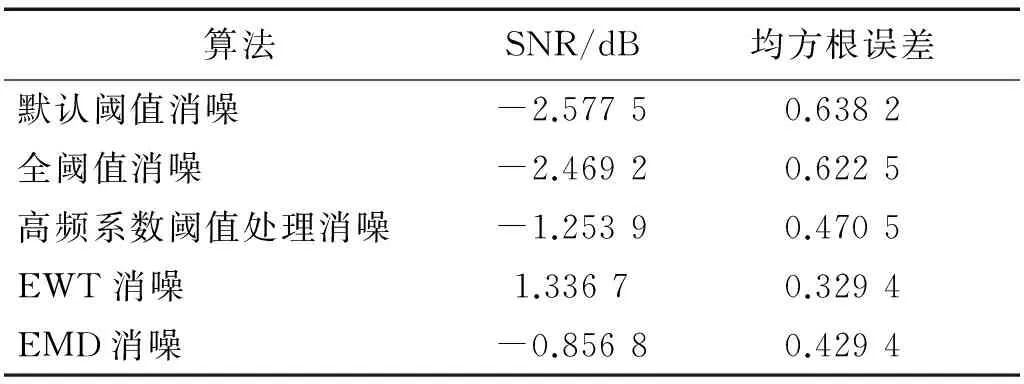
表2 五种方法实验信号消噪结果比较

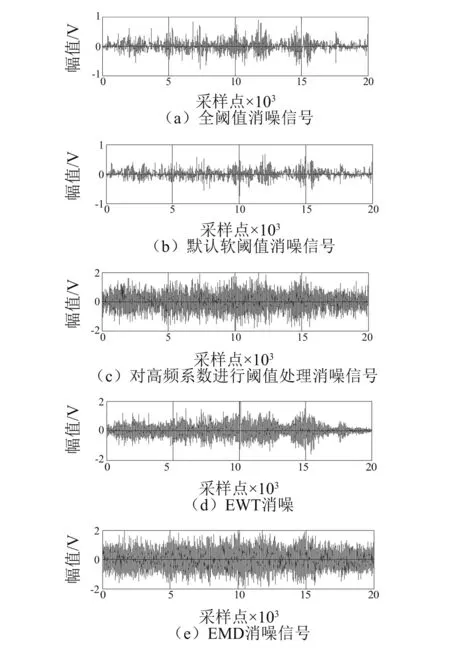
图8 含噪实验信号消噪后波形图Fig.8 The de-noised signal chart of noisy experimental signal

4 基于EWT方法的故障诊断识别

基于EWT在自适应频率分解上的优势，将其应用到旋转机械声发射故障诊断中，为了验证其有效性，并将其与以上分析中消噪效果相对来说较好的EMD方法进行比较。在试验台上分别在无碰摩状态下和有碰摩状态下测得实验数据。其波形图如图9所示。

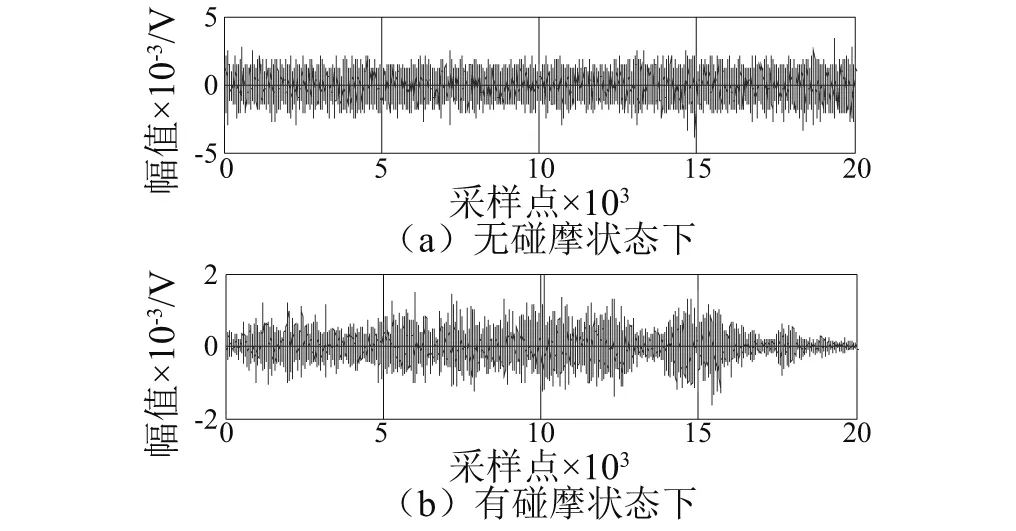
图9 两种状态下碰摩AE信号波形图Fig.9 Rub-impact AE signal chart under two conditions

分别用EWT和EMD方法对有碰摩状态下的声发射实验数据进行分解。EWT分解出来的分量与EMD分解出来的固有模态分量如图10所示。

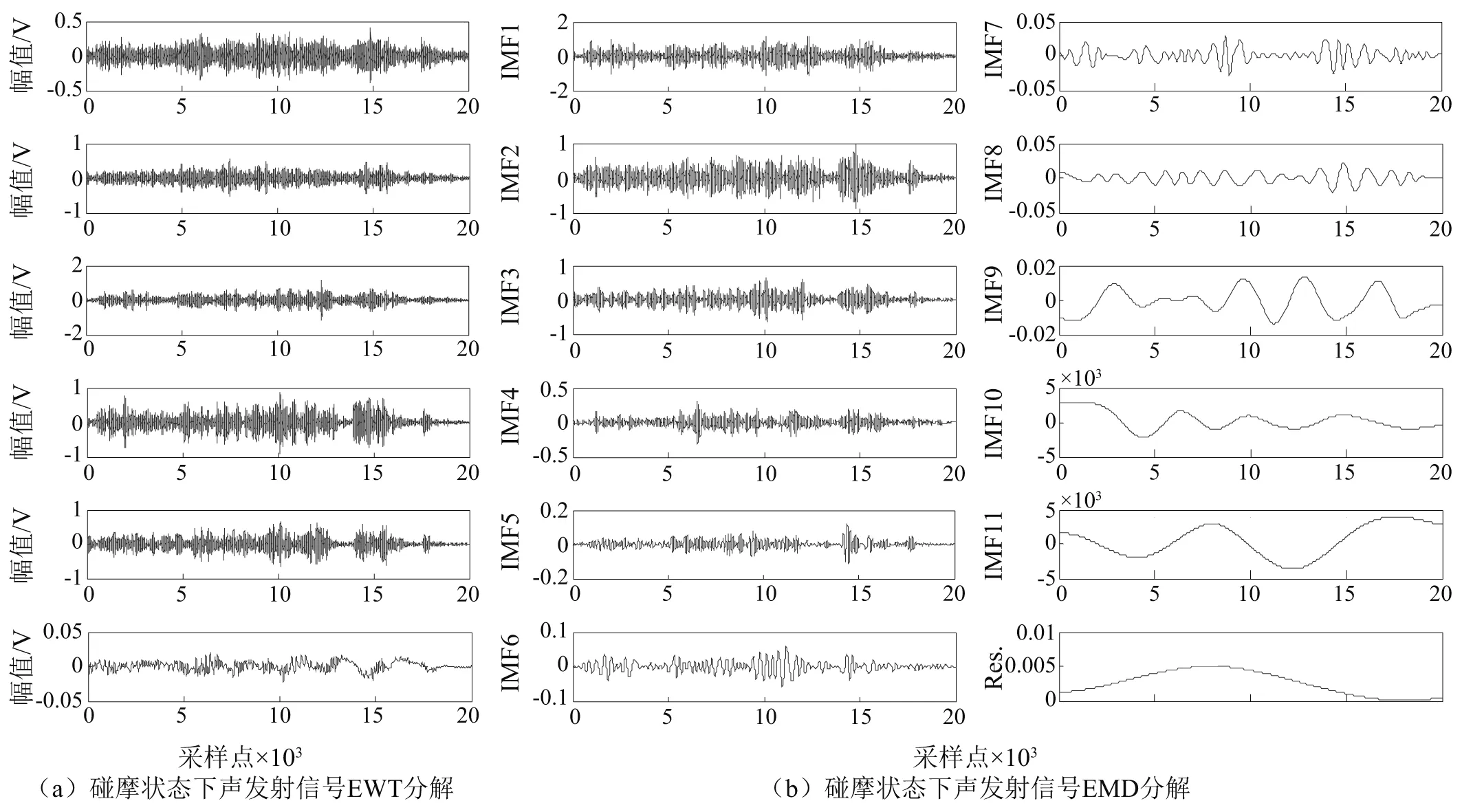
图10 有碰摩声发射信号的EWT和EMD分解Fig.10 EWT and EMD decomposition of heavy rub-impact AE signal

由图10中可以看出，相对于EWT变换，信号经EMD分解出了过多的虚假模态。对不同碰摩状态声发射信号经EWT和EMD分解后的所有分量进行希尔伯特变换并且进行组合，得到被分析信号的全部时频信息。如图11所示。

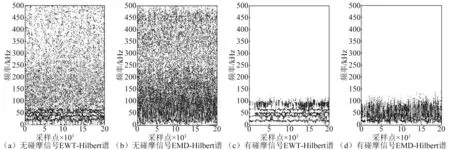
图11 实验信号的EWT-Hilbert谱和EMD-Hilbert谱Fig.11 EWT-Hilbert and EMD-Hilbert spectrum of the experimental signal

图11(a)和(b)分别为无碰摩信号经过EWT和EMD变换后的Hilbert谱，从图中可看出无碰摩状态下声发射信号的频率主要分布在500 kHz之内，频点分布杂乱无规律，符合无碰摩状态下声发射的频率分布特征；对比两种变换方法后的Hilbert谱，EWT-Hilbert谱的频率的得到了很好的自适应划分，可以看出频率带之间几乎没有重叠，而EMD-Hilbert谱中的频率带都重叠到一起。图11(c)和图11(d)为有碰摩声发射信号的EWT-Hilbert谱和EMD-Hilbert谱，从图中可以看出有碰摩状态下声发射信号同无碰摩状态下频带特征一样，但其能量主要集中在100 kHz以内。对比图11(a)和图11(c)，图11(b)和图11(d)可看出两种方法都可通过不同状态下能量的频带分布来判断碰摩的发生，而EWT变换可以按照频率的特征从低频到高频对信号进行有效的自适应分解，从一定程度长克服了EMD分解存在的模态混叠及分解出虚假分量的问题，且运算量大大小于EMD，因此其使用效果优于EMD。

5 结 论

本文介绍了经验小波变换(EWT)理论及特性，提出了基于EWT的信号消噪方法和碰摩故障识别方法，并通过仿真和碰摩声发射实验验证了该方法的有效性，得出以下结论。

(1) EWT本质是基于频率自适应划分的一种变换，可以有效地分解出信号的固有模态，分解出的模态少，不存在虚假模态。

(2) 基于EWT的消噪方法可以有效去除噪声，其性能优于基于小波基dB4和EMD的消噪方法。

(3) 采用EWT方法可以有效识别碰摩故障的发生，为碰摩故障的诊断提供了一条新的途径。

[ 1 ] WATSON S J, XIANG B J, YANG W X, et al. Condition monitoring of the power output of wind turbine generators using wavelets [J]. IEEE Transactions on Energy Conversion, 2010, 25(3): 715-721.

[ 2 ] 孟宗, 李姗姗. 基于小波改进阈值去噪和HHT的滚动轴承故障诊断[J]. 振动与冲击, 2013, 32(14): 204-214.

MENG Zong, LI Shanshan. Rolling bearing fault diagnosis based on improved wavelet threshold de-noising method and HHT [J]. Journal of Vibration and Shock, 2013, 32(14): 204-214.

[ 3 ] CHEN Q X, YE M X. Analysis of the fault diagnosis method for wind turbine generator bearing based on improved wavelet Packet-BP neural network [J]. Communications in Computer and Information Science, 2014, 463: 13-20.

[ 4 ] 许同乐, 郎学政, 张新义, 等.基于EMD相关方法的电动机信号降噪的研究[J]. 船舶力学, 2014, 18(5): 599-603.

XU Tongle, LANG Xuezheng, ZHANG Xinyi, et al. Study on the electric motor vibration signal de-noising using EMD correlation de-noising algorithm [J]. Journal of Ship Mechanics, 2014, 18(5): 599-603.

[ 5 ] 向东阳, 吴正国, 侯新国, 等. 改进的多小波变换系数相关去噪算法 [J]. 高电压技术, 2011, 37(7): 1728-1733.

XIANG Dongyang, WU Zhengguo, HOU Xinguo, et al. Improved de-noising method using the correlation of multiwavelet coeff icient [J]. High Voltage Engineering, 2011, 37(7): 1728-1733.

[ 6 ] TANG B P, LIU W Y, SONG T. Wind turbine fault diagnosis based on morlet wavelet transformation and wigner-ville distribution [J]. Renewable Energy, 2010, 35: 2862-2866.

[ 7 ] ZHENG H, LI Z, CHEN X, et al. Gear fault diagnosis based on continuous wavelet transform [J]. Mechanical Systems and Signal Processing, 2002, 16(2/3): 447-457.

[ 8 ] 胡爱军, 唐贵基, 安连锁. 基于数学形态学的旋转机械振动信号降噪方法[J]. 机械工程学报, 2006, 42(4): 127-130.

HU Aijun, TANG Guiji, AN Liansuo. De-noising technique for vibration signals of rotating machinery based on mathematical morphology filter [J]. Chinese Journal of Mechanical Engineering, 2006, 42(4): 127-130.

[ 9 ] 李国鸿, 李飞行. STFT在航空发动机振动信号处理中的应用[J]. 测控技术, 2013, 32(4): 45-49.

LI Guohong, LI Feixing. Application of STFT in the field of aero-engine vibration signal processing [J]. Measurement & Control Technology, 2013, 32(4): 45-49.

[10] 向玲, 唐贵基, 胡爱军. 旋转机械非平稳振动信号的时频分析比较 [J]. 振动与冲击, 2010, 29(2): 42-45.

XIANG Ling, TANG Guiji, HU Aijun. Vibration signal’s time-frequency analysis and comparison for a rotating machinery [J]. Journal of Vibration and Shock, 2010, 29 (2): 42-45.

[11] HUANG N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [C]. The Royal Society, 1998, 454: 903-995.

[12] 郭淑卿. EMD分解区域的数据研究 [J]. 信号处理, 2010(2): 277-285.

GUO Shuqing. Data discussion of the EMD method in the practice [J]. Signal Processing, 2010(2): 277-285.

[13] 王海梁, 熊华刚, 吴庆, 等. 一种改进的基于EMD分解的超宽带信号消噪算法 [J]. 电讯技术, 2012(4): 461-465.

WANG Hailiang, XIONG Huagang, WU Qing, et al. A novel denoising algorithm for UWB signals based on empirical mode decomposition [J]. Telecommunication Engineering, 2012(4): 461-465.

[14] 滕建方, 王俊, 李维. EMD边缘效应问题的一种处理方法[J]. 教练机, 2014(1): 50-53.

TENG Jianfang, WANG Jun, LI Wei. A disposition method for EMD edge effect problem [J]. Trainer, 2014(1): 461-465.

[15] GILLES J. Empirical wavelet transform [J]. IEEE Transactions on Signals Processing, 2013, 61(16): 3999-4010.

[16] HUANG D, LIU Y. Characteristics of EMD filter bank and identification of abnormal sound of ball bearing [J]. Journal of Vibration Measurement & Diagnosis, 2012, 32(2): 332-336.

[17] 邓艾东, 童航, 张如洋,等. 基于模态分析的转子碰摩声发射特征[J]. 东南大学学报(自然科学版), 2010, 40(6): 1232-1237.

DENG Aidong, TONG Hang, ZHANG Ruyang, et al. Characteristics of rub-impact AE signals in rotating machinery based on modal analysis [J]. Journal of Southeast University (Natural Science Edition), 2010, 40(6): 1232-1237.