学习双机制理论在数学教学中的应用——以“多边形内角和”的教学为例*

孙自海 王道宇

(1.合肥第六十八中学 2.合肥市教育科学研究院 安徽合肥 230001)

数学由概念、定理、公式和法则组成，教学时加以正确阐述，才能实现深度教学之目的。

下面以上海科技出版社出版的教育部审定的义务教育教科书数学八年级下册中的“多边形内角和”的教学为例，对怎样做到准确理解学习双机制理论，从而实施教学作一探讨。

1.准确理解

教师在教学时，参考最多的资料是教师教学用书，而教师教学用书却不是教材编写人员撰写的。因此，教师教学用书的编写人员对课程标准的理解有限，对教材的编写意图理解有限。教学时要准确理解所教内容与学习双机制理论之间的定位。

1.1 课型定位

“多边形内角和”是上海科技出版社出版的教育部审定的义务教育教科书数学八年级下册第19章第1节第1课时的内容，本内容的课型是数学概念和规律教学相结合的课型，在概念教学课型中，本内容的概念形成过程不从属于分类研究、聚类研究、规律研究的形成过程，而规律教学课型中属于推理研究的教学过程结构，采用的流程为

1.2 知识分类

学习双机制理论中把知识分为联结陈述性知识、联结程序性知识、运算陈述性知识和运算程序性知识四类，落实到多边形内角和中，诸如多边形概念，多边形的边、顶点、内角、外角、对角线、凸多边形的概念，多边形内角和定理推理，多边形内角和定理应用的知识分类如下：

1.3 思维建构

多边形，多边形的边、顶点、内角、外角的这种联结陈述性知识可以通过类比三角形获取，而对于对角线、凸多边形的这种联结陈述性知识就只有通过逻辑推理的方法获取。

式中：n为支铰座联结螺栓数量；yi(i=1,2,…,n)为计算螺栓到中和轴的距离，ymax为螺栓到中和轴的最远距离。

多边形内角和的推导属于运算程序性知识，属于规律教学课型，其流程为提出问题、形成猜想、推理探究、归纳结论、运用结论。因此在三角形内角和为180°的基础上，四边形的内角和为多少呢？提出问题，用分割转化的方法，把四边形分割为两个三角形，其内角和为360°=(4-2)×180°，然后对五边形、六边形进行探究，那么n边形的内角和是否为(n-2)×180°？形成猜想，通过逻辑推理的方式得到正确的结论。也即是说运算程序性知识可以通过逻辑推理的方式获取。

多边形内角和的应用我们的理解是联结程序性知识，这种知识我们是通过计算和解方程的方式来获取的。

2.教学实践

教学实践中又如何把为联结陈述性知识、联结程序性知识和运算陈述性知识，运算程序性知识落到实处的呢？现以“多边形内角和”的教学为例，教学时我们采用如下步骤：

2.1 任务问题化

多边形的内角和有关概念隶属于联结陈述性知识，但这种知识可以通过类比和逻辑推理的方式获得，因此，教学中采用任务问题化形式组织教学，设计如下问题：

(1)你能回忆出三角形是怎么定义的吗？三角形中的三条线段有什么限制？

(2)三角形有哪些相关概念？

(3)你能仿照三角形的定义给多边形下定义吗？

(4)你能仿照三角形的相关概念给多边形的相关概念下定义吗？

(5)你能体会出对角线、凸多边形的定义与多边形及多边形的相关概念有什么不同吗？

(6)多边形的表示由哪两种元素组成？

通过对以上问题的诠释，从三角形，三角形的边、顶点、内角、外角类比出多边形，多边形的边、顶点、内角、外角，而对角线和凸多边形的相关概念就只能用逻辑推理的方法获得了。

2.2 推理分步化

多边形的内角和定理隶属于运算程序性知识，其流程为提出问题、形成猜想、推理探究、归纳结论、运用结论。多边形的内角和的推导程序两步：

第一步，获取转化的方式，主要是分割，给学生在思维上铺设台阶。

学生在对四边形进行分割时，一生在探究时首先在四边形的内部取一点，连接各顶点(图1)，得到四个三角形，其内角和为4×180°-360°=360°。但该生的思维不是最简思维。一生根据四边形的四个顶点只有一个是不相邻的知识，于是连接不相邻的两个顶点形成对角线(图2)，这时分割成两个三角形，得其内角和为360°，该生的思维最简。一生过一顶点作不相邻边的平行线(图3)，利用两平行线被第三条直线所截的同旁内角互补和同位角相等的知识，也能得到360°。一生过两顶点向所对边作垂线(图4)，因其中有一矩形，也能得到360°。一生延长两对边，通过三角形的外角和相邻内角的关系，也能得到360°(图5)。但后三位学生的方法不具有一般性，因此应当排除，说明学生的思维比较活跃。一生在形外取一点，连接各顶点，也能得到360°(图6)。一生在其中一边上取一点，分割成三个三角形，也能得到360°(图7)。这七位学生的推导方法中，只有第二位和第七位学生的思维最简洁。

第二步，获取定理的统一性，为今后学习数学归纳法打下基础。

由三角形出发，到四边形时从一个顶点出发如何连接两个顶点，形成多少个三角形，五边形呢？n边形呢？得到下表：

边数引出对角线的条数分成三角形的个数内角和412360°523540°…………nn-3n-2(n-2)×180°

利用三角形的内角和，把未知转化为已知，如图8所示。

2.3 应用具体化

在得到多边形内角和定理的情况下，如何应用这一联结程序性知识呢？我们的做法是应用具体化。

2.3.1 直接应用

(1)求十边形的内角和；

(2)求如图9中x的值.

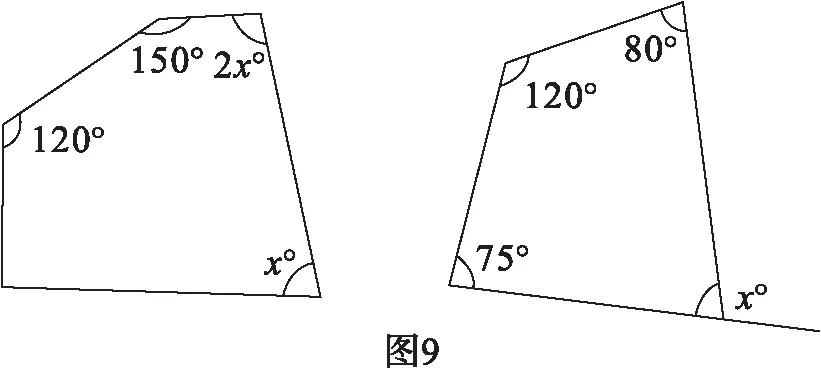
2.3.2 思想应用

①已知一个多边形的内角和为1080°，则它的边数为。

②已知一个多边形的每一个内角都是156°，则它是边形。

2.4 学习小组化

在学习过程中，如何实现任务问题化、推理分布化、应用具体化的呢？我们的做法是把全班学生分成若干小组，每组4-6人，围绕任务问题，推理步骤，具体应用，展开讨论，然后小组派代表交流各自的学习情况，老师纠正学生在学习中的问题。

总之，教师只有按学习双机制理论中的知识分类对所授内容定位，明确所授内容属于哪种课型，说清进行获取知识的途径，让学生积极参与，获得成功体验，这样不仅能使学生获得知识更能让学生形成能力。