以情贻知 以美启真——中考复习摭谈

☉山东省滨州市北镇中学初中部 邢成云

郑毓信教授谈到“语文教学是以情贻知，数学是以知贻情”，数学也不妨适时来点“以知贻情”，尤其是中考复习这个老生常谈的教学话题，复习的内容由于不再新鲜，纵然是“打开书了然，关上书茫然”的低浅状态，但学生面对时那种新课的激情难再，这种情绪势必削弱复习的效果，复习这个老歌委实不好唱.基于这些认识，去年的中考复习，笔者尝试了“以文化人”的行走方式，从外形上把课堂打造成带有文化味的场域，无形中调度了学生复习的积极性，实践证明，效果明显.恰如瑞士心理学家皮亚杰所言：“兴趣是能量的调节者，它的加入便发动了内在储存的力量，足以使工作变得有乐趣.”本文通过一个“特殊三角形”的单元复习教学谈谈笔者的点滴之为，请同仁指正.

一、单元结构化

精致化结构，这是笔者复习教学的举措之一，通过师生的交流活动使得视觉美与内涵美有机结合，立足整体把单元复习的核心线索（有的包括知识技能、思想方法等）勾勒出来，这种结构化、系统化的纲要信号，让人一目了然，于胸生根，无形中调度了学生的复习心向，增进了学生积极的情感体验，同时复习的脉络套路得以渗透，形成了具有迁移性的板块，为后续复习四边形提供了可资借鉴的思路系统.

课时规划：3课时（等腰三角形+等边三角形+直角三角形），单元结构化当属第1课时的前奏.

二、一图一世界——与等腰第二次握手（第1课时）

教学说明：“拟题”是笔者复习教学的又一举措，每天的复习课都有一个别样的标题，力求让学生在进入复习状态前先眼前一亮，既能见证复习的主题，又蕴含着文学的意味，知情兼备，可有效调度学生复习的积极心向.

过程设计如下：

环节1：展图.

图1

（大脑风暴，见图想性）见到图1，同学们能想到哪些相关知识？

从性质、判定两个基本维度展开，并揭示它们的互逆性，形成等腰三角形复习导图（图2）

图2

教学说明：见到图形的大脑风暴，迅速获得关于图形的联想，基于图形的研究角度而呈现，让图式挥尽洪荒之力，久而久之就会形成思考问题的有序化，傅学顺先生称之为：“见微知著，联想快速反应法则.”作为几何部分的复习，一图为基，繁衍生息，简约中蕴大气，变化中见本质.同时这种知识唤醒的序列化、集约化，若再通过图式展示出来，会愈加直观明了，且知识的内在关联蕴含其中，在发散中凝聚成“等腰”板块，形成知识的整体缩影，能有效降低学生的外部认知负荷，便于学生应用时对知识的记忆与调度.这种内在的逻辑美与外在的视觉美的联袂，彰显出感性与理性融汇的光辉，有着浓浓的浪漫韵致.

环节2：在图1中加补条件，使之变成更加特殊的等腰三角形，并研究揭示它们三边之特殊关系.

边特殊：等边三角形，各边关系1∶1∶1.

角特殊：（1）等腰直角三角形（顶角90°），各边关系1∶

教学说明：立足一图，再次赋予特殊性能，使之愈加特殊化，这也是局部之内“一般走向特殊”的进一步印证，通过个性思考、集思广益的交叠活动感知并识得图形学习的基本走向，这已经有了自编自拟的味道，看似漫天索问，其实是在渗透几何图形的研究策略，这种统领性的观念是高位的，弥足珍贵的.另外，这一汇聚的过程中不乏等腰三角形性质与判定、全等与相似性质及判定等的联手，核心的几何知识贯通其中，是以点带面的辐射性复习，实践证明，效果良好.

环节3：盘点等腰三角形的基本图并证明之.

除了上述导图中列出的“角分线+高线、中线+高线、角分线+中线”，还有常见的以下三类：

（1）Rt△+斜边中线（图3中的△ACD与△DBC）.

图3

（2）角分线+平行线（图4中的△EBC，图5中的△OCD，图6中的△ADC，图7中的△ABC）.

图4

图5

图6

图7

（3）双垂直+角分线（图8中的△CEF，图9中的△MBC）.

图8

图9

教学说明：盘点基本图形不是拼盘式堆砌，而是基于三角形三条重要线段之间以及平行线等的不同组合，通过图式的引领作用把相关的基本图统摄起来，形成知识模块，是对核心几何知识的凝聚，本身既是基本图式，又是一道道题目，形成了梳理零散知识、熟悉基本技能、显化基本方法、渗透基本思想、发展整体思维的综合场景.

环节4：返扣基本图的演练.

（1）如图10，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点P，过点P作DE∥BC，分别交AB、AC于点D、E，则图中等腰三角形的个数是（ ）.

A.5个 B.4个 C.3个 D.2个

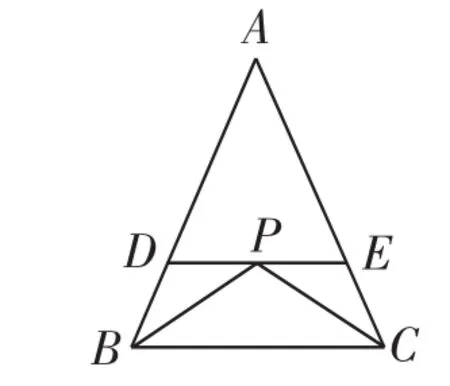
图10

图11

（2）如图11，在△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，E为AC的中点，连接DE，则△CDE的周长为（ ）.

A.20 B.12 C.14 D.13

图12

图13

（4）如图13，在四边形ABCD中，AD∥BC，AE平分∠DAB，BE平分∠ABC，且AE、BE交CD于点E，试猜想AB、AD、BC之间的数量关系并证明.

教学说明：利用几何部分充满基本图的特点，设置相关问题，通过具体题目返扣基本图，彰显基本图的导向之用，便于学生集约知识、积累经验、系统思想，同时砥砺了联想能力、发展了发散思维.其中前三个问题比较简单，从不同的角度展现了等腰三角形基本图式的价值，题目（4）上了一个台阶，有较大的挑战性，方法思路的丰富，集中体现了图式模型的作用，但模型需要构建，可作平行线、可截取等线段、可延长后相交等不拘一格，但同归于与原角平分线联手构造出等腰三角形的模型，充分展现了图式模型的灵活使用，这是一道拓展思维含量高、智能价值高的好题！

环节5：小结与作业.

小结：凝聚图式，提升认识（略）.

作业：（1）重新梳理等腰三角形以及更特殊的等腰三角形等基本图形.

（2）整理课堂上自己未解决好的题目.

三、试看考题哪里来——等边三角形考题面面观（第2课时）

教学说明：这一课时定位于师生共同研究正三角形的中考题.中考题对于学生而言，似乎有着一定的神秘感，一谈中考题就感觉不简单，为了让学生了解中考题就是稀松平常之题，消除对中考的畏难情绪，本届中考复习，笔者不时采用师生共同编题的活动方式，与学生一同编题，编出中考题，在亲身亲历中，感触中考题的亲近，不是“此曲只应天上有，人间能有几回闻”的高蹈神曲，而是源于我们平民之手的小调，效果明显.

数学教育家威弗赖登塔尔指出：数学知识应由学习者本人去发现或创造，教师的任务是帮助和引导学生进行“再创造”，而不是把现成的知识灌输给学生.复习由于没有统一的文本，老调重弹易沦为平淡，若立足再创造，从“一点、一图、一式”出发等诸如此类，给平静的复习课投以石子，荡起学生思维之涟漪，引导学生通过添加、补充、组合、逆转等手段，不断创编出“新”的问题，然后教师再适时地点化说明，这就是某某市、某某年的中考题，学生的愉悦之情溢于言表，那种积极的情绪会化作向上的力量，推动着学生心悦诚服地去复习，去义无反顾地攻坚克难.这一活动已不是拟一个标题那样的雕虫小技了，是对学生深层情感的挖掘，是对学生创新意识的涵育，具有数学内在的魅力，这种魅力会爆发出学生积蓄已久的思维潜能，形成缤纷异彩的各样题目.

过程设计如下：

环节1：如图14，正三角形是一类常见的三角形，围绕它的试题更是层出不穷，你能设计一个基于正三角形的简单问题吗？（出示正三角形，开放问题）

预设：基于性质与判定两个方面，从边、角、线、对称等角度提出问题.

图14

图15

例如，正三角形的性质有哪些？如何判定它是正三角形？

又如，给定边长，如2，求周长、面积、高线、中线、角分线、中位线、内切圆半径、外接圆半径等.

环节2：通过添线，编出自己的题目，全班交流.

学生成果1：如图15，在正△ABC中，BD是AC边上的中线，延长BC至E，使得CE=CD.

（1）判断△BDE的形状.

（2）若CD=1，求DE的长度及△BDE的面积.

（3）求证：△DCE∽△BDE.

（4）求证：DE2=EC·EB.

（5）作出△BDE的外接圆及内切圆，并在（2）的情况下求出它们的半径.

教学说明：本题的题干就是八上教材第93页的复习题，营造环境唤起了学生的记忆，并立足整个初中学段有了原有基础上的发展性结论，这就是“老题新用”.

学生成果2：在正△ABC中，D、E分别在边BC、AC上，如图16，若AD与BE的交点为O，BD=CE，你还能发现哪些正确结论？

（1）全等形：△BDA≌△CEB，△ABE≌△CAD.

（2）相似性：△AOE∽△ACD，△BOD∽△BCE，△BOD∽△ABD，△AOE∽△BAE.

（3）特殊角：∠AOE=60°.

（4）等积式：AO·AD=AE·AC；BO·BE=BD·BC；AE2=EO·EB；BD2=DO·DA.

（5）特殊图形：O、D、C、E四点共圆；B、D、E、A四点共圆.

教学说明：在笔者的引导下，学生展开广泛的联想，借力以前接触过的问题，形成了一个从全等到相似，从特殊角到特殊图形，从线段相等到等积式等庞大的结论体系，充分发挥了典型图式聚焦核心知识的作用.

图16

学生成果3：P是正△ABC内一点，如图17.

（1）若边长为2，求点P到三边的距离和.

图17

教学说明：正三角形内一点问题是非常常见的问题，问题1钓出了面积法；问题2有一定难度，是对图形旋转变换的深度考查，其实三角形内还有一个很著名的点——费尔马点：到三角形的三个顶点的距离之和最短的点，在中考中时有出现，笔者在此以一道中考题展示，作为对成果3的补充，以延伸题供课后研究，扩大学生视野.

例题（2009年湖州中考题）若P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点P叫作△ABC的费马点.

（1）若P为锐角△ABC的费马点，且∠ABC=60°，PA=3，PC=4，则PB的值为________；

（2）如图18，在锐角△ABC的外侧作等边△ACB′，连接BB′.求证：BB′过△ABC的费马点P，且BB′=PA+PB+PC.

其实，对正三角形而言，费马点就是其中心.

环节3：小结与作业.

小结：理清拟题的基本方法.

必做作业：回顾编题过程，梳理编题常见方法，并完成课堂没有完成好的题目，积累拟题和解题的基本经验.

选做作业：两个正三角形的组合会演绎出哪些题目，请学有余力的同学课后研究.

教学说明：引导学生创编考题，除以上诸多功能外，还有一点需要指出，就是便于知识形成关联，知识进入体系中才会有张力、有魅力.此联有两层含义：一是单元知识的内联；二是相关知识的通联.既然是复习就不要囿于狭小的知识圈地，要前瞻后联，进入初中学段系统，才能把四基盘活.

图18

四、等腰好伴侣——重逢直角三角形（第3课时）

过程设计如下：（思路基本同于等腰三角形）

环节1：（大脑风暴，见图想性）见到图19，同学们能想到哪些相关知识？

图19

预设：判定它是什么图形（从边、角、线三个角度）.它有哪些性质？（边、角、线的基本角度）

边的关系：勾股定理.

角的关系：两锐角互余.

线的关系：三线（高线：射影定理、面积组合、相似模型；中线：斜边中线；角分线：2个等腰模型）与内切圆半径、外接圆半径等.

边角关系：三角函数.

教学说明：恰如笛卡尔之言：“从最简单、最易懂的对象开始，依照先后次序，一步步达到更为复杂的对象.”笔者从一图出发，引导学生广泛联想，然后循边、角、线的基本脉络梳理出来，不仅有利于“弄清家底”，形成稳固的知识基地，而且有助于理解与记忆、便于提取与应用.天文学家开普勒说：“联想是自然奥秘的参与者，是最好的老师.”实践见证了“联想、迁移”的运用之妙，在中考数学复习中发挥了重要的作用，增强了学生学习的主动性，提高了学习效率，优化了学习效果.

环节2：（题组——演练中见证联想）如图20.

（1）若CD⊥AB，垂足为D，则∠ACD与∠B的关系为______，再找出图中的这类关系_______.

（2）若AC=4，BC=3，则AB=______，CD=_____.

（3）若E为AB的中点，且CE=5，则AB=______.

（4）图中有_______对相似三角形，若BC∶AC=3∶4，则BD∶CD=_______，BD∶AD=_______.

（5）若sinA=1∶3，则tanB=_______.

（6）若∠A=30°，BD=1，则△ABC外接圆的半径为_______，内切圆的半径为_______.

（7）若BE平分∠ABC分别交CD、CA于点F、E，如图21，判定△CEF的形状.

图20

图21

（8）在图21的基础上，作EM⊥AD，垂足为M，连接MF，判断四边形CEMF的形状.

（9）在图21的基础上，作CM平分∠ACD交AB于点M，如图22.

图22

求证：（1）FM∥AC；（2）BM2=BD·AB.

教学说明：题组复习，也是笔者的举措之一，通过层层推进、有机关联的题目，把核心的知识技能、方法思想等融于其中，凝聚成一个有机的整体系统链，彰显互补之结构合力，使得题尽其能，聚拢零散于各年级教材中有关直角三角形的知识，以练促思，唤醒记忆.在学生解答后，再返扣以上联想到的性质，形成理论与实践的不断对接，并通过题组中各题目的渐次发展揭示出知识之间的内在关联与综合度，把直角三角形置于整个初中学段系统中，尤其是它与等腰三角形的遥相呼应得到充分展现，这种特殊三角形的自洽见证了直角三角形的核心价值.尤其是后程，立足双垂图，在不断的添线中，一道道靓丽的题目争奇头艳，开满枝头，通过这一核心图把几何的核心知识聚合起来、贯通起来，成为演练的大本营.

限于篇幅，后面的环节略.

一个单元的复习，基本展现了笔者的复习定调，这些举措有了浪漫情怀的底色，使得理性与感性共融，严谨与艺术并存，效果良佳，笔者体会如是，实践证明亦如是.人教社数学室主任章建跃博士论及“应试确实有技巧，但获得技巧的途径有天壤之别.一种是靠大量做题卖苦力，其结果可能是‘讲过练过的不一定会，没讲没练的一定不会’；另一种是靠智慧而实现的‘四两拨千斤’，其结果一定是高奏高考的凯旋之歌.”［1］笔者的以上之为意在追求的是后一种途径.

五、结束语

数学是严谨的科学，但适时来点浪漫的情调也不失一种调剂，一种激趣励志的情绪濡染，可化作复习的强大动力，精神饱满地面对，乐此不疲的复习，效果就在不言中了.我们再次聆听一下苏联教育家卡斯特金的教诲：“未经人的积极情感强化的知识，将使人变得淡漠.由于它不能拨动人的心弦，很快将会被遗忘.”我们若善于融情于知，就容易调度学生的积极情绪参与其中，这种心态将化作向上的力量，火热地、浪漫地完成复习大任，潜移默化中完成德育渗透.

1.章建跃.高分是怎样得来的［J］.中小学数学（高中），2009（09）.H