借“开放探索”专题之力，促初中数学自主复习之效*

2018-03-03广东广州市培正中学

中学数学杂志 2018年4期

☉广东广州市培正中学汤俭

初中数学复习时间紧迫，内容繁多，知识覆盖面广，怎样的自主复习才有效呢？近年来，数学开放探索题在一些中考试题中渐次出现，这类试题题意新颖，构思独特，对思维能力要求较高，它对初中自主复习所产生的积极作用，已愈来愈引起教育工作者的兴趣与重视.

一、开放探索题的含义及其特征

所谓开放探索型问题，是没有明确的条件或结论，没有固定的形式和方法，需要自己确定所需求的结论、条件或方法的一类问题.

正因为开放探索型问题中的条件或结论的不确定性，使得解题的方法与答案呈多样性，这就需要学生在解题过程中有更多的独立和主动思考与探求；要求学生对结论主动做出大胆合理猜想，方能在解题方法上出奇制胜，别出心裁，因而会更有效地激发学生自主复习的主动性和持久性.所以，在初中数学自主复习时，进行开放探索专题复习，相信会大大提高自主复习的有效性.

二、以开放探索专题复习为切入点，探究初中数学自主复习有效学习策略

1.设计条件开放探索型问题，拓展自主复习的宽度.

条件开放探究题是指问题的条件不完备或满足结论的条件不唯一的题型.

解题策略：从结论出发，执果索因，逆向推理，逐步探求结论成立的条件，或把可能产生结论的条件一一列出，逐个分析.

复习关键：在此环节的专题复习中，要注重引导学生的知识联想，把知识点串联起来，实现由量到质的飞跃，达到厚薄间的转化，让学生在联想比较中加强其他知识的综合复习，这既便于记忆，又便于了解它们的内在关联，拓展复习的宽度，提高自主复习的有效性.

例1如图1，OA是△ABC的中线，要使⊙O与AB边相切于点D，与AC边相切，应增加条件________（任写一个），并证明.

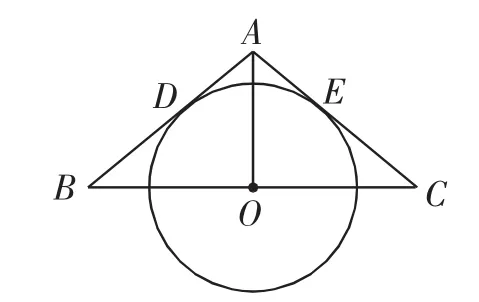
图1

【分析】本例属于条件开放型问题，答案不唯一，可以是∠B=∠C，AB=AC，∠BAO=∠CAO，AO⊥BC等.证明略.

感悟提高：本题考查相切判定的方法，可添加的条件较多，要注意题目中OA是△ABC的中线这一条件.通过本题的复习，可以把圆的切线性质和切线判定方法一并复习和对比分析，找出基本方法（如连半径，得垂直；作垂直，证半径），从而提高复习效率.

2.设计结论开放探索型问题，加大自主复习的广度.

结论开放探究题即在给定的条件下，结论不唯一的题型.

解题策略：从题目条件入手，通过由因执果，通过推理或联想、类比、猜测等方式，获得所求的结论，其中需要运用分类讨论思想，从各个知识不同的侧面入手，进行探索、验证，寻找问题的结论.

复习关键：在复习此类题型时，要注意对例题的条件进行细致有序的分析和推理、联想，有意识地对例题进行一系列改编，达到在挖掘原题的内涵和外延的基础上，在探索中巩固知识、在运动中寻找规律的目的，实现复习的知识从量变到质变，从而提高自主复习的知识广度.

例2 点E、F在△ABC的边AB所在的直线上，且AE=BF，FH∥EG∥AC，FH、EG分别交边BC所在的直线于点H、G.

（1）如果点E、F在边AB上，那么线段EG、FH、AC的长度关系是_________；

（2）如果点E在边AB上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是___________；

（3）如果点E在AB的反向延长线上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是_________；

对（1）（2）⑶三种情况的结论，请任选一个给予证明.

【分析】这是一道探索、确定结论的开放型试题，解决这类问题的方法是根据条件，结合已学的知识、数学思想方法，通过分析、归纳逐步得出结论，或通过观察、实验、猜想、论证的方法求解.

感悟提高：本题考查全等三角形、平行四边形的判定及性质，以及平行线、分线段成比例或相似三角形的性质.在解答结论开放型探究题时，需要通过观察、比较、分析、综合及猜想，展开发散性思维，充分运用已学过的数学知识和数学方法，经过归纳、类比、联想等推理的手段，得出正确的结论.

三、设计组合开放探索型问题，挖掘自主复习的深度

组合开放型问题又称为条件、结论全开放型问题，一般没有明确的条件和结论，需要运用信息发现规律并解答.

解题策略：在解答时，必须认真观察与思考，将已知的信息集中分析，挖掘问题成立的条件或特定条件下的结论，多方面、多角度、多层次探索条件和结论，并进行证明或判断.在自主复习中，教师既能帮助学生梳理知识脉络，分析知识点间的联系，又能加强知识应用和能力训练，提高学生的解题能力.

复习关键：在复习此类题型时，要注意引导学生从不同的角度，采用不同的数学模型，因此在复习时要善于引导学生将习题归类，解决同类问题中的本质性的东西，总结出解这类问题的方法和规律，并对解题思路进行优化与比较，从而挖掘思维的深度，提高自主复习的效果.

例3 如图2，在△ABC和△DEF中，B、E、C、F在同一条直线上，下面有四个条件，请你在其中选择三个作为题设，余下的一个作为结论，写出一个真命题，并加以证明：①AB=DE；②AC=DF；③∠ABC=∠DEF；④BE=CF.

图2

【分析】本例属于组合开放型问题，解答本例时要注意组合的新命题必须是真命题.

感悟提高：本题属于组合开放探索型问题，熟练掌握全等三角形的证明方法是解答本题的关键突破口.同时，这道题的解题入口宽，解题方法较多，学生较易找到解题的切入口，但如何用简洁的方法来解答，这就体现出不同学生的不同思维层次，可见此题是一道既考查基本方法又体现灵活性的题目，对提高学生思维的灵活性和深刻性起到了积极的效果.

通过开放探索题的课堂教学实践，我深深体会到：数学开放探索题专题复习是传统中考复习的一种有益补充，更提高了学生主动进行自主复习的积极性和有效性，它为学生高层次的思维发展提供了一种可能性；它为学生的发展提供了开放、探索的课堂氛围；在教师的专题指导下，让每个学生都能按照自己的思维节奏自由自在地复习，学生能自觉地对已学的知识进行归纳和总结，以形成系统、完整的体系；并能主动强化已经学习的技能、方法和提炼数学思想方法，从而更好地提高自主复习的有效性.