关联同类微专题，铺垫设问助突破——以中考微专题复习为例

☉江苏江阴市青阳第二中学 朱建民

☉江苏江阴市青阳第二中学 陈 雷

中考复习课的选题或学材的精选是每位备课老师首要关注的教研话题.当前，比较流行的做法是围绕知识点进行知识点的梳理，然后跟进一些典型中考试题，再选一些同类习题进行训练.然而有些习题虽然从形式上看属于同一知识点，但是从解题方法、主要难点上看却是另外知识点或方法上的难点.基于以上认识，我们近期尝试构建小专题进行复习，笔者将其定位为“主题关注”，即在某一个方法或知识点的串联下，精选一些同类习题，预设微专题复习进行训练讲评，有望高效地解决这类问题.本文记录一节主题关注“抛物线与直线相切”的考点，供分享和研讨.

一、中考微专题复习课教学简案

教学环节（一） 基础热身.

例1 （1）抛物线y＝x2-x＋m，若其顶点在x轴上，则m＝__________.

（2）在平面直角坐标系中，抛物线y＝x2-3x-4与x轴的交点的个数是________.

（3）若二次函数y＝x2＋2x＋m的图像与x轴没有公共点，则m的取值范围是________.

教学预设：这三道小题分别训练了抛物线与x轴的三种位置关系，利用根的差别式计算求解可以获得解答.为后面相关考题的探究，做好了知识或方法上的预热与准备.

教学环节（二） 考题探究.

例2 如图1，以扇形OAB的顶点O为原点、半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0）.若抛物线y=与扇形OAB的边界总有两个公共点，则实数k的取值范围是_______.

图1

教学预设：解这道题主要是想清三点，第一，抛物线沿y轴上下平移，在平移过程中会与扇形OAB的边界有交点；第二，抛物线经过点B是一次临界状态，把点B的坐标代入抛物线解析式可得k的一个临界值；第三，抛物线与线段OA有且只有一个公共点时，是另一个临界状态，可联立抛物线的解析式与直线OA的解析式，利用根的判别式为0来确定k的另一个临界值.教学时注意观察、发现学生的易错点，即把原点O代入抛物线的解析式求出k=0，需要引导学生辨明这种典型错误，可以通过适当放大图形比例，或通过几何画板动态演示交点个数从直观上获得感知，再从“数”的角度进行精准演算.

例3 在平面直角坐标系xOy中，若点D的横坐标和纵坐标相等，则称点D为等值点.例如点（1，1）、、…都是等值点.已知二次函数y=ax2+4x+c（a≠0）的图像上有且只有一个等值点当m≤x≤3时，函数的最小值为-9，最大值为-1，分析m的取值范围.

教学预设：这是一份中考模考试卷的填空题最后一题，极少数学生能够解决，究其原因，是因为找不到解题的切入口，不知道从何处下手.为了引导学生自主获得思路，我们提出如下一些铺垫问题：

铺垫问题1：题目中的“等值点”有何特征？（预设：这些等值点在直线y=x上）

铺垫问题2：二次函数y=ax2+4x+c（a≠0）的图像上有且只有一个等值点，你想到了什么？（预设：该抛物线与直线y=x相切，即联立两个解析式后，根的判别式为0）

铺垫问题4：当a、c明确之后，问题简化为大家熟悉的下题：

当m≤x≤3时，函数y=-2x2+4x-3（a≠0）的最小值为-9，最大值为-1，分析m的取值范围.（答案为-1≤x≤1）

教学环节（三） 难题突破.

例4（2016年北京海淀区中考二模第29题改编）对于某一函数给出如下定义：若存在实数p，当其自变量的值为p时，其函数值等于p，则称p为这个函数的不变值.在函数存在不变值时，该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地，当函数只有一个不变值时，其不变长度q为0.例如，图2中的函数有0、1两个不变值，其不变长度q等于1.

记函数y=x2-2x（x≥m）的图像为G1，将G1沿x=m翻折后得到的函数图像记为G2.函数G的图像由G1和G2两部分组成，若其不变长度q满足0≤q≤3，分析m的取值范围.

教学预设：这道题十分抽象、晦涩、难懂.我们也预设如下问题，进行铺垫式提问：

铺垫问题1：新定义中提到的所谓不变值，让你想到了什么？（预设：类似上题的等值点，或直线y=x）

铺垫问题2：新定义中的不变长度，你是如何理解的？你能再举一个例子吗？（预设：如果学生不能顺利举例，可以举函数、y=x2为例，安排学生求出它们的不变长度，如果学生有困难，可以先让他们分析出这两个函数的不变值，把y=x代入相应的函数关系式中可求出两个不变值）

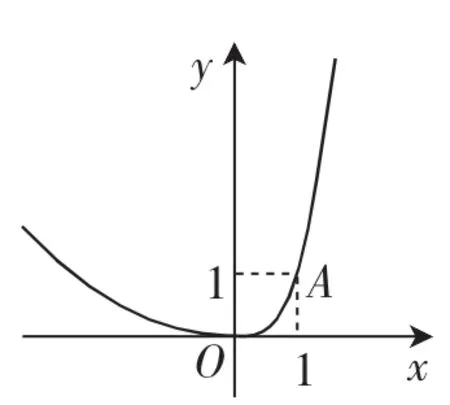
图2

铺垫问题3：先画出函数y=x2-2x的图像（用虚线画图像），明确它的对称轴、顶点坐标，指出它的增减性.举例，用实线画出当x≥1时的函数图像（记为G1）；再将这部分“实像”沿直线x=1翻折，得到图像G2，它们组合成的函数图像G的不变长度是多少？

铺垫问题4：在上一问的基础上，当x≥3时的函数图像记为G1，再将这部分“实像”沿直线x=3翻折，得到图像G2（如图3），它们组合成的函数图像G的不变长度是多少？

铺垫问题5：在上一问的基础上，当x≥4时的函数图像记为G1，再将这部分“实像”沿直线x=4翻折，得到图像G2（如图3），它们组合成的函数图像G有不变值吗？

图3

铺垫问题6：继续画图分析，当x≥0时的函数图像记为G1，再将这部分“实像”沿直线x=0翻折，得到图像G2，它们组合成的函数图像G的不变长度是多少？

铺垫问题7：当x≥-1时的函数图像记为G1，再将这部分“实像”沿直线x=-1翻折，得到图像G2，它们组合成的函数图像G的不变长度是多少？

铺垫问题8：如图4，是否存在某一个m的值，使得翻折后的图像G2恰与直线y=x相切？如何分析出此时m的值？ （预设：设G2的解析式为y=（x-n）2-1，将它与直线y=x联立，利用Δ=0解出n，再算出m的值即可）

图4

教学环节（四） 同类链接.

训练题：（2017年泉州模考题改编）在平面直角坐标系中，我们定义点P（a，b）的“变换点”为Q，且规定：当a≥b时，Q为（b，-a）；当a＜b时，Q为（a，-b）.

已知直线l与坐标轴交于（6，0）、（0，3）两点.将直线l上所有点的变换点组成一个新的图形，记作M.

（1）画出图形M，并直接写出图形M对应的函数解析式；

（2）判断抛物线y=x2+c与图形M的交点个数，以及相应的c的取值范围，请直接写出结论.

教学预设：图形M的图像大致如图5，注意图形M是分段函数图像，对应着直线及y=2x-6.接下来，在分析抛物线y=x2+c与图形M的交点个数时，可想像抛物线从上往下平移过程中，依次与直线x-3相切，此时与图形M有一个交点，接着抛物线会与直线y=2x-6相切，与图形M形成3个交点；当抛物线经过图形M的“顶点”（2，-2）时，又是一次临界状态.

图5

二、关于微专题复习课的教学思考

1.微专题复习课的功夫首先在选题与解题.

微专题复习课的习题不能随便“抓取”，需要在教师大量解题、积累并反思相同结构的考题基础上进行精选，并安排由易到难的顺序渐次呈现.这个过程中，教师日常解题特别是基于大量、长期解题收集的一些素材是十分关键的，平时能否对一些相同或相近结构的考题进行搜集、整理、归类存档，常常是研发高质量微专题的前提.以笔者的经验，对积累丰富的老师来说，有时微专题的选题甚至很快就能从电脑中检索出几个典型问题，并精选几道例题，而这些素材和资源都是平时日积月累形成的.

2.微专题复习课教学的关键是预设铺垫问题.

选题之后，关键是针对较难问题预设恰时恰点的铺垫式问题，就像上文中的一些铺垫式问题一样，针对学生理解新定义、突破难点和易错点处进行设问，通过铺垫问题引导学生学会思考，自主“破题”（史宁中教授语），最终实现问题的解决.而铺垫式问题的预设又需要教师基于深刻理解考题结构的能力，当然，研判学生可能的一些障碍或理解上的难点也是教学预设的必备专业基本功.

1.沈丽婧.聚焦微专题：中考二轮复习的实践与思考——以一组“关联试题”复习为例［J］.中学数学（下），2017（3）.

2.储秀梅.同类跟进：试卷讲评课的一种策略——以一道反比例函数把关题讲评为例［J］.中学数学（下），2017（5）.

3.潘龙生.教学，少些一带而过［J］.数学通报，2015（1）.