基于过程教育的“锐角三角函数（第1课时）”课例及说明

☉浙江省宁波市江北区实验中学 杨红芬

一、背景介绍

《义务教育数学课程标准（2011年版）》（以下简称《课标》）根据数学具有过程和结果的双重性特征，倡导统筹兼顾过程与结果.但以浙教版《数学》九年级下册1.1节“锐角三角函数（第1课时）”为载体的“多人同课异构式”的研修活动发现，课堂教学普遍存在过程教育不到位的问题，主要表现在：有些教师没有按归纳方式定义的概念来针对性地设计教学，有些教师的教学没有侧重点——有对几个概念平均使力的现象，大多数教师在用概念解决问题的教学中缺乏变式与拓展，导致没有全面发挥涉及内容的育人功能.鉴于此，笔者在重复式观课与反思基础上，对该课的教学进行了重建与实践，改进后的课例得到了专家的认可.现整理成文，与读者交流分享.

二、教学实录

环节1：经历回顾旧知并提出问题的过程——明确研究问题

师：我们知道，直角三角形有三边之间的关系（勾股定理）和两个锐角之间的关系（两锐角互余）.我们也知道，含有30°、45°、60°的直角三角形有边之间的关系.例如，30°所对的直角边等于斜边的一半.现在请大家解决下列问题.

问题1：如图1，在△ABC中，已知∠A=30°，AB=4，∠C=90°.问：BC=？AC=？

图1

师：你是怎样计算的？

生1：先用30°角所对的直角边等于斜边的一半求出BC，再用勾股定理求出AC.

师：好的.若∠A=45°呢？∠A=60°呢？

师：好的.若∠A=30°，BC=1呢？

师：这说明，在Rt△ABC中，当∠A=30°或45°或60°时，已知一边能求出其他两边.

问题2：如图2，若一根4m长的竹竿AB斜靠在墙上，则竹竿的倾斜程度可用竹竿与地平面所成角的度数来刻画.如果端点B离地面的高度BC长为1m，除测量外，怎样求角α的度数？

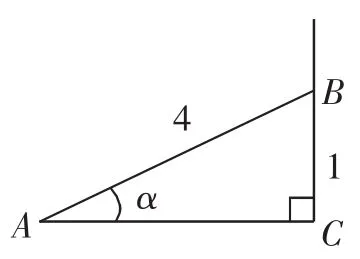
图2

师：看来还无法解决这个问题.本节课我们就来研究解决这样问题的方法.（揭示课题）

环节2：参与定义锐角三角函数的活动——形成锐角三角函数概念

师：现在请大家计算并思考下列各题.

（1）如图3，∠A=30°，BC⊥AC于点C.若AB=3，则=？若AB=2呢？由此，你发现了什么？

（2）如图4，∠A=45°，BC⊥AC于点C.若AB=3，则=？若AB=2呢？由此，你发现了什么？

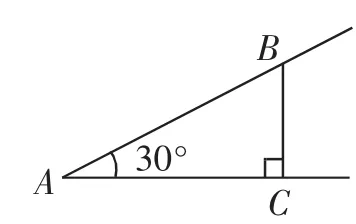
图3

图4

图5

（3）如图5，∠A=60°，BC⊥AC于点C.若AB=3，则=？若AB=2呢？由此，你发现了什么？

（约3分钟后）

师：谁来回答第（1）小题？

师：好的.一般地，如图6，当∠A=α时，B1是AB上的任意一点，则吗？

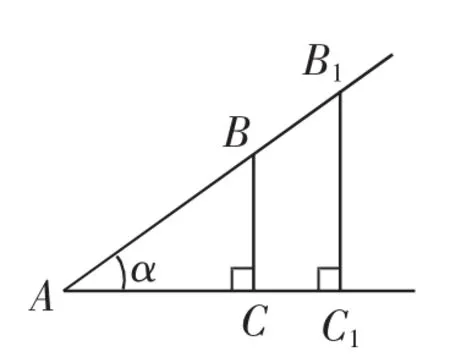
图6

11成比例.

师：好的.你用相似三角形性质来说明.这样，如图6，对于每一个确定的锐角α，在角的一边上任取一点B，作BC⊥AC于点C，比值都是一个确定的值.

师：好的.为以后研究和叙述方便的需要，我们给这样的函数一个名称：如图6，我们把比值叫作∠α的正弦（sine），记作sinα，即sinα=例如，当∠α=30°时，有sinα=sin30°=；当∠α=45°时，有sinα=sin45

师：这里sinα，cosα，tanα都是一个完整的符号，单独的“sin”没有意义.其中α前面的“∠”一般省略不写.锐角α的正弦、余弦和正切统称α的三角函数.

师：如图7，若∠A是Rt△ABC的一个锐角，则sinA，cosA，tanA分别是什么？

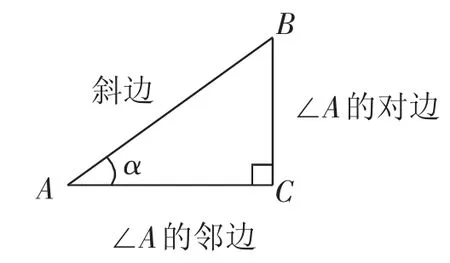
图7

师：好的.根据图7，能说说sinα，cosα的取值范围吗？

生10：因为直角三角形的边长都是正数，所以sinα＞0，cosα＞0.又因为直角三角形的直角边长小于斜边长，所以sinα＜1，cosα＜1.从而0＜sinα＜1，0＜cosα＜1.

师：有道理.tanα的取值范围是什么？

生11：由图7可知，tanα＞0.

师：不错.锐角三角函数的概念揭示了直角三角形中的边角关系，运用它能解决与直角三角形有关的度量问题.

环节3：参与尝试概念应用的活动——合作解决有代表性问题

师：现在请大家解决下列问题.问题3：如图8，在Rt△ABC中，∠C=90°，AB=5，BC=3. 问：∠A的正弦值、余弦值和正切值分别是什么？

生12：因为AB=5，BC=3，所以根据勾股定理，得AC=所以sinA=

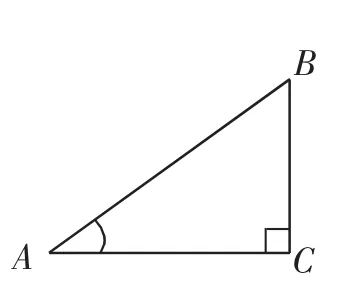
图8

师：不错.∠B的正弦值、余弦值和正切值分别是什么？

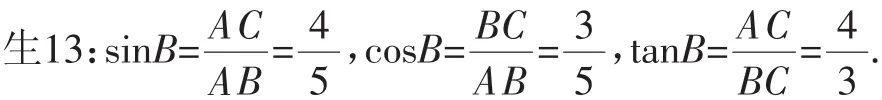
师：好的.由此，大家发现了什么？

生14：sinA=cosB，cosA=sinB，tanA×tanB=1.

生15：（sinA）2+（cosA）2=1.

师：太有才了！大家课后可以继续探索，这些关系是成立的.

师：如图8，在Rt△ABC中，∠C=90°.若sinA=能求

师：这种设法体现了化归思想，以后会经常用到.如图8，在Rt△ABC中，∠C=90°，AB=5，tanA=能求BC和AC吗？

师：你的解法也体现了化归思想.大家通过解答上述问题，获得了哪些经验？

生18：解题后要继续提出新问题.

生19：解题后要善于观察、猜想.

生20：已知比值，可用“设k法”，将未知的边转化为“已知”.

师：不错.解题后的反思，能加深对给定问题的认识和积累解题经验.

（接下来，要求学生完成课本中的练习题，并待学生完成任务后进行交互反馈与评价）

环节4：参与回顾与思考的活动——合作进行反思与总结

师：本节课研究了哪些内容？

生21：本节课研究了锐角三角函数概念及其应用.

师：获得锐角的正弦经历了哪几个步骤？

生22：计算比值→归纳概括→定义表示.

师：好的.“操作观察、归纳概括、定义表示”是概念学习的基本经验.

师：求特殊角的三角函数值有何经验？

生23：由于“比值”与动点的位置无关，所以求“比值”可用取特殊值的方法.

师：这是有价值的经验，请大家课后依据此经验求sin60°、cos60°和tan60°.

师：大家认为对于锐角三角函数还可以继续研究什么？

生24：像研究一次函数一样，还可以研究锐角三角函数的图像、性质及其应用.

师：有道理.锐角三角函数的图像与性质，以及生25所说的这些函数待高中阶段研究，初中阶段只研究锐角的正弦、余弦和正切的概念，旨在解决与直角三角形有关的度量问题.

生26：怎样解决问题2？

三、教学说明

过程教育是指旨在促进学生全面、和谐发展的需要，关注数学结果形成、应用的过程和获得数学结果（或解决问题）之后反思过程的育人活动.它不是偏面强调过程，而是根据数学结果的地位与作用，以及获得数学结果（或解决问题）的过程和所蕴含的数学思想方法的价值确定过程与结果的平衡点.其基本要求是：教学内容全面，认知过程完整，教学方法和谐.［1］

“锐角三角函数（第1课时）”的教学内容不仅包括锐角三角函数概念，也包括锐角三角函数概念的形成、应用的过程和所蕴含的数学思想、数学活动经验.锐角三角函数的教学性质是概念教学，由于该概念比较抽象，并且概念的形成过程有较大的教育价值，所以该概念宜采用归纳的方式定义.锐角三角函数是认识直角三角形的继续，也是认识函数的继续，它是进一步学习三角函数的基础，是解决与直角三角形有关的度量问题的重要工具；其具体到抽象和特殊到一般的研究方法在教学实践中具有普适性.实践告诉我们，定义锐角三角函数的过程和蕴含的变化与对应思想、归纳思想、演绎思想、符号表示思想、类比思想等，用锐角三角函数解决简单问题的过程和蕴含的数形结合思想、化归思想等，这些对发展学生的智力、能力和个性有积极的作用.《课标》中课程内容对该课提出的教学要求是“利用相似的直角三角形，探索并认识锐角三角函数（sinA，cosA，tanA），知道30°，45°，60°角的三角函数值，能用锐角三角函数解直角三角形”.在教师适度引导下，学生求30°，45°，60°角的三角函数值和用锐角三角函数解直角三角形的难度不大，但探索并认识锐角三角函数对学生来说有一定的难度.

本课例根据锐角三角函数的教学性质及其地位与作用和所蕴含的教育价值，用“归纳”的方式定义锐角的正弦，用类比的方式给出锐角的余弦和正切，针对性地设计了“提出问题→定义锐角的正弦（操作观察→归纳概括→表达概念）→用类比的方法定义锐角的余弦和正切→解释直角三角形中的边角关系→解决问题→反思内化”的教学过程，并把教学的侧重点放在定义锐角的正弦和“解决问题”上，以突出锐角的正弦，感悟研究的过程和所蕴含的数学思想、积累解决直角三角形中边角关系问题的经验.教学采用了“以教材提供的题材为载体，从学生已有的知识与经验出发，运用教师价值引导与学生自主建构相结合的适度开放的方式，引导学生经历完整的认知过程”的方法，以“激发学生的学习兴趣”“引发学生积极思考”“培养学生良好的数学学习习惯”“使学生掌握恰当的数学学习方法”.［2］

浙江省数学特级教师邬云德老师认为，该课例遵循了概念（用归纳形式定义的概念）教学的基本规范，体现了过程教育和以学为中心的思想，可以实现“能结合图形陈述锐角三角函数概念，会用符号表示锐角三角函数，能知道锐角三角函数值的取值范围，能感悟锐角三角函数概念的形成过程和所蕴含的抽象思想、变化与对应思想、归纳思想、类比思想等；会用锐角三角函数定义求锐角三角函数值”的教学目标，它对发展学生数学核心素养和帮助教师理解与实践基于过程教育的概念（用归纳形式定义的概念）教学方法有积极的影响.

1.邬云德.旨在统筹兼顾过程与结果的过程教育理论［J］.中学数学（下），2017（11）.

2.史宁中.义务教育课程标准（2011年版）教师学习指导（初中数学）［M］.北京：北京科海电子出版社，2011.H