含损伤板的动载荷识别精度研究

周 凤，缪炳荣，陈翔宇，王名月，杨忠坤

(西南交通大学 牵引动力国家重点实验室，成都 610031)

近年来，线性结构和非线性结构动力学的系统辨识和载荷识别问题在轨道车辆的结构健康监控研究中已经得到广泛的关注与重视，载荷识别问题属于结构动力学的第二类逆问题，研究内容可分为动载荷值的识别和载荷作用位置的识别[1–5]。动载荷识别方法主要集中在频域法和时域法两种，频域法研究较早，现已趋于成熟，而相对于频域法，时域法的研究工作开展得较晚。但由于时域法不仅适用于线性系统，对于非线性系统且对冲击载荷等瞬时激励的反求问题有较好的处理效果，因此时域方法越来越受到学者们的关注。

Doyle利用反卷积的方法反求梁和板结构的冲击外载荷，同时用光滑的三角波作为基函数，用小波变换反求，所得的效果很好[6]。初良成等对于离散系统的动态载荷识别提出了一种新的时域分析方法，用正分析的手段求解反问题，在实测信息自由度数不少于待识别荷载自由度数的前提下，该方法克服了识别精度受测量信息数目限制的缺点[7]。周盼等在对各种时域方法进行了概述与总结，并分析了各自的优缺点[8]。另外，随着科学技术的不断发展，载荷识别研究方面也涌现了很多新的技术。Matthew S.Allen和Thomas G.Carne提出了利用来自多个时间步数据的鲁棒性逆向结构滤波器（ISF）力重建算法的扩展，同时提高了ISF算法的精度[9]。将所提出的算法延迟多步ISF（DMISF）算法，与原始ISF和加权加速度技术（SWAT）和经典频域（FD）逆方法的总和在前向建模误差的精度和灵敏度方面进行比较。毛玉明等提出了基于灵敏度分析法的结构动载荷识别技术[10]。将结构输入载荷进行参数化，通过灵敏度迭代分析来确定相应的载荷参数,从而确定结构的动态输入载荷。Y.E.Lage等利用位移传递性概念来识别作用在结构上的载荷，通过数值模拟和实验验证了该方法的有效性[11]。Xiaowang Li和Zhongmin Deng提出了一种基于2阶泰勒级数扩展的新方法，用于识别时域中的结构动态载荷[12]。该算法将响应向量表示为泰勒级数近似，然后推导出一系列公式。数值仿真结果表明，无论响应是否被噪声污染，所提出的方法可以获得更准确的识别力时间历程。

载荷重建与损伤识别都是结构健康检测中的关键问题。然而，对于载荷和损伤共存的情况似乎没有太多的研究，尽管实际工程中两者经常同时存在。Qingxia Zhang等提出了一种基于虚拟变形方法来研究载荷和损伤共存的问题[13]。损伤的结构由相同的完整结构来建模，受到相同的负载，对有损伤的模型进行虚拟变形。测量的结构响应用于识别载荷，并确定了损伤的类型和程度。

因此，本文在时域正演法的理论基础上，考虑损伤对载荷识别精度的影响，并比较不同的测点组合下反演载荷的结果。通过优化传感器位置、选择不同的测点，识别精度将得到较大提高。

1 理论背景

以一个n自由度比例阻尼系统为研究对象，其运动微分方程为

式中M，C，K分别为总体质量矩阵、阻尼矩阵和刚度矩阵；f(t)为载荷列向量；分别为位移、速度和加速度响应向量；设受到k个待识别载荷f(i，t)(i=1，2，...，k)的作用，其对应结构自由度序号为g(i)，另设l个实测响应为x(i，t)，(i=1，2，...，l)（可以为位移响应、速度响应或加速度响应），其对应的自由度序号为h(i)。由有限元分析求得前m阶模态wr，φr(r=1，2，...，m)。

由振型叠加法，得

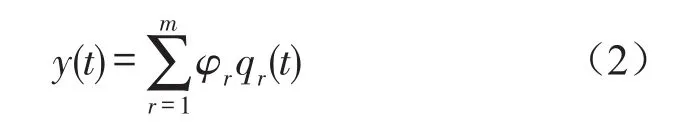
cr=2mrwrξr，r=1,2,…,m

设在区间[0，T]上识别外荷载f(l，t)(l=1，2，…，k)，并在时间t∈[0，T]上采用如下等间隔划分

(j=1，2，…，s-1)，t∈[tj，tj+1]，Prj为1阶跃力，在t∈[tj,tj+1]上对（3）式应用杜哈梅积分，则有

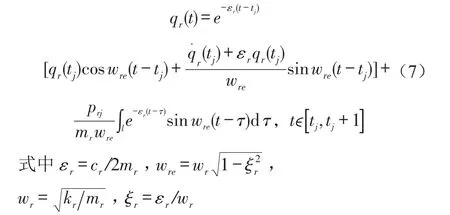
计算（7）式中的积分项，并对qr(t)两次微分得

式（8）、式（9）、式（10）中

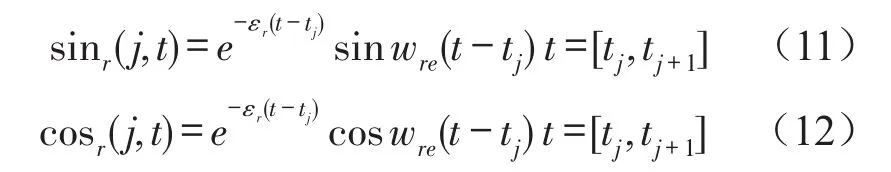
当t=tj+1时，令

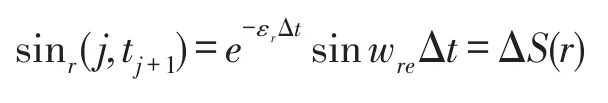
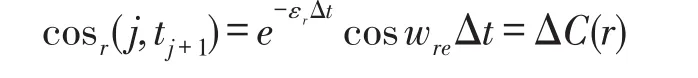
在式（8）中令t=tj+1，整理得

利用式（8）、式（9）可推出如下公式

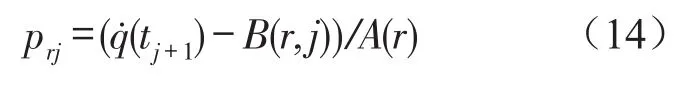
其中j=1,2,…,s-1

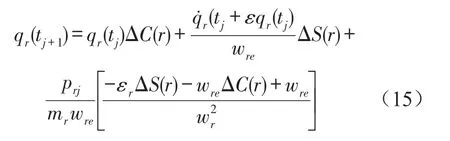
由式（2）式可得

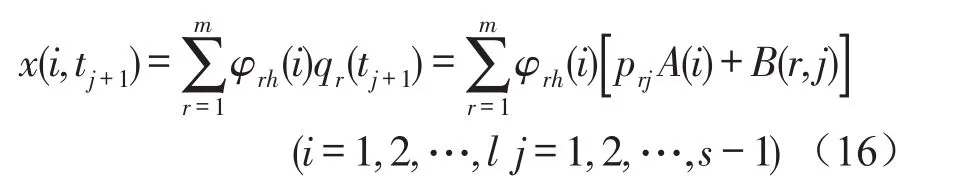
将式（6）代入式（16）中，并整理得

由式（15）得

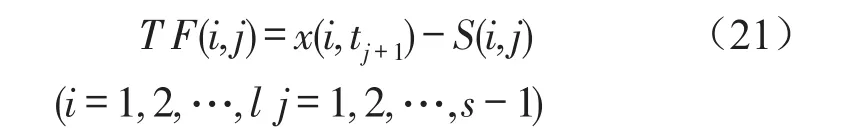
在零初始条件下有qr(t1)r(t1)=0（r=1,2,....,m)。依次应用式（13b）、式（19）、式（21）可求得TF(i,l)(i=1,2,…,l)，然后由式（20）可求得f(l,1)(l=1,2,…,k)的最短范数的最小二乘解。由式（15）、式（12）及式（6）式可得

其中i=1,2,…,m；j=1,2,…,s-1

重复应用式（13b）、式（14）、式（20）、式（22）便可依次求得f(i,j)。

若x(i,tj)为速度或加速度时，推导过程与上过程x(i,tj)为位移时的相同。

2 算例

2.1 算例1

矩形薄板的损伤模型如图1所示，其参数如下：板长200 mm，宽200 mm，厚4 mm，弹性模量为7.2×1010Pa；泊松比为0.3；密度为2 700 kg/m3。为了模拟结构损伤，假定损伤处的弹性模量降低了50%。

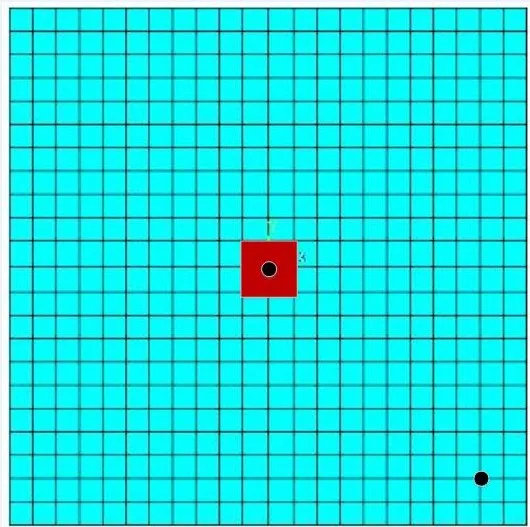
图1 损伤模型（红色矩形为损伤部分，黑色圆点为加载位置）

分别考虑在损伤处和非损伤附近施加载荷，进行载荷识别。假设所施加的激励都为垂直于平板方向z向上的正弦激励Fz(t)=-sin(2πt)（单位为N），动态载荷的时间历程如下图2所示

图2 激励力时程曲线

2.1.1 损伤对模态的影响

利用ANSYS有限元软件进行模态分析，分别得到有损伤板和没损伤板的前5阶固有频率，如表1所示。

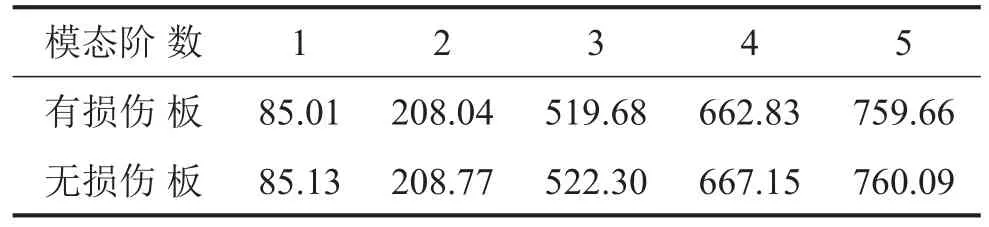
表1 固有频率/Hz

由上表1可知，损伤板和无损伤板的固有频率相差很小，所以损伤对结构模态频率的影响是很小的。

2.1.2 非损伤处施加载荷

在板的非损伤附近施加载荷，所得的识别效果如图3所示。

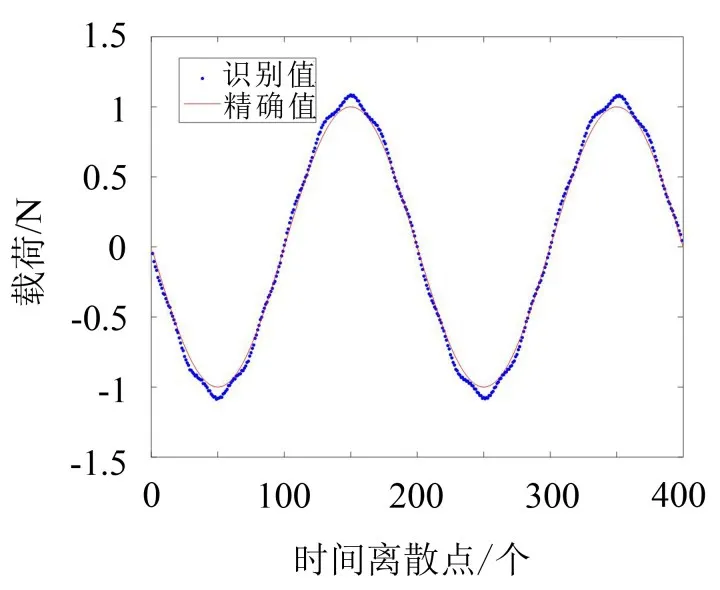
图3 非损伤处载荷识别结果

由图3可以得到，该识别方法对于非损伤处施加的激励能高精度的识别，识别效果好。

2.1.3 损伤处施加载荷

利用时域正演法反演损伤处所加的激励，识别结果如下图4。

图4 损伤处载荷识别结果

由上图可知，损伤处的识别效果并不理想，峰值误差较大，这是因为当结构发生局部损伤时，结构刚度降低。但整体的识别趋势较好，曲线光滑度好。

2.2 算例2

图5为一中间开孔的薄板有限元模型和节点示意图，其主要参数如下：长×宽×厚：200 mm×200 mm×5 mm；内方孔边长为20 mm；所采用的材料与算例1相同；边界为一端自由，另一端固定。

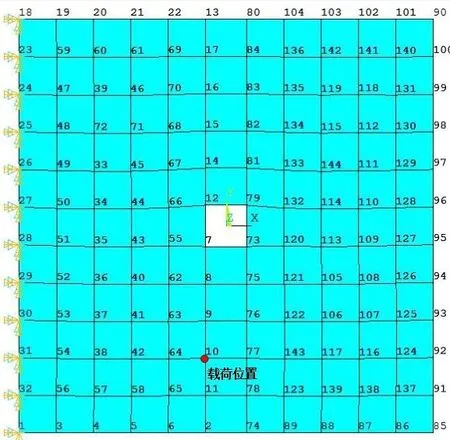
图5 薄板的有限元模型

在板的节点10处施加如上图2的正弦激励，测量的响应为垂直于平板方向的位移，利用有限元分析可求得结构的位移响应，并以此作为实际采样值，应用时域正演方法进行载荷识别。正弦部分的识别效果用相对误差来评定，误差的判别式如下

利用不同测点组合的位移响应，选用不同的模态数反演节点10所加的载荷。由于该方法识别精度不受测量信息数目的限制，因此每次选择三个测点。采用不同的测点组合，即11、77、78测点，117、138、139测点，96、127、128测点，112、130、131测点，101、140、141测点，分别记为A、B、C、D、E。

因此，各测点组合在不同模态阶数和不同时间点数识别的误差见表2。

2.2.1 测点位置对识别结果的影响

表2中测点组合A、B、C、D、E的识别误差，即是离激励点逐渐远的测点识别的误差，可以看出在离激励点越远的地方识别的误差很大，最远的E组合误差高达了50%左右，识别效果随着测点离激励点的距离不断变差。这说明传感器的布置对于载荷识别结果影响很大，应将测点布置在离激励点稍微近的地方，在一定范围内能较好的识别，但一定不能太远，否则识别误差很大。

2.2.2 采样时间间隔对识别结果的影响

在其他条件不变的情况下，改变采样时间步长进行载荷识别。即考虑在10节点施加激励，利用测点117、138、139在3阶模态下的不同采样时间间隔对载荷识别的影响。表3列出了不同采样时间间隔下的峰值识别误差。

从表中的误差数据可以看出，当采样时间间隔从0.01降低到0.005时，误差明显减少，识别精度显著提高；但当采样时间间隔从0.005降低到0.002时，误差值降低得不明显，识别精度也差不多。这说明在一定的频率范围内降低采样时间间隔对提高识别精度是有作用的。

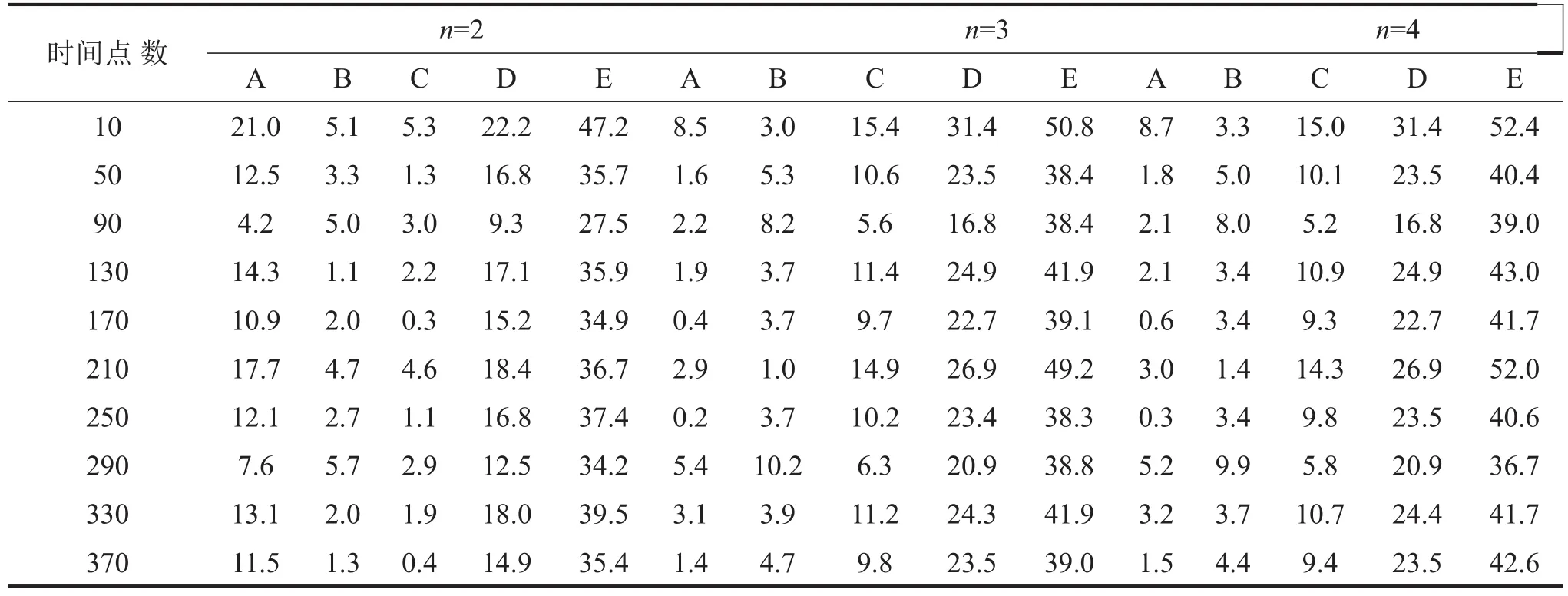
表2 不同模态阶数（n）下不同测点位置的识别误差/（%）

表3 不同采样时间间隔下的识别误差

3 结语

基于时域正演法的识别原理，分别研究损伤、测点位置和采样时间间隔对识别精度的影响。结合仿真结果，可以得出以下结论：

（1）在该识别方法基础上，当加载位置不是位于损伤附近，选择合适的测量点仍能较准确识别出施加的激励，但当加载位置位于损伤处时，识别结果较差，这是由于结构损伤所带来的非线性影响。因此在研究有损伤情况下的载荷识别，需改善识别原理或提出一种新的方法。

（2）不同的测点位置和采样时间间隔，所得到的识别结果误差是不一样的。

（3）合理布置传感器位置和选择合适的采样时间间隔，即在激励点的一定距离范围内和较小的采样时间间隔，能够明显提高载荷识别精度和计算效率。

[1]E LOURENS,E REYNDERS,G DE ROECK,et al.An augmented Kalman filterforforce identification in structural dynamics[J].Mechanical Systems and Signal Processing,2012,27:446-460.

[2]Y DING,S LAW,B WU,et al.Average acceleration discrete algorithm for force identification in state space[J].Engineering Structures,2013(56):1880-1892.

[3]伍乾坤，韩旭，刘杰，等.一种直接求解的动态载荷识别方法[J].应用力学学报，2011(2)：201-205+218.

[4]Z SHARIF-KHODAEI,M GHAJARI,M ALIABADI.Determination of impact location on composite stiffened panels[J].Smart Materials and Structures,2012,21(10):105026.

[5]祝德春，张方，姜金辉.动态载荷激励位置识别技术研究[J].振动与冲击，2012，(01)：20-23+48.

[6]J F DOYLE.A wavelet deconvolution method for impact force identification[J].Experimental Mechanics,1997,37(4):403-408.

[7]初良成.动态载荷识别的时域正演方法[J].应用力学学报，1994，11(2)：xxx-xxx.

[8]周盼，张权，率志君，等.动载荷识别时域方法的研究现状与发展趋势[J].噪声与振动控制，2014，34(1)：6-11.

[9]M S ALLEN,T G CARNE.Delayed,multi-step inverse structural filter for robust force identification[J].Mechanical Systems and Signal Processing,2008,22(5):1036-1054.

[10]毛玉明，郭杏林，赵岩，等.基于灵敏度分析的结构动态载荷识别研究[J].振动与冲击，2010，29(10)：1-3+247.

[11]Y LAGE,N MAIA,M NEVES,et al.Force identification using the concept of displacement transmissibility[J].Journal of Sound and Vibration,2013,332(7):1674-1686.

[12]X LI,Z DENG.Identification of dynamic loads based on second-order taylor-series expansion method[J].Shock and Vibration,2016:1-9.

[13]Q ZHANG,Ł JANKOWSKI,Z DUAN.Identification of coexistent load and damage[J].Structuraland Multidisciplinary Optimization,2010,41(2):243-253.