基于模糊滑模backstepping的半主动空气悬架设计

孙丽颖，王君莹

（辽宁工业大学 电气工程学院，辽宁 锦州 121001）

悬架系统是维持车辆乘坐舒适性和操作安全性的最重要的部分之一，它能隔离路面冲击对车身的影响，从而保证车辆的行驶性能。一般来说，悬架分为三种：被动悬架、半主动悬架、主动悬架[1]。由于被动悬架的参数一经确定是不可调节的，因此在改善悬架性能方面受到很大限制。主动悬架在被动悬架的基础上增加了动力源，从而使悬架的结构变得复杂、成本提高，不易普及。半主动悬架是一种可以调节刚度或者阻尼的无源主动悬架，结构简单、造价低廉，使其在实际中应用广泛。作为一种将空气弹簧作为弹性元件的悬架系统，空气悬架的固有频率低、刚度可变、振动及噪声小等优点使其受到广泛的关注。由于空气悬架系统是一个复杂的非线性系统，悬架的刚度、阻尼系数等参数会随着车辆的载荷、车速、路况的变化而变化，因此如何设计出满足各种工况而且能使车辆的行驶平顺性、乘坐舒适性和操作安全性处于最佳状态附近很重要。近年来，在研究空气悬架问题上，使用较多的控制策略是PID控制[2–3]、模糊控制[4]、神经网络控制等[5]。

自从1991年著名学者Kokotovic提出backstepping方法[6]之后，它就引起了许多学者的极大关注，已经逐渐成为处理非线性问题的有效手段。文献[7]主要研究了带有约束的主动悬架系统。文献[8–10]采用自适应backstepping方法设计了控制器，使悬架的垂向振动有了明显改善。文献[11]采用backstepping方法设计了积分滑模控制器，用一个高增益状态观测器来估计系统中的不确定参数和干扰。文献[12]在backstepping控制的基础上加入滤波参数可调的非线性滤波器，有效提升了车辆舒适性和操纵稳定性。文献[13]应用自适应backstepping方法设计了一个的新型容错控制器，大幅度提高系统的稳定性能。

本文将针对1/4二自由度半主动空气悬架系统，考虑阻尼系数的非线性不确定性问题，用模糊系统进行逼近，同时结合backstepping和滑模控制方法设计控制器，提高系统的收敛性能，尽量减小簧载质量垂向加速度、悬架动行程、轮胎动载荷。

1 模型建立

悬架系统模型的建立是分析和研究系统性能的基础。在研究车辆的操作稳定性和乘坐舒适度时，悬架通常被简化为一个复杂振动系统。悬架模型的建立大致有3种：整车模型、半车模型、1/4车模型。本文选择建立1/4自由度模型，为了研究方便，做出以下假设[14]：

（1）车身和车轮都是刚体，不会发生形变；

（2）把悬架系统看作是并联的线性弹簧和阻尼器，文中只考虑空气弹簧的刚度变化；

（3）车轮始终与地面接触且只有刚度没有阻尼力，并可简化为线性弹簧。

由牛顿第二定律可得到半主动空气悬架系统的运动微分方程

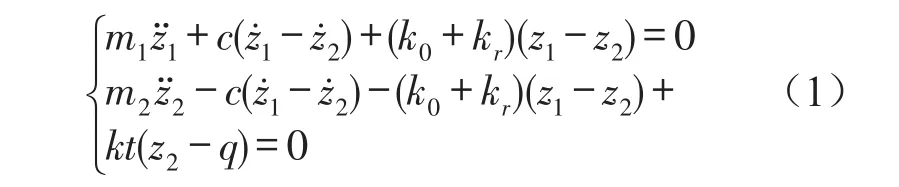
式中m1为簧载质量；m2为非簧载质量为簧载质量的垂向加速度为非簧载质量的垂向加速度；为簧载质量的垂向速度为非簧载质量的垂向速度；z1为簧载质量的垂向位移；z2为非簧载质量的垂向位移；q为路面激励；c为悬架阻尼系数；kt为轮胎的等效刚度；k0为半主动空气悬架的基值刚度；kr为半主动空气悬架的可调刚度。

考虑到阻尼器的减振系数随着行程的伸张而变大，随着行程的压缩而变小，所以它不是一个固定的常值 ，因此将看成不确定函数 ，用f2(∙) 表示。令u=kr(z1-z2)当作系统的控制输入，下面进行坐标变换：所以式（1）可变为

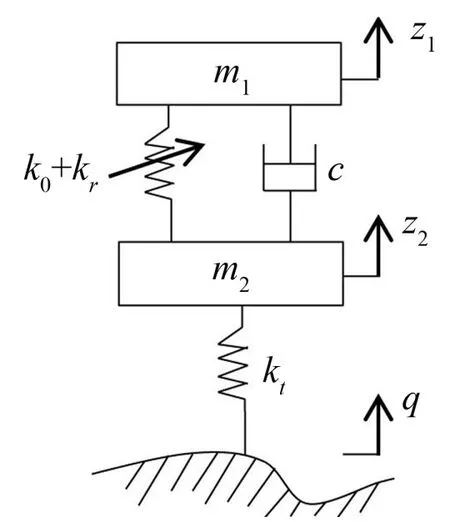
图1 1/4二自由度半主动空气悬架模型

本文用模糊逻辑系统来逼近未知函数f2(∙)，通过间接模糊自适应backstepping方法构造Lyapunov函数，通过设计控制量u在保证系统稳定的同时，尽可能地提高悬架性能。模糊逻辑系统选取的一般形式为其中θΤ∈Rn是调节参数向量，ξ(∙)是模糊系统中的基函数，对于一个给定的连续函数f(∙)，在有界闭区间Ω内，存在一个理想的可调参数向量θ∗，使其对于任意的ε＞0，满足其中

2 控制器的设计

[15]可知，选择合适的被控变量可以避免不稳定的零动态特性。下面采用backstepping方法对系统（2）设计控制器。

第一步：首先，定义误差变量

其中x1是车身的垂向位移，xˉ3是经过滤波器的车轮垂向位移变量，定义

b是常数，对于系统（2.1），把x2看作虚拟控制，取镇定函数

其中c1是一个正常数，则可得

定义误差变量e2=x2-x2d，因此

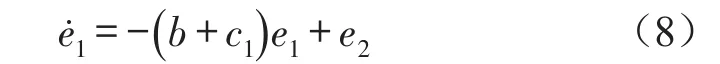
取第一个子系统的Lyapunov函数为

第二步：在真实控制即将出现的时候，定义滑模面s=k1e1+e2，其中，k1为待设计的常数。由于f2(∙)是未知函数，需要用模糊逻辑系统去逼近f2(∙)，定义ε=f2(∙)-θΤξ(∙)，其中ε为f2(∙)和理想模糊系统的差值，θ͂=θ-θ̂，θ̂为θ的估计值，θ͂为估计值与实际值之间的误差。选取系统的Lyapunov函数

γ＞0是待设计参数，则

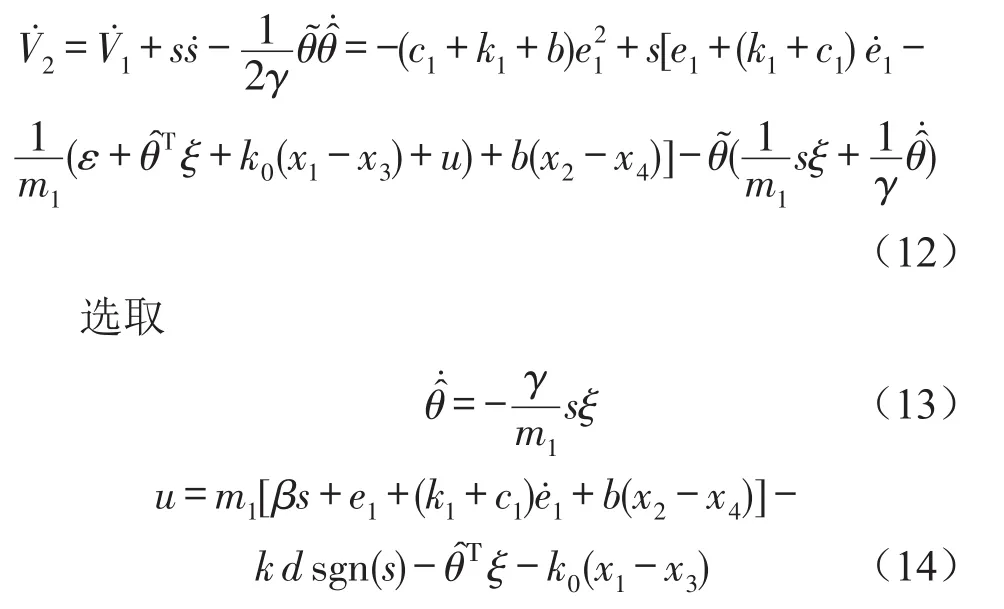
其中kd＜inf|ε|，β为待设计的常数，把上式代入(12)中得

因此误差系统可以表示为

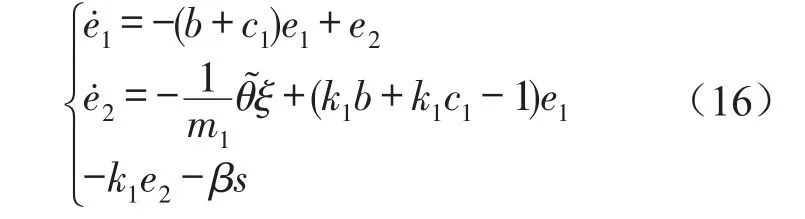
因此系统式（2）在控制律式（14）和参数替换律式（13）的作用下，误差系统式（16）在原点处是渐进稳定的。

3 仿真分析

为了验证控制器的有效性，特采用MATLAB/Simulink软件进行仿真验证。定义模糊基函数

令ξ(x)=[ξ1(x)，ξ2(x)，ξ3(x)，ξ4(x)，ξ5(x)]T，从而可以得到模糊逻辑系统

模糊隶属度函数为

图2 路面随机输入

悬架系统的仿真参数的选取如表1所示。控制器的参数选取：c1=100，b=1.5，k1=100，β=10，kd=0.1，γ=10。

表1 悬架结构参数

图3、图4、图5分别为簧载质量加速度、悬架动行程、轮胎动载荷的响应曲线，其中实线表示模糊滑模backstepping控制方法的半主动空气悬架的响应曲线，虚线表示被动悬架的响应曲线。

为了验证模糊逻辑系统的逼近的效果，假设阻尼系数发生改变，c=1 200 N∙s/m，其他参数不变，车辆在随机路面激励下的响应曲线如图6、图7、图8所示。

从表2中可以看出，本文所设计的控制器在随机路面上能有效地改善车辆的性能。与被动悬架相比，采用了模糊滑模backstepping控制方法的悬架系统的簧载质量加速度和轮胎动载荷均方根值分别减少了70%、5%，悬架的动行程为2 cm，保持在安全范围内。当阻尼系数发生变化时，模糊逻辑系统能有效逼近非线性函数，解决了不确定性参数问题。

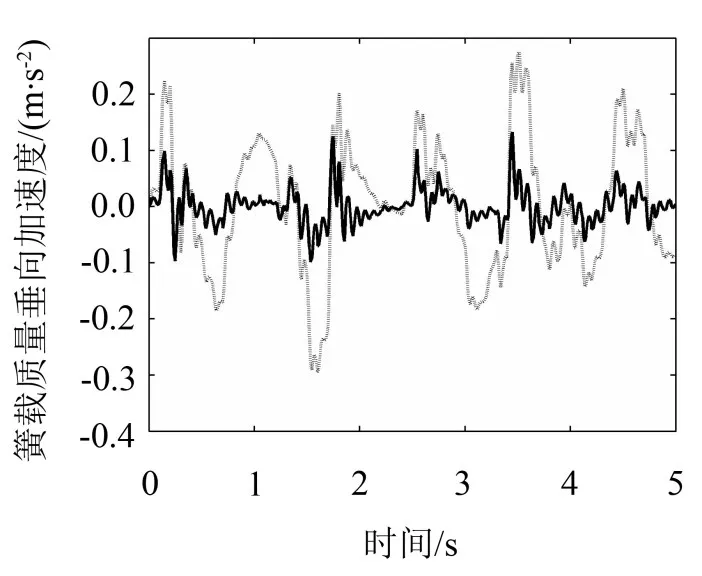
图3 簧载质量加速度

图4 悬架动行程

图5 车轮动载荷

4 结语

本文以簧载质量加速度、悬架动行程、轮胎动载荷为评价指标，基于1/4二自由度半主动空气悬架动力学模型，考虑了阻尼系数的非线性不确定性，用模糊逻辑系统逼近非线性不确定函数，设计了模糊滑模backstepping控制器，并通过MATLAB/Simulink软件进行了仿真验证。结果表明，与被动悬架相比，本文所设计的控制器能够有效改善车辆的乘坐舒适度和操作安全性，当不确定参数发生变化时，控制性能并没有变差，说明了本文设计的控制器的有效性。

图6 参数改变后的簧载质量加速度

图7 参数改变后的悬架动行程

图8 参数改变后的车轮动载荷

表2 仿真结果性能指标对比

参考文献：

[1]YAGIZ N,HACIOGLU Y.Backstepping control of a vehicle with active suspensions[J].Control Engineering Practice,2008,16(12):1457-1467.

[2]M LI,Z LI,X SHEN,et al.Study on PID control for semiactive air suspension for riding comfort[C].2010 Second WRI Global Congress on Intelligent Systems.Wuhan,IEEE,2010:47-50.

[3]YANG N.Research on air suspension system based on pid control[C].International Conference on Intelligent Humanmachine systems and cybernetics.hangzhou,IEEE,2013:106-109.

[4]赵永胜，刘志峰，蔡力钢，等.基于模型参考的主动空气悬架模糊自适应滑模控制[J].机械科学与技术，2010，29(1)：12-16.

[5]常盛，王福明，CHANG Sheng，等.基于改进BP神经网络的空气悬架控制研究[J].制造业自动化，2013，35(9)：119-122.

[6]KANELLAKOPOULOS I,KOKOTOVIC P,MORSE A S.Systematic design of adaptive controllers for feedback linearizable systems[J].IEEETransactionson Automatic Control,1991,36(11):1241-1253

[7]SUN W,GAO H,KAYNAK O.Adaptive backstepping control for active suspension systems with hard constraints[J].IEEE/ASMETransactionson Mechatronics,2013,18(3):1072-1079.

[8]赵海英，邝钰，吴忠强.汽车主动悬架的自适应Backsetpping控制[J].制造业自动化，2013，35(8)：113-117.

[9]BASTURK H I.A backstepping approach for an active suspension system[C].American ControlConference.Boston,IEEE,2016:7579-7584.

[10]YOSHIMURA T.Adaptive backstepping discrete-time control for a full-car active suspension[J].International Journal of Vehicle Autonomous Systems,2017,13(3):221.

[11]RATH J J,VELUVOLU K C,DEFOORT M.Output feedback based sliding mode control of active suspension using backstepping[C].InternationalConference on Control, Engineering & Information Technology.Tlemcen,IEEE,2015:1-6.

[12]周辰雨，余强，张凯.基于滤波技术的非线性Backstepping主动悬架控制[J].长安大学学报(自然科学版)，2017，37(2)：115-126.

[13]LIU B,SAIF M,FAN H.Adaptive fault tolerant control of a half-car active suspension systems subject to random actuatorfailures[J].IEEE/ASMETransactionson Mechatronics,2016,21(6):2847-2857.

[14]陈双.基于电控空气悬架的轿车平顺性和操纵稳定性协调控制研究[D].长春：吉林大学，2012.

[15]LIN J S,KANELLAKOPOULOS I.Nonlinear design of active suspensions[J].IEEE Control Systems,1997,17(3):45-59.