基于二分法-PSO的碰摩转子有限元模型修正

刘 涛，刘 娟

（1.呼和浩特铁路局 包头车辆段，内蒙古 包头 150200；2.中国石油大学（北京）机械与储运工程学院，北京 102249）

旋转机械在我们的生活中起着非常重要的作用，伴随着现代工业的发展，旋转设备向着高精度，高速化和智能化的方向发展，从而导致转子和定子间的间隙越来越小，结构越来越紧密，转子碰摩故障发生得越来越频繁[1]。

转子与定子碰摩是一类非常复杂的动力学问题。采用刚柔耦合的转子有限元模型，研究一个或少数几个参数对碰摩响应行为的影响，为常用的研究路径[2]。如何建立一个精度较高的含有碰摩故障的转子模型，对转子碰摩故障的研究，是很重要的。以模态试验为依据，进行模型修正，可以有效地解决模型精度较低的问题。从1968年Fox和Kapoor首次提出特征向量灵敏度的计算方法开始，基于灵敏度的模型修正方法得到广泛应用[3]。徐张明，高天明和Amar Bouazzouni，Mohammad等都对灵敏度模型修正方法进行了研究，且取得了一定的成果[4–6]。现在应用较为广泛的方法为基于有限元模型的设计参数型修正方法，其优点是物理意义清晰，工程实用性更强。其中，基于灵敏度分析的设计参数型模型修正方法应用最广泛[7]。随着工程需求的日趋提高，人们对模型修正技术的计算精度和计算效率也有了更高的要求。

为了提高刚柔耦合转子模型柔性转轴的精度，以及模型修正技术的计算精度与计算效率。本文基于模态试验数据，将二分法–PSO作为模型修正的优化算法，实现有限元模型修正，从而提高了有限元模型修正的速度与精度，且避免了在SPO迭代寻优过程中陷入局部最优解的问题。基于模型修正理论，利用转子系统模态试验获取的转轴固有频率，以及WorkBench建立的有限元模型，进行模型修正。研究结果表明，修正后的有限元模型精度有了大幅度的提高，可以较为准确地反应试验模型的结构特征。最后利用修正后的模型进行转子碰摩故障动力学特性的研究，考虑转速变化对碰摩故障的影响，通过分析结果可以知道修正后的转子模型可以较为准确地反映试验模型的运行结果。

1 模型修正方法理论

1.1 灵敏度模型修正

以灵敏度为基础的迭代修正法与有限元模型的离散本质一致，只需要修正系统中的某几个单元或节点的参数，就可以使有限元模型迅速收敛于与试验数据良好相关的修正模型，因此备受青睐[8–10]。目标函数是最优的设计性能，它是有关设计变量的函数

其中p代表设计参数向量，{fe}，{fp(p)}分别代表结构动态特性的实验值和分析值；r(p)为残差项；VLB、VUB分别代表结构设计参数变化的上下限；Wf代表结构各个特征量之间的加权矩阵。

灵敏度的计算公式为

则修正公式可以写成

其中S−为灵敏度矩阵S的广义逆，因此只要得到系统的灵敏度矩阵，确定了特征量的变化量就可以通过优化迭代法确定参数的变化量。

1.2 粒子群优化算法

PSO是一种随机搜索全局优化新方法，相较于其他算法，具有实现容易、精度高、收敛快等特点[11]。

对于有N个粒子群Xi（xi1，xi2，…，xid）的速度，位置更新公式为

其中Vi(vi1，vi2，…，vid)为始速度，Pbesti为粒子Xi找到的最优点，Gbest为所有粒子找到的最优点，C1，C2为加速度因子，r1，r2是均值，用以增加粒子的多样性，ω为惯性权。

1.3 二分法–PSO

PSO算法在迭代过程中随机性较强，要达到高精度需要较长时间。为此将二分法引进迭代中，由盲目搜索变成计划搜索。

因此，按照图1中的流程，完成对转子系统的模型修正。

图1 基于二分法–SPO的模型修正总体思路

具体算法：

(1)初始化X，V，Gbest，Pbest；

(2)更新X，V；

(3)给定的搜索区间：

计算函数Fj=f(X1min，X2min，…，Xjmax，…Xnmax)，

其中j=1，2…n；选取最小值Fi=min(F1，F2，…Fn)，即Fi=f(X1min，X2min，…，Ximax)；

(4)按式(5)或者式(6)更新参数X；

(5)判断：设定误差e，若Fi＜e，进行步骤6，若若Fi＞e，返回步骤3；

(6)更新Pbest，Gbest；

(7) 判 断 如 果 iter＞iterMax，或 者 Gbest＞GbestMax，则退出计算，否则返回步骤2。

2 分析模态

2.1 试验模态分析

为了获得试验数据，通过对自由-自由状态下的转子结构进行激振，测量激振力和响应数据，进行数据采集和信号分析，从而获得模态数据[12]。试验时用充气的轮胎垫住转子结构以模拟自由-自由状态。如图3所示。

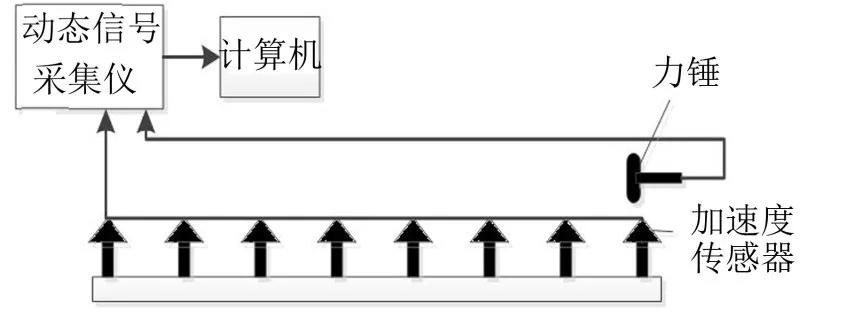
图2 模态试验设计图

图3 转子有限元模型

选择转轴的8个节点作为测点，采用单点激励输入、多点输出方式，对转子系统的每一个测点施加一定的激励，用加速度传感器采集激励力信号，采集节点上的振动响应信号。其中设备包括：转子振动实验台，传感器，力锤，等。根据采集到的激励信号和响应信号，识别出转轴前4阶固有频率，如表1所示。

表1 转轴前4阶固有频率

2.2 计算模态分析

在SolidWorks软件中建立转子系统的三维实体模型，模型构建过程中忽略该结构件中某些局部结构，如圆角、倒角等细节以减少有限元计算时间，提高有限单元的协调性。将适当简化后的三维模型导入ANSYS Workbench进行有限元分析。由于模型中的轴承为滑动轴承。因此，通过弹性阻尼连接方式的Bushing连接进行模拟，由于阻尼较小忽略不计，而轴承刚度通过K值来计算。

边界条件为：在转轴的两端以及中间部分添加圆柱约束，同时，在转轴中安装转子的部分添加应力。网格划分：采用Workbench自动网格划分技术，智能地控制网格大小，使得计算精度不会太低，又可以保证计算速度不会太低。最后进行受力分析，建立有限元模型，同时进行模态分析计算，得到相应的模态参数。转子系统有限元模型如图3所示，图4为转轴前4阶模态的振型图。

3 模型修正结果

参数的选择与试验中灵敏度有很大的关系。首先考虑可能影响有限元模型的几个特征参量：弹性模量E，密度M，质量系数M、C，转轴的截面半径R，转轴的长度L，转轴的支承刚度K。而各个参数对模型特性的影响程度不同，鉴于参数灵敏度是选择优化参数的一个重要指标，表示各参数对模型特性的影响程度。因此，可以通过灵敏度的分析确定需要优化的参量。

图4 转轴前4阶模态特性

如图5所示，各参数在各阶次模态下的灵敏度是不同的。为了提高迭代优化的效率，防止在迭代过程中发生病理现象，在参数选择中，需选择灵敏度较高的参量。质量系数MC与长度L的灵敏度相对于其他参量较小可以忽略不计，转轴的截面半径R，弹性模量E，轴承刚度K灵敏度相对较大，可以选择为待修正的设计参量。同时，密度M的灵敏度虽不是很大，但对计算结果影响较大，因此也作为优化参量。

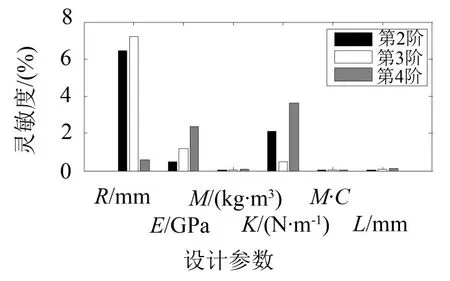
图5 优化参数及其灵敏度分析

在模型修正的过程中，各阶次的固有频率与试验结果间的误差是不断变化的。如图6所示。

这是分别采用PSO算法与二分法–PSO算法对目标函数进行优化迭代的过程。PSO算法与二分法–PSO算法都是伴随着迭代次数的增加，目标函数值不断变小，直到最后趋于稳定。然而PSO算法对目标函数的优化迭代在20次以上误差逐渐稳定且趋于0，而二分法–PSO方法对目标函数的优化迭代在10次左右，误差就逐渐稳定且趋于0。同时，二分法–PSO方法每次迭代计算所用时间比PSO算法每次迭代计算所用时间少。经过简单计算可以看出，改进后的方法迭代计算所用时间少于传统方法所用时间。

由此可以证明采用二分法–PSO算法对目标函数的优化迭代的速度更快。同时得到表2所示的修正前后的设计参数值。

图6 目标函数收敛过程

从表3的结果可以看出，修正前固有频率与试验分析获取的固有频率间的差异相对较大，说明仿真前的模型在反映试验模型的结构特性时，误差相对较大。而修正后的有限元模型的计算结果与试验测试结果更相近，即采用PSO方法与基于二分法–PSO方法进行修正后的结果都比初始模型分析结果的准确度要高，而且基于二分法–PSO方法修正结果的误差比PSO方法修正的误差更小。说明了修正方法及设计参数优化结果的正确性，同时可以表明基于二分法–PSO的修正方法可以得到更高的计算精度。

4 模型应用

图7 转子碰摩试验

以图7所示的试验台为仿真研究的原型，进行转子系统碰摩故障的研究，其中碰撞位置采用塑料块与转子圆盘摩擦模拟碰摩故障。

将修正后的有限元模型导入ADAMS中，构建刚柔偶合的转子模型，然后进行转子系统碰摩故障的动力学仿真研究。由于试验转子的1阶临界转速为5 160 r/min，偏心量为m∙r=2.5×10-4kg∙m，碰摩间隙设置为0.15 mm。在ADAMS中，碰摩故障的研究主要利用IMPACT函数来模拟两个构件之间的碰撞力，IMPACT函数构造的碰撞力由弹性力与阻尼力组成的，由于在试验中，用塑料块与转子圆盘摩擦模拟碰摩故障，因此根据ADAMS推荐，碰摩刚度为1 150 N/m，阻比系数为0.68，渗透深度为0.1，碰撞指数为2。然后添加约束条件，即转子与转轴间的固定副，轴与底座间的旋转副。添加一个恒定转速，大小为9 000(度每秒)，即1 500 r/min来模拟电机的驱动，在转子系统的另一边添加一个负载转矩0，为了降低突变带来的误差，因此使用STEP函数控制，使得速度稳定增加到9 000(度每秒)。

图8为修正前，修正后，实验测量获取的振动频率图。

从图中可以看出，修正后模型的振动频率与试验测量的振动频率都在26 Hz左右，而修正前的振动频率在35 Hz附近，对比试验结果，误差较大，因此可以看出修正后的结果更为接近试验结果。

图10是转速为2 760 r/min时的频谱图与轴心轨迹图，通过图9与图10可以看出，在转速低于临界转速时，存在大于基频的高倍频成分，轴心轨迹有内凹现象，伴随着转速的增长，二倍频增加的速度远大于一倍频增长的速度。

表2 修正前后的模型参数

表3 模型修正前后固有频率与误差的变化情况

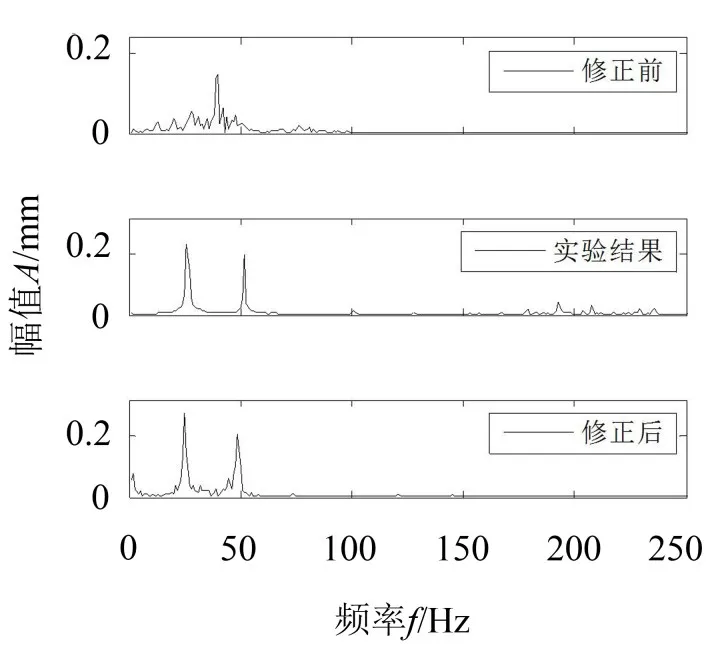
图8 碰摩转子修正前后及实验测量频率图

图9 临界转速以内的仿真结果

图10 临界转速以内的仿真结果

图11为临界转速情况下的振动情况，此时转速在5 160 r/min附近，出现小于一倍频的成分，基频幅值远大于之前，同时，轴心轨迹为多环嵌套；图12中，转速在6 190 r/min附近，是临界转速的1.2倍，因此出现了1X/1.2的低频成分，同时轴心轨迹为多环嵌套。

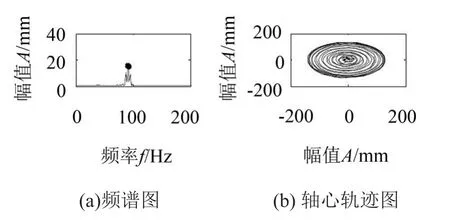
图11 临界转速时仿真结果

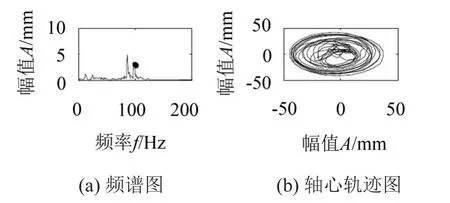
图12 临界转速以外仿真结果

5 结语

为了提高刚柔耦合转子模型柔性转轴的精度，以及模型修正技术的计算精度与计算效率，本文利用模态试验数据，应用二分法–PSO算法实现有限元模型修正的优化计算，从而提高了有限元模型修正的速度与精度，且避免了在SPO迭代寻优过程中陷入局部最优解的问题。对比PSO模型修正的结果与二分法–PSO模型修正的结果，发现基于二分法–PSO的模型修正方法在计算速度，计算精度方面相都有所提高。

将修正后的模型应用在转子碰摩故障的动力学特性研究中，考虑转速变化对转子碰摩动力学特性的影响。研究结果表明，当转速小于临界转速时，伴随着转速的增加二倍频幅值的增长迅速；在临界转速时，振动幅值远大于先前；当转速大于临界转速时，出现低于一倍频的成分。仿真结果与试验结果一致性较高，为实际工程中转子系统的安全稳定运行提供一定的实际参考。

[1]MING ZENG,YU YANG,JINDE ZHENG.Normalized complex Teager energy operator demodulation method and its application to fault diagnosis in a rubbing rotor system[J].Mechanical Systems and Signal Processing,2015(50-51):380-399.

[2]FERNANDO L PONTA,ALEJANDRO D OTERO,LUCAS I LAGO,Effects of rotor deformation in windturbine performance:The dynamic rotor deformation bladeelementmomentum model(DRD-BEM)[J].Renewable Energy,2016(92):157-170.

[3]FOX R L,KAPOOR M P.Rate of change of eigenvectors and eigenvalues[J].AIAA Journal,1968,12(6):2426-2429.

[4]徐张明，高天明，沈荣瀛，等.一种改进的利用频响函数进行有限元模型修正的方法[J].振动与冲击，2002，21(3)：43-45.

[5]ASMA F,BOUAZZOUNI A.Finite element model updating using variable separation[J].European Journal of Mechanics-A/Solids,2007,26(4):728-735.

[6]MOHAMMAD R D,JAVAD V A,SIROUS G,et al.Determination of nonlinear behavior of a ball joint system by model updating[J].Journal of Constructional Steel Research,2012,71:52-62.

[7]GUILLAUME ROSENZVEIG,FRANÇOIS LOUF,A FE model updating method for the simulation of the assembly process of large and lightweight aeronautical structures[J].Finite Elements in Analysis and Design,2016(111):56-63.

[8]BAIYONG GOU,WEIJIE ZHANG,QIUHAI LU.A successive selection method for finite element model updating[J].Mechanical Systems and Signal Processing,2016(70-71):320-333.

[9]NEHETE D V,MODAK S V,GUPTA K.Coupled vibroacoustic modelupdating using frequency response functions[J].Mechanical Systems and Signal Processing,2016(70-71):308-319.

[10]NYSSEN F,GOLINVAL J C.Identification of mistuning and model updating of an academic blisk based on geometry and vibration measurements[J].Mechanical Systems and Signal Processing,2016(68-69):252-264.

[11]ZHANG C,SUN J.An alternate two phases particle swarm optimization algorithm for flow shop scheduling problem[J].Expert Systems with Applications,2009,36(3):5162-5167.

[12]庆光蔚.基于复模态和频响修正方法的磁轴承-转子系统参数识别[D].南京：南京航空航天大学，2010.