共振式消声器气流再生噪声分析
2018-03-03王岩松魏民祥
朱 福,郭 辉,,,王岩松,魏民祥,吴 江
(1.上海工程技术大学 汽车工程学院,上海 201620;2.南京航空航天大学 能源与动力学院,南京 210016;3.宁波思明汽车科技股份有限公司,浙江 宁波 315171)
汽车排气消声器在实际使用中,因受到流速和温度等因素的影响,导致消声性能与理论值有一定差异[1],最近十几年国内外学者开始关注消声器的多场耦合分析。邓兆祥等研究了流场和声场随穿孔管式消声单元结构参数变化的规律[2],赵海军等通过实验得出了扩张腔结构参数对气流噪声声功率级的影响[3]。为研究传递损失和气流噪声与流场之间的关系,康钟绪等和方智等通过数值模拟和实验结合的方法提出随着气流马赫数增加,消声频带向高频段延伸[4–5]。Emmet和Keith利用实验验证了在一定流速范围内气流噪声声压级在流速最大时有最高值[6]。温度场对消声性能也具有一定影响,税永波利用数值模拟方法提了出在高温条件下,扩张腔式消声器高频消声效果增强且传递损失曲线的两个拱形消声峰峰值间的频率间距增大[7]。Nishant K.Singh和Philip A.Rubini提出在考虑气流的扩张腔式消声器的传递损失预测方面,大涡模拟模型比雷诺时均方程模型具有明显优势[8]。上述研究对象皆为简化的典型消声单元,对于实际使用的复杂消声器难以建立准确的数学模型,而三维流体计算可以对多场耦合的气流再生噪声进行准确模拟。
本文以某车用共振式排气消声器为研究对象,利用大涡模拟(LES,Large Eddy Simulation)和声类比(AA,Acoustic Analogy)方法,研究流场、声场和温度场耦合下的气流再生噪声,分析气流再生噪声频谱特性及其随流速和温度的变化特征。
1 LES与AA方法
1.1 大涡模拟
LES湍流模型兼具计算精度高和计算量小的优点,在预测消声器腔内气流噪声方面相对于其他湍流模型具有明显优势[9]。大涡模拟直接对大尺度涡团求解[10],利用亚格子模型对小尺度涡团进行模拟和求解。LES的控制方程如式(1)和式(2)
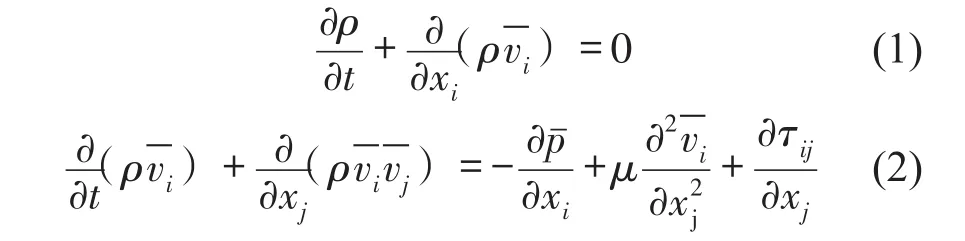
1.2 声类比法
LES方法和AA方法结合,从不同的角度对连续性方程和N-S方程推导[11],把气动噪声的求解分解成了近场和远场两个部分,而声类比中的FW-H方法在预测远场噪声上具有较高的精度[12]。Williams[13]于上世纪60年代提出了气动噪声的FWH方程,可用于远场部分的气动噪声求解。FW-H方程如式(3)
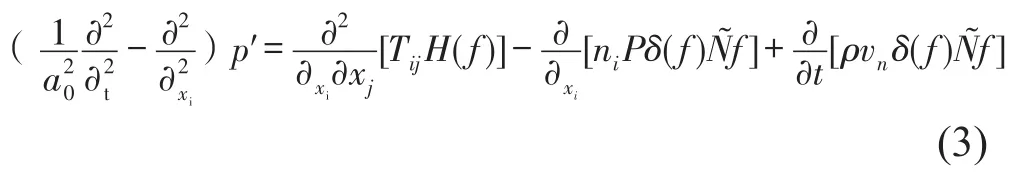
式中a0为声速;p′为声压;ni为表面法向量;vn为法向速度;Tij为Lighthill张量。
通过对方程(3)的结果进行傅里叶变换,即可把时域解变换为频域解,从而得出气流噪声频谱数据。
2 消声器理论模型及验证
2.1 物理模型
消声器的物理模型如图1所示。其中管件分为进气管、内排气管、上排气管和下排气管,进气管前段均匀分布12个直径3 mm的小孔,上下排气管前段均布20个直径为3.5 mm的小孔,中段均布120个直径3.5 mm的小孔;板件分为穿孔板和隔板,厚度均为1.2 mm,穿孔板上分布有160个直径5 mm的小孔。消声器腔体被隔板C分为腔体A和腔体B,腔A是带有进气管和穿孔板的共振腔,腔B为带有内排气管的共振腔。在下排气管出口末端设定近场声压级监测点,在距离下排气管末端端口0.5 m处设定远场声压级监测点,如图1示。
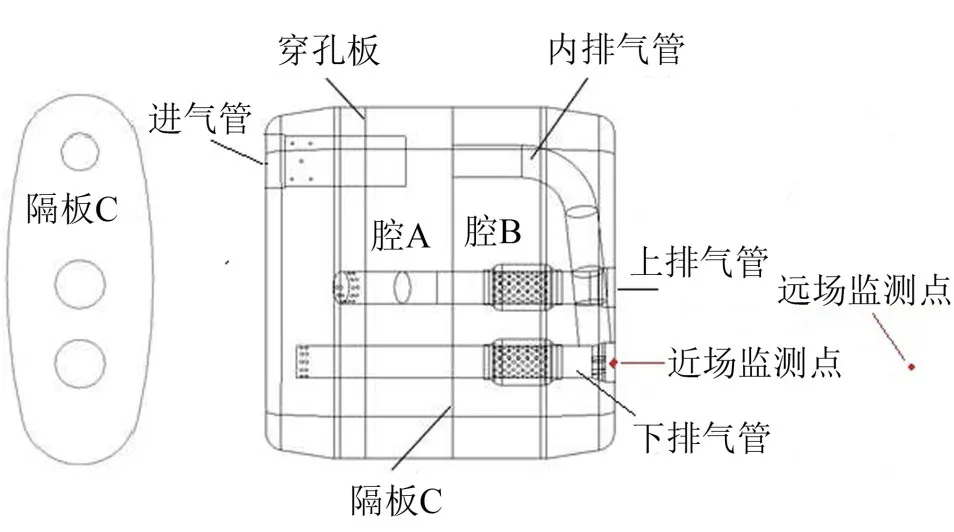
图1 物理模型
2.2 有限体积模型
将消声器的流体区域提取出来,导入流体有限体积软件star-ccm+中进行网格划分。多面体网格具有在同等精度下运行效率更高的特点,因此采用多面体网格。为兼顾计算精度和计算量,基础网格尺寸为5 mm,在小孔以及形变处应用更小尺寸的网格进行局部加密,网格总数约60万,网格模型见图2。

图2 网格模型
设定入口为速度入口,出口为压力出口,其余壁面设置为wall。稳态采用可实现的k-ε模型以及curle和proudman宽带噪声源模型,迭代次数1 000步;瞬态近场采用大涡模拟湍流模型,远场采用FWH模型,时间步设置为2.5×10-5秒,此时隐式求解器处于稳定且节省计算量,离散阶数为2阶,迭代时间为0.12秒。
2.3 实验台搭建
在半消声室内搭建气流再生噪声测试实验台,该系统主要由三个部分组成:气流产生系统、信号采集系统和消声器。其中气流产生系统由风机、消声箱、连接管组成;信号采集系统由两个麦克风、数据采集系统和信号采集与处理软件组成。图3为气流再生噪声测试实验简图。
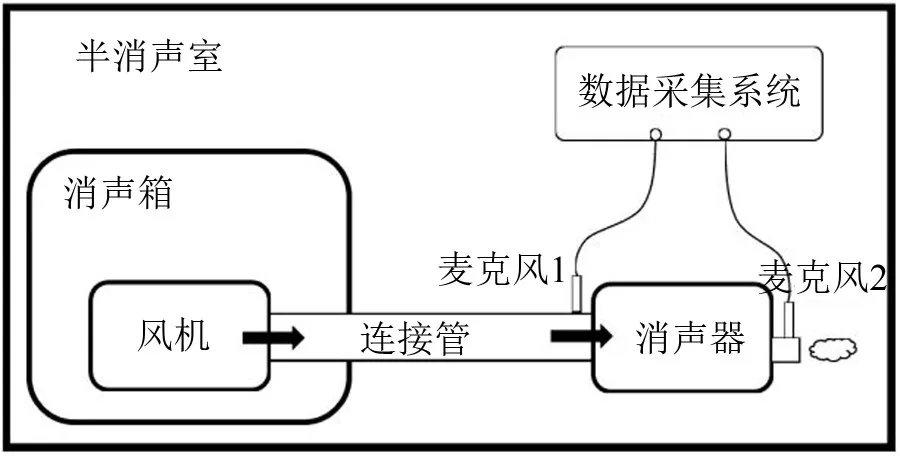
图3 气流再生噪声实验示意图
图4为实验现场图,风机位于自制消声箱内,箱内壁面贴有消音棉,气流通过连接管从风机进入消声器进气管。麦克风1和2分别位于消声器进气管入口端和下排气管出口端。连接管长2 m,数据采集器为LMS SCM05,风机功率300 W。

图4 实验现场图
2.4 仿真与实验对比分析
图5是消声器进口流速10 m/s,温度300 K工况下进气管入口处声压级仿真与实验对比,监测点位于图3麦克风1。仿真结果在300 Hz以下的低频段高于实验结果5 dB~10 dB,在300 Hz以上的中高频段与实验吻合较好。

图5 进气端声压级仿真与实验对比
图6是出口近场监测点声压级仿真与实验对比,监测点位于图3麦克风2。300 Hz以下的低频段仿真结果高于实验结果5 dB~13 dB,300 Hz以上的中高频段仿真结果高于实验结果2 dB~8 dB。
仿真与实验所得数值大体趋势一致,整体吻合较好,但多数情况下仿真数值略高于实验数值,导致这一现象的主要原因是:

图6 出口端声压级仿真与实验对比
(1)仿真计算是在近乎理想的边界条件下进行的,而实验中麦克风及支架需伸入下排气管,带来一定的排气阻力,使实验数值低于仿真数值。
(2)建立三维模型时,因为孔的排布参数不全,所以仿真数模与实体模型并不完全一致。
虽然仿真与实验数值存在少许出入,但总体吻合良好,验证了仿真计算的有效性,可用于消声器气流再生噪声研究。下一步需计算分析流场和声场分布特征以及不同流速和温度对气流再生噪声的影响规律。
3 结果分析
3.1 流场和声场云图分布分析
图7是消声器模型CFD计算结果,图中(a)(b)(c)(d)分别显示了进口流速为60 m/s、温度为900 K工况下的速度场、偶极子噪声源、四极子噪声源和湍动能的分布云图。其中(a)(c)(d)为消声器中间对称截面,(b)为消声器壳体内壁面。从图7(a)可以看出,流场速度数值较大的区域主要分布在进气管末端、穿孔板和上下排气管。图7(b)表明,偶极子噪声源主要分布在腔A的壳体内壁面,噪声值较大区域为进气管末端附近的内壁面。从图7(c)和(d)可以看出,四极子噪声源和湍动能主要分布在进气管末端、穿孔板和上下排气管处,最大值出现在下排气管的入口处。这是由于消声器在进气管末端、穿孔板和上下排气管处的结构突变处流体质点运动方向发生剧烈变化,导致了流体剪切层的不稳定[14],产生了较大的流速、湍动能、偶极子噪声源和四极子噪声源。
从图7可以看出,速度场、偶极子噪声源、四极子噪声源和湍动能云图在分布上相互对应,具有一致性。这种一致性是由于湍动能、偶极子噪声源和四极子噪声源声功率分别与流体流速的平方、6次方和8次方成正比[15–16]。
图8为消声器中间对称截面湍动能云图,(a)为进口速度50 m/s、温度300 K工况;(b)为进口速度60 m/s、温度400 K工况;(c)为进口速度70 m/s、温度500 K工况。可以看出虽然三种工况的进口流速和温度均不相同,但具有相似的湍动能云图分布特征。图9为以上三种工况的四极子噪声源云图,可以看出不同工况的四极子噪声源云图分布特征较为相似,受进口流速和温度的影响较小。
从图8和图9可以看出,流场和声场在不同工况下具有相似的云图分布特征,进口流速和温度对云图分布特征的影响较小。不同工况下的云图差异主要体现在数值幅度上,因此还需要进一步探讨流场和温度场对气流噪声声压级数值上的影响。
3.2 流场对气流噪声的影响分析

图7 流场和声场云图

图8 湍动能云图

图9 四极子噪声源云图
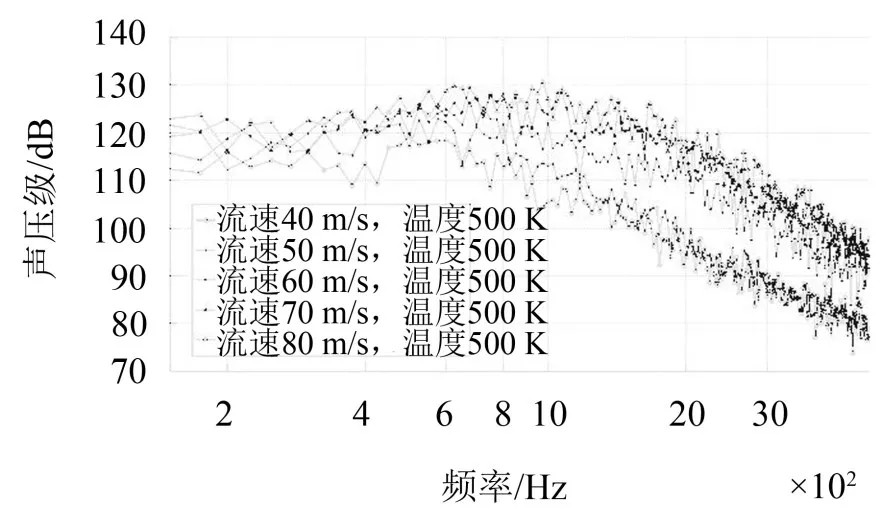
图10 不同流速下近场气流噪声频谱图
图10显示的是近场监测点气流噪声声压级频谱图,近场监测点位于图1中下排气管出口端。5个工况的进口流速分别为 40 m/s、50 m/s、60 m/s、70 m/s、80 m/s,进出口温度均为500 K。
从图5可以看出气流噪声以3 000 Hz以下为主,在5 00 Hz至1 000 Hz之间有声压级峰值,1 000 Hz以上声压级开始衰减,不同工况具有相似的声压级变化趋势。
图11对近场声压级频谱图的800 Hz至2 000 Hz频率段进行了局部放大,可以看出声压级从高到低的曲线依次为进口流速80 m/s、70 m/s、60 m/s、50 m/s、40 m/s工况下的声压级曲线。

图11 不同流速的近场气流噪声频谱局部图
表1显示的是声压级峰值大小,结合图10和图11可以看出随着气流速度增大,声压级大小也随之依次增大。

表1 不同流速下近场气流噪声峰值
图12显示的是距离排气管末端端口0.5 m处的远场监测点声压级频谱图,噪声以200 Hz至3 000 Hz为主,峰值出现在500 Hz至1 200 Hz之间,声压级曲线从高到低依次为进口流速80 m/s、70 m/s、60 m/s、50 m/s、40 m/s工况的曲线。
从表2可以看出远场噪声声压级峰值随着气流速度的增大而增大,与表1和图10显示的近场声压级随进口流速变化的规律相吻合。

图12 不同流速下远场气流噪声频谱图

表2 不同流速下远场气流噪声峰值
由于四极子噪声源声功率级与流速的8次方成正比[15],且流速增大导致气流质量流量增大,气流与物理结构突变的地方产生较大冲击,流体质点运动加剧,导致气流噪声声压级随着气流进口速度的增大而增大。
3.3 温度场对气流噪声的影响分析
图13显示的是近场气流噪声声压级频谱图,近场监测点位置见图1。五个工况的热力学温度分别为500 K、600 K、700 K、800 K、900 K,进口流速均为70 m/s。可以看出气流噪声以3 000 Hz以下为主,峰值出现在600 Hz至1 000 Hz,1 000 Hz以上开始衰减。
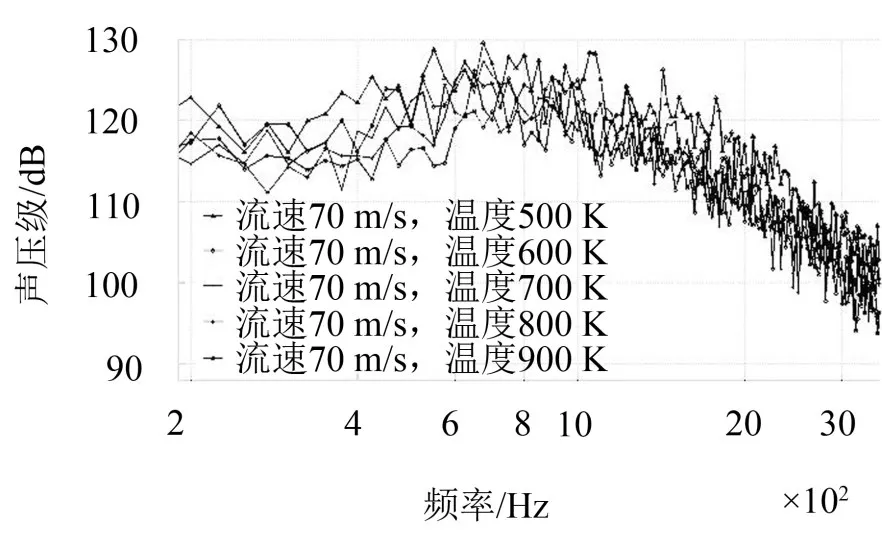
图13 不同温度的气流近场噪声频谱图
图14为气流近场噪声频谱曲线400 Hz至1 000 Hz频率段的局部放大图,从曲线总体分布可以看出声压级从高到低的曲线依次为温度500 K、600 K、700 K、800 K、900 K工况的曲线。
从表3可以看出声压级峰值随着温度的升高而降低,结合图13和图14可以看出随着温度的升高,声压级整体随之减小。
图15显示的是距离排气管末端端口0.5 m处的远场监测点声压级大小,远场噪声峰值大小相对接近,但从频谱特性曲线的300 Hz至600 Hz频率段可以看出,温度500 K的声压级曲线最高,温度900 K的声压级曲线最低,温度600 K、700 K和800 K的声压级曲线处于500 K和900 K的声压级曲线之间且依次降低,与图13和表3显示的近场声压级随温度变化的规律相吻合。

图14 不同温度的近场气流噪声频谱局部图

表3 下不同温度下近场气流噪声峰值

图15 不同温度下远场气流噪声频谱图
根据理想气体状态方程,进口流速不变,当温度升高时,气体体积膨胀,密度减小。声传播介质的密度越小时,声传播速度越小,且质量流量减小,由此导致气流再生噪声随温度的升高而减小。
5 结语
本文以共振式消声器为研究对象,通过数值模拟的方法分析了多场耦合下的气流再生噪声,研究表明:
(1)利用LES和AA结合的方法,研究了多场耦合下的共振式消声器气流再生噪声,仿真结果表明气流再生噪声以3 000 Hz以下为主。
(2)同一工况的速度场、湍动能、偶极子噪声源和四极子噪声源之间的云图分布特征相互对应,具有一致性;不同工况下的流场和声场具有相似的云图分布特征。
(3)温度一定时消声器气流再生噪声随进口流速的增大而增大,进口流速一定时气流再生噪声随温度的增大而减小。但速度和温度的数值大小对频谱特性的影响较小。
[1]刘丽萍,肖福明.扩张腔式消声器气流噪声的试验研究[J].机械工程学报,2002,38(1):98-100.
[2]邓兆祥,赵海军,赵世举,等.穿孔管消声器单元气流再生噪声产生机理[J].内燃机学报,2009(5):21-25.
[3]赵海军,邓兆祥,潘甫生.共振式消声器气流再生噪声发生机理研究[J].内燃机工程,2010(31):74-77.
[4]康钟绪,郑四发,连小珉,等.穿孔管消声器有流声学性能的数值预测[J].内燃机工程,2011(5):7-10.
[5]方智,季振林.均匀流直通穿孔消声器的声学特性分析[J].声学学报,2015,40(3):404-412.
[6]EMMET JENGLISH,KEITH R HOLLAND.Aeroacoustic sound generation in simple expansion chambers[J].Acoustical Society of America,2010,128:2589-2595.
[7]税永波,徐小程,曹志良.基于多场耦合的汽车排气消声器声学性能研究[J].制造业自动化,2015(4):67-69.
[8]NISHANT K SINGH,PHILIP A RUBINI.Large eddy simulation of acoustic pulse propagation and turbulent flowinteraction in expansion mufflers[J].Applied Acoustics,2015,98:6-19.
[9]吕景伟,季振林.变截面内管道内流噪声预报与实验测量[J].噪声与振动控制,2011,31(1):166-169.
[10]张兆顺,崔桂香,许春晓.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社,2008:57-60.
[11]但佳壁,郑四发.基于大涡模拟和声比拟的喷射流噪声时域预测方法[J].振动工程学报,2016,29(3):504-510.
[12]ALIREZA BOZORGIA.A two-dimensional solution of the FW-H equation for rectilinear motion of sources[J].Journal of Sound and Vibration,2017,388:216-229.
[13]WILLIAMS J E F,HAWKINGS D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Philosophical Transactions of the Royal Society of London,Mathematical and Physical Sciences,1969,264(1151):321-342.
[14]ASHCROFT G B,TAKEDA K,ZHANG X.A numerical investigation of the noise radiated by a turbulent flow over a cavity[J].Journal of Sound and Vibration,2003,265:43-60.
[15]LIGHTHILL M J.On sound generated aerodynamically[J].Proceedings of the Royal Society of London,1952,211(1107):564-587.
[16]PAPAXANTHOS.Pressure-based integral formulations of lighthill-curle's analogy for internal aeroacoustics at low mach numbers[J].Journal of Sound and Vibration,2017,393:176-186.
