卡车驱动桥壳体机械扩胀成形工艺分析及实验研究

罗建国 李 攀

华北科技学院机电工程学院，廊坊，065201

0 引言

驱动桥壳是一种大尺寸的复杂金属管类零件， 被用作驱动桥传动系统的支撑体，为传动系统的正常运转提供保证[1],因此，驱动桥壳是车辆底盘驱动桥总成的关键承力零件。另外，在卡车驱动桥的诸多组合结构中，驱动桥壳的质量最大、形状也最复杂，这些特点致使该类零件的生产制造具有较大的难度[2-3]。目前,车桥制造行业生产大中型的车辆驱动桥壳时，主要采用铸造或冲压焊接的生产工艺。铸造桥壳虽然强度和刚度较大，但铸造工艺不易控制且能量和材料消耗较多；而冲压焊接桥壳的质量虽有所减轻，但冲压焊接工艺流程多，产品在长期使用后会出现漏油和局部断裂等缺陷[4-5]。为满足当前车辆制造在强度、轻量化和成本控制等方面的强烈需求，驱动桥壳体的整体结构设计应运而生，而开发与之配套的新型成形技术则是实现汽车轻量化和保证其安全使用性的重要手段，因此，整体式驱动桥壳体成形工艺的开发亦逐渐成为车辆制造行业竞相研究的热点[6-8]。

国内外关于整体式驱动桥壳体成形技术的研究主要集中于以无缝钢管为原料的中部扩胀成形方面,目前虽已提出了较多的成形方法，但尚未形成一种成熟的整体式驱动桥壳体成形工艺，而在厚壁管的驱动桥壳体成形方面，机械扩胀成形技术已成为研究重点[9-10]。20世纪80年代，美国和法国率先采用机械扩胀技术进行了汽车驱动桥壳体的胀形成形[11]。国内在上世纪末引入法国的机械热扩胀成形工艺后，国内学者以热胀形技术为基础展开了相关研究[12]，机械扩胀技术才得以迅速发展。赵宇峰[13]对有芯胀形和无芯胀形的成形过程进行了数值模拟，并对比了预制孔的形状尺寸因素对管坯成形性的影响。韩英淳等[14]总结出预制孔与凸模形状的匹配问题，基于轴向进给量和整形特征，提出了过胀反整形的校形方法并讨论了胀形系数对桥包成形质量的影响。但是，国内对驱动桥壳体机械热扩胀成形技术的研究多处于理论研究和数值模拟阶段，且缺乏足够的实验验证。

本文结合中型卡车驱动桥壳体的结构特点，提出一种在带有轴向辅助推力的条件下，使用无缝钢管并采用机械扩胀成形技术成形驱动桥壳体的新型成形工艺。研究过程中推导了该工艺下管坯极限扩胀成形系数的解析式，研究了成形过程各方向上力参量的匹配关系对扩胀成形系数的影响规律。以某中型卡车驱动桥壳体为研究对象，通过数值模拟结合工艺实验，对所提出的成形工艺进行了分析和验证。

1 驱动桥壳体机械扩胀成形工艺

以截面为方形的无缝钢管为工件坯料，利用本文所提出的成形工艺制造驱动桥壳,详细的工艺流程如图1所示。主要步骤为：①开预制孔(在管坯中部相互平行的两个侧面切割具有一定形状和尺寸要求的预制通孔)；②尖劈预成形(利用一定形状的尖劈渐进穿过两个预制孔，使预制孔在垂直于钢管轴向方向上的尺寸变大，从而形成可以容纳扩胀芯的空间)；③径向机械胀形(利用制动尖劈驱使两个背对的扩胀芯在垂直轴线的半径方向上做反向运动，从而将预制孔扩胀至琵琶包的最大径向尺寸,径向胀形的同时，需要在钢管轴线方向上对桥壳体两个端面施加等值反向的辅助推力)；④轴向整形(利用整形芯模消除琵琶包外壁和胀形凹模内壁之间的缝隙，完成桥壳体的成形)。

图1 驱动桥壳体机械胀形主要工艺流程图Fig.1 Main process flow chart of mechanical bulging for drive axle housing

2 无缝钢管机械扩胀成形系数研究

管坯极限扩胀成形系数，表征了无缝钢管的胀形区域在相应的加载工况和外部环境下所能被胀大的极限程度，定义为K=dmax/d0,其中dmax表示胀形后扩胀区的径向尺寸，d0表示胀形前扩胀区的径向尺寸。如果扩胀成形系数过大，使扩胀区的变形超过了管坯材料所允许的胀形极限，则桥壳的胀形区域就会发生破裂，因此，管坯极限扩胀成形系数对于确定驱动桥壳在扩胀芯从内向外扩胀方式下的成形规程十分重要。针对壁厚较大的管坯，钢管中部需加热至高于材料的再结晶温度才能进行扩胀，文献[10]中表明了金属管材在高于金属再结晶温度条件下的极限胀形比不得超过2.5。对于壁厚或胀形程度不大的桥壳体，选择常温下或将包含预制孔的管段加热至低于材料再结晶温度即可满足扩胀的要求。另外，加热温度在低于金属再结晶温度下，扩胀区金属质点之间抻拉效应较大，变形过程中壁厚变化受压应力的影响较小，壁厚的变化趋势更加符合桥包在工作状态下的受力分布。而关于管坯在低于材料再结晶温度条件下进行机械扩胀的极限成形系数的确定，国内外学者尚未有明确的研究成果。本文提出的工艺，加热区温度低于金属再结晶温度且带有轴向辅助推力，该工艺决定了极限胀形系数应在特定范围取值。

在钢管中间部位变形区的内壁上截取单元体作为研究对象。由于管坯中部被预制孔隔断，中部的质点在垂直胀形面方向的应力可忽略不计，此时单元体所受的应力为环向应力σθ和径向应力σp，可近似看作平面应力状态。多数工程常用金属在低于其再结晶温度时会发生大变形，都会产生加工硬化,管坯进行径向扩胀时，材料的真实应力-应变曲线可用幂指数形式表达如下：

σs=BEn

(1)

式中，σs为材料的屈服应力;E为对数应变;B为强度系数；n为硬化指数。

根据抛物线型真实σ-ε曲线的经验方程可得到强度系数B和硬化指数n，即

于是有

(2)式中，δu为金属材料的拉伸率;Yb、Eb分别为应变曲线上失稳点的等效应力和对数应变;σb为材料的抗拉强度。

假设塑性变形过程中体积不变，令ξ=ερ/εθ，其中，ερ为质点径向的正应变;εθ为质点环向的正应变。导入等效应变方程，可得到如下表达式：

(3)

式中,Eθ为质点环向的对数应变。

设胀形后桥壳琵琶包的外径为Dt，胀形前的外径为Dt-1，对于最大胀形部位的质点有Eθ=ln(Dt/Dt-1)。假定在径向机械胀形时，桥壳最大胀形处质点的塑性应变和应力偏量成比例，则

可推导得到

(4)

将式(4)代入式(2)，得

即

由于σθ≤Yb，则极限胀形系数K可表示为

(5)

3 机械扩胀成形中力的匹配

根据工艺的成形技术原则，桥壳体扩胀成形发生于钢管中部包含预制孔的管段，而钢管两端的直臂段不发生塑性变形，因此钢管两端所受的压应力不得超过常温下金属材料的真实屈服应力。若根据需要，胀形前将胀形区加热至低于金属再结晶温度的某一温度，再加上金属在变形过程中产生的变形热，因此不管是否加热，在成形过程中，管坯中部金属的温度总是高于不参与扩胀的直臂部分。由于温度的作用，扩胀区金属的屈服应力比直臂部分金属的屈服应力要小得多。由此可以得出，扩胀时桥壳两端辅助推力的取值条件，即琵琶包最大胀形部位垂直于轴向的截面上，由辅助推力所产生的压应力的绝对值不得大于在该温度下金属材料的真实屈服应力。

那么，设辅助推力为Fp，管坯扩胀区在低于金属再结晶温度以下时，最大胀形处质点的最大环向应力σθ可表示为

σθ=Fp/(2S)+σs

(6)

式中，S为最大胀形处单个横断面的面积(在扩胀过程中近似不变)。

设扩胀芯模具胀形面的面积为S0，单侧胀形载荷为Fb，则在胀形过程中，径向应力σρ可表示为

σρ=Fb/S0

(7)

在径向机械扩胀成形过程中，胀形区各个质点的应力应变状态是不同的。在成形阶段的绝大多数时间里，琵琶包最大胀形部位的应力和应变状态约束着扩胀变形的极限胀形量。因此，为调整辅助推力和胀形力，可通过控制最大胀形处质点的应力应变状态，从而达到调节极限胀形系数的目的。图2和图3所示分别为在低于金属再结晶温度时进行扩胀，σρ/σθ和ερ/εθ变化对极限扩胀成形系数的影响规律。由图2和图3可以看出，

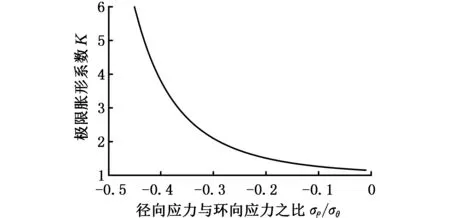
图2 σρ/σθ对极限胀形系数的影响Fig.2 The influence of σρ/σθ on the limit bulging coefficient

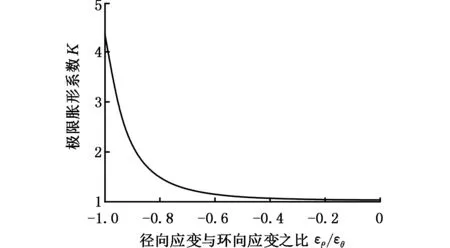
图3 ερ/εθ对极限胀形系数的影响Fig.3 The influence of ερ/εθ on the limit bulging coefficient

在胀形区金属未被拉裂的情况下，径向扩胀应力与环向应力之比的绝对值和径向应变与环向应变之比的绝对值越大，径向极限扩胀成形系数就越高。

4 驱动桥壳体机械扩胀成形数值模拟

本文利用所提出的工艺，对使用无缝钢管在常温下扩胀某5 t卡车驱动桥壳体琵琶包的主要成形过程进行了数值模拟。该桥壳体的形状尺寸如图4所示。

图4 驱动桥壳体示意图Fig.4 The diagrammatic sketch of drive axle housing body

有限元模拟中采用桥壳体的1/2模型，如图5所示。钢管材料为20Mn2,截面尺寸规格为100 mm×100 mm×8 mm。预胀形尖劈下行速率为35 mm/s，扩胀芯的径向运动速率为14.5 mm/s，模具和管坯的摩擦因数为0.12。对流热交换系数为0.02 N/(s·mm·K)，坯料与模具间的传热系数为5 W/(m2·K)。

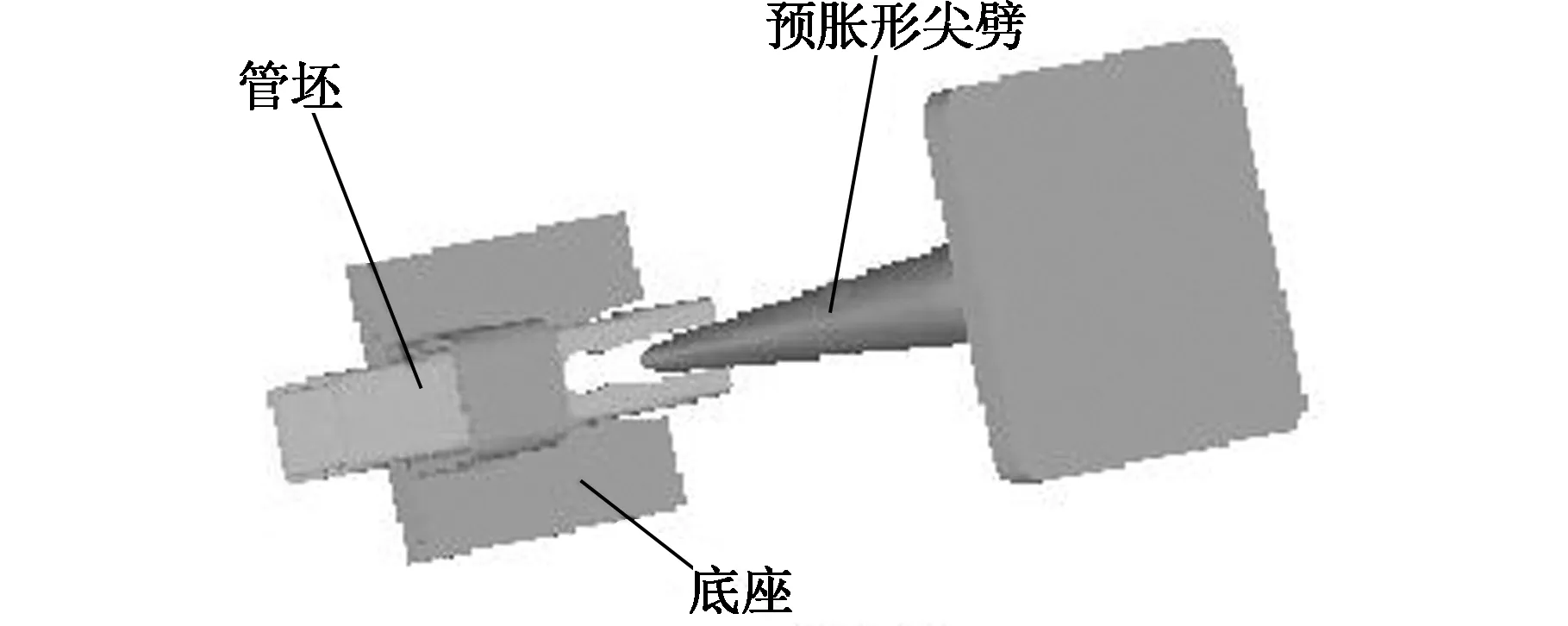
(a)尖劈预胀形模型

(b)径向扩胀成形模型图5 驱动桥壳体成形过程有限元模型Fig.5 The finite element model for forming process of drive axle housing body

为了方便对比，在预胀形之后，分别对无轴向辅助推力和有辅助推力的情况进行模拟。工艺实验中，压力机能够分配用来驱动扩胀芯的推力为41 t，扩胀芯胀形面的面积约为17 966 mm2,最大胀形处单个截面的面积约为1 001 mm2。若侧向辅助推力为112 t，运用所推导的极限扩胀成形理论，求得该条件下方管的极限胀形系数约为1.983，取其90%，则径向扩胀时的成形系数为1.785。预胀形后桥壳体的最大径向尺寸为170 mm，胀形系数1.785在理论上满足一次性成形的要求，故不需要进行分道次扩胀。

无辅助推力条件下直接进行扩胀后，桥壳体的应力应变分布如图6所示。由图6可以看出，桥壳变形过程中等效应力和等效应变在琵琶孔两侧与直臂段结合处发生弯曲的部位最为集中，该部位在扩胀过程中的最大等效应力可达到795 MPa,超过常温下20Mn2材料的抗拉强度785 MPa，理论上该部位已经出现了裂纹。图7所示为有辅助推力条件下扩胀后应力和应变分布。由图7可以看出，其最大等效应力为758 MPa,小于材料的抗拉强度，理论上未发生破坏。胀形后，应力集中区的壁厚减薄程度较大，是最容易发生拉裂的部位。模拟结果证明在以扩胀芯为主导径向成形的情况下，变形区受拉应力的影响较大，轴向辅助载荷不能改变金属的流动方向，但对缓解预制孔两侧拐角部位应力集中和改善产品的成形性具有重要作用。

(a)等效应力 (b)等效应变图6 无轴向推力扩胀后应力和应变分布Fig.6 The stress and strain distribution after expansion without axial thrust

(a)等效应力 (b)等效应变图7 有轴向推力扩胀后应力和应变分布Fig.7 The stress and strain distribution after expansion with axial thrust

5 驱动桥壳体机械扩胀成形实验

为验证所提出桥壳体机械胀形工艺的可行性，选择合适的无缝钢管进行5 t卡车驱动桥壳体的机械扩胀成形实验。需强调的是，在径向扩胀成形实验中，扩胀芯的运动是在制动尖劈的驱使下进行的。扩胀芯的后侧带有凹槽可作为限制制动尖劈运动的导轨，制动尖劈下行，驱动两个扩胀芯反向运动，从而使得胀形区发生形变。实验在1 000 kN/4 000 kN×2多向液压机上进行，轴向辅助推力由液压机两侧的油缸提供，实验工装设备如图8所示。无缝钢管的材质、规格及成形工况与数值模拟相同，管坯与模具的接触区域涂抹润滑剂以减小摩擦。

(a)尖劈预胀形工序 (b)径向扩胀成形工序 图8 驱动桥壳机械扩胀成形实验过程Fig.8 The process of mechanical bulging forming experiment for drive axle housing body

未施加轴向辅助推力进行径向机械扩胀后，在胀形区两侧与直臂段结合处发生弯曲的部位产生了破裂,如图9所示，其结果与数值模拟的结果一致。而通过压力机两侧滑块对钢管两侧施加轴向辅助载荷进行径向扩胀后得到的桥壳体没有发生拉裂，琵琶包的径向部分已完全成形(图10)。后续经过轴向整形即可完成桥壳体的成形，充分证明了施加轴向辅助载荷对于防止拉裂缺陷的必要性。

图9 胀裂的桥壳体及其裂纹Fig.9 The cracked drive axle housing body and its crack

图10 扩胀前的管坯和成形桥壳体(未破裂)Fig.10 The tube material and axle housing body (unbroken)

该驱动桥壳的形状是对称分布的，为了研究胀形区域的壁厚分布情况，沿着对称面截取琵琶包的四分之一部分，对未破裂的驱动桥壳体样件上桥包中间截面a-b-c-d路径的壁厚进行实测，图11为中间截面壁厚测量路径的示意图。实际测量壁厚的分布规律如图12所示。

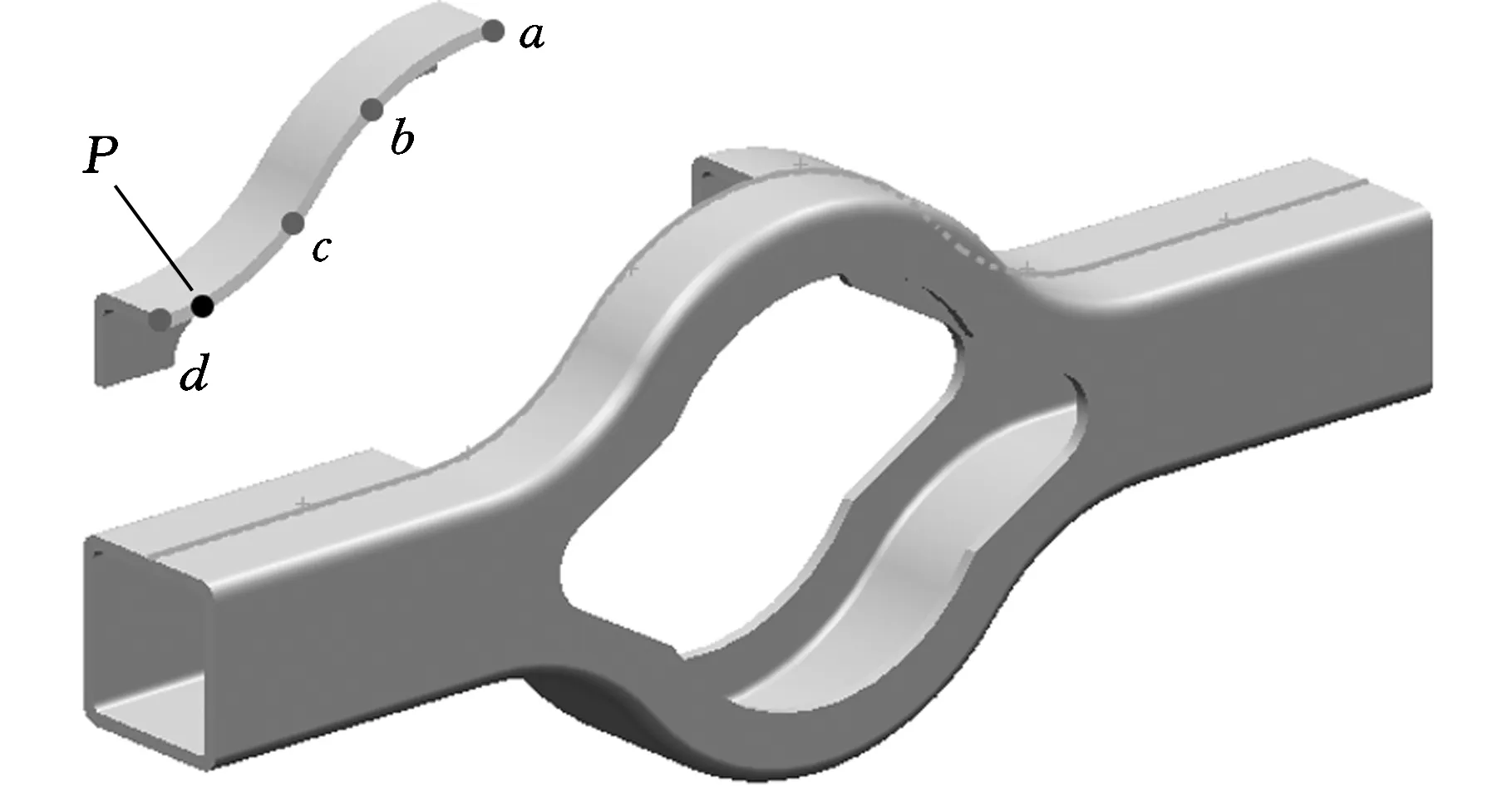
图11 中间截面壁厚测量路径示意图Fig.11 Schematicsketch of the middle cross section and the path of measuring wall thickness

图12 扩胀区实测壁厚与数值模拟壁厚分布对比Fig.12 The wall thickness distribution comparison of practical experiment and numerical simulation

由图12可以看出，扩胀过程中胀形区内壁受到最大压应力的不断变化造成了壁厚逐渐减小，从而出现了少许起伏。试样壁厚最薄位置达6.92 mm，壁厚减薄率为13.5%，具体体现在图11中以a点为起始点的a-b-c-d路径上弧长大约150 mm处，即P点所处位置。本工艺强调的是以扩胀芯的运动为主导的胀形过程，扩胀芯弧面的顶部与胀形区内壁是贴合的，即琵琶包胀形区内壁的顶部受到扩胀芯所施加的压应力作用较大。因此，琵琶包胀形区的顶部和侧端与直臂段连接的拐角部位是成形过程中应力相对集中的区域，导致邻近的金属趋向于这两个部位流动，从而使扩胀区其他部位的金属受到抻拉。随着胀形进程的推进，琵琶包两侧和直臂段结合部位发生弯曲的趋势持续增大，弯曲部位内的质点间会发生一定程度的相互挤压，形成的增厚效应令弯曲区末段的壁厚减薄量较小。胀形区内壁逐步与扩胀芯贴合的部位，由于受到压应力作用，故其减薄趋势逐渐减小；而胀形区内从未与扩胀芯接触，同时又在弯曲变形影响之外的部位，受到抻拉的作用最大。由图12可以看出，胀形区内壁与扩胀芯贴合部位的壁厚从顶部向侧端在总体上接近线性递减，而脱离扩胀芯部位壁厚减小的梯度突然增大，壁厚在最薄点外大幅度增大并恢复至原来的壁厚值。P点位于弯曲区内受弯曲变形增厚效应影响范围的临界区域，因此受拉变薄的程度最大。本实验中，扩胀芯单侧弧面长度为122.5 mm,图12中显示琵琶包切割路径上约150 mm处壁厚减薄程度最大，与前面对壁厚变化的分析相符。另外，实测的壁厚分布规律与数值模拟基本吻合。实验结果验证了本文所提出的驱动桥壳体机械扩胀成形工艺的可行性以及轴向辅助载荷对于改善扩胀区受力状态、防止拉裂缺陷的重要作用。

6 结论

(1)本文提出了适用于中型卡车驱动桥壳体的成形工艺，该工艺的核心工序是在径向机械扩胀的过程中对无缝钢管两端施加轴向载荷。

(2)推导了变形区在低于材料再结晶温度条件下，无缝钢管坯径向机械胀形系数的表达式。揭示了在胀形区金属未被拉裂的情况下，径向极限扩胀成形系数随力的匹配关系调整而变化的规律。给出了径向胀形时轴向辅助载荷的取值范围，即琵琶包最大胀形部位垂直于钢管轴向的截面，由辅助推力所产生的压应力的绝对值不得大于在该温度下金属材料的真实屈服应力。

(3)在以扩胀芯为主导径向胀形的前提下，轴向辅助推力并不能改变扩胀区金属的流动趋势，但能有效地缓解应力集中，因此，施加轴向辅助载荷在径向扩胀过程中是防止胀形区产生拉裂缺陷的必要措施。工艺实验样件胀形区的壁厚分布规律和数值模拟基本吻合，验证了所推导胀形理论的正确性和机械胀形工艺在桥壳体制造领域的可行性。

[1] 王丰元.重型货车驱动桥壳动态特性研究[D].青岛：青岛理工大学,2012. WANG Fengyuan. Research on Dynamic Characteristics of Heavy Truck Driving Axle Housing[D]. Qingdao: Qingdao University of Technology,2012.

[2] 郑娟英.我国重型汽车车桥历史、现状及发展趋势[J].汽车实用技术，2010(2)：19-24. ZHENG Juanying. The History, Present Situation and Development Trend of Heavy-duty Vehicle Axle in China[J]. Automobile Applied Technology,2010(2)：19-24.

[3] WANG Liandong, CUI Yaping, YANG Dongfeng. Study of Bulging-pressing Compound-deforming Automobile Axle Housing with a Common Press[C]// Applied Mechanics and Materials. Ningbo,2012:1972-1977.

[4] 王建东.驱动桥壳生产工艺性探讨[C]// 2009年中国铸造活动周论文集.威海,2009:17-18. WANG Jiandong. Discussion on Manufacturing Process of Drive Axle Housing[C]// The Proceedings of Chinese Casting Activities Week in 2009.Weihai,2009:17-18.

[5] ZHOU Y C, SUN M Z, HE L J. Analysis and Optimization Design on Drive Axle Housing of Light Commercial Vehicle[C]// Advanced Materials Research. Dalian,2013:1314-1317.

[6] ZHANG P M, MA L Q, ZHANG W C. The Finite Element Analysis of Axle Housing[J]. Applied Mechanics and Materials,2015,707:309-312.

[7] ZACHAROF N, TIETGE U, FRANCO V, et al. Type Approval and Real-world CO2and NOx Emissions from EU Light Commercial Vehicles[J]. Energy Policy,2016,97:540-548.

[8] ZHANG Z, ZHANG Y C, LI J, et al. Numerical Simulation on Aerodynamic Characteristics of Heavy-Duty Commercial Vehicle[C]// Advanced Materials Research. Guangzhou, 2012:477-482.

[9] 刘永红.载重车驱动桥壳结构分析及整体挤压成形研究[D].长春：吉林大学，2016. LIU Yonghong. Structural Analysis and Study on Integral Extrusion Forming Process of Axle Housing of Truck[D]. Changchun: Jilin University,2016.

[10] 王源.重型车驱动桥壳整体机械热扩胀整形工艺研究[D].长春：吉林大学，2014. WANG Yuan. Research on Integral Mechanical Thermal Expansion Forming Process of Heavy Duty Vehicle Rear AxleHousing[D]. Changchun: Jilin University,2014.

[11] 薛克敏，李纪龙，李萍,等.汽车桥壳机械式胀形数值模拟及实验[J].塑性工程学报，2013，20(6)：31-34. XUE Kemin, LI Jilong, LI Ping, et al. Numerical Simulation and Experimental Study on the Mechanical Bulging Process of Axle Housing[J]. Journal of Plasticity Engineering, 2013，20(6)：31-34.

[12] 李纪龙.汽车桥壳整体成形数值模拟及实验研究[D].合肥：合肥工业大学，2014. LI Jilong. The Numerical Simulation and Experimental Study of Automobile Axle Housing Bulging Process[D]. Hefei: Hefei University of Technology,2014.

[13] 赵宇峰.汽车后桥壳机械热胀成形有限元模拟研究[D].长春：吉林大学，2010. ZHAO Yufeng. Research on the Finite Element Simulation of the Automobile Rear Axle Housing Mechanical Thermal Expansion[D]. Changchun: Jilin University,2010.

[14] 韩英淳，于多年，赵静宜，等.汽车轻量化的设计与制造新工艺[J].汽车工艺与材料，2003(5)：6-8. HAN Yingchun, YU Duonian, ZHAO Jingyi, et al. Lightweight Design of Automobiles and New Manufacturing Process[J]. Automobile Technology & Material,2003(5)：6-8.