一种3-DOF并联机械手的研制

荣 誉 刘双勇 王洪斌 韩 勇

1.燕山大学控制科学与工程博士后流动站, 秦皇岛,0660042.河北科技师范学院机电工程学院,秦皇岛,0660043.中信戴卡股份有限公司,秦皇岛,066004

0 引言

机械手是人类最早投入工业和科研领域的机器人结构之一[1-2]，金属材料的表面打磨、抛光加工是机械手的重要应用领域[3-5]。铝合金轮毂制造过程中存在大量的打磨、抛光加工工艺过程，目前这些表面的加工还是以人手持打磨工具进行加工的方式为主[6-7]。铝合金轮毂机械打磨、抛光的设备和工艺研究，主要采用两种方式：一种方式是通过常规工业机器人手腕带动打磨电主轴对轮毂进行打磨[8-9]；另一种方式是通过设计专用打磨机床对轮毂进行加工[10-12]。开发一种专用的铝合金轮毂打磨机械手，使其具有承受高负载/高冲击能力、高精度、复杂曲面贴合能力具有重要的意义。

机械手的结构设计和控制系统开发是其最重要的研发内容[13]，其中结构设计起着决定性作用。针对轮毂打磨、抛光过程中的大加工反作用力、大扭矩、高精度要求、高粉尘工况，并联结构比传统工业机器人的串联结构更合适。国内的并联结构机械手的成果主要有：天津大学研发的系列工业机械手[14-15]；上海交通大学研发的串/并联的系列机械手[16-17]；燕山大学研发的欠驱动机械手[18]等。机械手的本体结构设计属于多参数耦合、多目标函数耦合的设计过程，很难实现机械手的各种性能评价指标均取最优值。已有的方法主要包括单目标参数设计法[19]和多目标参数综合设计法[20]。

本文提出一种采用(U+UPS)P+UPS弱耦合并联机构的用于轮毂打磨的3-DOF机械手，并采用矢量回路法对机械手的机构进行了运动学分析与运动灵活性评价，同时，还对机构进行了静力学分析与静力承载性能评价。基于运动灵活性评价指标和静力承载性能评价指标的分布情况，选取了机械手的结构参数，设计出3-DOF并联机械手，并研制出机械手的实验样机。

1 机械手构型

图1为一种支链含闭环的(U+UPS)P+UPS弱耦合并联机构的3-DOF机械手机构简图。机构描述的字母U代表万向副、P代表移动副、S代表球面副。该机构由固定平台、运动平台和中间连接的一个UPS支链及另一个含有闭环的(U+UPS)P支链构成。其中，(U+UPS)P支链的构型方式为：以UP链为主干，且UP链通过万向副与固定平台连接，通过移动副伸缩杆末端与运动平台垂直固接，闭环部分的UPS链一端通过万向副与固定平台连接，另一端的球面副通过中间连接杆与主干部分UP链的移动副套筒固接。不含闭环的UPS支链一端通过万向副与固定平台连接，另一端通过球面副与运动平台连接。为了便于设计制造，将3个移动副选取为驱动运动副。

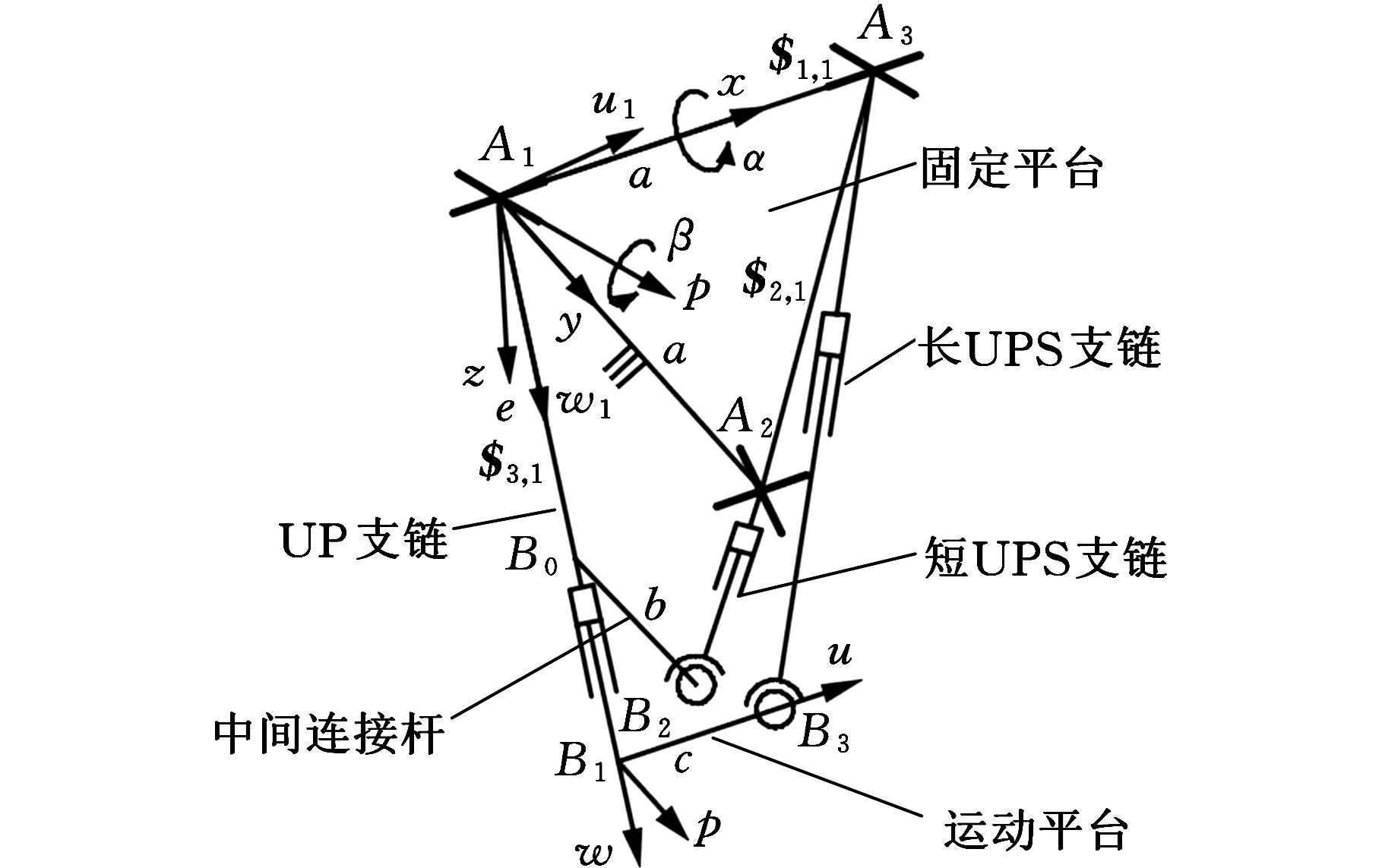
1.固定平台 2.长UPS支链 3.短UPS支链 4.运动平台 5.中间连接杆 6.UPF支链图1 (U+UPS)P+UPS机构简图Fig.1 Schematic diagram of (U+UPS)P+UPS

用螺旋理论进行自由度分析可知[21]，该机构是具有2个转动、1个平移的三自由度机构，其运动平台具有1个约束力偶和2个约束力。为了实现机构各支链间运动的解耦性，这里采用文献[22]的转动解耦性优化方法对机构进行转动解耦运动副布局，使与固定平台连接的3个万向副的位置呈等腰直角三角形布局。其中，(U+UPS)P支链的主干部分UP链的万向副在直角顶点处，且主干UP链万向副和不含闭环的UPS支链万向副靠近固定平台的转动轴线共线；(U+UPS)P支链的闭环部分UPS链的万向副靠近固定平台的转动轴线与上述轴线平行。通过这样的布局，可以实现机构运动平台2个转动运动的解耦，且(U+UPS)P支链的闭环部分移动副与主干部分移动副的运动亦解耦，使整个机构的运动实现弱耦合。

2 机械手的机构学建模

2.1 坐标系定义及姿态描述

由图1可以看出，A1是(U+UPS)P支链的主干部分UP链的万向副回转中心点，A2是(U+UPS)P支链的闭环部分UPS链的万向副回转中心点，A3是独立UPS支链的万向副回转中心点。B1是运动平台与UP链的轴线交点，B0是中间连接杆轴线与UP链的轴线交点，B2是(U+UPS)P支链的闭环部分UPS链与中间连接杆连接球面副的回转中心点。用参数表示机构的主要结构尺寸为：A1A2=A1A3=a，B0B2=b，B1B3=c，A1B0=e，每个支链的长度AiBi=li(i=1,2,3)。以A1为原点建立机构固定参考坐标系A1xyz,其中，x轴与点A1、A3的连线共线；z轴与点A1、A2、A3所张成的平面垂直，方向如图1所示；y轴方向满足右手定则。以B1为原点建立机构运动坐标系B1upw，其中，w轴与UP链的轴线重合，方向如图1所示；u轴与运动平台上的点B1、B3的连线共线；p轴方向满足右手定则。另外，建立UP链的本地坐标系A1u1p1w1，其中，w1轴与点A1B1的连线共线，方向如图1所示；p1轴与点A1处的万向副远离固定平台的回转轴线重合；u1轴方向满足右手定则。定义运动平台的初始位姿为：运动平台与固定平台平行，且二者之间距离位于总变化范围的中间值h。因为运动平台与UP链末端固接在一起，所以选择点B1为运动平台参考点。

通过前文对机构坐标系的定义可知，坐标系B1upw相对于固定参考坐标系A1xyz的姿态可以通过2次旋转变换实现：先绕x轴旋转角度α，再绕p1轴旋转角度β，运动平台的旋转矩阵R可以描述为

(1)

式中，u、p、w分别为坐标轴u、p、w在固定坐标系A1xyz中的单位矢量；rot表示旋度。

2.2 位置反解

机械手的位置反解是通过其运动平台参考点B1在固定坐标系A1xyz中的位置矢量l1=(x,y,z)T，求出各支链总长度li(i=1,2,3)和运动平台姿态角α、β。在固定坐标系A1xyz中，建立矢量链闭环方程

l1=l1w1

(2)

ew1=a2+l2w2-b

(3)

l1=a3+l3w3-c

(4)

式中，wi(i=1,2,3)为支链i的单位矢量;e为A1B0的长度；a2为矢量A1A2；a3为矢量A1A3；b为矢量B0B2；c为矢量B1B3。

对式(2)～式(4)两端同时取范数可得

(5)

l2=‖ew1+b-a2‖

(6)

l3=‖l1+c-a3‖

(7)

根据矢量运算关系，可知w=w1=l1/l1=(wx,wy,wz)T

另外，根据式(1)可以计算出坐标系B1upw相对于固定坐标系A1xyz的姿态角为

(8)

将式(8)代入式(5)～式(7)即可求解出各支链的总长度值。

2.3 速度映射模型

建立运动平台的速度矢量与各支链驱动速度之间的传递模型，对式(2)～式(4)两端关于时间t求导数可得

(9)

(10)

(11)

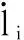
对式(9)～式(11)两端分别点乘wi(i=1,2,3)得

(12)

(13)

(14)

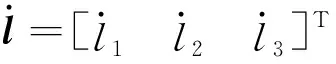
简写为

(15)

式中，J为机构的驱动雅可比矩阵,J∈R3×6。

将式(9)两端同时叉乘w1可得

因UP链无法绕其自身轴线旋转，故

ω=(w1×v)/l1

(16)

将式(16)代入式(13)、式(14)可得

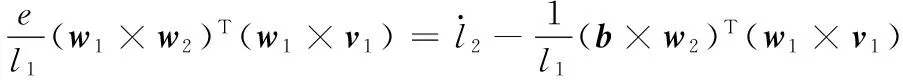
(17)

(18)

因为bTw1=0、cTw1=0，故式(17)、式(18)变为

(19)

(20)

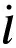
简写为

(21)

式中，Jv为机构的驱动线速度雅可比矩阵，Jv∈R3×6。

约束映射传递关系是建立机构的自身结构约束力/力矩与其输入之间的传递模型，根据少自由度机构的运动平台运动旋量分析方法，可知机械手的运动平台旋量系与UP链的运动旋量系一致，所以运动平台的瞬时旋量系在运动坐标系B1upw中的描述为

(22)

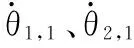
根据旋量系的对偶关系，可以得到机械手的运动平台约束旋量系为

(23)

对式(22)、式(23)计算互易积：

(24)

将式(24)写成矩阵形式可得

Jr∘$p=0

(25)

式中，Jr为机构的约束雅可比矩阵，Jr∈R3×6。

将式(25)中Jr单独描述可得

Jr的每个行向量代表运动平台的一个约束旋量。

2.4 静力学模型

定义运动平台输出驱动广义力为Fq=[FTMT]T，机械手的驱动输入广义力为τq=[τq1τq2τq3]T，根据虚功原理可得

(26)

将式(15)代入式(26)就可以推导出机械手的驱动静力学方程

Fq=Gqτq

(27)

式中，Gq为机械手的驱动力雅可比矩阵，且Gq∈R6×3。

定义运动平台的约束广义力为Fr=[fTmT]T，机械手的约束输入广义力为τr=[τr1τr2τr3]T，根据虚功原理可得

Fr=Grτr

式中，Gr为机械手的约束力雅可比矩阵，且Gr∈R6×3。

3 机械手的机构学性能分析

为了便于机构学分析，这里首先根据经验初选一组结构参数：a=230 mm，b=100 mm，c=60 mm，e=480 mm，h=800 mm，li∈(600,1 000)mm(i=1,3)，l2∈(300,600)mm。

3.1 工作空间分析

在进行工作空间分析之前，需要首先定义机构的约束条件，主要包括各支链长度、支链截面积半径、各运动副的工作范围等。

各支链长度变化范围为

limin≤li≤limaxi=1,2,3

(28)

式中，limin为各支链最小长度；limax为各支链最大长度。

各万向副2个回转轴线的转角ψi和θi的变化范围为

(29)

式中，ψmax、θmax为万向副的极限转角值。

各球面副3个回转轴线的转角ηi的变化范围为

0≤ηi≤ηimaxi=1,2,3

(30)

ηi=arccos(qili)

式中，qi为球面副的球窝座与运动平台固接点的单位法向矢量。

各支链移动伸缩套筒的实际直径d限定了各支链间的接近程度，则任意2个支链间的最短距离dij的变化范围为

dij≥di≠j且i，j=1,2,3

(31)

基于上述结构参数，根据式(2)～式(8)和式(28)～式(31)进行结构约束分析，采用渐变步长的搜索法在笛卡儿坐标空间内进行逐点计算并绘制出机械手的工作空间分布图，如图2所示。

图2 机械手工作空间3D分布图Fig.2 Workspace of manipulator

由图2可以看出，机械手的工作空间是近似的轴对称分布，主体由3个球冠交集构成，且各向分布均匀，说明该机构具有很好的各向同性；在垂直方向变化的同时水平截面先平稳增大后离散减小，可见其工作空间中垂直方向中、下部分布较好，可以作为结构设计的优选区域。

3.2 运动灵活性分析

首先，将雅可比矩阵的条件数k定义为运动学灵活性的一个评价指标[3]：

k=σmax/σmin

式中，σmax、σmin为雅可比矩阵的最大、最小奇异值。

基于初选结构参数，将机构工作空间坐标系进行网格分区，采用MATLAB计算评价指标k在机构工作空间内的分布，如图3所示。

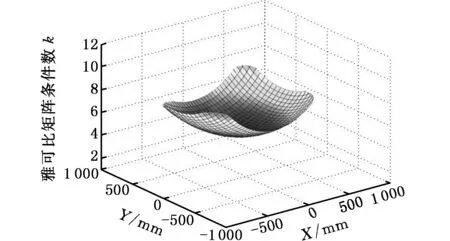
图3 雅可比矩阵条件数k在工作空间分布图Fig.3 Distribution map of conditional number k of Jacobi matrix in workspace

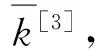
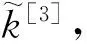
式中，V为工作空间函数。

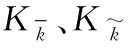
3.3 静力承载性能分析

(32)

(a)a与的关系

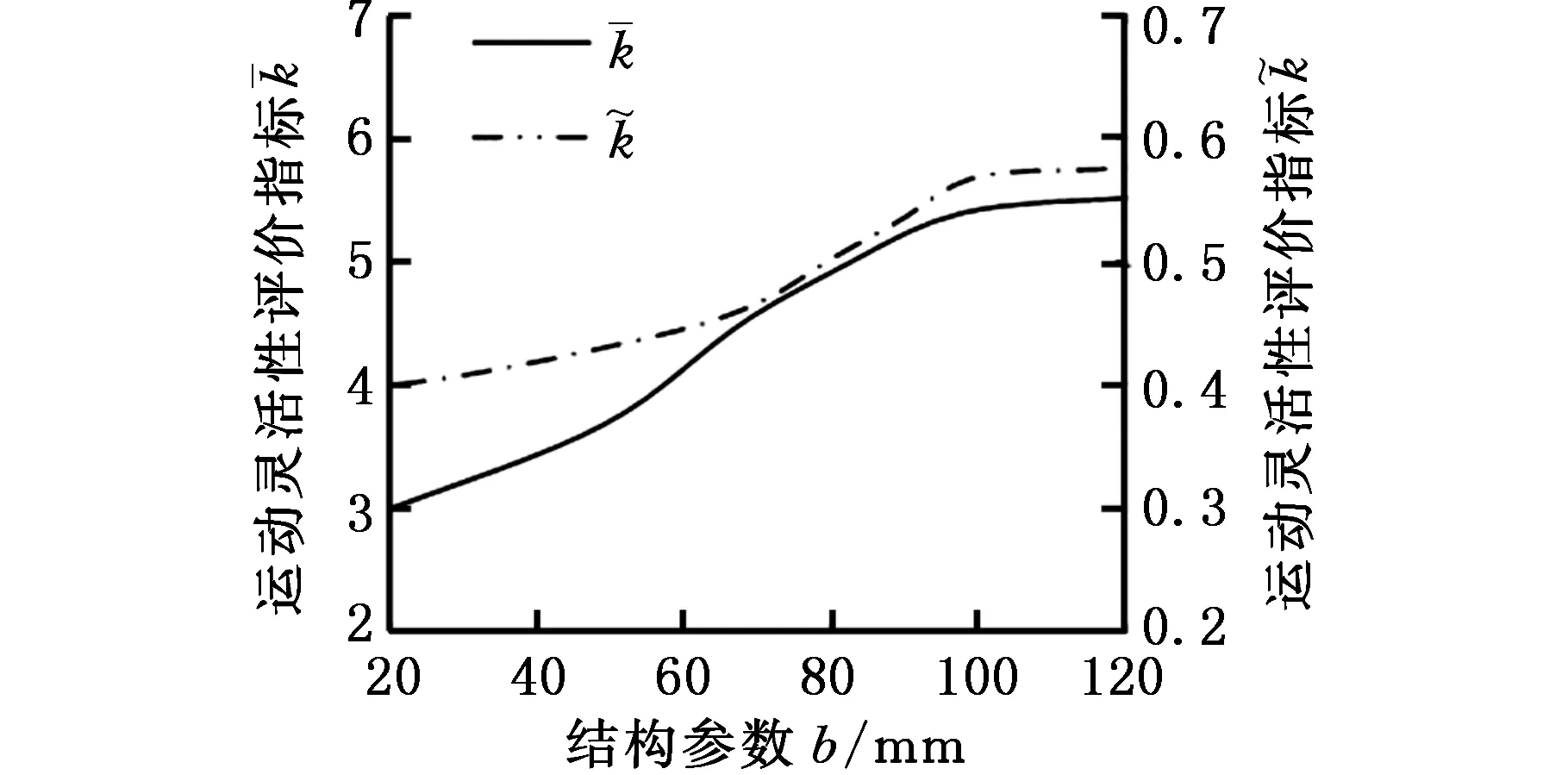
(b)b与的关系

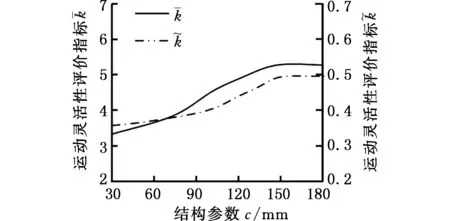
(c)c与的关系

(d)e与的关系图4 结构参数与机构运动灵活性评价指标关系图Fig.4 Relationship between structural parameters and moving flexibility capacity evaluation indexes

式中，GqF、GqM分别为机构的驱动力、力矩雅可比矩阵，GqF∈R3×3，GqM∈R3×3。

对式(32)取范数为

如果输入力为单位量，那么

引入拉格朗日算子如下：

(33)

式中，λF、λM为拉格朗日乘子。

通过式(33)可以计算出输出力、力矩的极值条件：

(34)

通过式(34)可以计算出输出力、力矩的极值为

(35)

式中，λFmax、λFmin、λMmax、λMmin分别为GqF、GqM的最大、最小奇异值。

定义机械手的一个驱动静力承载性能指标为

ηF=‖F‖max

定义机械手的另一个驱动静力承载性能指标为

式中，ηFR为力的最大值和最小值之差的比例关系。

把a、b、c、e选取为关键结构参数，绘制出结构参数与驱动静力承载性能评价指标关系变化曲线，如图5所示。

由图5可以看出，ηF、ηFR值随a值增大而波动增大，说明a值变化对ηF、ηFR的影响较大；ηF、ηFR值随b值的增大而波动减小；ηF、ηFR值随c值增大而减小，且减小到一定数值后，受其他约束影响变化趋缓；ηF、ηFR值随e值增大而缓慢增大。

4 机械手的设计及加载实验

4.1 机械手的实验样机本体设计

机械手的结构参数选取属于多性能指标、多结构参数的复杂系统，对于此类系统文献[18]提出一种基于性能评价指标的蒙特卡罗法对各结构参数进行抽样，然后以各性能评价指标为目标函数，通过数学工具计算和分析抽样结构参数值的分布规律，评估各性能指标的概率模型数值，然后根据概率值选取能够使各评价指标取值均较好的结构参数值。

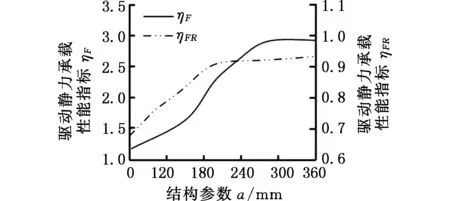
(a)a与ηF、ηFR的关系

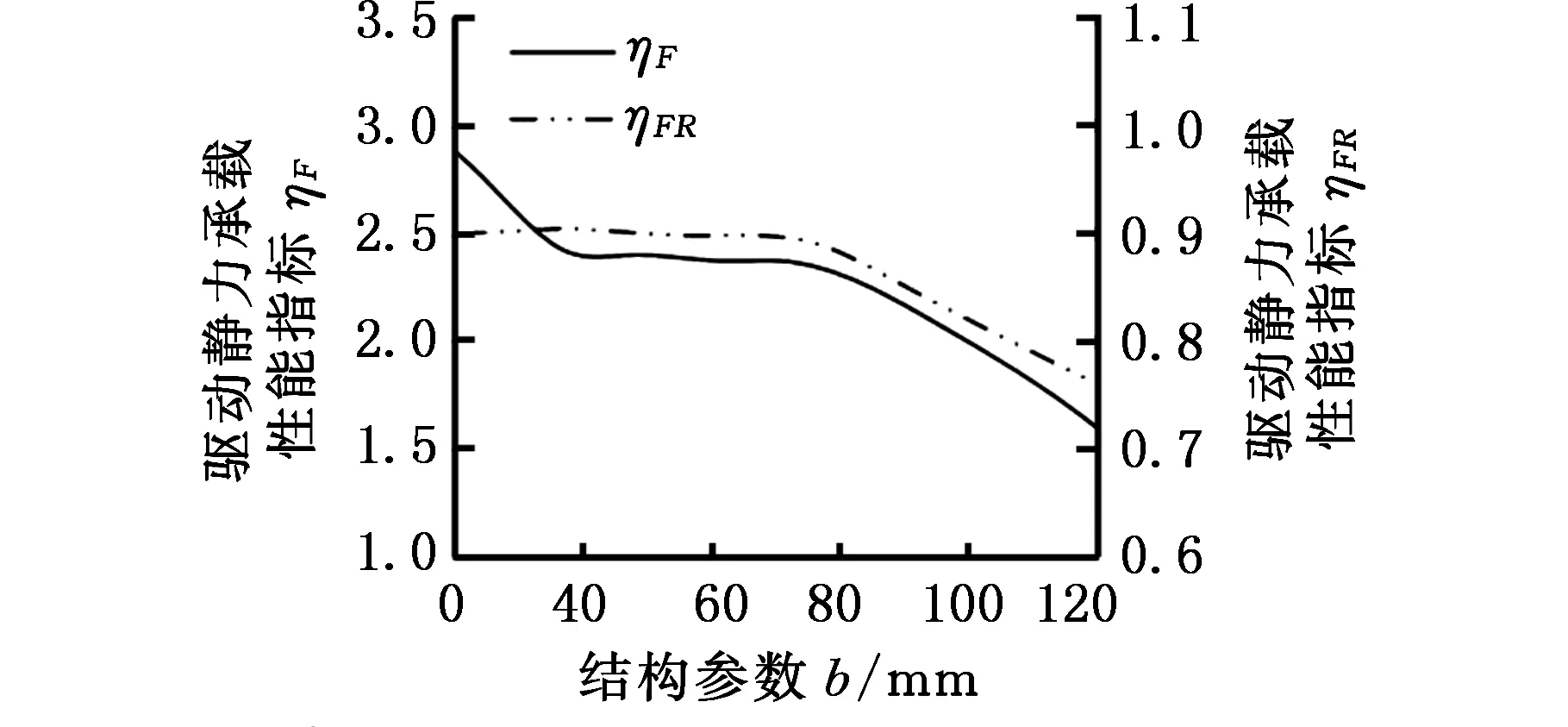
(b)b与ηF、ηFR的关系

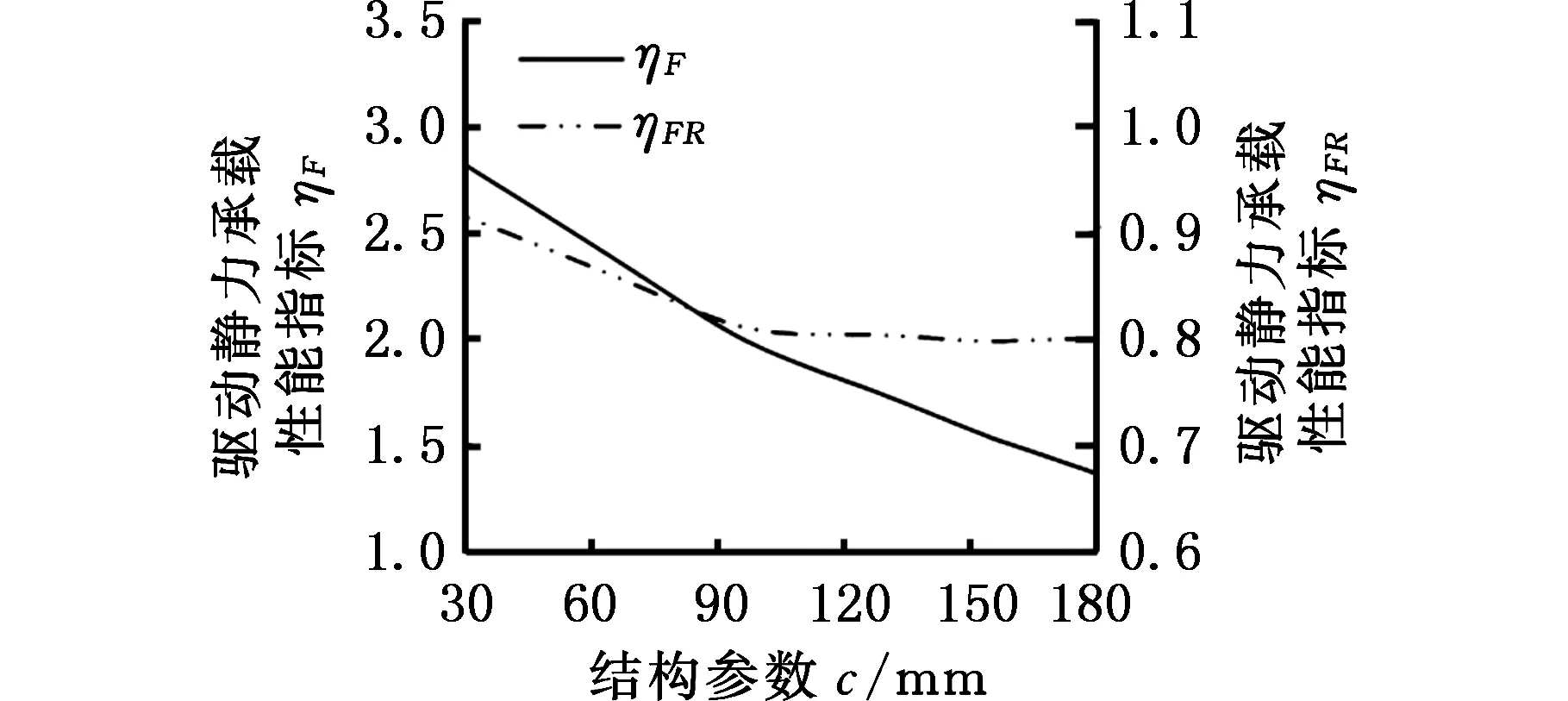
(c)c与ηF、ηFR的关系

(d)e与ηF、ηFR的关系图5 结构参数与静力承载性能评价指标关系图Fig.5 Relationship between structural parameters and static bearing capacity evaluation indexes

(a)a概率图 (b)b概率图

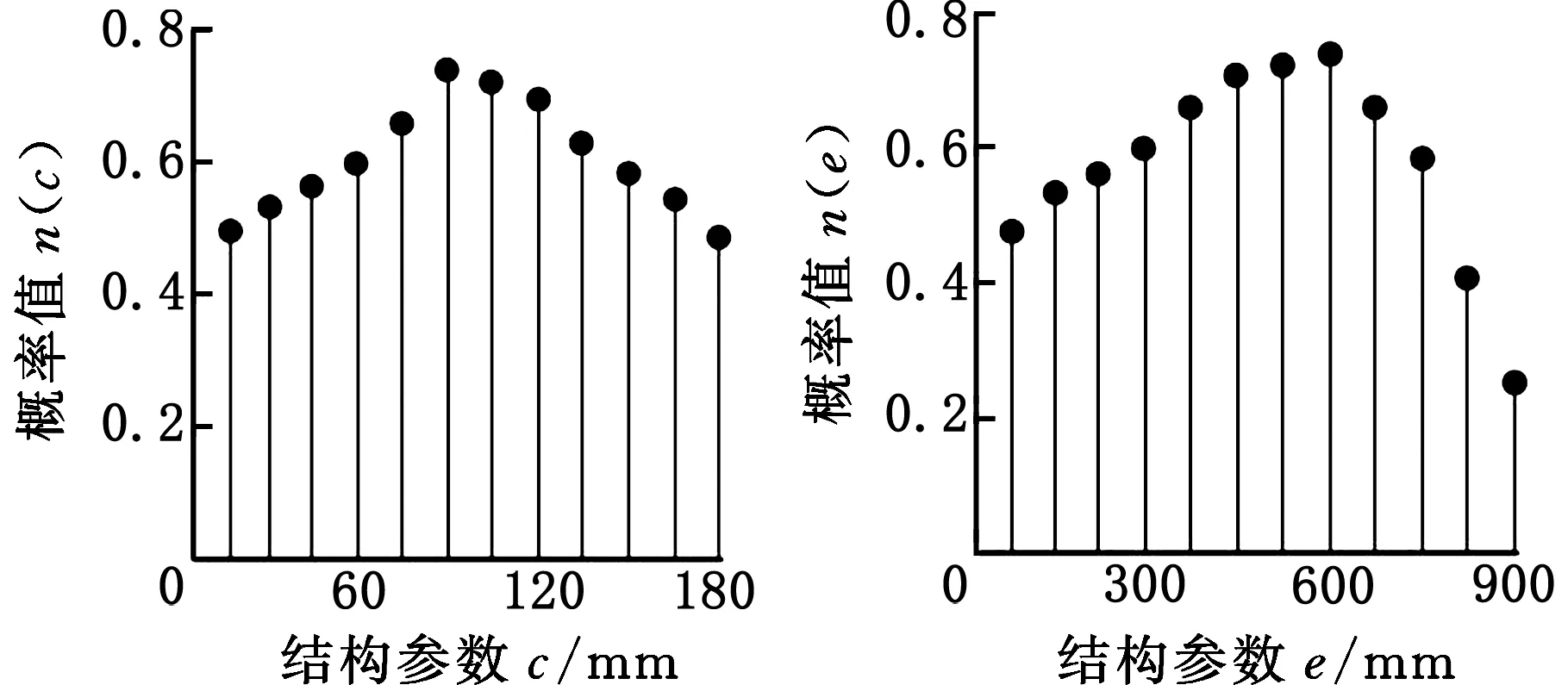
(c)c概率图 (d)e概率图图6 结构参数概率分布图Fig.6 Probability distribution diagram of structural parameters

分析图6可以获得各结构参数的优选值区间，通过权衡各评价指标与各结构参数优选值区间的重叠区域，从而确定一组兼顾各方面性能的结构参数值，如表1所示。

采用表1结构参数值，结合制造工艺因素，设计出3-DOF机械手方案，如图7所示。

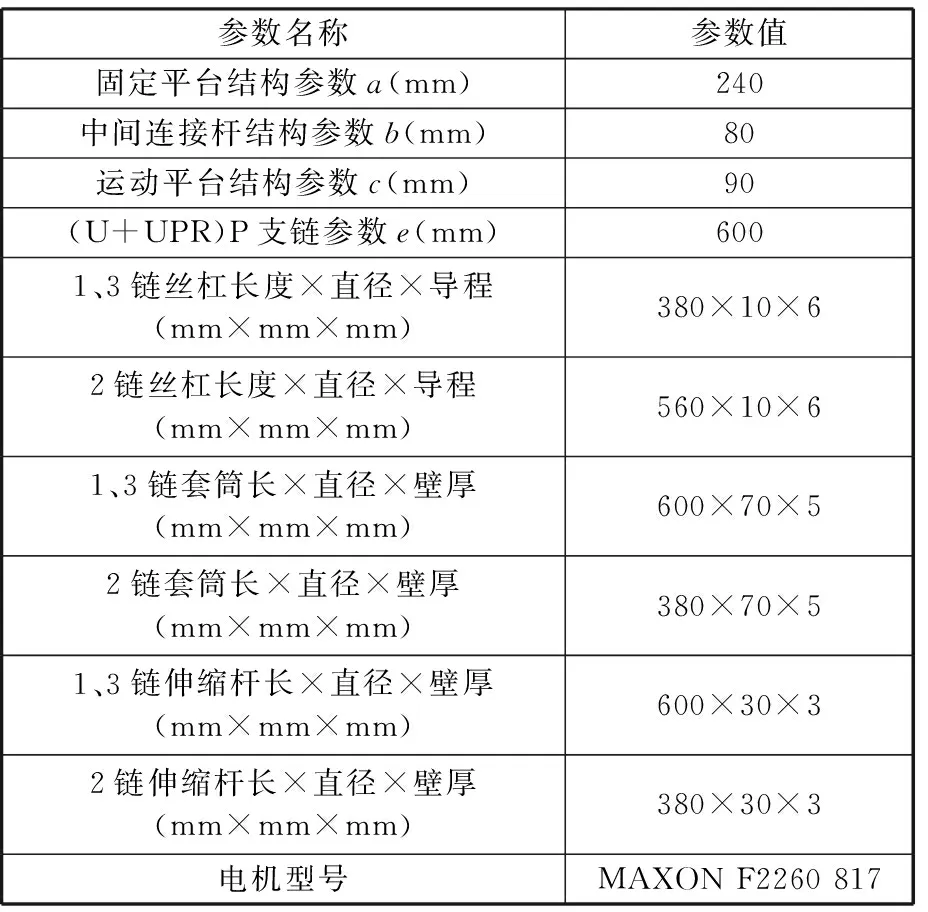
表1 机械手样机结构参数Tab.1 Structure parameters of manipulator prototype

1.基座 2.固定平台 3.万向副 4.丝杠电机 5.丝杠 6.丝杠螺母 7.套筒 8.伸缩杆 9.球面副 10.运动平台 11.电主轴 12.打磨叶轮 13.轮毂 14.夹具 15.中间连接杆图7 机械手设计方案图Fig.7 Design scheme of manipulator

基于图7的设计方案，研制出3-DOF机械手的实验样机，如图8所示。

1.固定平台 2.万向副 3.电机架 4.丝杠 5.丝杠螺母 6.套筒 7.伸缩杆 8.球面副 9.手腕 10.运动平台 11.中间连接杆 12.球面副图8 机械手实验样机图Fig.8 Experimental prototype of manipulator

4.2 实验样机本体的力学加载实验

为了验证本文研制的机械手在打磨载荷作用下的承载能力和结构变形情况，采用FANUC-R0iB机器人及配套的六维力/力矩传感器作为力学加载实验测量标定工具。基于FANUC-R0iB机器人的机械手力学标定系统(图9)，该机器人从重复定位精度为0.001 mm、姿态误差为0.01°，基于这样的精度级别，可完成对机械手的位置和姿态力学加载实验。标定系统主要由工业机器人R0iB、机器人手腕的力学标定传感器、机械手实验样机和标定系统基座组成。

在测量标定时，将机器人手腕安装的力学标定传感器与机械手的手腕平台固接，使机器人工作于软伺服模式。首先，通过机器人测量出机械手腕在其工作空间内采样点不受外力时的位姿精确坐标值。然后，通过机器人手腕的六维力/力矩传感器施加给定的模拟打磨外载荷τ=[FTMT](外力/力矩值)，并在此外力/力矩状态测量机械手腕位姿的变形量，从而整理出机械手在其工作空间内各采样点在给定外力/力矩时的变形量数据。为了保证力学标定精度，将R0iB机器人与机械手的固定平台放置在同一个大基座板上，从而使二者间没有相对位姿变化发生。

将实测的各采样点在模拟打磨外部载荷作用下变形量进行统计，如表2所示。

由表2可以看出，对于位置变形，各采样点的实测值变形量均小于0.015 mm，而且各采样点之间的实测变形值波动较小，说明该机械手的在外部载荷作用下的位置力学性能基本达到了设计要求。对于姿态变形，各采样点的实测值变形量均小于0.15°，而且各采样点之间的实测变形值波动较小，说明该机械手的在外部载荷作用下的姿态力学性能基本达到了设计要求。通过表2中对机械手在模拟打磨外载荷作用下的实测变形量可知，机械手本体实验样机的力学性能基本达到了设计要求。

(a)采样点1 (b)采样点2

(c)采样点3 (d)采样点4图9 机械手力学加载标定系统Fig.9 Mechanical loading calibration system of manipulator

采样点位置变形(Δx、Δy、Δz)(mm)姿态变形(Δα、Δβ、Δγ)(°)1(0.013 0.012 0.013)(0.11 0.12 0.11)2(0.013 0.012 0.011)(0.10 0.12 0.13)3(0.013 0.015 0.012)(0.12 0.10 0.11)4(0.011 0.013 0.013)(0.09 0.11 0.08)5(0.013 0.012 0.013)(0.10 0.12 0.08)6(0.011 0.013 0.013)(0.12 0.11 0.11)7(0.013 0.015 0.013)(0.12 0.09 0.08)8(0.012 0.013 0.011)(0.11 0.09 0.12)9(0.013 0.013 0.012)(0.10 0.12 0.11)10(0.013 0.013 0.012)(0.11 0.08 0.11)

5 结论

(1)提出了一种用于轮毂打磨的3-DOF并联机械手，对机械手的机构进行了运动学和静力学建模，通过矢量闭环方程获得了机构的速度雅可比矩阵，并基于此推导出机构的驱动、约束力雅可比矩阵。

(2)分析了机械手的工作空间，在定义运动灵活性评价指标的基础上对机构进行了运动灵活性分析，并计算出机构的各结构参数与其运动灵活性评价指标之间的关系；通过定义静力承载性能指标对机构的静力学性能进行了分析，并计算出机构的各结构参数与其静力承载能力之间的关系；揭示了结构参数对机构的运动灵活性和静力承载能力的影响规律。

(3)综合考虑机构的各种性能评价指标，采用蒙特卡罗法建立出各结构参数的概率模型空间，选取一组综合性能较好的结构参数：a=240 mm，b=80 mm，c=90 mm，e=600 mm，1、3链套筒和伸缩杆长度均为600 mm，2链套筒和伸缩杆长度均为380 mm。基于这组结构参数，设计了3-DOF并联机械手，并研制出机械手的实验样机。

(4)采用一套高精度机器人力学标定系统对机械手实验样机进行了力学标定实验，表明位置变形均小于0.015 mm，姿态变形均小于0.15°，通过实验，验证了本文提出的机械手的结构正确性。

[1] 熊有伦. 智能制造[J]. 科技导报,2013,31(10):3. XIONG Youlun. Intelligent Manufacturing [J]. Science and Technology Review,2013,31(10):3.

[2] 蔡鹤皋. 对我国机器人产业发展的思考[J]. 集成技术,2015,4(5):1-4. CAI Hegao. Thinking on the Development of Robot Industry in China [J]. Integration Technology,2015,4(5):1-4.

[3] 孙一兰, 柳洪义, 王品. 导弹弹体内壁打磨机器人及其运动轨迹规划[J]. 中国机械工程,2009,20(7):838-843. SUN Yilan, LIU Hongyi, WANG Pin. Design of Missile Inner-wall Grinding Robot and Its Trajectory Planning[J]. China Mechanical Engineering,2009,20(7):838-843.

[4] 王平, 杨沿平, 邓晓. 基于模具表面抛光机器人系统的运动控制研究[J]. 中国机械工程, 2007,18(20):2422-2425. WANG Pin, YANG Yanping, DENG Xiao. Research on Calculation Method of the Static and Dynamic Characteristics of Magnetic Bearing Based on the Basic Solutions[J]. China Mechanical Engineering,2007,18(20):2422-2425.

[5] 刘建春, 陈雄风, 廖妮兰. 小型异构件抛光机运动系统分析[J]. 中国机械工程,2016,27(16):1039-1052. LIU Jianchun, CHEN Xiongfeng, LIAO Nilan. Motion System Analysis of Small Heterogeneous Parts Polishing Machine[J]. China Mechanical Engineering,2016,27(16):1039-1052.

[6] 刘少凤, 孙宗禹. 全球制造策略[J]. 中国机械工程,2001,12(1):114-119. LIU Shaofeng, SUN Zongyu. Global Manufacturing Strategy[J]. China Mechanical Engineering,2001,12(1):114-119.

[7] 尹咸. 整体螺旋桨机器人砂带磨削加工工艺技术及试验研究[D]. 重庆: 重庆大学,2015. YIN Xian. Research on Technology and Control Scheme of Robotic Abrasive Belt Polishing for Integrated Propeller[D]. Chongqing: Chongqing University,2015.

[8] 崔宝军. 新型上海大众轮毂制造工艺优化及实践[D]. 秦皇岛: 燕山大学,2015. CUI Baojun. New Manufacturing Process Optimization and Practice for Hub of Shanghai Volkswagen[D]. Qinhuangdao: Yanshan University,2015.

[9] 杨仲升, 黄云, 邹莱. 铝合金轮毂机器人光整加工控制技术研究[J]. 中国机械工程,2016,27(14):1857-1862. YANG Zhongsheng, HUANG Yun, ZOU Cai. Analysis of Gas Flow Mechanism and Pressure Characteristics between Plates in Micro Scale[J]. China Mechanical Engineering,2016,27(14):1857-1862.

[10] 赵菀. 汽车轮毂数控抛光机床的设计与研究[D]. 武汉: 华中科技大学,2014. ZHAO Yuan. Research and Design for NC Polishing Machine of Vehicle Wheels[D]. Wuhan: Huazhong University of Science and Technology,2014.

[11] 王旭. 五轴数控抛光机CAM技术研究[D]. 秦皇岛: 燕山大学,2011. WANG Xu. Researching of Five-axis NC Polishing Maching CAM[D]. Qinhuangdao: Yanshan University,2011.

[12] 陈义. 铝轮毂曲面成套机械抛光技术研究[D]. 武汉: 华中科技大学,2010. CHEN Yi. Research on Complete of Mechanical Polishing Technology for Aluminum Wheel Hub Surface[D]. Wuhan: Huazhong University of Science and Technology,2010.

[13] 李研彪, 金振林, 计时鸣. 一种新型3-DOF 串并混联拟人机械手的研制[J]. 中国科学,2009,39(12):1983-1991. LI Yanbiao, JIN Zhenlin, JI Shiming. Design of a novel 3-DOF hybrid mechanical arm[J]. Science China,2009,52(12):3592-3600.

[14] 李彬, 黄田, 刘海涛. Exechon混联机器人的三自由度并联机构模块位置分析[J]. 中国机械工程,2010,21(11):2785-2789. LI Bin, HUANG Tian, LIU Haitao. Position Analysis of a 3-DOF PKM Module for a 5-DOF Hybrid Robot Exechon[J]. China Mechanical Engineering,2010,21(11):2785-2789.

[15] 刘海涛. 少自由度机器人机构一体化建模理论、方法及工程应用[D]. 天津: 天津大学,2010. LIU Haitao. Unified Parameter Modeling of Lower Mobility Robotic Manupulators: Theory, Methodology and Application[D]. Tianjin: Tianjin University,2010.

[16] 李研彪. 新型6-DOF串并混联拟人机械手的性能分析与设计[D]. 秦皇岛: 燕山大学,2009. LI Yanbiao. Analysis and Design of a Novel 6-DOF Hybrid Mechanical Arm[D]. Qinhuangdao: Yanshan University,2009.

[17] 金振林, 曹舜, 高峰. 新型机器人肩关节及其运动学分析[J]. 中国机械工程,2009,20(14):1639-1642. JIN Zhenlin, CAO Shun, GAO Feng. Design and Kinematics Analysis of a Novel Robot Shoulder Joint [J]. China Mechanical Engineering,2009,20(14):1639-1642.

[18] 秦利. 考虑重力效应的空间机器人系统建模与控制研究[D]. 秦皇岛: 燕山大学,2014. QIN Li. Research on Modeling and Control for Space Robot System with Gravity Effect Consideration[D]. Qinhuangdao: Yanshan University,2014.

[19] HAO F, MERLET J P. Multi-criteria Optimal Design of Parallel Manipulators Based on Interval Analysis [J]. Mechanism and Machine Theory,2005,40(2):157-171.

[20] TSAI L W. Solving the Inverse Dynamics of a Stewart-gough Manipulator by the Principle of Virtual Work [J]. Journal of Mechanical Design,2000(122):3-9.

[21] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006:277-283. HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Advanced Spatial Mechanism [M]. Beijing: Higher Education Press,2006:277-283.

[22] 曾达幸, 黄真. 基于螺旋理论的转动解耦并联机构型综合[J].中国科学,2011,41(5):585-591. ZENG Daxing, HUANG Zhen. Type Synthesis of the Rotational Decoupled Parallel Mechanism Based on Screw Theory [J]. Science China,2011,41(5):585-591.