金属腐蚀的多尺度计算模拟研究进展
2018-03-02董超芳徐奥妮李晓刚
魏 薪,董超芳,徐奥妮,李 妮,肖 葵,李晓刚
(北京科技大学 腐蚀与防护中心 教育部腐蚀与防护重点实验室,北京 100083)
1 前 言
金属的腐蚀受到材料因素、环境因素和界面状态的影响,任何单一因素或耦合条件的改变都可能造成腐蚀规律的变化[1],影响因素的复杂程度造成了腐蚀行为的多样性,其机理研究的难度也正源于此。伴随着计算机的发展,“计算和模拟”已经成为了继实验、形式理论之后的第3条发现新概念和机理的途径[2, 3]。在通过实验建立的腐蚀模型基础上,可以实现对点蚀[4-6]、晶间腐蚀[7]、应力腐蚀[8]、冲蚀[9, 10]、扩散传质[11, 12]和电极过程动力学[13]等的理论研究。近年来,随着试验观测技术的提高,扫描电化学显微镜(SECM)[14]、原子力显微镜(AFM)[15]、扫描开尔文力显微镜(SKPFM)[16]等微观观测仪器已经应用到了腐蚀研究中。这些仪器的观测尺度一般在1 mm到1 μm的范围内,可以细致到观测单个蚀坑的形貌,研究单个蚀坑周围的电位,这对揭示腐蚀的深层机理有很大的促进。观测手段的发展,为介观尺度下的腐蚀过程的建模和仿真提供了试验数据基础。
另一方面,受反应时间和尺度限制,大多数腐蚀实验研究方法,并不能直接观察材料的腐蚀萌生行为。研究者只能通过实验获得的数据进行分析进而推断反应发生过程,这一方法容易发生错误致使人们不能正确获得真正的腐蚀机理,从而不能正确指导材料的设计与使用。原位测试技术的发展在某种程度上解决了部分问题,但由于其对试样和实验条件要求极高并不能广泛的应用。近年来,理论计算用软件得到了迅速发展,使得腐蚀机理的研究取得了突破性的进展,对材料的设计和使用具有积极的指导作用。目前,腐蚀领域中应用较广泛的计算方法包括基于密度泛函的第一性原理和分子动力学方法、基于牛顿力学的分子动力学计算、基于电化学的热力学和动力学计算以及基于断裂力学的有限元方法等。
计算方法的选择与所研究对象的尺度有关,已有从原子到宏观尺度的方法包括:第一性原理计算、Monte Carlo方法、分子动力学、元胞自动机、有限元、边界元等,其中第一性原理计算方法受到较大关注。Di Stefano等[17]利用基于密度泛函的第一性原理计算方法研究了∑3(111)[-110]晶界和∑5(210)[001]晶界与H的相互作用,结果表明:这两种晶界与H原子的相互作用行为截然不同。密排的∑3晶界既不能捕获H原子也不能促进其在晶界的扩散,在材料内部充当二维的扩散阻挡层;而∑5晶界能够提供大量的H溶解位,且相比于块体材料,H原子沿∑5晶界的扩散系数提高了两个数量级。Kulkoua等[18]利用第一性原理计算方法研究了H与B2结构TiFe合金的相互作用,通过计算H原子晶界和自由表面的吸附能和偏聚能表明,H有助于晶间开裂的发生。
本文将对不同尺度下金属腐蚀研究的计算方法进行总结,并以大气环境下铝合金的腐蚀与氢致开裂为计算对象,利用第一性原理和内聚有限元的跨尺度计算方法,研究了氢原子偏聚导致的晶间裂纹的萌生与扩展行为,将第一性原理计算获得的晶界结合能输入到内聚有限元计算中,实现了从原子尺度到宏观尺度的跨尺度计算。
2 计算方法在金属腐蚀研究中的应用
2.1 第一性原理计算方法及其在腐蚀研究中的应用
随着量子理论的建立和计算机技术的发展,人们希望能够借助计算机对微观体系的量子力学方程进行数值求解,然而量子力学的基本方程—薛定谔方程的求解是极其复杂的。然而,电子密度泛函理论(DFT)的确立[19, 20]克服了这种复杂性。电子密度泛函理论是20世纪60年代在Thomas-Fermi理论的基础上发展起来的量子理论的一种表述方。传统的量子理论将波函数作为体系的基本物理量,而密度泛函理论则通过粒子密度来描述体系基态的物理性质。密度泛函理论是一种完全基于量子力学的从头算理论,但是为了与其他的量子化学从头算方法区分,人们通常把基于密度泛函理论的计算叫做第一性原理。
在密度泛函理论中,所有的近似都被集中到称为交换相关能的一项上,所以密度泛函理论的精度直接由交换相关能量泛函的近似形式决定。寻找更好的交换相关近似就成为密度泛函理论体系发展的一条主线。交换相关能量泛函的一个最初的简单近似方法是局域密度近似(LDA),即用具有相同密度的均匀电子气的交换相关泛函作为对应的非均匀系统的近似值,这样一个简单近似往往能给出很好的结果。如果进一步分别考虑不同自旋分量的电子密度,可得到自旋极化的局域密度近似L(S)DA。尽管L(S)DA获得了巨大的成功,但是也有许多不足之处,比如系统地高估结合能。在L(S)DA基础上的改进有广义梯度近似(GGA)。在GGA近似下,交换相关能是电子密度及其梯度的泛函。构造GGA交换相关泛函的方法分为两个流派。一个是以Becke 为首的一派,认为“一切都是合法的”,人们可以任何理由选择任何可能的泛函形式,而这种形式的好坏由实际计算来决定。通常,这类泛函的参数由拟合大量的计算数据得到。另外一个流派以Perdew 为首,他们认为发展交换相关泛函必须以一定的物理规律为基础,这些规律包括标度关系、渐进行为等。基于这种理念构造的一个著名的GGA泛函是PBE泛函[21],也是现在用得最广泛的GGA泛函之一。电荷密度泛函理论在局域电荷密度近似或是梯度修正的版本,这是由Perdew和Wang所发展的GGA。DFT所描述的电子气体交互作用被认为是对大部分的状况都是精确的,并且他是唯一能实际有效分析周期性系统的理论方法。梯度修正的方法在研究表面的过程,小分子的性质,氢键晶体以及内部空间的晶体是比较准确的。众所皆知,LDA会低估分子的键长或者键能,以及晶体的晶格参数,而GGA会补救这些缺点。而GGA在里斯晶体会过度修正LDA结果。当LDA与实验符合非常好的时候,GGA会高估晶格长度。
利用第一性原理计算方法研究金属材料在原子尺度的腐蚀行为对探究腐蚀机理有着十分重要的意义。基于密度泛函的计算方法可从原子之间相互作用的角度计算金属材料的固有性质,或描述金属基体或钝化膜表面与环境中分子或离子等之间的化学反应。
2.1.1 表面吸附导致钝化膜的形成与破坏
金属暴露于各类环境下,与气体或溶液中的气体和离子发生相互作用,具体宏观表现为金属氧化膜的形成与破坏以及金属表面与腐蚀性气体和离子的相互作用。由此可见,吸附对腐蚀行为影响显著,金属表面对气体或离子的吸附分为物理吸附和化学吸附。判断被吸附物与表面是否发生化学反应需要计算体系的电子性质,如态密度、电荷密度、电子局域函数、布局分析、Bader电荷分析等。
本课题组[22]利用密度泛函方法计算了H2O和SO2在面心立方金属Cu(111) 表面的单吸附和共吸附行为。通过对几何构型,能量,电荷转移及态密度的分析可得到以下结论。单分子H2O和SO2均不能与化学键的形式吸附在表面。对于共吸附构型,当覆盖度为0.25 ML时,H2O和SO2分子分别吸附在Cu(111)表面;当覆盖度增大到0.5 ML时,H2O分子解离为OH和H,其中OH吸附在表面,而H与SO2键合远离表面。
Guo等[23]利用第一性原理计算表明,H2O分子在Al(111)纯表面的解离能为248.32 kJ/mol,然而当存在预吸附O时,解离能降低到128.53 kJ/mol,说明O原子的存在大大降低了H2O在铝表面的解离能。基于密度泛函的计算能够有效的研究H2O与金属的相互作用,但是在计算中却存在一个严重的问题,那就是标准的密度泛函方法无法描述H2O分子与金属表面的弱相互作用[24]。目前,已有大量研究[25,26]证明在考虑H2O分子与金属表面相互作用时应考虑范德华色散力的作用。本课题组[27,28]采用范德华密度泛函计算方法研究了O2和H2O分子在Al(111)表面的单吸附和共吸附行为。结果表明,O2分子可自发解离,以O原子的形式吸附在表面,伴随着较大的吸附能;而H2O分子只能以分子的形式弱吸附在表面。同样地,预吸附的O原子仅能促进H2O分子的变形,大大降低其解离能垒,不能使其解离吸附。当O2分子存在时,且两个O原子同时与H2O分子中的H原子产生相互作用时,H2O分子解离为OH和H,吸附在金属Al(111)表面。通过对O2和H2O分子的共吸附行为的研究可知,Al表面钝化膜的形成机理为H2O分子的存在促进了吸附的原子O由表面向内部的渗透而增厚,而不是金属原子向外部的迁移。
Digne等[29]利用第一性原理计算的方法建立了γ-Al2O3表面模型。利用密度泛函方法,作者详细研究了γ-Al2O3三种表面(100)、(110)和(111)的酸基性质,并考虑了与温度相关的羟基化表面的覆盖度。模拟与大量实验结合解决了在红外光谱中出现的OH-伸缩频率的问题。研究还确定了酸化表面位的精确本性。酸化的强度可以通过模拟目标分子,如CO,和计算表面电子性质来量化。这些结果严重挑战了以前的无缺陷尖晶石γ-Al2O3的表面模型并建立了γ-Al2O3酸化性质更为严格的描述。本课题组的研究成果[30]利用考虑强关联效应的密度泛函方法研究了SO2分子在金属镍表面钝化膜NiO(111)表面的吸附行为,结果表明,表面O空位的存在大大加强了表面对SO2分子的吸附,进一步说明表面钝化膜的完整性对于材料耐蚀性的关键作用。这一系列的研究充分说明第一性原理可用于铝合金与大气环境中气体相互作用的计算。
2.1.2 氢原子在界面处的偏聚
材料内部存在大量的晶界以及第二相与基体的界面,这些界面属于高能区。在腐蚀环境下,腐蚀优先发生在界面处,且氢原子在界面的聚集导致氢脆的发生。因此,计算界面的结合能以及氢原子聚集对界面结合能的影响对研究应力腐蚀、氢致开裂等局部腐蚀机理具有重要的意义。Fernandea等[31]利用密度泛函与基于过渡态理论和热力学的静态模型相结合的方法研究了氢原子与金属钨的相互作用。该模型得到的与温度相关的数据有助于理解宏观实验获得的结果。研究结果有效的解释了实验测得的H扩散系数与密度泛函计算获得的结果存在偏差是由于空位浓度与温度的差异。Kristinsdóttir等[32]利用密度泛函方法研究了氢原子在23种过渡态金属密排表面的扩散行为。作者选择了第4、5和6周期,从Sc到Au,除了Mn、Tc和Hf的d-金属。氢原子在这些金属表面的势能面被建立,且从一个极小值到另一个极小值的能垒与微动弹性带计算相比较。结果表明,所有的扩散激活能相对低或从Pt/0.04 eV到Y和Zr/0.28 eV。作者还估计了隧道效应开始发生的温度。Ferrina等[33]利用周期自洽DFT-GGA(PW91)方法研究氢原子与17个过渡族金属表面,即面心立方金属的(100)和(111)面,密排六方金属的(0001)和体心立方金属的(100)和(110)的相互作用。计算得到与实验结果一致的几何结构和结合能。对于同一金属的密排面和较开放的表面,计算得到的结合能有很大的不同。同一金属不同亚表面的氢原子几何结构基本一样,但是结合能有很大不同。除了Ag和Au表面H的吸附相对于H2时放热的。对于所有研究的金属,H在亚表面层的优先吸附位没有在表面的优先吸附位稳定。H从表面到第一层亚表面的扩散激活能由两个表面热力学稳定性的差异控制。扩散从第一亚表面扩散进入下一层通常没有很大的热力学能垒,但有适当的动力学能垒。对于同一种金属,H在不同表面向内扩散的激活能垒也有很大的不同。Mao等[34]利用第一性原理和分子动力学方法研究了间隙原子H在Er2O3内的扩散,计算了H在块体材料,(001)表面和 Σ13 (4-3-1)/[111] 扭转晶界的扩散率和扩散能垒。结果表明,H在(001)表面的扩散比在块体材料和晶界处快。由DFT和MD方法估计的H扩散能垒高于由实验得到的沿晶界的能垒。这表明H在Er2O3内的扩散由晶界控制。
2.2 有限元方法及其在腐蚀研究中的应用
有限单元法是随着电子计算机的发展而迅速发展起来的一种现代计算方法。它是50年代首先在连续体力学领域-飞机结构静、动态特性分析中应用的一种有效的数值分析方法,随后很快广泛的应用于求解热传导、电磁场、流体力学等连续性问题。有限元法是一种为求得偏微分方程边值问题近似解的数值技术。它通过变分方法,使得误差函数达到最小值并产生稳定解。
ABAQUS是学术研究中使用最为广泛的有限元分析软件之一。ABAQUS基于其丰富的单元库,可用于模拟各种复杂的几何形状,并且拥有丰富的材料模型库,可用于模拟绝大多数常见的工程材料,如金属、聚合物、复合材料、橡胶、可压缩的弹性泡沫、钢筋混凝土以及各种地质材料。随着实验室实验方法得到很大发展的同时,有限元模拟方法也取得了很大的进展,除一般的线性和非线性有限元模拟,还出现一些新的有限元模拟技术。本文主要介绍内聚力单元(Cohesive elements)的有限元模拟方法。
ABAQUS提供一种内聚力单元,用以模拟两个部分之间的粘性连接,一般来说,它要求粘结材料尺寸和强度都小于粘结部分(比如多层复合材料的胶粘层),进而可以利用内聚力单元模拟材料的断裂。
这个单元似乎与C3D8实体单元的结构一致,但最大的区别在于横纵向尺寸的比例,C3D8单元在模拟这种大横纵比结构的时候,已经无法给出精确的解答了。这就是内聚力单元存在的意义,此外,从内聚力单元的变形机理来看,中面虽然能够承受拉伸和剪切应变,但并不能产生任何应力。因此,内聚力单元只能支持垂直于上下表面的牵引-分离破坏准则。当需要模拟诸如扁平结构破坏或者某结构沿一个平面撕裂这种工况的时候,内聚力单元提供了一种无需细化网格的解决方案,可以有效的降低网格数量,提高运算效率。
基于力学的有限元模拟在腐蚀中应用的研究并不是很多,大多数研究集中在材料表面和内部裂纹萌生和扩展问题,尤其是氢敏感体系。Simonovski等[35]提出了利用内聚单元法在晶粒尺度模拟晶间开裂行为的方法。该方法将0厚度的内聚力单元嵌入晶粒之中代表晶界。利用traction-seperation法则进行应力和晶界损伤的计算,结果表明,该方法能够有效的评价多晶体的晶间损伤和开裂行为。Scheider等[36]用内聚力有限元模型研究了氢扩散对裂纹扩展的影响。Pouillier等[37]利用内聚力模型模拟铝合金的氢致晶间开裂行为,所得结果与电子背散射技术测得的结果一致。
综上所述,计算模拟方法在腐蚀领域得到了广泛的应用,并取得了突破性的进展。计算模拟可为实验结果提供理论指导,也可为数据分析提供依据。因此,计算模拟方法是研究腐蚀行为与机理的有效手段。
2.3 跨尺度计算与模拟方法研究进展
金属结构材料在环境中腐蚀的过程从表面对腐蚀性离子的吸附、点蚀与微裂纹的萌生到点蚀坑与裂纹的形成,整个过程从肉眼难以察觉的原子尺度到可观察的宏观尺度。通常来讲,受到反应时间和尺度的限制,原子尺度的反应很难利用实验手段进行观测,这也导致原子尺度的计算与模拟结果很难得到验证。因此,建立原子尺度到宏观尺度的跨尺度的计算方法,将原子尺度的输出结果输入到宏观尺度的计算之中,这样既解决了小尺度实验难以实现的问题,又可对宏观尺度的结果进行实验验证进而间接验证原子尺度的计算结果。除此之外,腐蚀环境复杂多变,利用跨尺度的计算与模拟方法能够对单一因素的影响进行系统研究。
近年来,跨尺度计算已经出现在不同领域的研究之中。多尺度的计算方法一般可分为尺度分离和尺度间耦合两种,前者着眼于采用不同尺度来分析对象的不同部分,后者注重寻找尺度之间的关联[38]。通常来讲,尺度之间的划分为宏观(>10-4m)、介观(介于10-6m与10-4m之间)、微观(介于10-7m到10-6m)和纳观(<10-7m)[39]。对于腐蚀计算而言,既需要利用不同尺度的计算方法研究腐蚀发生的不同阶段,也需要探究不同尺度之间的耦合关系,通过选择合适的计算方法对腐蚀的行为与机理进行研究。目前,常见的跨尺度计算模型大多集中在对材料的塑性形变和断裂过程的研究,如本课题组[40]利用第一性原理与内聚有限元相结合的跨尺度计算方法研究了铝合金的晶间开裂行为。首先,利用第一性原理研究了H原子在Al内部和晶界处的吸附、溶解和扩散行为,结果表明H原子优先溶解在晶界间隙位且晶界为H原子的快速扩散通道;其次,将不同浓度的H原子引入到晶界间隙位并计算其晶界结合能,结果表明晶界结合能,即晶界强度随H原子浓度的增加而线性下降;最后,将第一性原理计算获得的晶界结合能作为断裂能输入到内聚有限元计算之中,模拟铝合金的晶间开裂行为。
3 铝合金腐蚀与氢致开裂的模拟计算
3.1 铝钝化膜点蚀萌生机理
铝表面覆盖的氧化物在溶液中或在潮湿空气中,会吸附环境中的H2O分子形成羟基化的水合表面。当溶液中存在Cl-时,它会与溶液中的OH-在钝化膜表面发生竞争吸附形成Me-Cl-或是MeO(H)-Cl-的产物,产物的生成导致钝化膜中的金属离子与表面的结合力降低从而易于离开表面溶于溶液之中。随着吸附反应的发生,更多的金属阳离子迁移到溶液中导致钝化膜快速减薄,降低其耐蚀性能。关于钝化膜的局部减薄造成点蚀的机理已被广泛讨论过,但尚未达成一致的说法,尤其是在原子尺度的机理研究还未见报道。本部分利用基于密度泛函的第一性原理计算研究Cl-在金属铝钝化膜表面的吸附和向亚表面渗透的过程。通过对取代和渗透反应的构型、能量和能带结构的分析来探究Cl-与钝化膜反应的本质及其导致钝化膜破裂的机理。
图1a为Cl-取代羟基化γ-Al2O3(010)表面OH-的构型图。随着数值OH-/Cl-的减小,表面发生不同程度的重构。对于OH∶Cl>8∶8,Cl-取代的OH-来自解离的H2O,对氧化膜本身的结构未产生明显的影响。对于OH∶Cl=2∶14,有14/16的表面OH-吸附位被取代,由构型图可知表面第一层Al原子均被拉出表面,发生明显的重构现象。对于OH∶Cl=0∶16来说,表面OH-均被Cl-取代,第一层表面原子与Cl-形成腐蚀产物。图1b为随表面Cl-浓度的增加Cl-取代OH-的能量变化,当表面Cl-浓度较低时(小于OH∶Cl=12∶4中所示浓度),随着表面Cl-浓度的增大取代能负移,说明Cl-浓度的增加促进其在表面的吸附;当表面Cl-浓度介于OH∶Cl=12∶4和OH∶Cl=8∶8之间时,随着Cl-浓度的增加取代能正移,说明当表面存在一定吸附Cl-时,后续的Cl-吸附反应难度增加;当表面Cl浓度大于OH∶Cl=8∶8所示,Cl开始取代表面OsH,取代的难度进一步加大。造成能量正移的原因为表面吸附Cl-之间的静电斥力。当表面全部被Cl-取代时,取代能略有降低,但仍明显高于低Cl-浓度时。这是因为全部取代使得表面处于对称结构,降低了静电斥力间的不均匀,使得吸附结构变得稳定。综上所述,吸附的Cl-和OH-对后续Cl-的取代反应均有阻碍作用,控制吸附反应发生的因素为表面吸附离子之间的静电斥力。
Cl-取代表面OH-的反应为放热反应,随着取代Cl-浓度的增加,取代能正移,反应驱动力减小。若Cl-取代羟基化γ-Al2O3(010)表面的吸附的来自H2O解离的OH-,则对钝化膜的结构无明显影响;若取代钝化膜本身与H+结合成的OH-时,则发生明显结构变化,随着取代Cl-浓度的增大,表面Al与Cl-结合生成无序氯化物层。
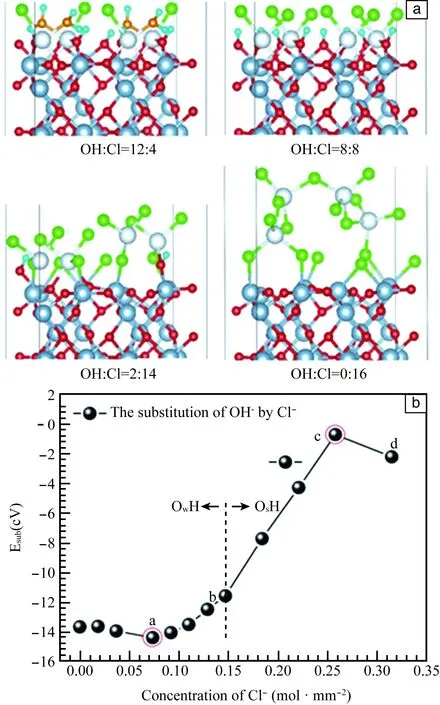
图1 Cl-在水合γ-Al2O3(010)表面发生取代反应:(a)原子构型图; (b)能量随表面Cl-浓度的变化Fig.1 Substitution reaction between chloride ions and hydrous γ-Al2O3(010) surface: (a)atomic configuration diagram; (b)variation of energy as chloride ions’ concentration
3.2 氢原子的吸附、溶解和扩散
H原子能够在铝表面吸附并进入材料内部,溶解在间隙位。Al (111)表面共有4类对称吸附位,分别为fcc位、hcp位、top位和bridge位。通过计算表明单一H原子仅能吸附在表面top位和fcc位,当H原子在hcp和bridge位时会自动迁移到最近邻fcc位。对于H原子在材料内部的溶解,本节共研究了Al(111)层状表面的5种间隙溶解位,如图2所示,分别为表面与亚表面之间的两类四面体间隙位和一类八面体间隙位;块体材料内部的四面体和八面体间隙位。
图3a和3b为H原子在晶界∑5(100)/36.87°不同溶解间隙位的迁移路径和Al原子空位的位置,其中I3GB为靠近晶界的晶内溶解位,I4-1GB和I4-2GB为等效最优溶解位。本节选取了两条扩散路径,分别为I1GB→I4-1GB和I5GB→I4-1GB。由图3c和3d,对于互相垂直的两条迁移路径I1GB→I4-1GB和I5GB→I4-1GB,Al原子空位的存在并未降低其扩散能垒,而是大幅度的提高了扩散能垒。当不存在Al原子空位时,I1GB→I4-1GB的迁移能垒为12.96 kJ/mol。Al原子空位的存在使其迁移能垒提高到76.41 kJ/mol,能垒大幅度升高63.45 kJ/mol。对于I5GB→I4-1GB的迁移路径,无空位存在时的能垒为9.31 kJ/mol,空位的出现使其能垒降低到3.55 kJ/mol,说明Al空位促进H原子沿该路径的迁移。由以上研究可知,Al原子空位的存在对H原子在晶界的迁移具有很大的影响,Al原子空位能够促进晶内的H原子迁移进入晶界;Al原子空位对晶界内H原子迁移的作用具有方向性,在某些方向能够促进H原子的迁移,而在某些方向却大大抑制H原子的迁移。
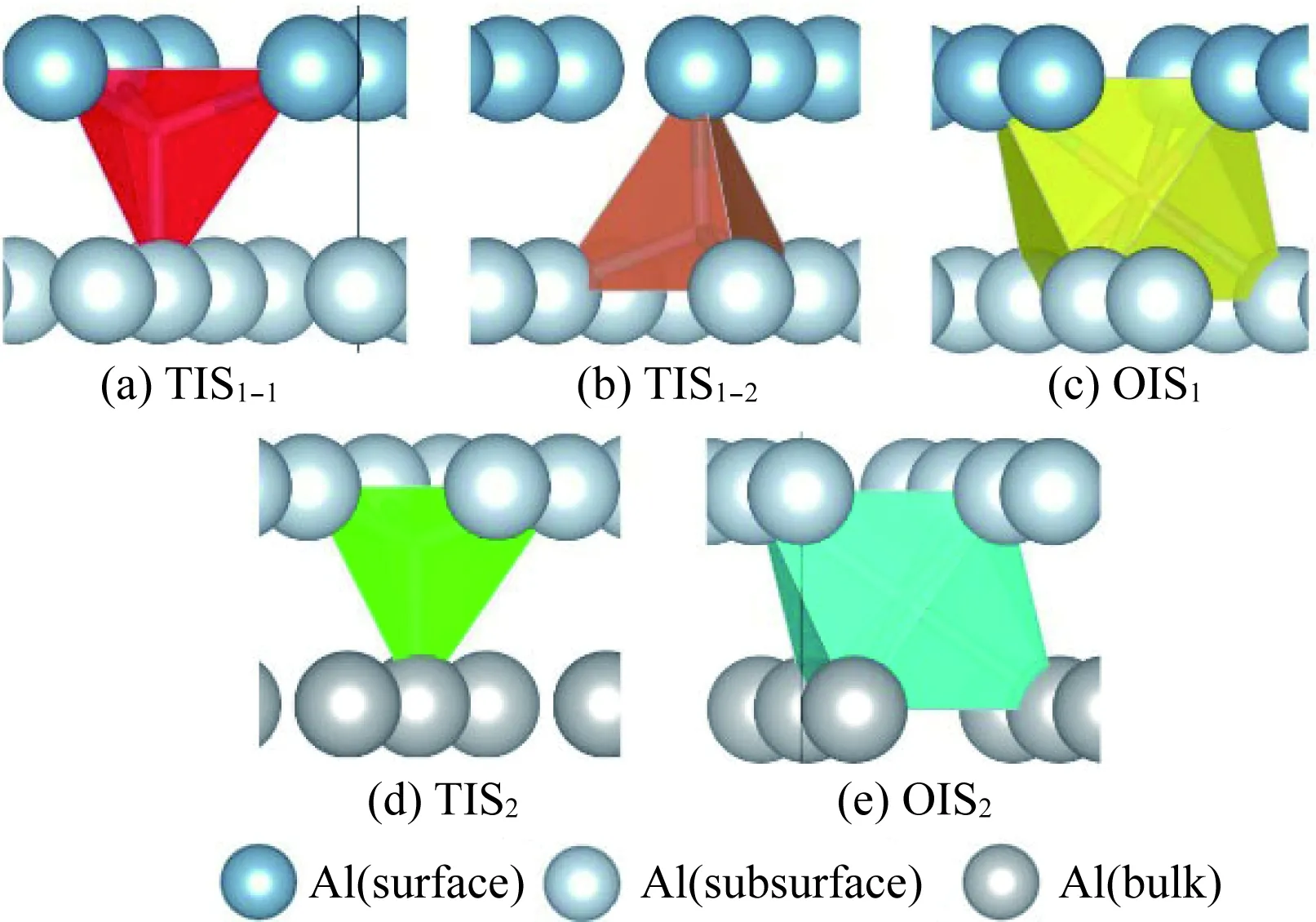
图2 H原子沿Al(111)表面吸附和向内部溶解的间隙位:(a)TIS1-1,表面与亚表面之间的第一类四面体间隙;(b)TIS1-2,表面与亚表面之间的第二类四面体间隙位;(c)OIS1,表面与亚表面之间八面体间隙位;(d)TIS2,金属Al内部四面体间隙位;(d)OIS2,金属Al内部八面体间隙位[40]Fig.2 Interstitial sites of H atom adsorbed and dissolved along Al(111) surface: (a) TIS1-1, the first type of tetrahedral interstitial site between surface and subsurface; (b) TIS1-2, the second type of tetrahedral interstitial site between surface and subsurface; (c) OIS1, octahedral interstitial site between surface and subsurface; (d) OIS2, octahedral interstitial site in Al bulk[40]
3.3 氢致铝晶间开裂行为的跨尺度计算
利用Neper软件产生多晶体结构模型,如图4所示。晶粒之间的界面利用FORTRAN语言编写的程序产生。多晶体模型包含300个晶粒,1387个晶界面。线性四面体单元(ABAQUS 类型 C3D4) 被用于划分晶内部分网格, 线性三角单元(ABAQUS类型 COH3D6) 被用于划分晶界部分网格。 多晶体晶粒的取向为正交各向异性。沿x方向的10-3mm的位移边界条件被施加在右侧表面,左侧表面的节点沿x、y、z三个方向固定。
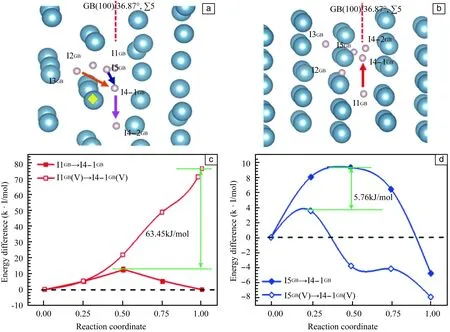
图3 H原子在晶界(100)/36.87°,∑5的溶解位示意图:(a)侧视图;(b)俯视图(其中箭头表示为不同的迁移路径,黄色四边形标记处为Al原子空位的位置)。H原子在铝晶界间隙位扩散的路径:(c)原子在有无空位情况下沿I1GB→I4-1GB的迁移路径;(d)H原子在有无空位情况下沿I5GB→I4-1GB的迁移路径(绿色箭头表示的数值为有无空位情况下迁移能垒的差值)Fig.3 Dissolved sites of H atom in (100)/36.87°,∑5 interface: (a) side view; (b) top view; (c) migration path of H atom along I1GB→I4-1GB with and without vacancies; (d) migration path of H atom along I5GB→I4-1GB with and without vacancies. Green arrows represent the difference values between migration energy barrier with vacancies and without vacancies
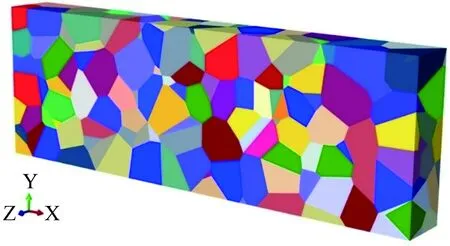
图4 多晶体模型图Fig.4 Polycrystal model diagram
利用第一性计算原理方法研究晶界偏聚对晶界强度的影响,将不同浓度H原子置于Al∑5 [100]/36.87°晶界超胞稳定吸附位,计算其晶界结合能,表明晶界结合能随H浓度升高而线性降低,如图5所示,即晶界强度线性降低。H原子对晶界的弱化效应归因于原子H的存在弱化了晶界处Al原子之间的金属键。
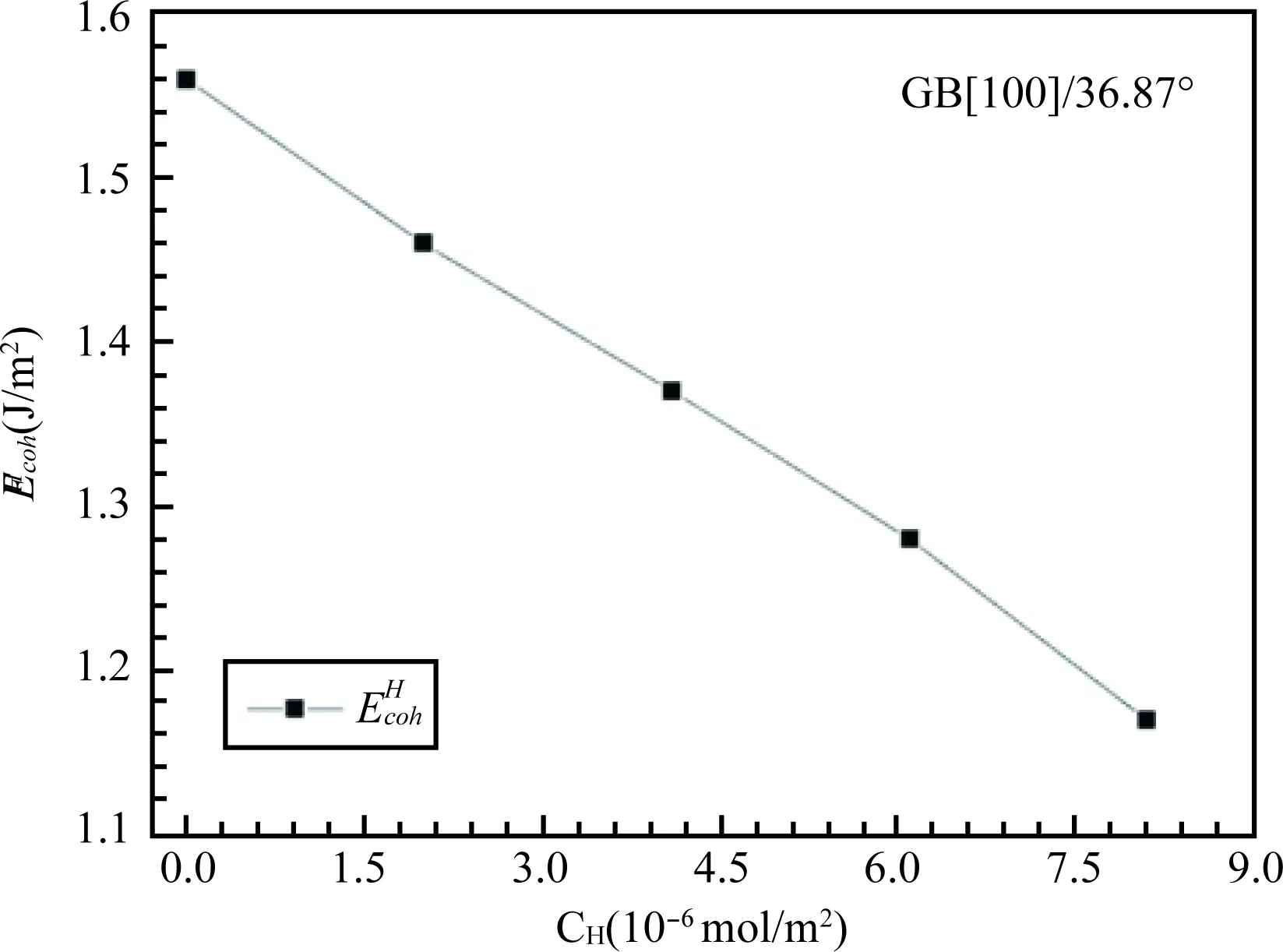
图5 Al∑5 [100]/36.87°晶界结合能随H浓度增加的变化Fig.5 The relationship between H concentration and cohesive energy of Al GB ∑5 [100]/36.87°
当一定量的H原子从环境中进入材料内部,H原子能够偏聚在晶界,导致原子之间结合力降低,这是铝合金失效的主要原因之一;虽然局部晶界应变已能够通过实验测试获得,但应力的分布仍然难以测得,内聚力有限元方法能够对晶界的应力应变分布和损伤行为进行细致的计算与模拟,其中最重要的输入参数—晶界结合能,能够通过第一性原理计算获得。通过内聚有限单元法对铝多晶体模型的晶间开裂行为进行模拟,其中利用第一性原理计算得到的晶界结合能将作为断裂能这一参数输入到内聚有限元计算中,实现原子尺度与宏观尺度之间的衔接,从而实现跨尺度计算。图6为晶界单元的损伤云图,可以看出,随着晶界结合能的降低,失效单元增多,随着失效单元的累积使得微观晶间出现微观裂纹。
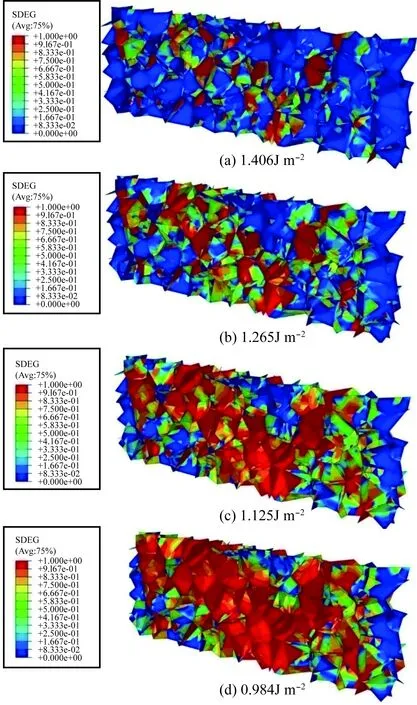
图6 不同晶界结合能下内聚有限单元法计算得到的SDEG损伤分布云图[40]Fig.6 SDEG damage distribution diagrams of polycrystal model with different binding energy of grain boundary via cohesion finite element method[40]
4 结 语
本文对计算模拟方法在金属腐蚀研究中的应用与进展进行了综述,将第一性原理与有限元计算相结合,建立了从原子尺度到宏观尺度的跨尺度计算方法。本文以铝及铝合金为例,利用第一性原理计算了Cl与表面钝化膜的相互作用来研究钝化膜的点蚀机理。本文还建立了Al-H体系,研究了H原子在Al表面和内部的吸附、溶解,扩散与偏聚,并计算H原子偏聚对晶界强度的影响。最后将原子尺度第一性原理计算获得的能量输入到宏观尺度的有限元计算之中模拟开裂行为。本研究基本完成铝大气腐蚀行为与机理的跨尺度计算与模拟框架的搭建,此方法适用于服役于大气环境中具有Cl-点蚀敏感性和氢脆敏感性的结构材料,对工程应用具有指导作用。
本课题组在后续的工作中还针对金属钝化膜的性能开展了大量的研究,利用第一性原理与电化学测试相结合的方法研究钝化膜的稳定性[41,42]及其半导体性质对其耐蚀性能的影响。
References
[1] Xiao Jimei(肖纪美), Cao Chunan(曹楚南).PrinciplesofMaterialCorrosion(材料腐蚀学原理)[M]. Beijing: Chemical Industry Press, 2002.
[2] Zhu X, Zi G.Construction&BuildingMaterials[J], 2017, 137: 330-344.
[3] Maulana A, Dipoyono H K, Khairurrijal K.IndonesianJournalofPhysics[J], 2015, 18(1): 5-9.
[4] Wang H, Han E H.ElectrochimicaActa[J], 2013, 90(5): 128-134.
[5] Laycock N J, Krouse D P, Hendy S C,etal.ElectrochemicalSocietyInterface[J], 2014, 23(4): 65-71.
[6] Wang H T, Han E H.Materials&Corrosion[J], 2015, 66(9): 925-930.
[7] Harrison T J, Crawford B R, Brandt M,etal.ComputationalMaterialsScience[J], 2014, 84(1): 74-82.
[8] Li Q K, Zhang Y, Shi S Q,etal.MaterialsLetters[J], 2012, 56(6): 927-932.
[10] Zhang G A, Zeng L, Huang H L,etal.CorrosionScience[J], 2013, 77: 334-341.
[11] Liu Zhixiao(刘智骁).TransactionsofNonferrousMetalsSocietyofChina(中国有色金属学报)[J], 2013, 23(4): 1160-1167.
[12] Pan Changchang(潘昌昌). Dissertation for Master[D]. Lanzhou:University of Lanzhou Technology, 2016.
[13] Venkatraman M S, Cole I S, Emmanuel B.ElectrochimicaActa[J], 2011, 56(20): 7171-7179.
[14] Indira K, Nishimura T.JournalofMaterialsEngineering&Performance[J], 2016, 25(10): 1-14.
[15] Giner I, Keller A.CorrosionScience[J], 2015, 100: 496-503.
[16] Ceylan S, Sergiy B, Martin S,etal.CorrosionScience[J], 2012, 58(5): 307-314.
[17] Di Stefano D, Mrovec M, Elsässer C.ActaMaterialia[J], 2015, 98: 306-312.
[18] Kulkova S E, Kulkov S S, Bakulin A V,etal.InternationalJournalofHydrogenEnergy[J], 2012, 37(8): 6666-6673.
[19] Hohenberg P, Kohn W.PhysicalReview[J], 1964, 136:B864-B871.
[20] Kohn W, Sham L J.PhysicalReview[J], 1965, 140(4A): A1133-A1138.
[21] Perdew J P, Burke K, Ernzerhof M.PhysicalReviewLetters[J], 1996, 77(18): 3865-3868.
[22] Wei Xin, Dong Chaofang, Chen Zhanghuaetal.TransactionsofNonferrousMetalsSocietyofChina[J], 2015, 25: 4102-4109.
[23] Guo F Y, Long C G, Zhang J,etal.AppliedSurfaceScience[J], 2015, 324: 584-589.
[24] Carrasco J, Hodgson A, Michaelides A.NatureMaterials[J], 2012, 11(8): 667-674.
[26] Tonigold K, Gross A.JournalofComputationalChemistry[J], 2012, 33(6): 695-701.
[27] Wei X, Dong C F, Chen Z H,etal.RSCAdvances[J], 2016, 6:79836-79843.
[28] Wei X, Dong C F, Chen Z H,etal.RSCAdvances[J], 2016, 6: 56303-56312.
[29] Digne M, Sautet P, Raybaud P,etal.JournalofCatalysis[J], 2012, 226(1): 54-68.
[30] Wei X, Dong C, Chen Z,etal.AppliedSurfaceScience[J], 2015, 355(15): 429-435.
[31] Fernandez N, Ferro Y, Kato D.ActaMaterialia[J], 2015, 94(1): 307-318.
[32] Kristinsdóttir L, Skúlason E.SurfaceScience[J], 2012, 606:1400-1404.
[33] Ferrin P, Kandoi S, Nilekar A U,etal.SurfaceScience, 2012, 606(7-8): 679-689.
[34] Mao W, Chikada T, Suzuki A,etal.JournalofNuclearMaterials[J], 2014, 455(1): 360-365.
[35] Simonovski I, Cizelj L.EngineeringFractureMechanics[J], 2013, 110: 364-377.
[36] Zhu L K, Yan Y, Qiao L J,etal.CorrosionScience[J], 2013, 77(77): 360-368.
[37] Pouillier E, Gourgues A F, Tanguy D,etal.InternationalJournalofPlasticity[J], 2012, 34(34): 139-153.
[38] Lu Xinzheng(陆新征), Lin Xuchuan(林旭川), Ye Lieping(叶列平).JournalofHuazhongUniversityofScienceandTechnology(华中科技大学学报)[J], 2008, 25(4): 76-79.
[39] Guo Yafang(郭雅芳), Wang Chongyu(王崇愚).MaterialsReview(材料导报)[J],2001,15(7):9-11.
[40] Wei X, Dong C F, Chen Z H,etal.RSCAdvances[J], 2016, 6:27282-27292.
[41] Xu A N, Dong C F, Wei X,etal.ElectrochemistryCommunications[J], 2016, 68: 62-66.
[42] Kong D C, Xu A N, Dong C F,etal.CorrosionScience[J], 2017, 116: 34-43.
