基于无迹卡尔曼滤波的高纬度超视距目标跟踪方法

2018-03-02孙永侃张萍萍

火力与指挥控制 2018年1期

孙永侃，张萍萍

（海军大连舰艇学院，辽宁大连 116018）

0 引言

单平台、单传感器在复杂海战场环境感知中缺乏全天候、高空间覆盖范围、隐身等功能［1］，与其他海域相比，北冰洋海域覆盖的大面积浮冰限制了水面舰艇的活动范围，因此，需要来自包括岸基雷达、友邻舰、舰载直升机、预警机等非本舰的第三方超视距引导信息来协助对目标位置进行精确定位与跟踪，才能保证水面舰艇极区全区域的战场感知能力。

超视距目标指示系统的传统做法是将目标的位置信息转换到以融合中心为原点的平面直角坐标系中［2］，由于超视距目标的探测距离是目标与舰艇的大地弧线长，因此，若仍然通过以雷达位置为原点的直角坐标系来标定目标的位置将不再适合。相关文献对提高超视距目标指示精度提出了各自的看法与解决方法［3-4］，但这些研究没有考虑极区特殊的地理环境对超视距目标指示的影响，没有考虑传统超视距目标跟踪方法在极区的使用缺陷，因此，要满足极区舰艇作战指挥需求，必须寻求合适的解决方法来提高极区超视距目标跟踪精度。

由于在极区（特别是近极点地区）地理北不易作为方位基准，本文提出建立横向坐标系，在极区采用横向地球坐标来表示位置坐标，采用横向地理北作为方位基准，采用横向方位角（即目标方位线与横向地理北的夹角）来表示目标方位，并根据由此而产生的目标运动模型与观测模型的非线性，提出将无迹卡尔曼滤波用于极区超视距目标跟踪，从而提高极区超视距目标跟踪精度。

1 构建横向坐标系与横向地球大地主题解算模型

1.1 横向坐标系的建立

传统地理位置的表示采用经纬度方式［5］，依据传统经纬度建立的地球坐标系和地理坐标系如图1所示，由于极区特殊的地理位置，这种表示方式导致经线收敛于两极，本文提出建立虚拟的经纬网格系统，将虚拟的经纬网格中的经度、纬度分别定义为横向经度、横向纬度，定义横向极点位于90°E/90°W子午线与赤道的交点处，定义横向赤道位于0°经线和180°经线上，定义横向本初子午线为经过北极点的90°E/90°W子午线。在此基础上确定横向极轴、横向赤道平面、横向本初子午面以及横向经纬网格，从而将地球极区转变为虚拟的横向赤道地区。

依据横向经纬网格建立横向地球坐标系。为了便于计算，将地球坐标系的Xe轴旋转至Ze轴，Ze轴旋转至Ye轴，Ye轴旋转至Xe轴，即可得到横向地球坐标系，如图2所示。

依据横向地球坐标系建立横向地理坐标系。首先对坐标系作如下定义：设地球坐标系OeXeYeZe为e系；横向地球坐标系OeXTeYTeZTe为Te系；地理坐标系OtXtYtZt为t系；横向地理坐标系OtXTtYTtZTt为Tt系；纬度为φ；经度为λ；横向纬度为φT；横向经度为λT；地球半径为R（假设地球为球体）。横向地理坐标系的原点仍定义为地理坐标系中的载体质心Ot，横向地理坐标系的北定义为沿当地横向经线指向横向北极点的方向，YTt轴指向横向北，ZTt轴沿地理垂线指向上，XTt轴的方向与YTt轴呈右手定则关系，这样就建立了横向地理坐标系，如图2所示。

1.2 构建位置变换模型

为得到两种经纬度之间的变换关系，下面建立横向地球坐标系与地球坐标系之间的变换关系。

建立横向地球坐标系后，由图3所示，由两者的旋转关系即可建立两者之间的变换关系如下：

即：

由上式即可解算出目标在两坐标系之间的位置变换关系。

假设已知目标在地球坐标系中的经纬度位置信息，则目标所在点M在横向地球坐标系中的位置计算公式为：

其中，上式仅为主值关系，具体转换时，应考虑反三角函数的主值域与横向经纬度定义域来确定真值。

假设已知目标在横向地球坐标系中的横向经纬度位置信息，则目标所在点M在地球坐标系中的位置计算公式为：

1.3 构建横向地球大地主题解算模型

传统超视距目标跟踪中，需要将目标的大地极坐标转换到以融合中为原点的直角坐标系中，为了提高高纬度超视距目标跟踪精度，本文提出将目标的大地极坐标转换到前面建立的横向地球坐标系中，下面对横向地球大地主题解算的正解与反解公式进行求解。

由图4所示，在圆球面上有两点P（1，φT1）、P（2，φT2），P1与 P2之间的大圆弧长为 S12，两点间的横向方位角 A'12、A'21，Δ为 P1、P2之间的横向经差，P点为横向极点，P、P1和P2三点组成了横极球面三角形。

向地球大地主题解算反解公式为：

2 构建超视距目标运动模型

在超视距目标跟踪中，由于地球曲率的影响，基于直角坐标建立目标的状态方程和观测方程不再合适。针对这一问题，将传感器测量的目标的大地弧长距离以及方位角转化为目标的横向经纬度表示后，本文提出进一步依据横向地球坐标系建立目标的运动状态方程和观测方程。

建立目标的运动模型是目标跟踪的一个重要环节，当目标跟踪系统以预测方式跟踪机动目标时会存在很多困难，其基本问题是所建立的目标动力学模型很难准确地反映实际目标的动力学特征。对于动态目标，其运动状态一般是未知的，且目标运动的背景也可能是比较复杂的，在对系统状态进行估计时，要求定义数学模型来描述系统状态当前时刻与以前时刻之间的关系，通常采用Singer机动模型（以匀速或者加速运动作为目标运动模型）来建立卡尔曼滤波模型。Singer机动模型用有色噪声描述机动加速度，但其机动加速度均值为零，在目标作大机动运动时，跟踪误差将会很大［6］。通常对于舰艇类大质量动目标的机动跟踪的基础是对匀速直线运动方式和匀速慢转弯运动机动方式的跟踪，因此，本文使用CT模型来描述目标运动。

假设采样时间间隔为T，令k时刻横向地球坐标系下的目标状态向量为，其中，、φT为k时刻目标的横向经度和横向纬度，v为k时刻目标运动速度，ψT为k时刻目标运动的横向航向角，ω为k时刻目标运动角速度。

则横向地球坐标系下的目标运动方程如下：

其中：设 W（k）为均值为 0、协方差为 Q（k）的高斯噪声序列；f（X（k），k）为

3 构建基于横向地球坐标系的极区超视距目标观测模型

3.1 本舰舰载超视距雷达进行目标观测情况下的目标观测模型建立

由于超视距探测距离较远，就必须考虑地球曲率的影响，因此，舰载超视距雷达对目标的探测距离不再是传统的直线距离，而是目标与雷达之间的大地弧线距离。也就是说，雷达k时刻的目标观测向量为：

观测方程为：

其中：设 v［k］为均值为 0、协方差为 R（k）的高斯噪声序列；

式中，设A'rm为目标方位，Srm为目标距离。

3.2 第三方引导信息进行目标观测情况下的目标观测模型建立

通过数据链进行第三方引导信息的远程目标指示与跟踪。数据链目标指示的内容有两种情况：

1）第三方仅提供包括经度和纬度的目标位置信息，但不提供目标运动参数。

2）第三方既提供包括经度和纬度的目标位置信息，也提供包括航向和航速的目标运动信息。

下面对这两种情况分别进行研究。

3.2.1 第三方仅提供目标位置参数情况下的目标观测模型构建

由于第三方仅能提供目标位置参数的经度纬度，因此，观测向量为：

观测方程为：

其中：设 V［k］为均值为 0、协方差为 R（k）的高斯噪声序列；

则观测向量Z［k］与状态向量X［k］的函数关系h（X（k），k）可以通过横向经纬度与经纬度之间的变换得到如下：

3.2.2 第三方提供目标位置及运动参数情况下的目标观测模型构建

由于第三方可提供目标的经纬度、速度以及航向信息，则观测向量可设置为：

则观测量Z［k］与状态向量X［k］的函数关系h（X（k），k）可以通过横向经纬度与经纬度之间的变换得出式（26）：

4 构建基于无迹卡尔曼滤波的极区超视距目标跟踪模型

4.1 目标跟踪中的非线性滤波算法分析

由前文建立的模型可见，与传统直角坐标系下的滤波不同，横向地球坐标系下，目标的状态方程以及观测方程都是复杂的非线性方程，由于目标运动本身和目标量测的非线性特性，导致目标跟踪系统总是存在不同程度的非线性。此外系统中通常还存在高斯或者非高斯的随机动态干扰，系统模型难以采用线性微分方程或者线性差分方程进行准确描述。尽管在某些情况下，当系统的非线性程度较弱，采用线性最优估计算法也能取得比较满意的效果，但这种情况在实际应用中非常少。当系统的非线性程度增大，线性最优估计算法将不能再满足实际所需要的估计精度［7-10］。

超视距目标指示系统中采用的传统扩展卡尔曼滤波算法只适用于弱非线性系统，无法实现对非线性方程的雅可比矩阵求导，线性化误差大，从而容易导致跟踪误差很大甚至发散的现象［11-15］。因此，不适用于本文建立的非线性模型的滤波。

无迹卡尔曼滤波（UKF）以UT变换为基础，采用卡尔曼线性滤波框架，通过设计少量的σ点，经过非线性函数映射，计算出随机向量统计特性（均值和方差）的传播。对线性模型，UKF具有EKF算法同样的滤波精度，但对于非线性模型，UKF变换能够更准确地估计非线性函数的均值和方差，不需要计算模型的雅克比矩阵，避免了对非线性模型的线性化处理及坐标转换带来的误差，并且由于UT变换比求导雅可比矩阵能更好地描述非线性特性，因此，比扩展卡尔曼滤波有更高的估值精度［16-21］。

本文针对基于横向地球坐标系的目标状态方程和观测方程的非线性特性，提出将无迹卡尔曼滤波方法运用到横向地球坐标系下的超视距目标跟踪。

4.2 构建UT变换模型

将它们的均值和方差经过加权处理，应用于采样的每个 Sigma点，得到 y的统计特性（，Py）

4.3 构建无迹卡尔曼滤波模型

步骤1，选定滤波初值：

对 k=1，2，3…执行：

步骤2，计算k-1时刻的2n+1个Sigma样本点

步骤3，计算k时刻的一步预测模型值

步骤4，计算k时刻的一步预测样本点

式中

步骤6，计算增益矩阵

步骤7，计算滤波值

5 仿真与分析

仿真条件设置如下：

假设目标初始经纬度为（100°，78°），即初始横向经纬度为（-2.113 8°，11.815°），初始横向航向为38.869 8°。如表1所示，目标首先作匀速直线运动，然后直线加速又直线减速，紧接着，目标以恒定速率作蛇行机动，然后，目标再作直线加速，最后以一恒定速率匀速直线运动。

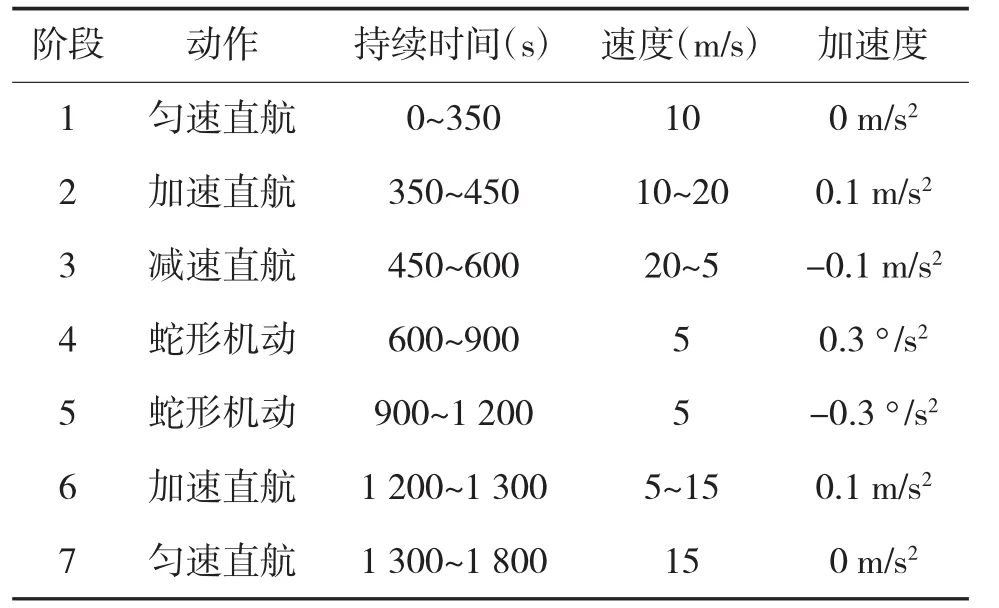
表1 目标运动轨迹

假设仿真实验目标运动的初始状态值为X（0）=［-2.113 8°，11.815°，10，36.87°，0］T、P（0）=diag（10-6，10-6，100，100，1），系统噪声阵为 Q（k）=diag（10-8，10-8，1，1，0.01）。目标运动轨迹如图5所示，目标速度变化曲线如图6所示。

根据前文构建的基于横向地球坐标的极区超视距目标运动模型和观测模型，采用UFK算法进行滤波，UKF 参数设置：（α=0.01，β=2，k=0）滤波采样间隔T=10 s，并分别对采用本舰舰载超视距雷达进行目标观测及采用第三方引导信息进行目标观测两种情况进行了仿真实验。

1）采用本舰舰载超视距雷达进行目标观测的目标跟踪仿真。

为了仿真方便假设本舰不动，本舰超视距雷达所在位置经纬度为（90°，80.3°），即横向经纬度为（-1.531 7°，9.579 4°）。雷达探测的方位误差为 0.1°，距离误差为0.1 km。观测噪声为R（k）=diag（0.01，0.01），采用UKF算法进行滤波，得到位置估计与目标的真实运动轨迹的比较结果如图7所示，并进行50次蒙特卡罗（Monte Carlo）仿真得到各测量时刻的位置均方根误差，如下页图8所示。

2）第三方通过数据链进行远程目标指示的目标跟踪情况。

首先对第三方仅提供目标位置（经纬度）的情况进行仿真如下：

然后对第三方可提供目标位置（经纬度）、速度、航向的情况进行仿真如下：

假设位置误差为1 n mile，速度误差0.1 kn，航向误差0.1°。则观测噪声为采用UKF算法进行滤波，将得到的位置估计与目标的真实运动轨迹的比较结果如图11所示，并进行50次蒙特卡罗（Monte Carlo）仿真得到各测量时刻的位置均方根误差，如图12所示。

从图7～图12可以看出，UKF滤波对目标位置跟踪的效果是非常好的。初始状态下，滤波曲线能很快收敛到真实航迹附近，跟踪曲线也比较平稳。由图9～图12可以看出，当第三方引导时，增加目标速度和航向观测信息时，比仅提供位置进行观测的跟踪效果好。仿真分析的结果表明：基于横向地球坐标系的极区超视距引导中的目标跟踪模型，避免了坐标系间的多次转换，提高了目指信息的精度。

6 结论

针对传统超视距目标指示中将目标的位置信息转换到以融合中心为原点的平面直角坐标系中进行目标指示所引入的目指信息偏差问题，提出将横向地球坐标系引入极区超视距目标指示系统中，将目标位置用唯一的一组横向地球坐标来描述。通过构建基于横向地球坐标系的大地主题解算模型，将目标的位置信息转换到横向地球坐标系中，进一步建立基于横向地球坐标系的目标运动模型和目标观测模型，并针对由此产生的目标状态方程和观测方程的非线性特性，提出基于无迹卡尔曼滤波的滤波模型，仿真分析的结果表明，该模型有效提高了超视距目标跟踪精度，能够有效满足极区舰艇作战指挥需求。

［1］朱士龙，张佳忠，顾浩.超视距目标信息仿真测试技术研究［J］.系统仿真学报，2004，16（8）：1701-1704.

［2］王钢，贾世楼，张琦.超视距目标指示的方法与性能研究［J］.哈尔滨理工大学学报，2006，11（6）：110-113.

［3］卢江涛，段立，罗兵.大地坐标系的超视距目标指示系统［J］.火力与指挥控制，2008，33（10）：81-84.

［4］吴云桥，耿伯英，段立.基于大地坐标的对空超视距目标跟踪研究［J］.电光与控制，2009，16（8）：40-43.

［5］赵建军，陈滨，杨利斌.基于四元数的大地坐标转换算法及实现［J］.计算机工程与应用，2013，49（4）：202-205.

［6］孙晏涛.水面舰艇运动仿真模型研究［J］.舰船电子工程，2011，204（6）：118-121.

［7］曹鹏.基于IMM-UKF运动目标跟踪系统研究［D］.沈阳：沈阳工业大学，2012.

［8］江宝安.基于UKF滤波的单目标跟踪算法研究［D］.长沙：国防科学技术大学，2003.

［9］苏畅.UKF在水中目标跟踪系统中的应用［D］.哈尔滨：哈尔滨工程大学，2009.

［10］胡正兵，夏佩伦.基于UKF的潜艇机动目标跟踪［J］.舰船电子工程，2010，30（9）：74-76.

［11］石勇，韩崇昭.自适应UKF算法在目标跟踪中的应用［J］.自动化学报，2011，37（6）：755-759.

［12］张苗辉，杨一平，刘先省.基于UKF的机动目标跟踪算法［J］.火力与指挥控制，2007，32（8）：37-39.