基于PDF-CDF的随船备件优化配置方法*

李志强，徐廷学，董 琪，曾 翔，刘玉东

（1.海军航空大学，山东 烟台 264001；2.解放军95080部队，广东 汕头 515000）

0 引言

备品备件是装备在使用与维修过程中所需的易损件、元器件、部组件以及专用工具的统称。在舰艇备品备件配置和管理的过程中，任何一个环节缺失或运转不正常，将直接影响舰艇装备的战备完好性，为部队训练、作战等任务的顺利完成带来隐患。随着舰艇装备的跨越式发展，新型舰艇装备在复杂程度、集成化程度、信息化程度等方面都大幅提高，对现行的备品备件配置和管理手段、方法提出了新的、更高的要求。

随船备品备件的传统配置方法不够科学，主要体现为：1）备品备件的配置种类和数量与舰艇实际消耗不匹配，存在着部分设备使用强度小但备件配备种类和数量较多，而部分设备使用强度大、备件消耗量大但配备数量较少的现象；2）标准件、通用件重复配置，导致一些标准件和通用件在舰船上被大量储存，加大了使用中的管理难度，占用了有限的备件舱室空间。

据统计，在过去的3年时间里，某型舰船使用的备品备件只占22%，即有78%的多余携带量。在2～6周的巡航时间里，舰船配置的随船备品备件几乎没有消耗，当巡航时间延长至12～15周时，携行的备品备件数量将成倍增加。大批的随船备品备件增加了舰船的运行负荷，占用了有限的武器装备储存空间，压缩了舰艇人员的活动范围。

1 随船备件优化配置研究现状

在故障发生之前，舰船上的备品备件可能已经在舱室里存放了多年，这对于追求“经济可承受性”的敏捷保障而言，备件储存效率非常低下。关于美军海岸警卫队的审计报告指出［1］，某型舰船清理了价值高到490万美元的备品备件，而该舰船在20世纪60年代建造花了1 600万美元，在20世纪90年代进行寿命周期大修花了5 500万美元，这就意味着，该型舰船在巡航期间多配置了约占总价值7%的备品备件。

鉴于此，外军开展了大量优化随船备品备件配置的研究：Moon等［2-3］针对随船备品备件消耗呈现不稳定性、间歇性等特点，提出了将直接预测方法与层次预测方法相结合的优化算法，并结合多元需求特点构建了回归分析模型；针对装备可靠性数据获取困难、器材逐一仿真任务量大等问题，Jaarsveld等［4］提出了用于计算相对贵重备件的简单算法模型，减少了装备器材逐项仿真计算的工作量；Barabadi等［5］人克服以往从经费、空间、重量等约束条件下建模的不足，根据运行环境、维修策略、操作技能等因素提出了基于可靠性指标的备件预测优化模型。几乎与此同时，针对随船备件配置问题，我军依托军事院校与地方高校做了大量相关工作：阮旻智等［6］针对随船备件多级维修供应保障模式下配置算法效率低的问题，引入分层优化的思想对算法进行改进；针对表决系统确定随船备件存在模型复杂、计算不精确的问题，刘任洋等［7］提出了利用R-等效转化方法进行寿命分布等效的随船备件需求预测方法；以舰船远海航行为背景，蔡芝明等［8-9］以载荷、费用、排水量、舱室空间等为约束，运用拉格朗日乘子法构建了随船备件库存模型，并借助系统资源约束因子、动态调整法对混合约束条件下的算法进一步优化。

确定随船备件和消耗品储存数量有两种传统方法：第1种基于平均故障间隔时间（Mean Time Between Failure，MTBF）的配置方法，第2种基于技术人员工作经验的配置方法。业务机关关心的是维持舰船例行巡航所需备品备件的种类和数量，以及战备巡航所需的备件明细。部分随船备件的确定依赖于技术人员的经验，缺乏一个度量标准对所携备件减轻的风险进行准确量化。

近年来，多个研究所、院校构建了一系列仿真模型确定随船备品备件的优化储存策略，采用的优化方法主要有随机过程［10］、遗传算法［11］和蒙特卡洛仿真［12］3种。随机过程是最简单的方法，但在实验条件下，利用MTBF参数进行随机过程分析获得的航空备件或者车间备件配置结果无法与在海航行舰船的配置实际相提并论；遗传算法具有很强的鲁棒性、易于并行处理，可以对大样本空间进行建模，但局部搜索能力差，容易陷入局部最优，出现未成熟收敛和随机游走等现象；运用蒙特卡洛仿真方法可以进行随船备件风险分析，并可以在缺乏系统仿真的情况下实现局部仿真，有效解决备件配置初期数据缺乏的问题，但对数十万种备品备件逐一仿真数据量大，消耗巨大的计算资源。

2 随船备件优化配置方法

随船备品备件中包含消耗品和备件［13］：消耗品，即在失效/拆卸时不再加以修复的零部件；备件，即维修装备及其主要成品所需的元器件、零件、组件或部件的统称。对于消耗品而言，从开始使用直到用尽，直接进行更换，与MTBF不相关；对于备件而言，MTBF意义重大，可以确定每次巡航需要配备的备件种类与数量。因此，研究主要集中于备件，尤其是影响舰船运行安全、执行任务的关键件、重要件、易损件、常耗件等，涉及引擎、雷达、陀螺仪、空调、蒸汽设备、排污系统等设备。

为了简化模型，作出如下假设：

1）装备没有灾难性故障；

2）部件发生故障时，直接替换；

3）所有故障都是单一事件，没有故障是相关的；

4）巡航周期开始时，所有备件都是新的；

5）在整个巡航期间，所有系统和部件都会使用。

2.1 基于经验的配置方法

根据技术人员的工作经验，某型舰船备件配置数量如表1所示。

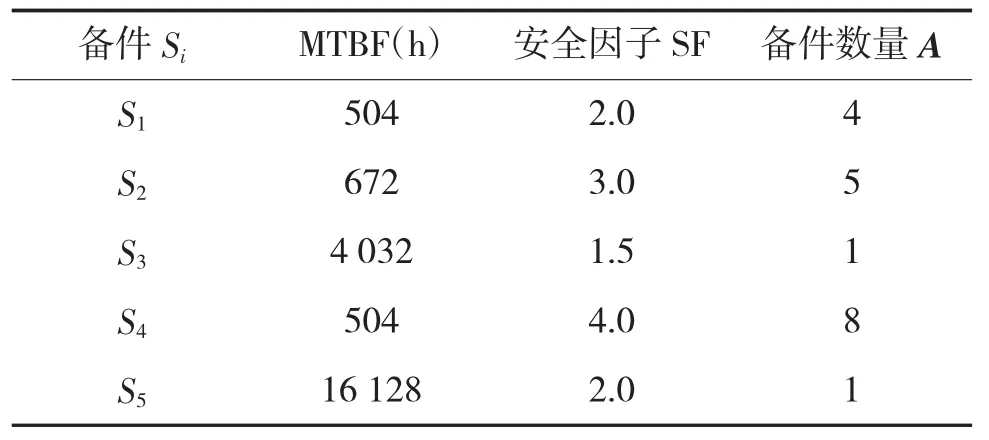
表1 给定PL3巡航时间下的备件配置矩阵A

矩阵A代表了舰船巡航时采用传统方法确定的储存备件基线。Si表示备件类别，储存数量等于巡航时间长度除以MTBF与人员安全因素的比值：

MTBF表示平均故障间隔时间，SF是指定备件分配的安全因素，tp表示巡航时间，如表2所示。

表2 巡航时间

如果技术人员感觉MTBF值不能真实地表征备件的可靠度性能，可以相应地增加舰船上储存的备件数量。

2.2 基于MTBF的配置方法

建立随船备件配置数量优化矩阵B：

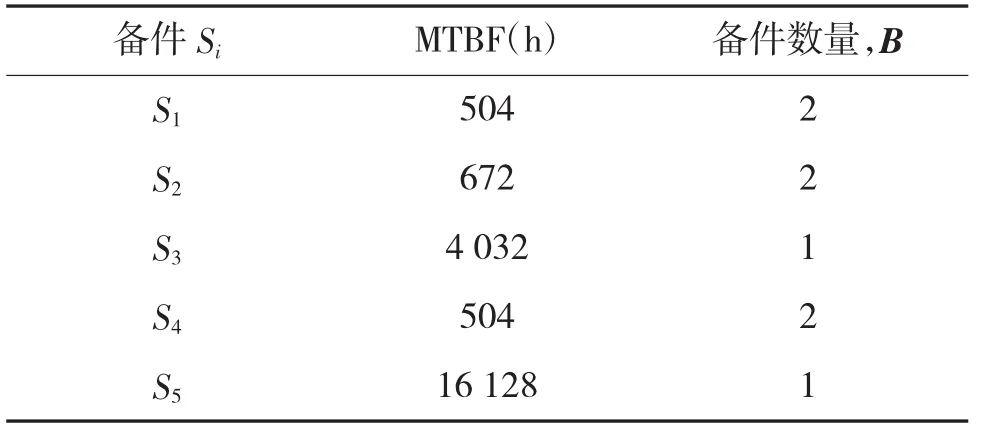
表3 给定PL3巡航时间下的备件配置矩阵B

对比式（1）可知，式（2）移除了安全因素 SF，这就确定了舰船随船备件的最小配置数量，如表3。

2.3 基于PDF-CDF的优化配置方法

确定舰船随船备件配置数量的两个矩阵已经建立，可以构建一个与下降率有关的函数，比较舰船在给定巡航时间内随船备件的库存数量。假设下降率为服从泊松分布的随机变量pi，可以用以评估给定巡航时间内失效事件的发生次数：

为了确定随船备件的优化配置数量，利用给定备件MTBF和给定巡航时间的概率密度函数（PDF）和累积分布函数（CDF）构建矩阵C。

PDF代表了在某一事件中有k个部件发生失效的概率p1，CDF代表了最多有k个部件发生失效的概率p2。从图1可以看出，PDF表示在巡航期间最多发生一次失效，而CDF表示部件将会发生3次失效。

尽管随船备件配置数量越多，舰船的战备完好性越高，但是，有限的仓储空间和购置经费决定了随船备件配置数量只能在0与基于经验配置方法的配置数量之间取值。根据舰船不同的巡航时间和相应备件的故障间隔时间确定了不同值对应的CDF曲线，大致形状如图1所示。从图中可以看出一个普遍的特点，即在累积失效率为p≈0.9时，CDF曲线的变化率发生明显变化：当p＜0.9时，曲线比较陡，k的较小增加将引起概率值的快速变化，这就意味着，少量增加储存备件的数量就可以大幅度地提高舰船的任务完成率；当p＞0.9时，曲线比较平坦，k的增加只能引起概率值的微小变化，这就意味着，此后可以降低随船备件的储存数量以满足舱室空间与购置经费等因素的约束要求。因此，将CDF曲线上p=0.9时对应的优化配置数量k定义为矩阵C90，不同巡航时间下各类备件的储存数量如下页表4所示。

3 优化配置方法验证分析

3.1 与传统配置方法对比分析

从表4可以看出，矩阵A确定的配置数量比矩阵C90确定的优化数量多，矩阵B确定的配置数量比矩阵C90确定的优化数量少。为了对应用3种方法确定的配置数量进行比较，定义EE：

对比矩阵A和矩阵C90的优化配置数量，不难发现，矩阵A通常超过矩阵C90优化数量，有大约49%的超出携带量，即每项器材大约多出3件备件。

矩阵C90确定的备件数量比矩阵B多，为了检验优化条件下备件数量的缺失，建立ED：

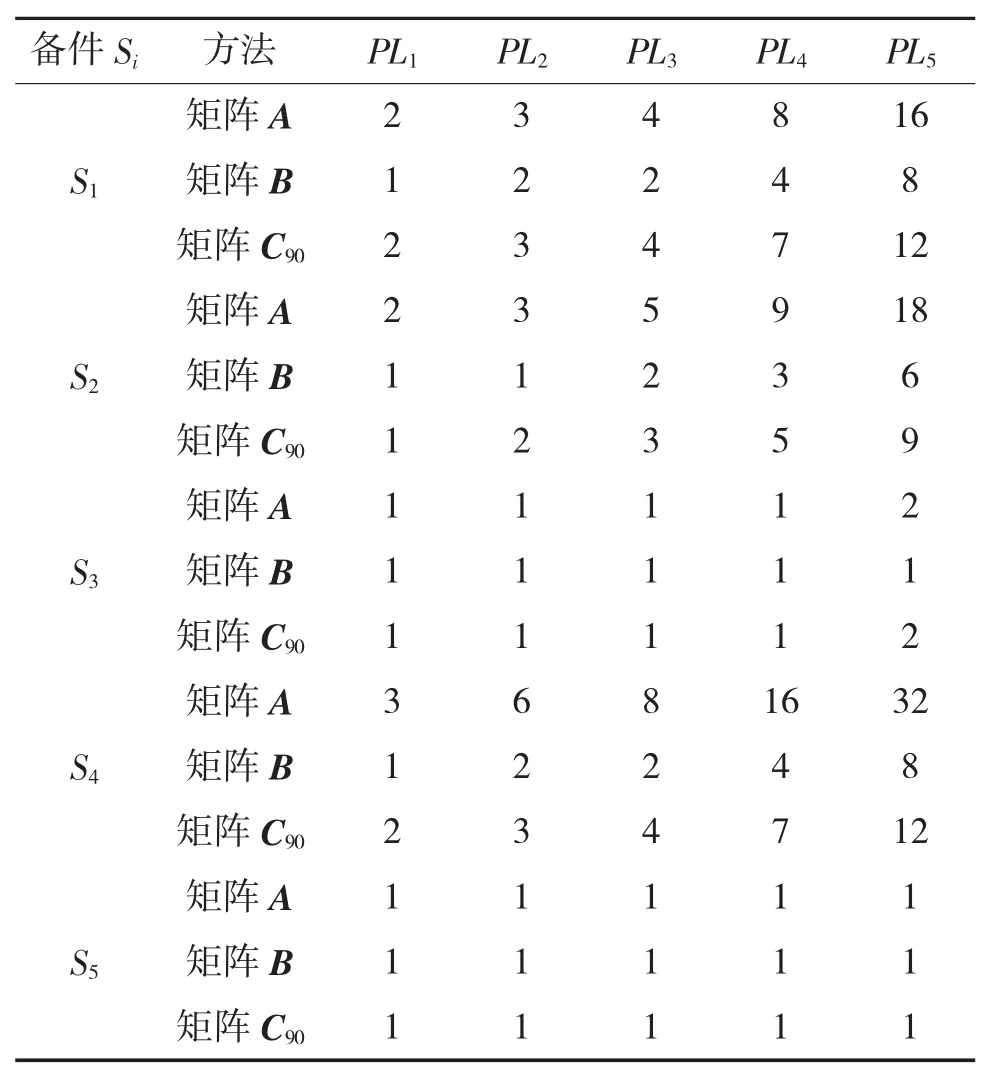
表4 不同巡航时间下的储存备件数量

对比矩阵C90和矩阵B的优化配置数量，不难发现，矩阵B的备件数量通常少于矩阵C90优化数量，大约存在31%的备件缺失，每项器材相对于优化值缺少1～2件。

对比分析表明，应用经验配置方法矩阵A确定的优化值相对于矩阵C90携带了大量多余的备件，当移除安全因素之后，得到配置数量相对缺乏的矩阵B，而此时的数量存在导致任务完成率降级的巨大风险。经考察，在5/6的试验案例中，90%的随船备件优化储存数量是有效的，结合多个不同备件的PDF-CDF曲线得到了验证。因此，可以认为矩阵C90是确定舰船随船备件优化配置值的最佳方法。

对于部分技术人员来说，优化矩阵C90确定的配置数量可能说服力不够。由于C90主要是通过作图观察确定的，现在从优化点C90往左、往右在两个方向上增加评估点C50、C99。经作图统计，对于C50确定的优化数量，相对于经验方法矩阵A有80%的平均概率造成备件缺失，相对于矩阵B的储存数量有13%的备件缺失风险，这就意味着，C50确定的储存数量对于舰船巡航任务的完成存在巨大风险。对于C99确定的储存数量，相对于经验方法矩阵A多出20%的备件储存数量，相对于矩阵B多出45%的备件储存数量，也就是说，C99确定的储存数量加大了舰船巡航时的负载量，占用了更多的舱室空间。

3.2 基于OPUS软件的仿真验证

OPUS10是由瑞典SYSTECON公司研发的综合保障软件，最新版本为OPUS10 Version 8.0，广泛用于航空航天、航海装备的备件优化与费效分析［14-15］。不同于飞机等航空装备，舰船在巡航期间远离港口、码头，船上官兵具备更换故障件的能力，不考虑其维修能力，因此，必须配备具有一定满足率的随船备件。

以某型舰船的某型雷达为例进行仿真分析。由于该型雷达具有上百种备件，限于篇幅与保密要求，选取了具有代表性的10种备件，如表5所示。根据单项备件保障概率法，可以通过式（7）确定初始备件配置方案［16］：

由于单项备件保障法确定的随船备件数可能出现总投资费用和可用度不合理等现象，运用OPUS10软件进行优化配置，详细思路与步骤请参考文献［15-16］。该型雷达备件的初始配置方案与90%、95%、98%3种满足率条件下的优化配置值见表5，各优化方案的费效分析曲线如下页图2所示。

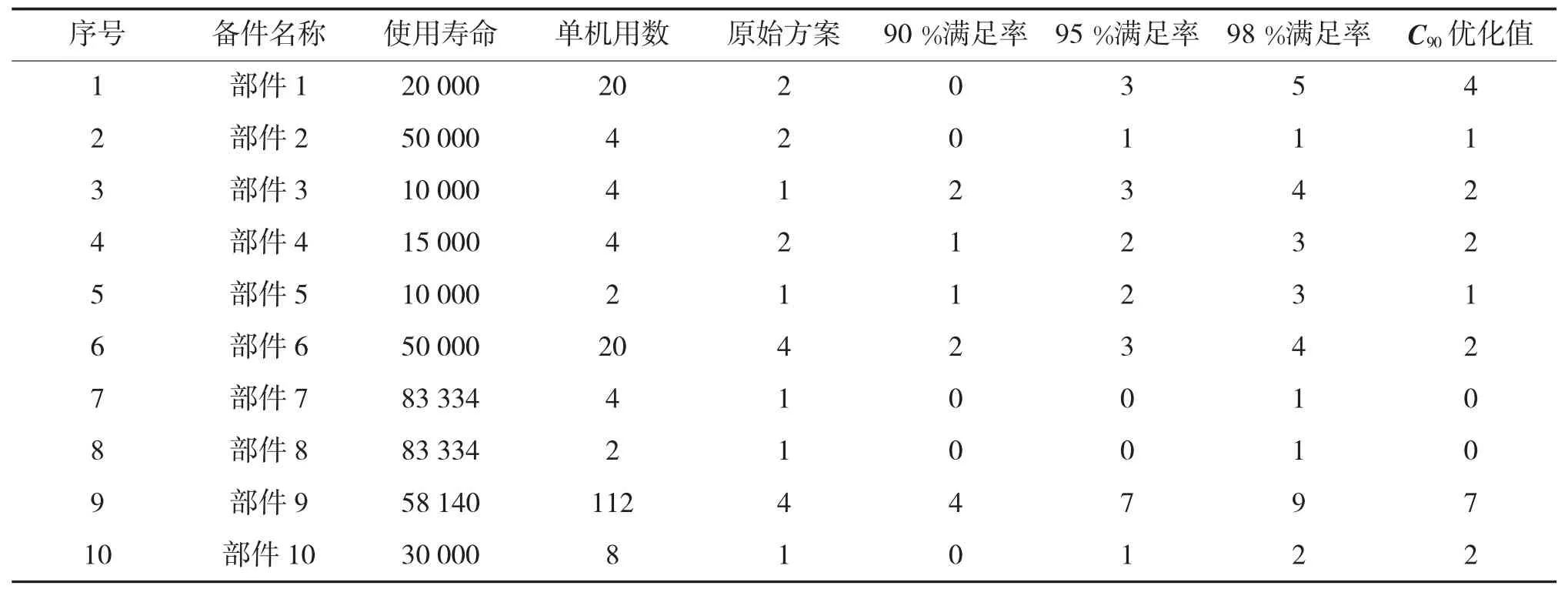
表5 不同优化配置方案下的雷达备件配置数量

根据式（3）、式（4）构建随船备件的 CDF-PDF曲线，确定C90时的优化配置数量。从表5中的优化配置值可以看出，每个备件的C90优化值介于满足率为90%与98%的优化配置数值之间，可以得出结论，C99确定的优化配置方案满足率高于90%，且费用低于98%满足率时的总投入，即C90优化配置方法科学可行。

4 结论

依靠技术人员经验的传统方法确定的随船备件配置数量，片面地提高了舰船装备的任务完成率，却降低了备件的利用率，消耗了大量的物资经费，占用了大量的储存空间，增加了舰船的排水量，降低了舰船的机动性与巡航时间。此外，过多的舰上备件储存数量为岸上舰船器材保障增加了负担，不得不加大仓库储存占用更多的土地与空间，同时，也给舰船器材的管理库存和信息化建设增加了难度。

通过验证分析，确定了舰船随船备件优化配置方法，按照此方法进行随船备件储存，同时，根据巡航实践，比如南方与北方存在地理差异、不同的巡航任务之间存在差异，对配置结果进行不断修改完善。对于部分消耗品，如果超过3年未使用，就可以建议从舰船上清理，不再配置；对于部分备件，如果超过5年未使用，也可以从舰船上清理，不再配置。备件换件时遵循一对一原则，即一项装备器材发生故障通过一次更换解决，不存在相关失效发生，不存在多米诺效应。在实际工作中，相关失效还是普遍存在的，因此，下一步将深入分析相关失效情况下的随船备件配置方案。

［1］GOSHORN J A，JR E M D，LAYTON B E.Spare part storage optimization onboard deployable military support assets［J］.Naval Engineers Journal，2010（1）：137-147.

［2］MOON S，HICKS C，SIMPSON A.The development of a hierarchical forecasting method for predicting spare parts demand in the South Korean Navy-a case study［J］.Int.J.Production Economics，2012（140）：794-802.

［3］MOON S，SIMPSON A，HICKS C.The development of a classification model for predicting the performance of forecasting methods for naval spare parts demand［J］.Int.J.Production Economics，2013（143）：449-454.

［4］JAARSVLD W V，DEKKER R.Spare parts stock control for redundant systems using reliability centered maintenance data［J］.Reliability Engineering and System Safety，2011（96）：1576-1586.

［5］BARABADI A，BARBADY J，MARKESET T.Application of reliability models with covariates in spare part prediction and optimization-a case study ［J］.Reliability Engineering and System Safety，2014（123）：1-7.

［6］阮旻智，李庆民，李承，等.改进的分层边际算法优化备件的初始配置方案［J］.兵工学报，2012，33（10）：1251-1257.

［7］刘任洋，李庆民，王慎，等.任意寿命分布单元表决系统备件需求量的解析算法［J］.系统工程与电子技术，2016，38（3）：714-718.

［8］蔡芝明，金家善，陈砚桥，等.多约束下编队随船备件配置优化方法 ［J］. 系统工程与电子技术，2015，37（4）：838-844.

［9］蔡芝明，金家善，陈砚桥.混合约束下随船备件配置优化方 法 ［J］. 北 京 航 空航天大 学 学 报 ，2015，41（12）：2340-2347.

［10］陈童，黄卓，谭林，等.考虑库存损耗的单部件系统可修备 件 需 求 模 型 ［J］.系 统 工 程 学 报 ，2012，27（2）：270-278.

［11］赵建忠，徐廷学，李海军，等.基于改进Theil不等系数的导弹备件消耗预测［J］.系统工程与电子技术，2013，35（8）：1681-1686.

［12］张永强，徐宗昌，孙寒冰，等.基于蒙特卡洛仿真和并行粒子群优化算法的携行备件优化［J］.兵工学报，2016，37（1）：122-130.

［13］任敏，陈全庆，沈震.备件供应学［M］.北京：国防工业出版社，2013.

［14］OPUS10 User’s Reference Part 1-Model Description［Z］.Sweden：Systecon AB，2009.

［15］韩光林，阮平南，杨威.基于OPUS的航空装备初始备件决策模型研究 ［J］.科学技术与工程，2014，14（1）：114-118.

［16］李田科，李伟，沙卫晓，等.备件可靠性分析及需求预测［J］.兵器装备工程学报，2016，37（4）：47-50

［17］肖波平，康锐，王乃超.民机初始备件方案的优化［J］.北京航空航天大学学报，2010，36（9）：1057-1061.