基于一致性修正的多属性大群体决策方法*

赵 谦，陈云翔

（空军工程大学装备管理与安全工程学院，西安 710051）

0 引言

在社会经济问题日益复杂的今天，往往需要不同领域的专家参与到决策问题中来，发挥不同专家的特长，集思广益。但由于专家的知识水平、能力、研究领域的不同，造成专家间偏好信息差异性较大，使得群体共识难以达成，进而造成决策效率低下，人力物力的浪费。针对这一问题，不少专家学者进行了研究，基本思想是决策者通过设定某种机制进行多轮协商，使得专家之间能够充分交流，专家不断修正自身偏好信息，提高群体的一致性，从而提高决策的科学性。文献［1］通过建立一致性指数最大化的属性权重优化模型来解决专家间偏差过大的问题；文献［2］通过全局因素和局部因素两个信息交互因素来调整专家偏好信息的修正值；文献［3］利用专家重要度对专家进行分类，对不同类的专家反馈不同的偏好信息修正矢量；文献［4］利用优化步长算法对共识度较差的专家偏好信息进行快速修正，提高群体交互的效率；文献［5］提出两种共识达成算法都以群体偏好为参照修正个体偏好，使群体共识达成；文献［6］通过反馈机制中的识别阶段和反馈调整阶段来调控达成共识；文献［7］建立谐则模型最小化认知差异，建立和则模型平衡决策者满意度关系，使决策系统螺旋推进和谐运行。

通过对现有文献的整理，主要发现以下几个问题：

1）文献中的专家权重多是由决策者主观判断得到，主观性较强，这就要求决策者有较强的能力，否则容易引起专家赋权不准确。专家权重在决策中非常重要，权重高的专家的偏好信息对决策的结果影响程度较大，往往修正较少。因此，需要科学准确地对专家赋权；

2）文献中的群体一致性修正模型多是针对专家数较少的情形，一般是3到5名专家，涉及到大群体决策问题，许多文献中模型的适用性较差。而现代社会的复杂决策问题需要多个领域的多名专家参与，因而如何对大群体决策问题中的群体一致性进行修正是迫切需要解决的问题。

基于上述分析，本文提出了一种新的群体一致性修正模型，主要的工作有：1）在专家权重未知的情况下，通过专家自身的偏好信息来挖掘专家在决策中的重要程度，并通过一个目标规划问题来获取；2）考虑到专家数目较多，引入对大群体适用性较好的花朵授粉算法并改进用来求解模型；3）结合聚类算法中属性权重调整优化聚类效果的思想，建立一个优化模型对群体一致性进行修正。

1 专家权重优化模型

1.1 问题描述

在决策问题中，由于专家的专业背景，学术水平等不同，给出的偏好信息往往差异较大，决策者很难主观判断出各个专家在决策问题中的重要程度。为了避免决策者主观判断失误引起的专家赋权不准确，本文采用客观赋权法。客观赋权法的关键在于如何通过专家给定的偏好信息挖掘出专家在决策问题中的权重大小，本文通过定义相似度和一致度两个量来对专家进行组合赋权。

1.2 模型建立

假设某一决策问题中，有m个专家针对r个方案进行择优排序，每一个方案含有n个属性。记专家集 E={Ei|i=1，2…m}，方案集 P={PR|R=1，2…r}，属性集 A={Aj|j=1，2…n}。

定义1（相似度）：相似度是指专家之间偏好信息的相似程度，相似度越大，表明专家间偏好信息的差异性越小，专家的意见越接近。某一专家的平均相似度越高，表明该专家给定的偏好信息越可信，应该赋予该专家较高的权重。

每个专家给出的偏好信息可以用空间矢量V（r×n）表示，两个专家偏好矢量 Va、Vb的相似度 Sab定义为［8］：

其中，Va表示矢量Va的行均值，|Va|表示对Va取绝对值，‖Va‖表示求Va的欧式2-范式。

对某一专家与组内所有专家的相似度求平均，即得到该专家的平均相似度：

定义2（一致度）：专家给定的偏好信息逻辑是否清晰，随机性和不确定性是否较小，反映了专家在决策中所起作用的大小。本文用一致度来表示专家给定信息的确定程度，某位专家给定的偏好信息一致度越高表明该专家给定的矛盾信息越少，则该专家的可信性越高，应该赋予该专家更高的权重。

信息熵代表了信息源的不确定性和随机性［9］，信息熵越小，表明信息的不确定性和随机性越小，故本文引用信息熵来表征专家一致度的大小，信息熵的定义为：

则专家的一致度为：

通过上文分析可知，专家的权重与专家的平均相似度、一致度都是正相关；如何表征权重与平均相似度、一致度两个量之间的相关性，本文引用文献［10］中的夹角余弦法，可得到如下表达式：

为了充分利用相似度、一致度得到专家的权重信息，本文建立了如下的最优化模型：

式中，θ∈（0，1）为一个平衡系数，表明了决策者对某一条件的重视程度，θ越大表明决策者越重视相似度对专家权重的影响，反之θ越小表明决策者越重视一致度对专家权重的影响。

1.3 模型求解

由式（7）可以看出优化模型是一种典型的带约束优化问题，为此，本文先将该模型转化为无约束优化模型，针对由式（7）的约束条件作如下处理：

简记为：

其中：

近些年，启发式仿生优化算法在许多领域的优化问题上得到了广泛的应用，并取得了较好的工程应用效果。本文选用花朵授粉算法（Flower pollination algorithm，FPA），该算法是英国剑桥大学学者Yang于2012年模拟花朵授粉过程提出的一种新型元启发式群花粉优化算法［11］。由于该算法能够较好地解决全局搜索和局部搜索平衡问题，并采用Levy飞行机制，使其具有良好的全局寻优性能，因此，被广泛应用于非线性求解［11］、多目标优化［12］、无线传感网［13］、电力系统［14］等领域。为此，本节采用花朵授粉算法对模型进行求解，其基本解算流程如下：

Step1：初始参数，设定花粉配子数量N、最大迭代次数Kmax、转换概率p等；

Step4：计算当前的全局目标函数最大值gbest，并记录对应得最优解best、wbest；

Step5：若条件（rand≤p）成立，依据式（8）、式（9）对解进行更新；否则，依据式（10）对解进行更新；

Step6：计算新解的目标函数值并与当前目标函数值进行对比，若比其大，将对当前解及目标函数值进行更新，否则，保留当前解及目标函数值；

Step7：计算全局目标函数值的最大值，并更新最优解wbest；

Step8：若满足终止条件，则输出全局最优解wbest，否则，转至 Step5。

1.4 群偏好集结

得到各个专家的权重后，通过加权求和对专家偏好信息进行集结，得到群体偏好矢量GV。

2 偏好一致性修正模型

2.1 问题描述

上文虽然对群体偏好信息进行了集结，但简单加权求和会忽略群体的差异性，这样会使这部分专家对群体集结的结果不认同，共识难以达成。解决方法是通过多轮协商，专家改进自身偏好信息，对群体一致性进行修正，尽量使群体偏好收敛。

如果把每个专家的偏好信息看作空间上的各个点，把上文中加权求和得到的群体偏好矢量看作聚类中心，要使群体决策信息收敛，用聚类的思想就是要通过某种优化规则使得聚类成员的一致性不断提高，直到聚类成员的一致性达到决策者感到满意的某个阈值。

在聚类思想中，部分学者提出了通过调节属性权重［15-18］来优化聚类一致性的问题。本文正是基于这种思想：在一次决策之后，将得到的群体偏好进行一致性修正，调整属性权重，然后反馈给各个专家并组织讨论协商，专家修改自身的偏好信息，再次进行信息集结。反复讨论直到群体的一致性达到决策者满意的某一阈值。

2.2 模型建立

定义3（一致性）：一致性是指两个空间矢量加权距离的倒数［15］，一致性越大表明空间上的两个点越接近，显然如果在决策空间上所有专家偏好矢量与群体偏好矢量的一致性高，表明群体的意见收敛，故可用一致性来表征群体意见的收敛程度。任选两个专家Va、Vb，他们之间的一致性可表示为：

其中k={kj|j=1，2…n}表示方案的属性权重。

通过式（12）计算出群偏好矢量GV，则群体的一致性可表示为：

修正的关键就是优化上式中的k值，通过逐步修正使得群体的一致性提高，群体意见更加收敛。

1）当y＜0.5，∂f（x，y）/∂x＞0，f（x，y）随着x的增加而增加，函数取到极小值的条件是x→0；

2）当y＞0.5，∂f（x，y）/∂x＞0，f（x，y）随着x的增加而减少，函数取到极小值的条件是x→1。

根据这个函数的性质，结合聚类的思想，构造如下函数表达式：

通过这种一致性偏离0.5的方法能够有效地优化成员的聚类效果，从而提高群体的一致性。

通过上述分析，建立的偏好一致性修正模型如下：

2.3 模型求解

对比式（16）、式（7），可以发现本节的一致性修正模型与前一节优化模型属于同一性质的带约束优化问题，因此，本模型求解可以参考前一节的求解过程，依旧采用花朵授粉算法。所不同的是，将前一节寻求目标函数的最大值改为求解本节目标函数的最小值即可。同时目标函数不需要达到最小值，只需达到决策者满意的某一阈值即可。

2.4 方案排序

通过计算出专家的权重以及方案属性权重，可计算出每个方案的值：

通过比较各个方案最终值的大小即可对方案进行排序。

3 实例分析

假设有10个专家针对3个方案进行择优排序，每个方案有5个评判属性，专家针对每个方案给定的属性偏好值如表1～表3所示。

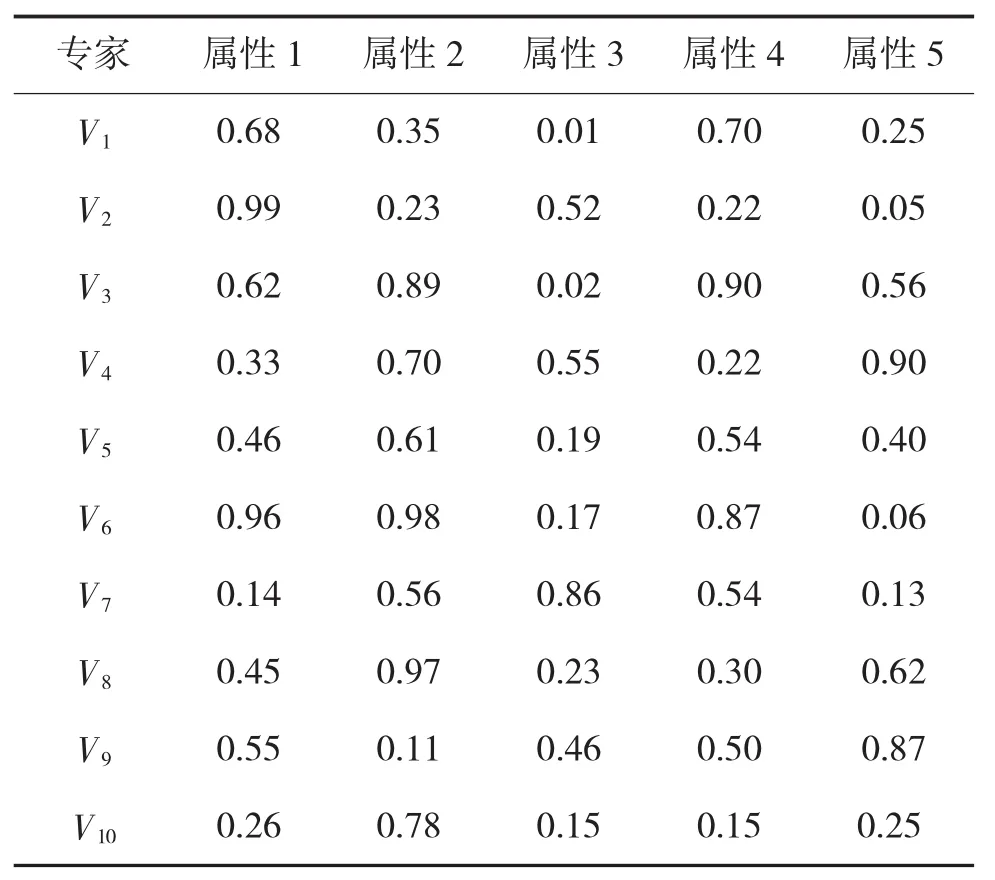
表1 方案A的专家偏好矢量表

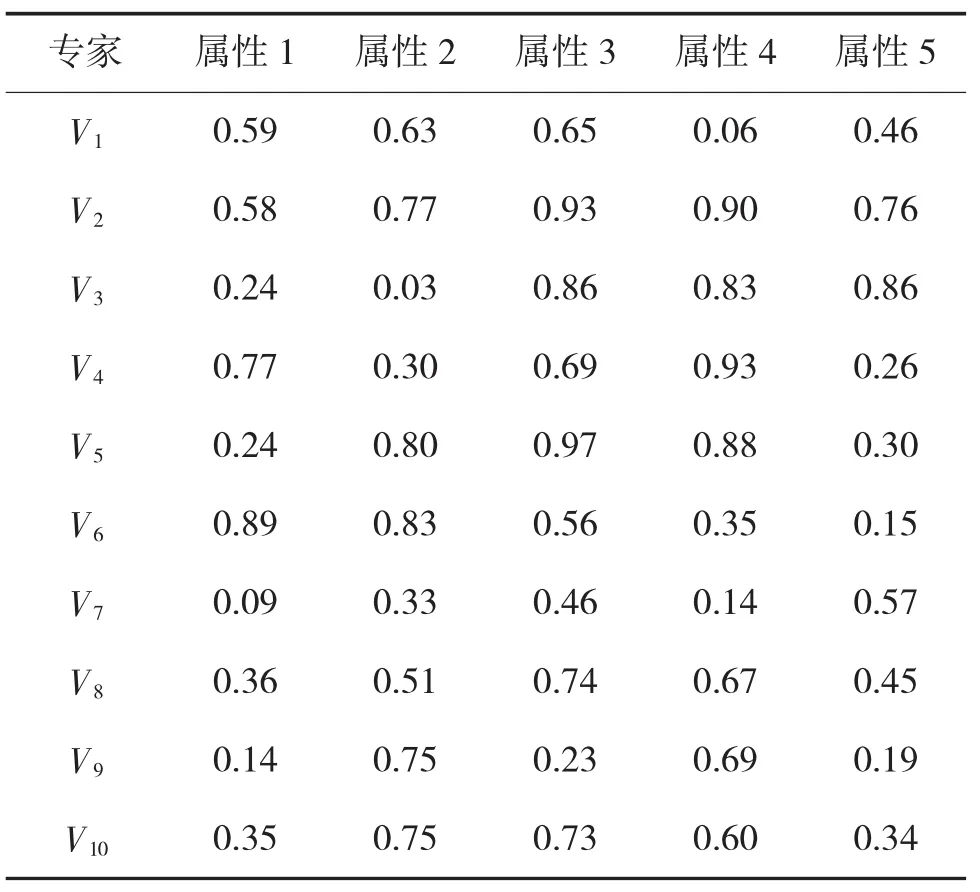
表2 方案B的专家偏好矢量表

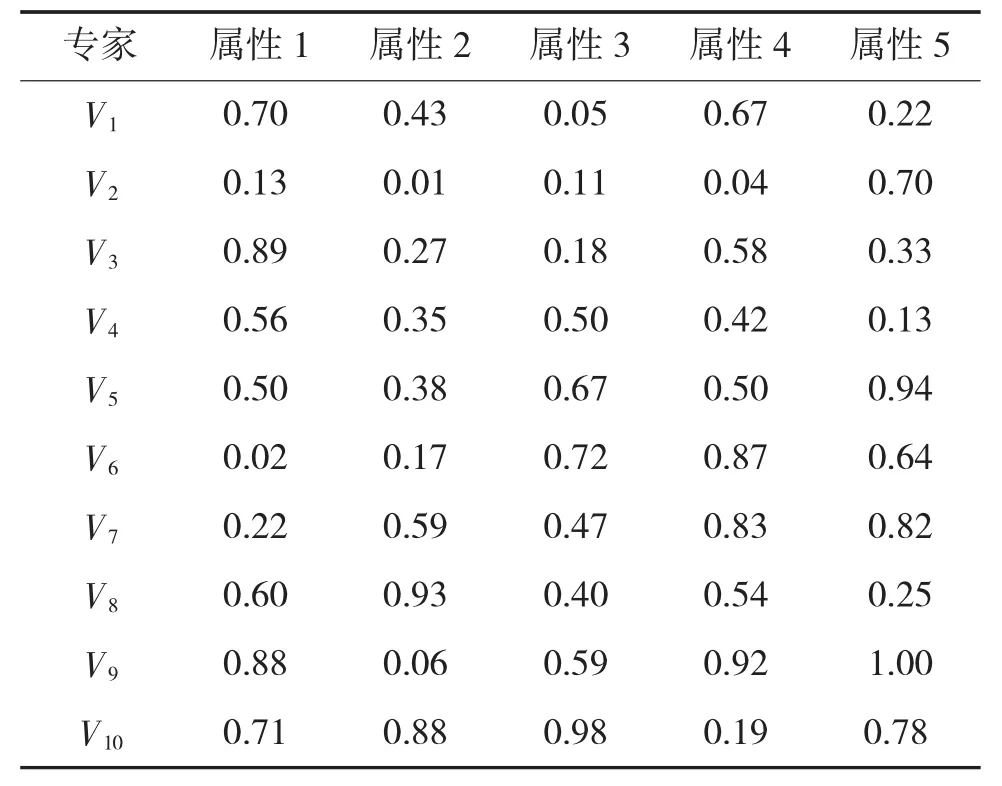
表3 方案C的专家偏好矢量表

Step1：通过花粉算法求解专家权重优化模型，带入数据，θ=0.5，结果如图1所示。

得到的专家权重矢量为：w=（0.096 1，0.101 3，0.105 3，0.095 8，0.098 6，0.114 3，0.098 5，0.094 9，0.101 1，0.094 2）；

Step2：通过式（8）求得群体偏好矢量，如表4所示。

Step3：假设决策者设定的阈值为两次F（v）的差值小于0.000 1时，迭代过程结束。通过花粉算法求解群体一致性修正模型，带入数据，结果如图2所示。得到最终属性权重 k=（0.107 0，0.186 1，0.236 6，0.107 0，0.363 3）；

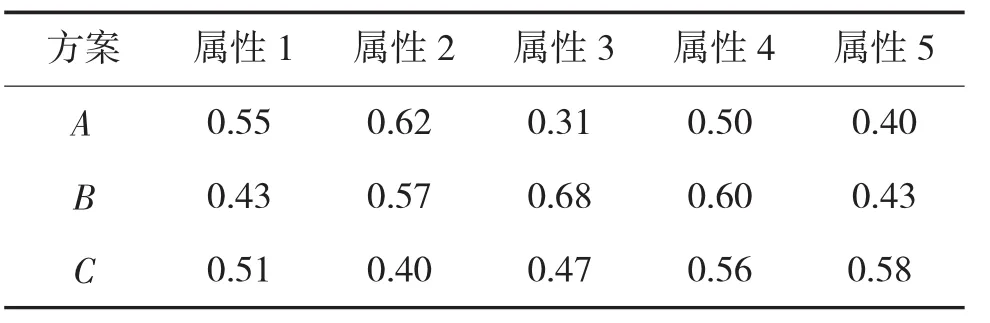
表4 群体偏好矢量表

Step4：通过式（17）得到各个方案的最终偏好值如表5所示。

比较偏好值得到3个方案的排序为：

表5 方案最终偏好值

4 结论

本文研究了多属性大群体决策中的方案排序问题，分别针对专家权重未知和群体一致性较低两个问题给出了相应的求解模型及算法，其中专家权重优化模型能够客观充分地从专家的偏好信息中挖掘出专家的权重，而群体一致性修正能够动态地对属性权重进行调整，专家能够不断优化自身偏好信息，能够较好地解决部分专家偏好差异性过大引起的一致性较差的问题。本文还针对专家数目较多的情况引用并改进了花粉算法，对模型进行了求解，并通过计算机仿真得到了结果。结果表明，本文的方法不仅理论上科学有效，而且具有可操作性。但本文的一致性修正模型适用的是属性权重经协商可调整的情况，对于某些属性权重不可变的决策问题则难以进行修正。

［1］谭吉玉.基于群体一致性的犹豫模糊多属性决策方法［J］.运筹与管理，2016，25（1）：105-109.

［2］胡浩，徐少华，宋继冉，等.基于直觉模糊动态信息交互的多属性群决策模型［J］.中南大学学报（自然科学版），2015，46（8）：2923-2929.

［3］张世涛.基于重要度引导偏好识别修正的多粒度语言共识模型［J］.控制与决策，2015，30（9）：1609-1616.

［4］郝晶晶.基于交互式修正的双重语言信息联动决策方法［J］.系统工程与电子技术，2014，36（5）：912-919.

［5］吴志彬，徐雷.两种基于个体偏好集结的多属性群决策共识方法［J］.控制与决策，2014，29（3）：487-493.

［6］程发新.基于共识决策的低碳供应商选择方法研究［J］.运筹与管理，2012，21（6）：68-73.

［7］杜元伟.基于思想的交互式多属性群决策方法［J］.系统工程学报，2011，26（1）：25-30.

［8］徐选华，范永峰.改进的蚁群聚类算法及在多属性大群体决策中的应用［J］.系统工程与电子技术，2011，33（2）：346-349.

［9］陈云翔.基于信息嫡的群组聚类组合赋权法［J］.中国管理科学，2015，23（6）：142-146.

［10］张宇，刘雨东，计钊.向量相似度测度方法［J］.声学技术，2009，28（4）：532-536.

［11］YANG X S.Flower pollination algorithm for global optimization ［C］//In：Unconventional Computation and Natural Computation，Lecture Notes in Computer Science，2012（7445）：240-249.

［12］YANG X S，MEHMET K，HE X S.Multi-objectiveflower algorithm for optimization［C］//International Conference on Computations Science，2013，18：861-868.

［13］SHARAWI M，EMARY E，SAROIT I A，et al.Flower pollination optimization algorithm for wireless sensor network lifetime global optimization［J］.International Journal of Soft Computing and Engineering，2014，4（3）：54-59.

［14］PRATHIBA R，MOSES M B，SAKTHIVEL S.Flower pollination algorithm applied for different economic load dispatch problems［J］.International Journal of Engineering and Technology，2014，6（2）：1009-1016.

［15］董振波.基于加权模糊聚类的不平衡数据分类方法［J］.现代计算机，2016，14（23）：25-27.

［16］王丽娟，吴成茂.基于样本属性加权的二维FCM聚类分割法［J］.计算机工程与设计，2016，37（6）：1604-1631.

［17］陈黎飞，郭躬德.属性加权的类属性数据非摸聚类［J］.软件学报，2013，24（11）：2628～2641.

［18］陈都，谭可可，安瑞楠，等.TOPSIS伪装决策方法在洞库工程中的应用研究［J］.兵器装备工程学报，2016，37（5）：77-80.

［19］BASAK J，DE R K，PAL S K.Unsupervised feature selection using a neuro-fuzzy approach［J］.Pattern Recognition Letters，1998，19（11）：997-1006.