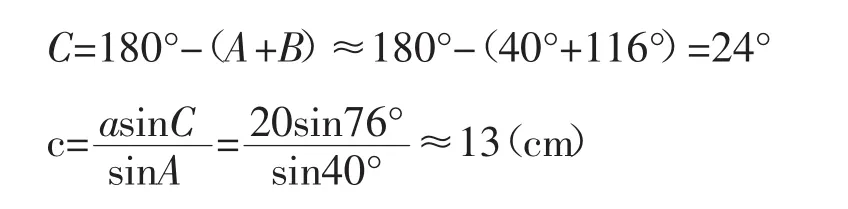解三角形中进一步的研究

柳 静

（六盘水市第一实验中学，贵州 六盘水）

一、已知三角形中的两个角和一条边，解三角形问题

在△ABC 中，A=α，B=β，c=c，解三角形。

解：∵A=α，B=β，∴C=π-α-β

二、已知三角形中的两个边以及两个边的夹角，解三角形问题

在△ABC中，已知a，b以及这两边的夹角C，解三角形。

三、已知三角形的三条边，解三角形

在△ABC 中，已知 a，b，c，解三角形。

四、已知两边及其中一边的对角

在△ABC中，已知a，b和A，解三角形。

解：分析已知a，b和A，我们先用正弦定理，计算出另一边的对角的正弦值并由此求出B；再用三角形内角和定理计算出第三个角C=π-A-B，然后，应用正弦定理计算第三边

1.如果已知的A是钝角或直角，那么必须a＞b才能有解，这时计算B时，只能取锐角的值，因此有一个解。

3.如果已知的A是锐角，并且a＜b，分三种情形来讨论。

例 在△ABC中，已知a=20cm，b=28cm，A=40°，解三角形（角度精确到1°，边长精确到1cm）。

解:根据正弦定理，

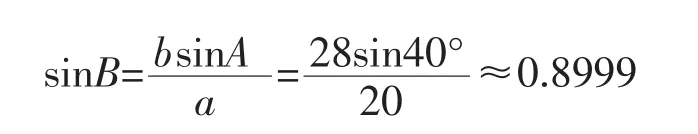
因为 0°＜B＜180°，所以 B≈64°，或 B≈116°

（1）当 B≈64°时

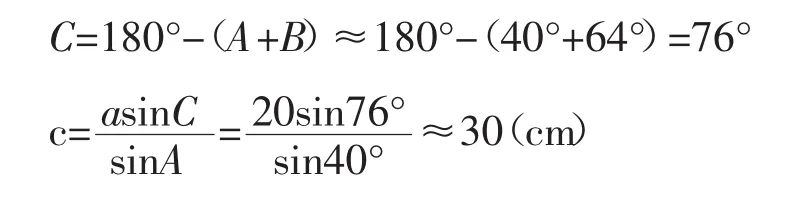
（2）当 B≈116°时