利用“L-R”剖分及三角形聚合的近似等面积菱形格网建模

苑争一，赵学胜，赵 静

(1. 中国地震台网中心，北京 100045； 2. 中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

全球离散格网(discrete global grid,DGG)是一种基于球面或椭球面的可以无限细分的地球拟合格网，该模型可以有效克服传统地图投影的束缚，从根本上解决传统平面格网模型在全球多尺度空间数据管理上的数据断裂、几何变形和拓扑不一致等问题[1-2]，为解决越来越多全球一体化背景下的宏观应用问题提供思路[3-4]。球面菱形格网因其几何结构简单，而且具有有一致的方向性、径向对称性及平移相和性，因而在空间操作和数据集成方面有着广泛的应用。文献[5]基于球面菱形格网模型，发展了具有固定方向的“块”层次编码技术及邻近搜索算法；文献[4]实现了在球面菱形格网上集成和管理中国海潮波系统模型相关数据；文献[6]提出了一种基于菱形格网的，用于层级间数据集中与分散的预测模型(Kalman过滤模型)。

格网等积性作为提高空间统计分析精度和空间采样合理性的有效手段[7]，已经成为球面格网模型构建的研究热点之一。目前的菱形剖分通常以球面三角剖分为基础，通过合并相邻的格网单元生成。传统的等面积球面三角剖分模型大多基于等面积投影，该类模型需要复杂的迭代计算，而且投影边界扭曲严重，为了方便球面点的定位，通常利用大圆弧线代替投影边界，而替代后的模型会引起格网单元的面积变形，如基于Snyder等面积多面体投影的ISEA剖分模型[8]。另外，Song等[9]提出了一种基于小圆弧的等面积剖分模型，该模型克服了投影法边界扭曲严重的缺陷，但其计算方式复杂，坐标转换困难；Seong[10]采用等长度的经线、纬线弧段构建了等积球面四边形格网，该方案破坏了格网单元间简洁的临近关系，增加了临近搜索的复杂性；Holhos等[11]针对传统投影方法计算复杂的缺陷，推导出了一种新的等面积投影公式，该公式具有对称性，计算简便，但是仍然没有解决传统投影方法边界扭曲严重的缺陷，而且球面点的定位较为复杂。文献[7]在Snyder等积投影的基础上，沿着面积误差率较大的3条轴线(由八面体中心到3个顶点)对相邻的球面三角形格网进行了两两合并，构建了一种近似等面积的球面菱形格网模型，该方法有效减小了格网单元的面积变形，但由于格网合并的方向不同，增加了模型构建的复杂性。文献[12]提出了一种计算简便，同时又具有层次嵌套性、格网统一性和全球无缝连续性等特点的近似等面积QTM剖分方法——纬线环法(latitude-ring (L-R) method)。

通过分析纬线环法QTM模型的格网单元面积变形规律，发现该剖分模型的格网单元面积变形具有锯齿分布特征，即相邻的上下两个格网单元总是一大一小交替分布，而且变形方向一致。因此，本文以该模型为基础，通过合并上下两个相邻的三角形单元，得到一种新的面积更加接近的球面菱形剖分模型，最后设计相关变形试验，分析该模型的格网单元面积变形特征及分布规律。

1 基于纬线环法的等面积QTM模型

文献[12]提出了一种基于纬线法QTM剖分及变经纬度剖分的近似等面积剖分方案——纬线环法QTM剖分，其基本思路为：通过相邻两条纬线所围成的纬线环的理想面积(该纬线环所包含的三角形个数与理想剖分单元面积的乘积)，构建方程依次求解每条分割纬线的位置，进而通过平分经度的方法确定格网间的经度间隔，完成对整个球面的QTM剖分(具体过程详见文献[12—13])。

按照传统的纬线法和上述纬线环法分别对球面进行了QTM剖分，同时计算了格网单元的面积变形率。以1/8球面为例，将球面剖分6层，把格网中心点投影到球面内接正八面体的一个面上，用Z轴表示格网单元的面积变形率，得到了图1所示的两种剖分模型的格网单元面积变形率的对比图。从中可以看出，“L-R”QTM剖分(图1①部分)除了极点附近外的其他大部分区域都非常接近于理想QTM(图1③部分，其格网单元无面积变形)，表明该剖分有效控制了格网单元的面积变形，能够达到近似等面积剖分的效果。

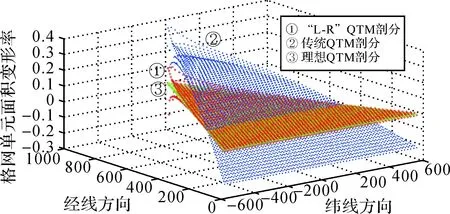
图1 两种剖分方法的面积变形对比(第6层)

为了进一步研究该模型面积变形的空间分布情况，分别计算每个格网单元的面积，根据其大小赋予不同的灰度值，借助DirectX绘制在球面上得到了第4—6层的QTM格网单元面积分布灰度图和面积分布直方图，如图2所示。从中可以看出：①格网单元面积变形分布呈现出规则的锯齿状特性，即相邻两个格网单元的面积总是一大一小的交替分布，该变形特征便于沿同一方向进行三角形聚合；②尽管由大圆弧线代替投影曲线产生了面积变形，但观察面积变形分布直方图可以发现，格网单元面积分布较为集中，即格网单元的面积近似性较好。综上所述，纬线环法QTM剖分不但能够有效控制剖分单元的面积变形，而且其不需要复杂的投影及迭代计算，可以大大提高剖分的效率。因此，本研究拟在此剖分方法的基础上，通过三角形聚合的方法实现对球面的菱形剖分。

2 球面菱形格网剖分及变形分析

2.1 剖分过程

菱形格网生成的详细过程如图3所示。首先按上一节中的纬线环法对八分之一球面进行近似等面积剖分；进而通过旋转实现对整个球面的QTM剖分；将球面沿0°、90°、180°、270°经线展开成4个基础菱形块；最后在每个基础菱形块中合并相邻的上下两个三角形格网单元，从而得到覆盖整个球面的菱形剖分。

2.2 格网单元面积变形分析

按上述方法构建了球面菱形剖分模型，计算出了每个菱形格网面积变形率(相对于理想剖分)。为了便于比较聚合前后格网单元面积变形情况的差异，同时计算了基础QTM剖分的格网单元面积变形率。本节将从格网单元面积变形分布区段及格网单元面积变形位置分布两个方面出发，对比分析剖分模型聚合前后的面积变形情况。

2.2.1 剖分单元面积变形分布区段研究

根据式(1)计算格网单元相对于理想剖分单元的面积变形率(Area_dis_rate)，式中：area为剖分单元面积；areanorm为理想剖分单元面积。

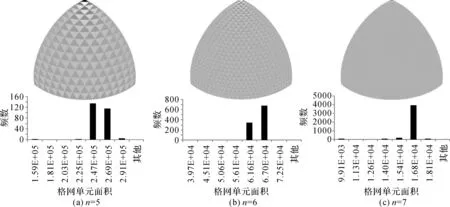
图2 格网单元面积分布灰度图、面积分布直方图

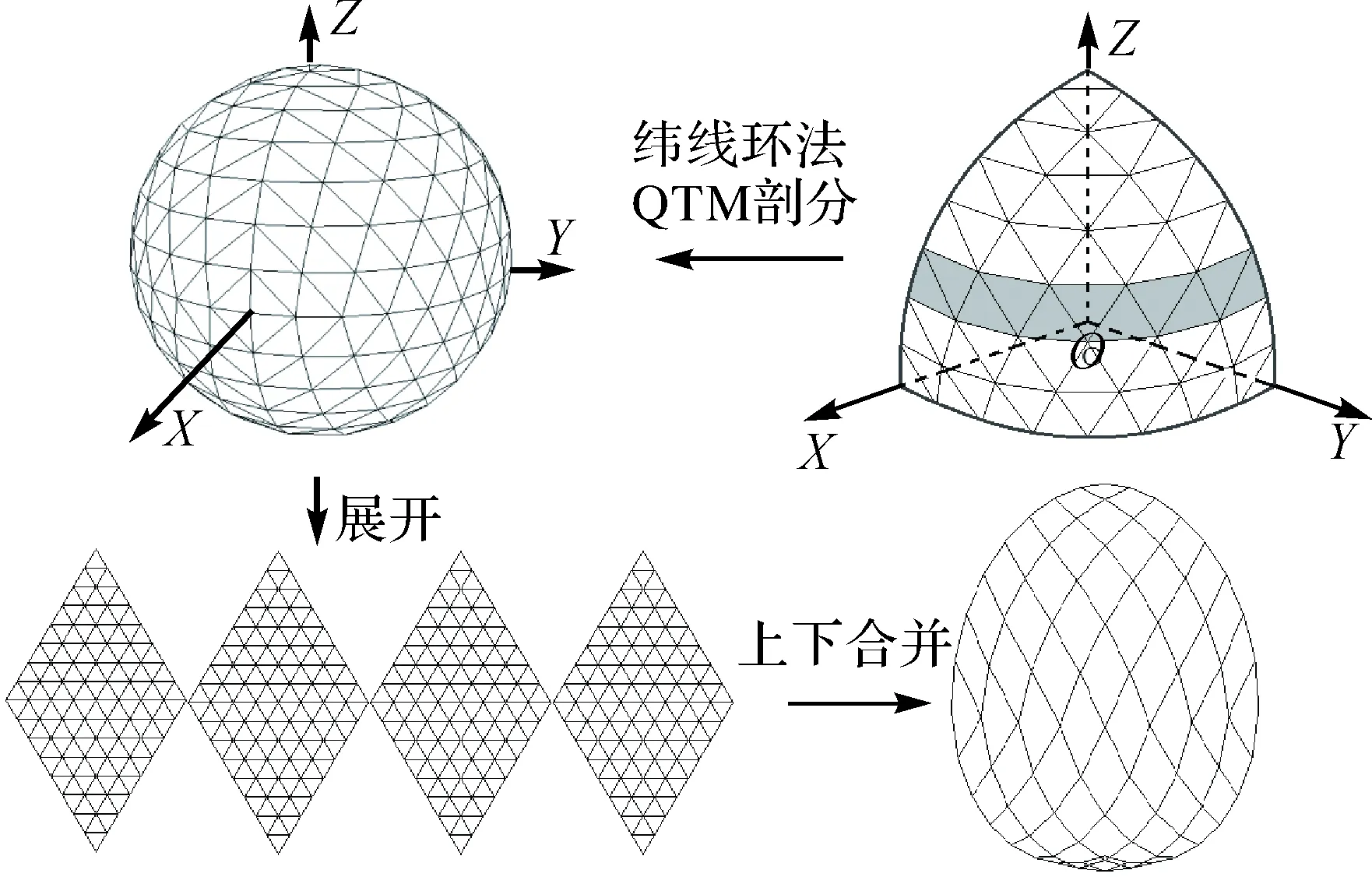
图3 菱形格网生成过程

(1)

基础QTM剖分的格网单元面积变形率分布区段见表1，从中可以看出：基础三角剖分模型在前5层中面积变形率的分布无明显的规律，第6层以后格网单元面积变形率分布近似呈正态分布(如图4所示)。随着剖分层次的增加，模型的面积变形情况继续改善，第8层以后剖分单元面积变形率被控制在±1%以内的格网单元达到99%以上。

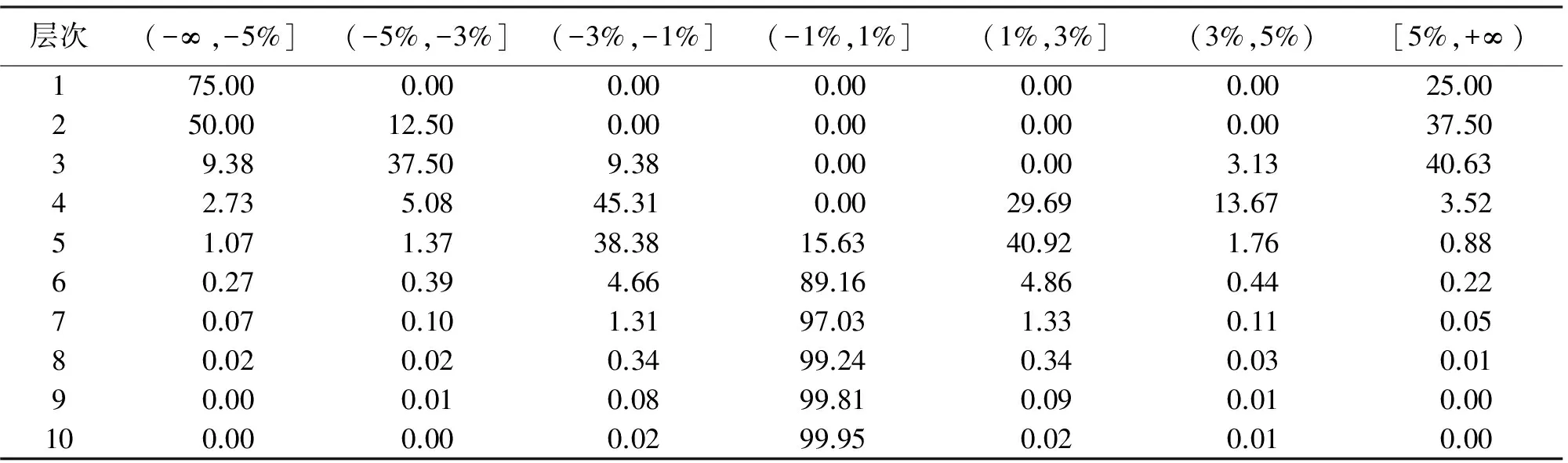
表1 基础三角剖分单元面积变形率分布区段 (%)

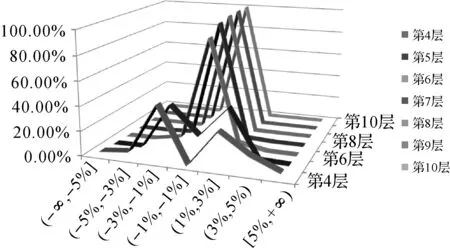
图4 纬线环法QTM剖分面积变形的统计特征

聚合菱形剖分单元面积变形分布区段见表2，可以看出：聚合菱形剖分模型在前3层中面积变形率的分布无明显规律，第4层以后90%以上的格网单元面积变形率分布在±1%以内；将面积变形区段(-1%，1%]进一步细分，并统计了剖分单元的面积变形率在第6～10层的分布情况，从中可以看出：格网单元面积变形情况继续得到改善，第8层以后面积变形率被控制在±0.1%内的格网达到99%以上。

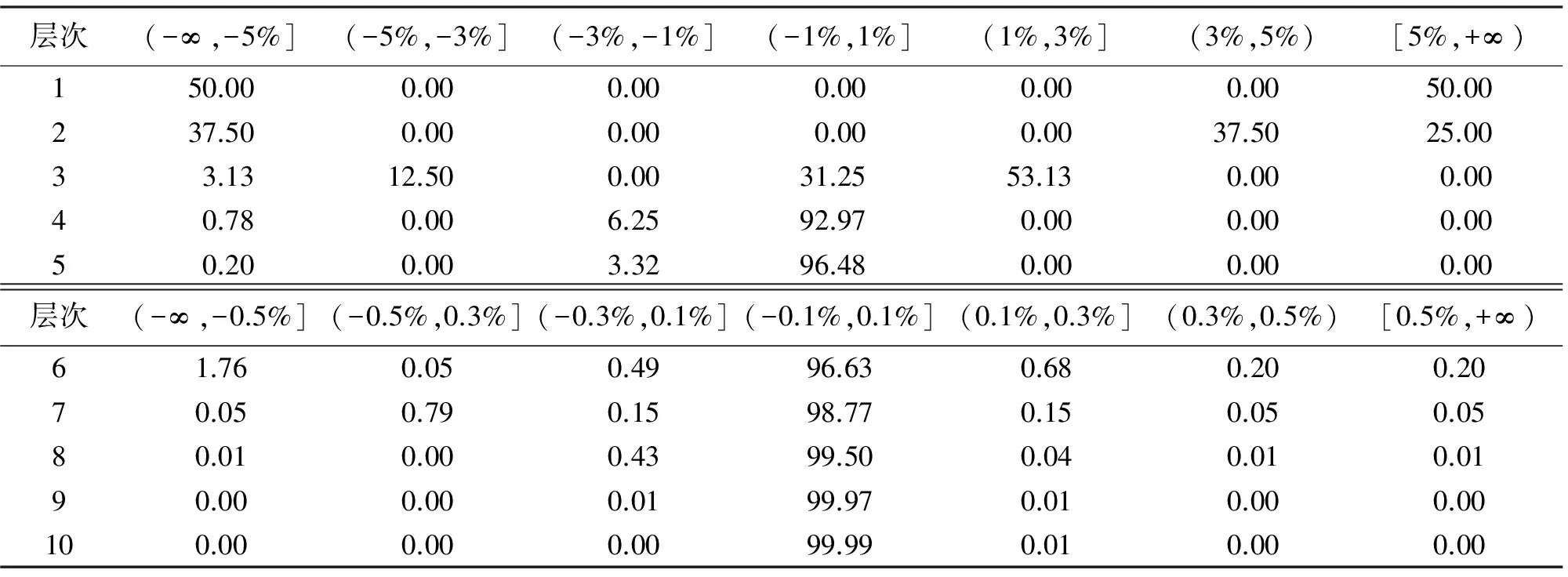
表2 聚合菱形剖分单元面积变形率分布区段 (%)

2.2.2 剖分单元面积变形位置分布研究

以八分之一球面和对应的聚合后的一个菱形块为例，将球面剖分4、5、6层，给每个面积变形率分布区段对应一个特定的灰度值，借助DirectX绘制了剖分模型面积变形率的位置分布灰度图(如图5、图6所示)。图中浅色区域的格网单元面积变形率较小，深色区域较大。

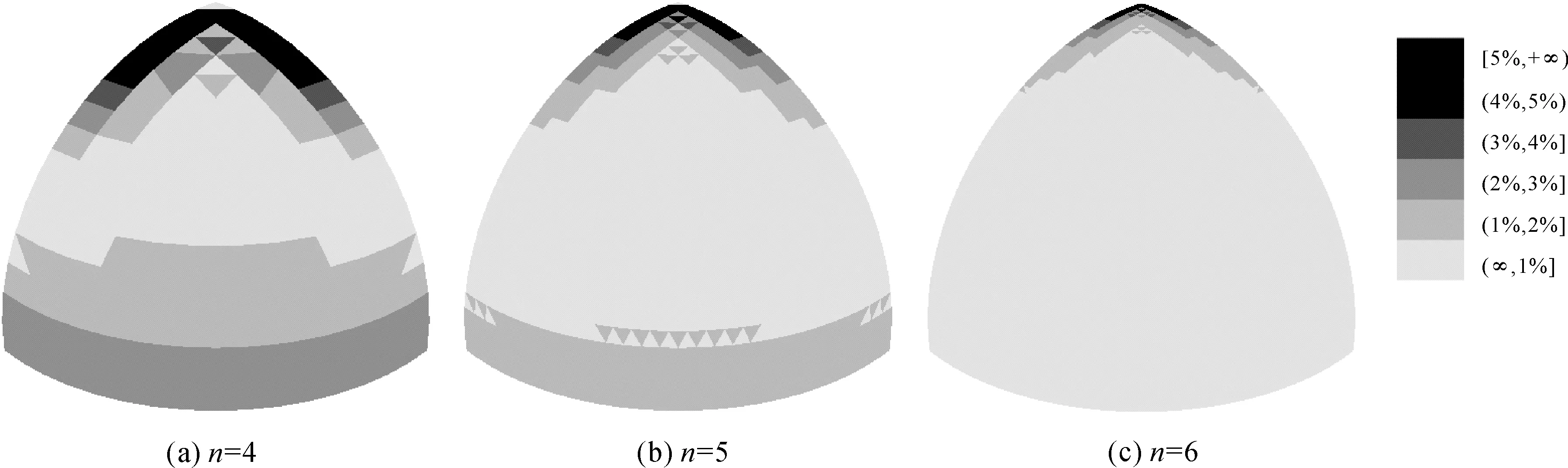
图5 基础QTM剖分格网单元面积变形率的位置分布

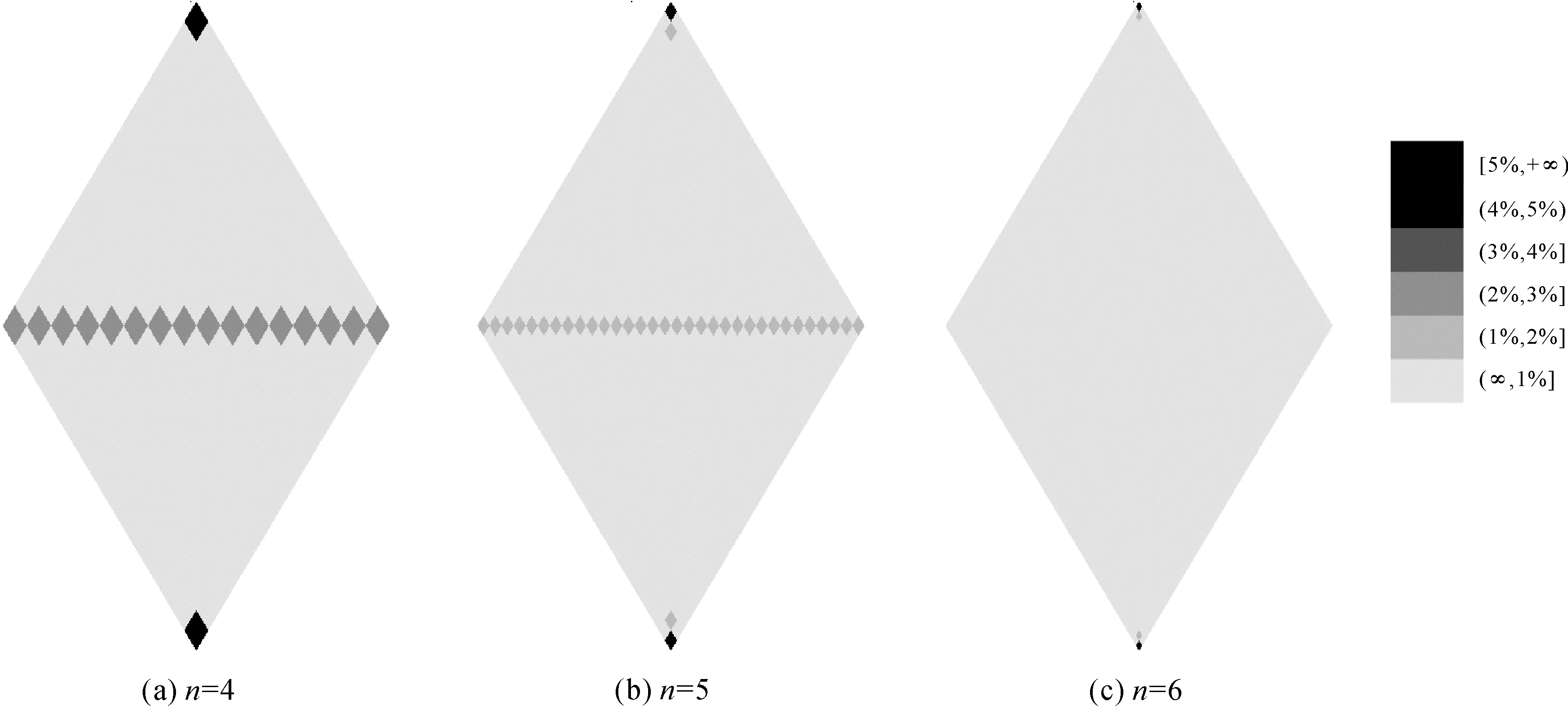
图6 聚合菱形剖分单元面积变形率的位置分布

从图6及其层次变化可以看出：①随着剖分层次的增加，三角剖分模型的面积变形情况逐渐得到改善，变形边界(变形率=1%)逐渐向极点移动；②随着剖分层次的增加，聚合菱形剖分模型的面积变形情况也不断改善，第6层以后，中低纬度绝大部分区域的面积变形被控制在1%以内；③对于相同层次的两种剖分模型，聚合菱形剖分模型的面积变形率更小，分布也更加均匀。

3 结 语

本文利用纬线环法QTM剖分方法，构建了近似等面积的球面四元三角剖分模型，并分析了该剖分模型的格网单元面积变形。在此基础上通过三角形聚合，构建了一种面积近似效果很好的球面菱形剖分模型。通过对比聚合前后的格网单元面积变形情况，得出了以下结论：

(1) 面积变形小：聚合前的三角形剖分模型，其相邻的上下两个格网单元总是一大一小交替分布，通过将其聚合成菱形格网后，有效地减小了这一变形。相比同层次的三角剖分，聚合菱形剖分模型的格网单元面积变形率更小。

(2) 位置分布明确：不论是基础三角剖分，还是聚合后的菱形剖分，其面积变形都会随剖分层次的增加而不断改善，中低纬度区域不断接近等面积剖分。相比之下，聚合菱形剖分的改善效果更好，第6层以后，除了极点处的极少数格网单元，其他区域基本达到了近似等面积剖分的效果，能够满足绝大部分统计分析的应用需求。

另外，由于该剖分方案不涉及复杂的投影变换和迭代计算，显著加快了计算速度，从而有效提高了剖分的效率。

[1] 赵学胜，王磊，王洪斌，等.全球离散格网的建模方法及基本问题[J].地理与地理信息科学,2012, 28(1)：29-34.

[2] 赵学胜，侯妙乐，白建军.全球离散格网的空间数字建模[M].北京：测绘出版社,2007.

[3] 邢华桥，侯妙乐，王磊，等.基于QTM的大范围有源淹没算法研究[J].测绘通报,2015(12)：46-49.

[4] 刘光鑫.基于菱形离散格网的中国海潮波系统数据集成方法[D].赣州：江西理工大学,2013.

[5] 赵学胜，白建军.基于菱形块的全球离散格网层次建模[J].中国矿业大学学报,2007, 36(3)：397-401.

[6] HUANG H, GRESSIE N. Multiscale Spatial Modeling[C]∥Proceeding of the Section on Statistics and Environment.[S.l.]：IEEE,1997.

[7] 孙文彬，周长江.一种近似等面积球面菱形格网的构建方法[J].武汉大学学报(信息科学版),2016, 41(8)：1040-1045.

[8] SNYDER J P. An Equal-area Map Projection for Polyhedral Globes[J]. Cartographica: The International Journal for Geographic Information and Geovisualization,1992, 29(1)：10-21.

[9] SONG L, KIMERLING A J, SAHR K. Developing an Equal Area Global Grid by Small Circle Subdivision[C]∥Second International Conference on Discrete Global Grids. Santa Barbara: National Center for Geographic Information & Analysis, 2002.

[10] SEONG J C. Implementation of an Equal-area Gridding Method for Global-scale Image Archiving[J]. Photogram-metric Engineering& Remote Sensing,2003, 71(5)：623-627.

[12] 赵学胜，苑争一，赵龙飞，等.一种改进的近似等面积QTM剖分模型[J].测绘学报,2016, 45(1)：112-118.

[13] 赵学胜，孙文彬，陈军.基于QTM的全球离散格网变形分布及收敛分析[J].中国矿业大学学报,2005, 34(4)：438-442.

[14] GOODCHILD M F. Criteria for Evaluation of Global Grid Models for Environmental Monitoring and Analysis[J]. Handout from NCGIA Initiative,1994, 15：9-47.

[15] ZHOU L C, LIN B X, LV G N, et al. Distortion Distribution and Convergence Analysis of Spherical Diamond Discrete Grids[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences,2013, 1(2)：89-93.

[16] 孙文彬，赵学胜，高彦丽，等.球面似均匀格网的剖分方法及特征分析[J].地理与地理信息科学,2009, 25(1)：53-56.