GNSS自动化监测系统的大坝变形预测方法研究

2018-02-28陈渠森鞠博晓

测绘通报 2018年1期

黄凯，陈渠森，鞠博晓

(1. 武汉大学卫星导航定位技术研究中心，湖北武汉 430079； 2. 武汉大学测绘学院，湖北武汉 430079)

全球导航卫星系统(global navigation satellite system，GNSS)定位技术近年来以其全天候、高精度、自动化等优点，在高精度大坝变形监测领域得以广泛应用。由于大坝变形具有连续、缓慢、量级小等特点，一般在大坝关键结构上布设固定连续的静态GNSS监测阵列，采取几十分钟到数小时时段的静态解算进行数据处理[1]。自动化的GNSS监测系统为大坝运行状态监测、变形规律研究提供了大样本、高采样率、连续的大坝变形资料，对其进行合理的分析，建立科学的变形分析与预报模型，对大坝安全运营具有重要意义。

目前，大坝变形预报一般考虑水位、温度、时效等因素，建立统计模型、确定性模型和混合模型。然而，GNSS自动化监测数据具有大样本、高采样率的特点，常用的有限元单元法存在参数确定困难，计算复杂等问题；灰色理论、支持向量机法在小样本的变形预测中效果良好，但不适用于大样本情境；多元回归分析等方法也无法准确表达大坝变形与环境量间复杂的非线性关系；利用自身过去到现在的大坝变形观测值建立的自回归模型，由于随机因素的影响，也存在外延预报时间短、精度低等缺陷[2-7]。

针对上述难题，本文提出了一种结合小波分析与BP、NAR神经网络预测大坝变形的新方法。该方法利用了长时间连续的GNSS变形监测资料中蕴含的长期非线性趋势与不同尺度的周期波动特征，充分挖掘了大坝变形中隐藏的内在规律，经实例分析，与单一BP神经网络、NAR神经网络方法相比，该方法预测精度更高、泛化性能好，在采用GNSS自动化监测系统的大坝变形预测中具有推广应用价值。

1 预测原理与方法

1.1 BP神经网络基本原理

BP(back propagation)神经网络是一种按误差反向传播算法训练的多层前馈神经网络。它具有极强的非线性映射能力。理论上，一个3层或3层以上的BP神经网络能够以任意精度逼近一个非线性函数，是目前应用最广泛的神经网络模型之一[8]。

已有研究表明，标准的BP算法存在着易陷入局部极值、收敛速度慢、过度训练等问题[9]。为了提升网络的泛化能力和训练性能，本文采用贝叶斯正则化算法作为神经网络的训练函数。BP神经网络一般采用均方误差(MSE)作为网络性能函数，而采用正则化算法将网络性能函数修正为

F=βED+αEW

(1)

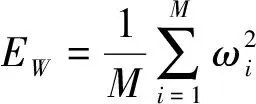
一般的正则化算法难以确定α和β的大小，当α≤β时，训练算法尽可能减小网络误差，容易导致过拟合；当α≥β时，训练算法尽可能减少有效的网络参数，提升网络泛化性能，容易导致欠拟合。贝叶斯正则化算法将神经网络连接权值视为随机变量，认为训练集和网络连接权集的先验概率服从高斯分布，依据贝叶斯准则，由后验概率最大化求解目标函数E的α和β值，从而在网络训练过程中自适应地调整α和β的大小，在确保网络误差平方和最小的前提下，有效控制网络规模复杂度，从而显著提高BP神经网络的泛化能力[10]。

1.2 NAR神经网络基本原理

NAR(nonlinear autoregressive)神经网络属于动态神经网络,NAR神经网络定义为[11-12]

y(t)=f(y(t-1),y(t-2),…,y(t-d))

(2)

式中，y(t)为当前时刻输出值；y(t-1),y(t-2),…,y(t-d)为历史时刻输出值；d为延迟阶数。

NAR神经网络由输出层、隐层、输出层及输入延迟阶数组成。其神经网络结构如图1所示。

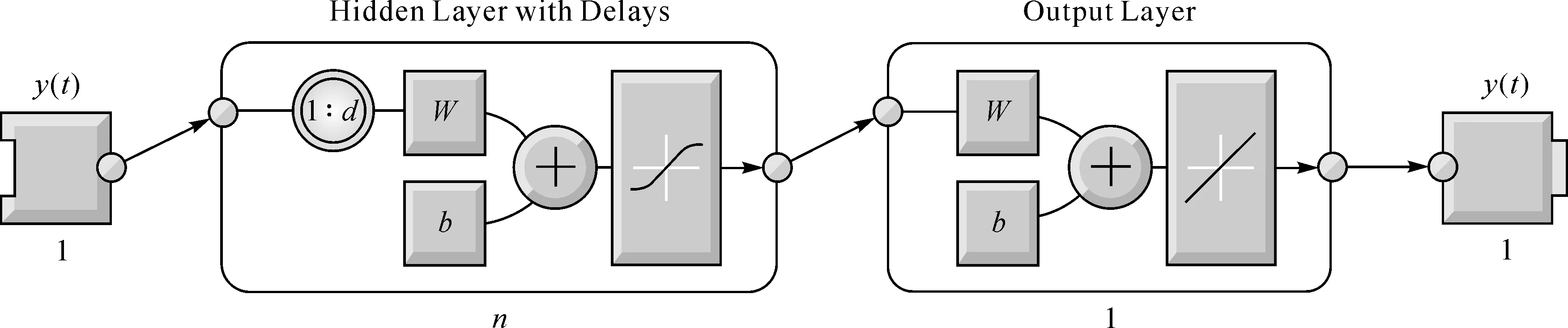
图1 NAR神经网络结构

图中，y(t)表示神经网络的输出；d为延迟阶数；n为隐层神经元个数；W为权值；b为阈值。

NAR神经网络基于自回归原理，利用前期若干时刻的自身历史值来推断当前时刻的输出值。相比于静态多层前馈型网络，NAR神经网络具备反馈和记忆功能。在网络学习训练过程中采用串联模式(Openloop)，网络转变为静态的前向神经网络，用真实的输出代替预测反馈值进行网络训练。预测过程中采用并联模式(Closeloop)，每一次预测的输出反馈到输入端，作为下一次输出的调整参数，完成对神经网络的调整，循环使用多次一步向前预测，实现NAR神经网络的多步预测。为了提升神经网络的泛化能力，本文采用贝叶斯正则化算法作为NAR神经网络训练函数。

1.3 基于多尺度小波分析与BP、NAR神经网络的预测模型

GNSS大坝变形数据序列具有较明显的多尺度特征，利用多尺度的小波分析可将大坝变形序列分解为不同尺度的低频信号和高频信号[13-14]。设GNSS大坝变形序列为X(t)，对该序列进行小波分解，假设分解级数为j，可得到位移序列从低频到高频不同尺度的信息。再对分解后的各分量序列分别进行小波重构，得到

(3)

式中，Aj(t)为近似序列；Di(t),i=1,2，…,j为不同尺度下的细节序列。

基于BP神经网络优秀的非线性映射能力，采用BP神经网络拟合低频近似序列，并预测其长期变形趋势；采用NAR神经网络对不同尺度下的高频细节序列进行建模，预测其不同尺度的周期性波动。叠加各尺度下预测结果，获得大坝变形预测值。预测模型结构如图2所示。

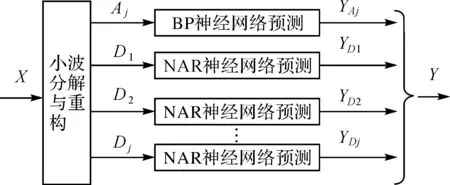
图2 预测模型结构

2 工程实例分析

本文以西龙池上水库GNSS大坝变形监测系统为例，选取水库主坝体L022号GNSS监测点与坝轴线垂直的水平方向变形观测序列进行建模，监测时间从2012年3月到2014年2月底，数据解算时段为4 h，共4380期数据，预测未来15 d(共90期)变形数据，并与实测数据进行比较来验证本文预测模型的有效性及精度。

受极端天气、设备故障等因素影响，变形监测数据一般存在缺失值。由于大坝变形序列非线性特征明显，当连续缺失值数量较多，传统的曲线拟合法插值效果差。本文采用BP神经网络拟合大坝变形时间序列，利用缺失数据时间段的神经网络预测值完成非线性插值。经过预处理后，对大坝变形序列进行小波信号分解，小波的分解级数应根据具体情况恰当选择。本文经过实验比较后，选择采用sym8小波对大坝变形序列进行6层分解，分解后的各个分量如图3所示。

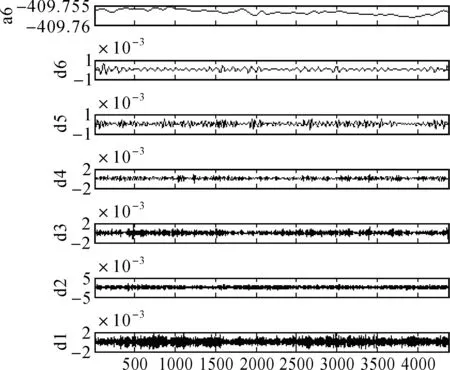
图3 原始观测序列及各个分解分量

由图3可看出，低频近似序列a6整体较为稳定，为了研究近似序列的非线性变化特征，本文采用BP神经网络拟合该序列，经试验比较分析，神经网络设计为双隐层，每层10个神经网络元；不同尺度下的高频细节序列存在明显周期性波动，长时间的连续观测序列为研究不同尺度下周期性波动特性提供了丰富的研究资料，故本文采用NAR动态神经网络对各尺度下的细节序列进行建模，经试验比较分析，神经网络的延迟阶数定为24，神经网络设计为双隐层，每层5个神经网络元。为了降低建模误差，神经网络训练前，将各分量数据归一到[-1,1]区间，预测后反归一化为真实预测值。各分量预测结果如图4所示。

图4 各分量预测值(实线：预测值；点：实测值)

由图4可看出，近似序列a6的BP神经网络预测效果较好，并预测误差随预测时间逐渐增大。不同尺度下各细节序列的预测效果受神经网络训练样本的规律性与预测时段外部因素变化共同影响，d6、d5、d4序列的NAR神经网络预测误差随时间逐渐增大，d3、d2中期预测误差增大后，整体预测效果仍然不错。由于GNSS大坝变形序列受明显的周日信号影响，量级约1 mm。该信号受GNSS卫星星座几何分布、多路径效应、基准站观测墩热胀冷缩等多种因素影响，规律复杂，故d1序列在初始的几期预测精度较高，之后迅速下降。

为了评价本文预测方法的整体预测效果，分别选用单一BP神经网络拟合、单一NAR神经网络与本文预测模型的预测结果进行比较，评价指标采用均方根误差(RMSE)和平均绝对误差(MAE)。不同预测方法的预测结果见表1。

由表1可以看出，本文提出的预测方法在不同预测期数下的预测精度都明显高于单一BP神经网络和NAR神经网络模型。

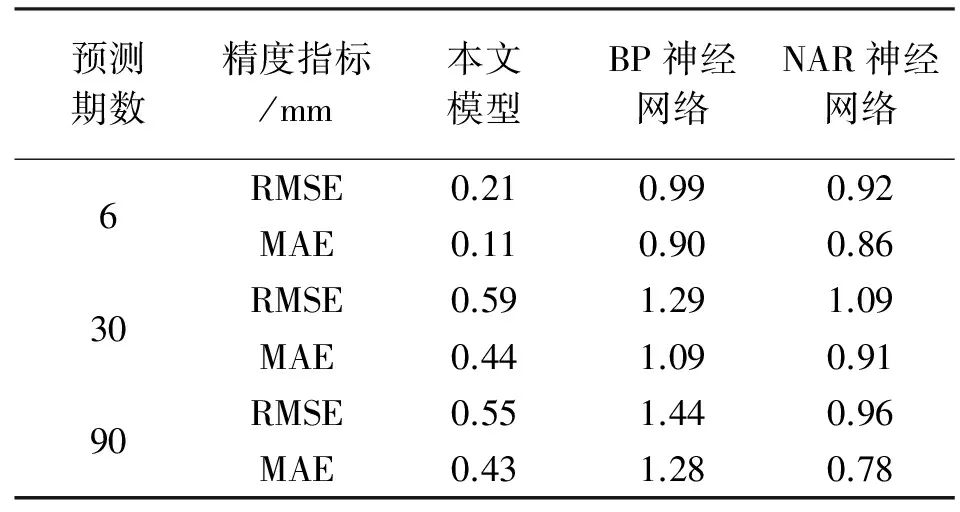
表1 不同预测方法的预测结果

工程实例表明，在高采样率的观测下，大坝变形受诸多因素影响，成因复杂，难以摸清规律。然而GNSS自动化监测系统长时间、大样本的历史观测数据为探究大坝变形内在规律提供了突破口。通过多尺度的小波分析可分离出大坝变形中的长期非线性变化趋势与不同尺度的复杂周期波动特征；利用BP神经网络对反映长期变化趋势的低频近似序列的建模分析，可有效预测变形的整体趋势；利用NAR动态神经网络对反映周期性波动特征的不同尺度的细节序列建模分析，可有效预测变形中规律的周期性波动趋势。通过试验对比分析，与采用BP神经网络对整体变形序列建模分析和采用NAR动态神经网络对序列自回归特征建模分析相比，本文预测方法兼顾了长期的历史数据内在规律挖掘与短期的随机扰动影响，取得了更加优越的预测效果。

3 结语

随着GNSS自动化监测系统在大坝、滑坡、桥梁等领域的广泛应用，基于大数据的分析工作也日益受到关注。本文针对采用GNSS自动化监测系统的大坝变形预报问题，提出了一种结合小波分析与BP、NAR神经网络预测大坝变形的新方法。经对比试验表明，该方法具有很高的预测精度和良好的泛化能力，在采用GNSS自动化监测系统的大坝变形预测中具有推广应用价值。

[1] 姜卫平，刘鸿飞，刘万科,等.西龙池上水库GPS变形监测系统研究及实现[J].武汉大学学(报信息科学版)，2012，37(8):949-952.

[2] 张贵钢.三门峡大坝变形监测的有限元分析及预测[D].西安：长安大学，2007.

[3] 张永光，王兰锋，吕开云.小浪底水利枢纽大坝变形的灰色预测模型[J].测绘科学，2006，31(6):80-81.

[4] 王新洲，范千，许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报(信息科学版)，2008，33(5):469-471.

[5] 李潇.灰色最小二乘支持向量机在滑坡变形预测中的应用[J].测绘通报，2010(6):44-46.

[6] 覃劭峰.基于GM(1,1)-ARIMA最优组合的大坝预测模型[J].测绘通报，2014(S2):66-69.

[7] 范千,王新洲,许承权.大坝变形预测的支持向量机模型[J].测绘工程,2007,16(6):1-4.

[8] 朱大奇，史慧.人工神经网络原理及应用[M].北京：科学出版社，2006.

[9] 陈孝趋，鲁聪达，廖枝平.BP算法的改进及其在Matlab上的实现[J].控制工程，2005(S1):100-102.

[10] 李旭军.贝叶斯正则化的BP神经网络在经济预测中的应用[J].科技信息(学术版)，2008(4):73-75.

[11] 岳新征，李磊民，孙飞.基于NAR动态神经网络的石英挠性加速度表参数建模与预测[J].西南科技大学学报，2016，31(1):88-92.

[12] 葛宇生.基于NAR动态神经网络后验信息的概率水文预报[D].哈尔滨：东北农业大学，2016.